Abstract
The near-bit strap-down measurement-while-drilling (MWD) system has been developed in this paper. By means of triaxial magnetometers, calculation method for bit rotational velocity was developed to monitor the drill bit torsional vibration. A number of techniques were applied to perform a nonlinear analysis of the experimental data of torsional vibration. Estimate delay time with mutual information and calculated the embedding dimension through Cao’s method, after reconstruct the phase space, the chaotic characteristics of the system were analyzed by calculating the correlation dimension and the largest Lyapunov exponent. We show that the largest Lyapunov exponent is positive and the correlation dimension is more than two, which is a strong indicator for the chaotic behaviour of the system. We also found that chaotic characteristics of the drill bit torsional vibration even existed in the whole drilling process, and thus the techniques based on phase space dynamics can be used to analyze and to predict drill bit torsional vibration. The results of this paper are of interest to applied and theoretical mechanics and petroleum engineering.
1. Introduction
In oil and gas drilling engineering, the drill bit is powered to rotate with drill string by surface equipment to break rocks. During a stationary period, the rotation speed of drill string provided by the surface power system is invariable. However, due to the affection of formation rocks, the rotation speed of the drilling bit is in constant changing. This is so called drill string torsional vibration phenomenon. The lower part of the drill string comprised of drill-collars, stabilizers, measurement while drilling (MWD) systems and the drill bit is called the bottom-hole assembly (BHA). The dynamic behavior of the BHA is greatly responsible for the most harmful vibrations, represented by the torsional, axial and lateral modes and the coupling mechanisms between them.
Drill string torsional vibration in the drilling process caused widespread concern after it’s discovered because of its great dangers and inevitability. As early as 1968, Cunningham first proposed drillstring rotation speed inhomogeneity by analyzing down-hole measurement data [1], but that time did not attract enough attention. In 1982, Belokobyl’skii and Prokopov attributed to this vibration for the self-excited, account that the phenomenon of torsional vibration is caused by the nonlinear friction of the negative damping generated on the rupture surface when the drill bit broken rock, open the drill string torsional vibration mechanism research [2]. Many researchers concluded by a large number of theoretical models and experimental data that drillstring self-excited vibration caused by the drill negative damping torque [3, 4], and the nonlinear friction between the drill string and the borehole wall is formed reasons lead to drill string torsional vibration [5, 6].
The phenomenon of the drill bit torsion and stick-slip vibration could be directly observed by measuring the drill bit rotary speed [7, 8], and research on the drill bit vibration is further supported by the field data with the development of near bit measurement technology [9]. The process that the bit contacts and breaks formation rock is nonlinearity, complicated and hard to be predicted [10]. This will inevitably lead the drill bit vibration to present an extremely complex dynamics. Ref. [11, 12] studied on the rock machining by recurrences using the signal processing including the dynamical indicators like entropy, laminarity, determinism and also non-staconarity. Although some theoretical models of the drillstring [13] were established to present the chaotic dynamics, but no further use of field data for validation. As drill string torsional vibration can easily cause fatigue failure, many researchers undertaken extensive research on the control methods of torsional or stick-slip vibration. However, most control models are idealized. In the actual drilling process, the drill string torsional vibration is affected by many factors, and is an uncertain dynamic process, so establishing a precise model is impossible. We need to quantitatively research inherent nature of drill twist or stick-slip vibration based on the field measurement data in order to further study the mechanical process that the drill bit breaks rock and to provide a theoretical basis for establishment of stick-slip vibration control model.
For quantitative research of the drill bit torsional vibration, timely measurement of rotary speed near the bit is necessary. In this article a Strap-down Magnetic Based MWD System is developed, which can timely measurement of the drill bit rotary speed. The sampling frequency is up to 100 Hz. Vibration signals are sampled and stored during the drilling process, and then the data would be playback after the drilling. We could get massive time-series of the drill bit rotational speed. By reconstruction of phase space, calculation of correlation dimension and the largest Lyapunov exponent [12, 14], the existence of chaotic phenomenon during drill bit torsional vibration is proved by field data for the first time.
2. Data acquisition
2.1. The installation of the measurement system
The present MWD surveying system incorporate three-axis magnetometers and three-axis accelerometers arranged in three mutually orthogonal directions [15, 16], which are installed inside the nonmagnetic drill collar. This special drill collar is usually designed for Monel metal to avoid the external interferences with the measurements taken by the magnetometers [17]. Aboelmagd Noureldin [18] proposed that the nonmagnetic drill collar too expensive and developed the technology of fiber optic gyroscopes (FOG) has been suggested for MWD surveying of directional wells [19]. But gyroscope’s reliability is a problem, so this paper focuses on the magnetic surveying tools that have a wider range of applications. The installing structure of the downhole measurement system shows in Fig. 1. That is conducted by triaxial accelerometer and triaxial magnetometers, and redundancy design is adopted.
Fig. 1Measurement system (Left is the simplified diagram of bottom-hole assembly; Middle is the construction of measurement system; Right is installed structure of sensors)
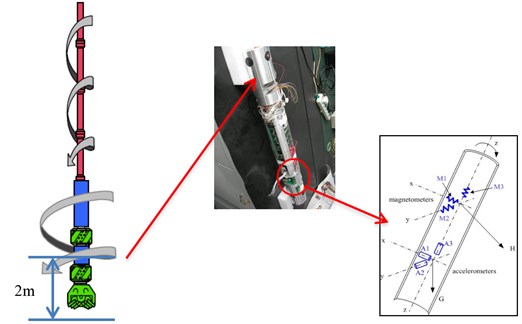
Assume the acceleration of gravity as , Earth’s magnetic field strength as . , , are respectively defined as survey gravity signals of triaxial accelerometers on the axis, obviously, are respectively defined as survey signals of triaxial magnetometers on the axis, and . When the rotational speed of the drillstring is 120 r/min, it can generate 50 measurement velocity data points when the drillstring rotates one lap.
Performance characteristics of the accelerometers and magnetometers are summarized in Table 1.
Table 1Characteristics of sensors
Parameter | Accelerometers (MS9010) | Magnetometers (CTM-DT06) |
Range | ±10 g | ±100000 nT |
Scale Factor | 200 mV/g | 5 V/G ± 5 % |
Nonlinearity | 0.8 % of SF | – |
Bias calibration | < 50 mg | ±0.005 G |
Noise | 0.140 mg/√Hz | ≤ 0.1 nT |
Bandwidth | 1000 Hz | 350 Hz |
2.2. Calculation of the drill bit rotational speed
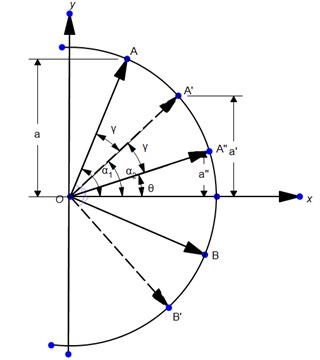
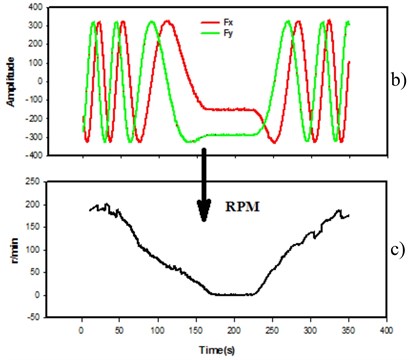
In the process of drilling, a magnetometers in the center of the drillstring will draw an approximate sinusoidal course with the drillstring rotation, but the drillstring rotation speed is variable, so the measurement curve is not strictly sinusoidal (Fig. 2(b)). From the theoretic point of view, a single axis magnetometer signal should be sufficient for the determination of the drillstring rotational speed, as shown in Fig. 2(a). Assuming that the drill callor radius is , is a central axis direction of the magnetometer, is the horizontal projection of the Earth’s magnetic field, obviously, , after the time , , respectively, magnetometer rotates to , from , when the measured values are proportional to , , . The following equtions can be obtained:
where expressed or which any one, we can solve the angle according the Eq. (1)-(3):
The drillstring rotates the angle of in the time of , accordingly solving the rotation speed. This equation, however, is the inverse cosine function, whose definition domain is This characteristic will bring a challenge in downhole data processing.
Because and the triaxial magnetometers were mounted vertically with each other on the axis, there will be 90° phase difference between and , as shown in the Fig. 2(a). When transfers from to , will transfer from to at the same time. The measurement signals as show in Fig. 2(b) is obtained from filed experiments.
Then:
Fig. 2The fluxgate rotation measurement calculation of the rotation speed diagram
a)
Thus , drillstring rotational speed () can be defined as follows:
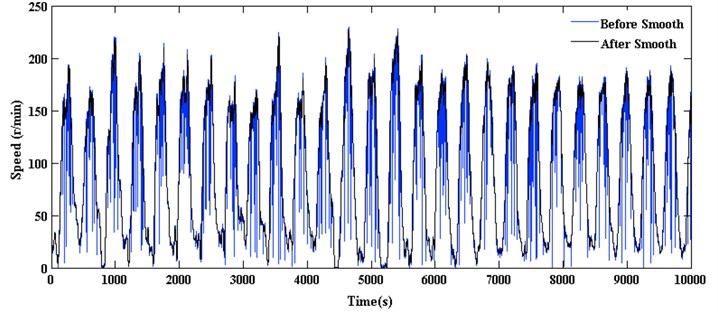
The definition domain of arctangent is , superior to the former algorithms. The speed value calculated is determined using the moving average filter for further processing, according Eq. (7). The smooth results as show in Fig. 3, therefore, it is conducive for the subsequent analysis when the speed value is smoother:
Fig. 3Rotational speed time series (using 10000 data points)
Finally, the drillstring time series is shown in Fig. 2(c) and Fig. 3. Since using synchronization calculating, it can be considered that the sampling rate of the rotational speed is 100 Hz. The dynamics of the drill bit torsional vibration will be revealed by the following nonlinear analysis of the measurement signal time series.
Assume the drill bit rotational speed time series finally resolved as , ,…, , then the time series of rotation angle is , ,…, , sampling frequency is 100 Hz, then the rotation angle and rotation speed satisfy the following equation:
3. Nonlinear analysis
In order to investigate the deterministic chaos in time series we use the phase-space reconstruction method to reconstruct an attractor that preserves the invariant characteristics of the original attractor. Before applying chaotic tools analysis in the time series we apply the “stationarity test” to check for the stationarity of the dynamics. We estimated the correlation dimension and the largest Lyapunov exponent in order to estimate the invariants of the attractor.
3.1. Phase-space reconstruction
The dynamics of the time series , ,…, are fully captured or embedded in the -dimensional phase space, where is the dimension of the original attractor. A vector in the reconstructed phase space is constructed from the time series as follows:
where is the delay time.
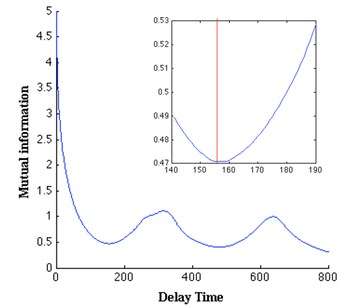
We apply the mutual information [20] to estimate a proper embedding delay , Fraser and Swinney [20] considered to use the first minimum of the mutual information as the optimal embedding delay. The first minimum of the mutual information calculated for the rotational speed time series is obtained at 157 (Fig. 4(a)), which is also the value that we will use in all-subsequent calculations. We use Cao’s method [21] to determine the embedding dimension. It computes and for the data set of dimension 1 up to a dimension of which is the largest embedding dimension used for calculating. and are defined as follows:
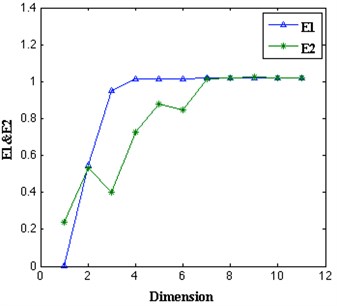
wherein is the embedding dimension, is the number of data points, is the embedding delay, and is the th vector in the data sets and its nearest neighbors of -dimensional phase space [22]. Calculating both and to determine the minimum embedding dimension of the time series, and to distinguish deterministic data from random data. As shown in Fig. 4(b), clearly the minimum embedding dimension is 7.
The signals, which have chaotic characteristic, usually seem to be random, especially when the nonlinear invariants are similar to the noise. We are not fully aware of the nature of the drillstring vibration signals that perform as time series, the fluctuation of parameter in the Cao’s method can be used as a measurement of uncertainty. When the system is chaos, will gradually increase to one from zero as the embedding dimension increases. When the random of the sequences enhances, the fluctuation range of will become smaller and smaller, finally, will approach to constant when the system is completely random, since there is no correlation between the data sets.
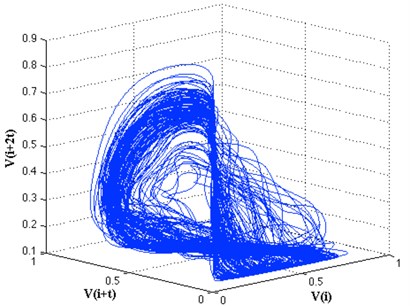
Having calculated the optimal and , we are able to successfully reconstruct the phase space of the system. For 157 and 7, the 3D projection of the attractor obtained according to Eq. (9) is presented in Fig. 5. The correct phase space reconstruction is a key step that enables further analysis of the dynamics associated with the torsional vibration.
Fig. 4Determination of the proper delay time and embedding dimension of the torsional vibration: a) the mutual information has the first minimum at τ= 157, b) the minimum embedding dimension is 7
a)
b)
Fig. 5Three-dimensional projection of the reconstructed phase space (obtained with embedding parameters: τ= 157 and m= 7)
3.2. Stationarity test
Since linear statistics, such as the mean or standard data deviation, usually do not possess enough discrimination power when analyzing irregular signals, nonlinear statistics have to be applied. We apply the stationarity test [23] program “stationarity.exe” [24] provided by [24] Matjaž Perc. They split the time series into several short non-overlapping segments and then use a particular data segment to make predictions in another data segment. By calculating the cross-prediction error () when considering points in segment to make predictions in segment , the cross-prediction error as a function of and then revels which segments differ in their dynamics. They obtained a very sensitive statistic capable of detecting changes in dynamics and thus a very powerful probe for stationarity.
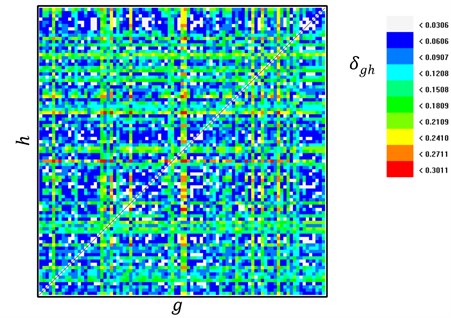
The average cross-prediction errors for all possible combinations of and are presented in Fig. 6. The whole time series was partitioned into 56 non-overlapping segments each occupying 1000 data points. The average value of all is 0.17, while the minimum and maximum values are 0.03 and 0.3, respectively. Since the maximal cross-prediction error is not one time larger than the average, we can determine that the studied time series is stationarity. We just consider only 1000 s of the torsional vibration time series. Otherwise, longer data sets of the vibration time series almost yield non-stationary.
Fig. 6Stationarity test. The color map displays average cross-prediction errors δgh in dependence on different segment combinations
3.3. Correlation dimension
After the reconstruction of time series in phase space, we can determine whether it have chaotic properties by calculating the chaotic invariants. Common chaotic invariants are correlation dimension [14], Kolmogorov entropy [25] and the Lyapunov exponent [26] and so on. The correlation dimension method is used for detecting the presence possibility of chaos. An algorithm proposed by Grassberger and Procaccia [14] is the most commonly applied method. According to this method the correlation sum, , is expressed as:
where is Heaviside step function defined as:
is the number of points in time series; is the radius of a sphere with its center at either of current points.
Then the correlation dimension is:
For the random process, varies linearly with increasing without reaching a saturation value. If the system is chaotic, the slope of vs converges to over an appropriate interval as increase.
In Fig. 9(a) we present the estimated slope as a function of for embedding dimensions 2 up to 10, where we see that a possible region of convergence the scaling region in the interval [–1.8, –0.6]. The estimated correlation dimension along with the estimated error as a function of the embedding dimension is presented in Fig. 9(b). We can estimate a correlation dimension in the range 2.0-3.0. This behavior indicates the possible existence of low-dimensional attractor with an estimated as .
Fig. 9a) Local slope of correlation sum; b) estimated dimension of the attractor for the data set
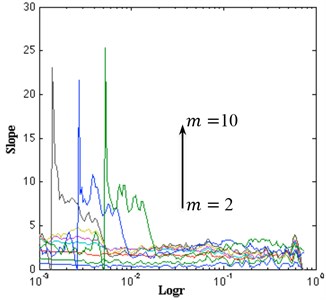
a)
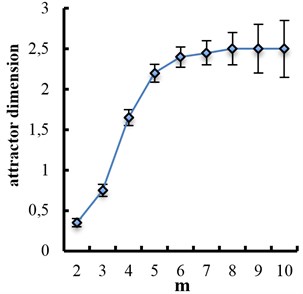
b)
3.4. Largest Lyapunov exponent (LLE)
The basic characteristics of chaotic motion are that the movement is extremely sensitive to initial conditions, two very close initial values resulting in orbit over time by separating exponentially, Lyapunov exponent [26-28] that describes the amount of this phenomenon.
Suppose chaotic time series is , embedding dimension is , time delay is , then reconstruction phase space is:
Take the initial point of phase space as , suppose that its most neighboring point is , the distance between two points is , from time to start tracking the time evolution of these two points, until the space between the two points exceeds a predetermined value on the moment :
Retain point , suppose its most neighboring point as , then:
Fig. 10Calculation of the maximal Lyapunov exponent of the torsional vibration, the effective expansion rate S(n), of which the linear slope in dependence on n*dt (dt= 0.01) is a robust estimate for the largest Lyapunov exponent
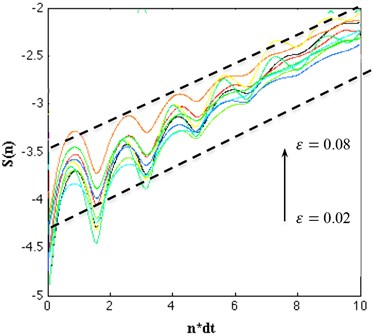
And makes the angle between and as small as possible, repeat the above procedure until reaches the end of the time series, the total number of iterations is , then the Largest Lyapunov exponent will be obtained:
In order to estimate the largest Lyapunov exponent we employed the methodology of Kantz [26] using the program “lyapmaxk.exe” [27] provided by Matjaž Perc. The results obtained for are presented in Fig. 10. The function shows a rather robust linear increase from 500 to 1000 for all . Thus, the slope of , indicated by the two linear lines, is a good estimate for the largest Lyapunov exponent of the system. The largest Lyapunov exponent is calculated through least-squares line fit for the time series and is found to be 0.15. This positive value indicates exponential divergence of trajectories and hences an evidence of chaos.
4. Conclusions
The data collected during hundreds of hours of drilling will be a massive time series. In order to reduce the amount of calculation, a typical section of time series is selected to be research object. Take a long segment of data to conduct an overall analysis of the drilling process. We use largest Lyapunov exponent as an observed parameters to analyze the low-dimensional chaos during the entire drilling process. The results show that chaotic phenomenon of the drilling bit torsional vibration exists in the whole drilling process.
For the torsional vibration of drill string, based on the field test data, previous studies focused on the detection and control of torsional vibrations, and the torsional vibration detection only divided into several different levels according to the severity. Nonlinear characteristics of torsional vibration were not conducted in-depth analysis. Although many articles discussed about nonlinear even chaotic characteristics of drillstring on theoretical models, but these studies have not been well supported by field test.
In field measurement data of torsional vibration, finding chaotic characteristics is helpful to rediscover the torsional vibration phenomenon, and to improve control algorithm of torsional vibration in engineering. Moreover, the phenomenon of torsional vibration is mainly due to the uneven force imposed by the bit breaking rock. Analysis of chaos helps to further improve bit rock-breaking theory. Through this research, we concluded the following conclusions:
1) Near-bit strap down MWD system can achieve real-time downhole measurement of rotational speed, fluxgate measurement data is used to solve rotational speed, and sampling frequency is up to 100 Hz.
2) Apply the mutual information and Cao’s method, obtain the optimal delay time is 157, and the embedding dimension is 7, the largest Lyapunov exponent calculated of velocity time series is 0.15. Moreover, the correlation dimension is 2.4, also verifies the existence of low-dimensional chaotic in bit torsional vibration.
3) Chaotic phenomena of the drilling bit torsional vibration exist in the whole drilling process.
4) Chaotic analysis on torsional vibration time series can help to further improve the torsional vibration of the drill string and drill bit rock-breaking theory, and it provides a new way for the drill string torsional vibration control method.
References
-
Cunningham R. A. Analysis of downhole measurements of drill string forces and motions. Journal of Engineering for Industry-Transactions of the ASME, Vol. 90, Issue 2, 1968, p. 208-216.
-
Belokobyl’skii S. V., Prokopov V. K. Friction induced self-excited vibration of drill rig with exponential drag law. Soviet Applied Mechanics, Vol. 18, Issue 12, 1982, p. 1134-1138.
-
Zamudio C. A., Tlusty J. L., Dareing D. W. Self-excited vibrations in drillstrings. SPE Annual Technical Conference and Exhibition, Dallas, Texas, 1987.
-
Brett J. Ford The genesis of bit-induced torsional drillstring vibrations. SPE Drilling Engineering, Vol. 7, Issue 3, 1992, p. 168-174.
-
Detournay E., DefournyP. A phenomenological model of the drilling action of drag bits. International Journal of Rock Mechanics and Mining Sciences, Vol. 29, Issue 1, 1992, p. 13-23.
-
Lin Y. Q., Wang Y. H. Stick-slip vibration of drill strings. Transactions of ASME, Journal of Engineering for Industry, Vol. 113, Issue 1, 1991, p. 38-43.
-
Robnett E. W., Hood J. A., Heisig G., et al. Analysis of the stick-slip phenomenon using downhole drillstring rotation data. SPE/IADC Drilling Conference, Amsterdam, Netherlands, 1999.
-
Sugiura J. The use of the near-bit vibration sensor while drilling lead to optimized rotary-steerable drilling in push-and point-the-bit configurations. SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, 2008.
-
Ledgerwood III L. W., Hoffmann Olivier J., et al. Downhole vibration measurement, monitoring and modeling reveal stick-slip as a primary cause of pdc bit damage in today’s applications. SPE Annual Technical Conference and Exhibition, Florence, Italy, 2010.
-
Richard T., Detournay E., Fear M., et al. Influence of bit-rock interaction on stick-slip vibrations of PDC bits. SPE Annual Technical Conference and Exhibition, San Antonio, Texas, 2002.
-
Litak G., Syta A., Gajewski J., Jonak J. Detecting and identifying non-stationary courses in the ripping head power consumption by recurrence plots. Meccanica, Vol. 45, Issue 4, 2010, p. 603-608.
-
Litak G., Syta A., Gajewski J., Jonak J. Nonlinear analysis of the ripping head power time series. Journal of Vibroengineering, Vol. 13, Issue 1, 2011, p. 39-51.
-
Mongkolcheep K., Palazzolo A., Ruimi A., et al. A modal approach for chaotic vibrations of a drillstring. ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, California, USA, 2009.
-
Grassberger P., Procaccia I. Measuring the strangeness of strange attractors. Physica D: Nonlinear Phenomena, Vol. 9, Issues 1-2, 1983, p. 189-208.
-
Russel M. K., Russel A. W. Surveying of boreholes. U.S. Patent 4163324, 1979.
-
Thorogood John L., Knott David R. Surveying techniques with a solid state magnetic multi-shot device. SPE Drilling Engineering. Vol. 5, Issue 3, 1990, p. 209-214.
-
Rehm W. A., Garcia A. Horizontal drilling in mature oil fields. SPE/IADC Drilling Conference, New Orleans, Louisiana, 1989.
-
Aboelmagd Noureldin, Dave Irvine-Halliday, Martin P. Mintchev Accuracy limitations of fog-based continuous measurement-while-drilling surveying instruments for horizontal wells. IEEE Transactions on Instrumentation and Measurement, Vol. 51, Issue 6, 2002, p. 1177-1191.
-
Noureldin A., Tabler H., Irvine-Halliday D., Mintchev M. P. Quantitative study of the applicability of fiber optic gyroscopes for MWD borehole surveying. SPE Journal, Vol. 5, Issue 4, 2000, p. 363-370.
-
Fraser A. M., Swinney H. L. Independent coordinates for strange attractors from mutual information. Physical Review A, Vol. 33, Issue 2, p. 1134-1140.
-
Cao Liangyue Practical method for determining the minimum embedding dimension of a scalar time series. Physica D: Nonlinear Phenomena, Vol. 110, Issue 1, 1997, p. 43-50.
-
Kennel M. B., Brown R., Abarbanel H. D. I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Physical Review A, Vol. 45, 1992, p. 3403-3411.
-
Schreiber T. Detecting and analyzing nonstationarity in a time series with nonlinear cross-predictions. Physical Review Letters, Vol. 78, 1997, p. 843-846.
-
Matjaž Perc Nonlinear time series analysis of the human electrocardiogram. European Journal of Physics, Vol. 26, Issue 5, 2005, p. 757-768.
-
Grassberger P., Procaccia I. Estimation of the Kolmogorov entropy from a chaotic signal. Physical Review A, Vol. 28, Issue 4, 1983, p. 2591-2593.
-
Wolf A., Swift J. B., Swinney H. L., et al. Determining Lyapunov exponents from a time series. Physica D: Nonlinear Phenomena, Vol. 16, Issue 3, 1985, p. 285-317.
-
Rosenstein M. T., Collins J. J., De Luca C. J. Apractical method for calculating largest Lyapunov exponents from small data sets. Physics D, Vol. 65, 1993, p. 117-134.
-
Kantz H. A robust method to estimate the maximal Lyapunov exponent of a time series. Physics Letters A, Vol. 185, 1994, p. 77-87.
-
MatjažPerc The dynamics of human gait. European Journal of Physics, Vol. 26, Issue 3, 2005, p. 525-534.
About this article
The authors express their appreciation to Drilling Technology Research Institute, Shengli Petroleum Administration of Sinopec Corp for providing materials and data and allowing the publication of this paper. Also, thanks for the Supported by the “863” Project “Strap Down Automatic Vertical Drilling System Engineering R&D” (2009AA093501); The Public Welfare Fund Project from The Ministry of Land and Resources (201411054).
