Abstract
To enhance the compacting performance and the asphalt density during the tamper-asphalt mixture interaction (TAMI), a dynamics model of the TAMI is established to analyze the compacting energy of TAMI under the different excitation frequencies of the compacting mechanism. The MATLAB/Simulink software is then applied to solve the vibration equations of TAMI based on the lumped parameters of the compacting mechanism and hot mix asphalt. The experimental research is also performed to verify simulation results and force distribution characteristics of the compacting mechanism on the asphalt pavement. The research results indicate that the vibration excitation of the compacting mechanism should be used in a range from 18 to 22 Hz and the number of vibrations of the compacting mechanism at the same position should be used by 4 or 5 to improve the compacting performance and the asphalt density. Additionally, the experimental results also show that the compacting force distribution of compacting mechanisms is asymmetric, thus, the design parameters of the vibration screed system should be optimized to enhance the compacting performance of the asphalt paver.
1. Introduction
The asphalt pavers were used for paving asphalt pavements with high power and efficiency requirements. The structure of asphalt pavers consisted of a vibration screed used to pave the hot mix asphalt onto the pavements and create the smooth surface in the paving process; and four pairs of the compacting mechanisms used to compress the hot mix asphalt on the pavements [1-4]. To increase the paving performance and uniformity of the hot mix asphalt paved on the pavements, the width of the vibration screed system of pavers was designed with its horizontal with of 9 or 12 m [5, 6]. However, the relatively long width of the screed combined with the vibration excitation forces of the compacting mechanism and the screed caused vibration for the vibration screed system, which affected the compacting performance and surface quality of the pavement [7, 8]. To solve this problem, the effect of the different excitation frequencies of the compacting mechanism and screed; and lumped parameters of the asphalt pavers were researched and evaluated [4, 7, 9, 10]. The researches showed that the dynamic parameters of the asphalt pavers strongly affected the paving performance and quality. The lumped parameters of the vibration screed system were then optimized to improve the paving performance [11]. Besides, the fuzzy control technology was also applied to further enhance the compacting performance of the asphalt pavers [1, 5, 6]. Based on the optimized and controlled results of the asphalt pavers, the increase of the paving performance and reduction of the vibration screed system were remarkably improved. However, the existing researches indicated that the paving performance and quality of the asphalt pavements were not only affected by the different parameters and compacting conditions of the asphalt pavers but also affected by the characteristics of the hot mix asphalts paved on the pavements.
The influence of the temperature, structure, and characteristic of the hot mix asphalt on the paving performance and quality of the pavements was also investigated via the methods of simulation and experimentation [1, 2, 12-14]. The studies showed that in the condition of the tamper-asphalt mixture interaction, the compacting density of the hot mix asphalt on the pavements could be maximum effective at the temperature of 85-100 °C and the particle size of 1-2 mm of the hot mix asphalt under the excitation frequency of 18-22 Hz of compacting mechanism, especially at 18 Hz. However, at these excitation frequencies, the quality of the paving pavement was also significantly reduced due to the increase of the shaking vibration between the compacting mechanisms [5, 6, 15]. Additionally, in above the researches, the acceleration response of the compacting mechanisms and the settlement of the asphalt mixture were used as the objective functions to evaluate the paving performance. The compacting energy and the compacting force distribution of the compacting mechanism during the tamper-asphalt mixture interaction which can affect the compacting performance and asphalt density have not yet been analyzed and directly evaluated in the existing studies.
The elucidation of the compacting force response and the compacting energy of the compacting mechanism on the hot mix asphalt during the tamper-asphalt mixture interaction not only helps the researchers to better understand the compression characteristics of the hot mix asphalt but also serves as the basis for optimization of the properties of the hot mix asphalt and control of the compacting mechanism to achieve maximum compacting performance. Thus, the calculation and analysis of the force interaction between the compacting mechanism and hot mix asphalt to better understand the working characteristics of the asphalt paver on the asphalt pavement are necessary. In this study, based on the model of the vibration screed system of asphalt pavers, the dynamic model of the tamper-asphalt mixture interaction is then established to analyze the compacting force and energy of the tamper-asphalt mixture interaction under the different excitation frequencies of the compacting mechanism. The MATLAB/Simulink software is applied to solve the vibration equations of the tamper-asphalt mixture interaction based on the lumped parameters of the tamper mechanism and hot mix asphalt. The experimental research is also performed to evaluate the simulation results and force distribution characteristics of compacting mechanisms.
2. The tamper-asphalt mixture interaction
2.1. The dynamics model of the tamper-asphalt mixture interaction
The paving layer of asphalt material was created based on the compacting method. under impacting of the compacting mechanisms during periodic compaction of the tamper-asphalt mixture interaction, the hot mix asphalt was then added and compacted to a fixed volume. After several compression cycles, the air and moisture in the hot mix asphalt could be completely discharged, and the density of the asphalt layer could be increased [8, 16]. Based on the dynamics model of the vibration screed system in Ref. [5], as shown in Fig. 1(a), a dynamics model describing the interaction process between the compacting mechanism and the hot mix asphalt is then established in Fig. 1(b).
Fig. 1(b), is the moving speed of the asphalt paver, is the compacting force of the compacting mechanism, is the translational displacement of the compacting mechanism after each compaction cycle, is the stroke of the vibration tamper, is the compensation of the thickness of the hot mix asphalt, and is the thickness of the compressed asphalt layer.
As described in Fig. 1, the compaction process of the hot mix asphalt is divided into two stages including (1) the compacting mechanism falls from the top position of down to the lowest position of with the stroke of the vibration tamper to compact the hot mix asphalt (first compacting time), then, (2) the compacting mechanism moves from the lowest position of up to the top position of and creases a gap between the compacting mechanism and the hot mix asphalt. Under the impact of the vibration screed and the gravity of the hot mix asphalt, the hot mix asphalt in the vibration screed system is then added in the gap below the compacting mechanism, the compacting mechanism continues to fall back down to compress the added hot mix asphalt (second compacting time) to increase density and compactness of the asphalt pavement.
Fig. 1The dynamic model of the vibration screed system and tamper-asphalt interaction
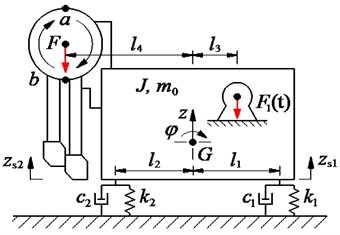
a) Vibration screed system model
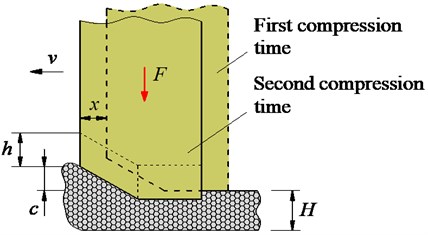
b) Tamper-asphalt mixture interaction model
Fig. 2Structure and model of the tamper-asphalt mixture interaction
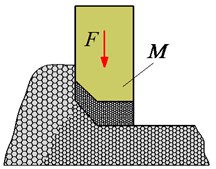
a) Practical compaction structure
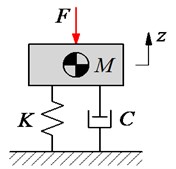
b) Equivalent compaction model
c) Compaction impulse
Due to the final density of the compacted hot mix asphalt being affected by the gradation of the asphalt material and its internal friction coefficient, therefore, the density of the asphalt mixture after compaction is indicated by [16, 17]:
where is the density of the hot mix asphalt, is the loss coefficient of compactness.
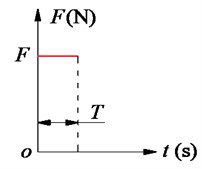
Additionally, during the paving process of the asphalt paver, the traveling speed of the paver is constant while the motion of the compacting mechanism is cyclic in the vertical direction. Thus, the compacting process of the asphalt pavement is actually a combination of horizontal and vertical movements, and . Therefore, the compacting force of the paver-asphalt mixture interaction and the paving quality are affected by both the traveling speed of the pave and the excitation frequency of the compacting mechanism. To elucidate the compacting energy and force distribution of the tamper mechanism on the hot mix asphalt during the tamper-asphalt mixture interaction in Fig. 2(a), a vibration model of the tamper-asphalt mixture interaction is then established Fig. 2(b). Based on the working principle of the compacting mechanism, the impacting force of the compacting mechanism on the asphalt pavement received by a rectangular pulse, as described in Fig. 2(c) [12-13, 18], is used as the excitation force to calculate the compacting force impulse of the tamper-asphalt mixture interaction. Fig. 2, is the mass of the tamper-asphalt mixture interaction determined the asphalt mixture after compaction , parameters of , , and , and mass of the compacting mechanisms. and are the stiffness and damping coefficients. is the excitation force of the compacting mechanism described by a rectangular pulse with unit pulse (N) and excitation time (s).
Based on the dynamic model in Fig. 2(b) and application of Newton’s second law, the dynamic differential equation of the tamper-asphalt mixture interaction is given by:
Due to the vibration excitation force of the system being a constant in excitation time (s), therefore, the solution of Eq. (2) is obtained as follows [19]:
where is the natural frequency of the system, is the damping natural frequency, and is the damping ratio of the asphalt material.
At the initial time 0 before the unit pulse is applied, the state of the tamper-asphalt mixture interaction is a static state. According to the momentum theorem, the momentum is determined by . Therefore, the unit impulse response of the asphalt layer is:
2.2. Numerical simulation results
Based on the actual structure of the vibration screed system and the dynamic parameter of the tamper-asphalt mixture interaction listed in Table 1 [17], the natural frequency of the system, the damping ratio of the asphalt material, and the damping natural frequency in Eq. (3) are determined by:
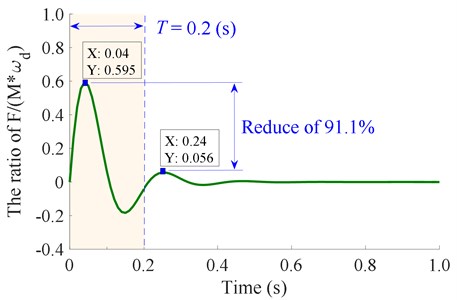
Thus, the unit impulse response of calculated in Eq. (4) is simulated and plotted in Fig. (3). Observing the result in Fig. (3), we can see that the unit impulse response of the asphalt material in the tamper-asphalt mixture interaction condition is an attenuation signal with a decay cycle of 2×3.14/29.5 ≈ 0.2 (s). Due to the vibration frequency of the compacting mechanism could being changed from 0 to 22 Hz [5-6], thus, the minimum/ maximum vibration time of a cycle of the compacting mechanism is 1/22 ≈ 0.045 (s) and its ∞. Because the energy () of the tamper-asphalt mixture interaction in one decay cycle is strongly reduced by 91.1 %, as shown in Fig. 3. Therefore, the compacting mechanism needs to ensure that it retains the previous vibration energy before the next vibration pulse occurs. To satisfy this requirement, the maximum vibration time of a cycle of the compacting mechanism should be smaller than the decay cycle 0.2 (s) of the tamper-asphalt mixture interaction in Fig. 3, which means the vibration frequency of the compacting mechanism must be greater than 5 Hz ( 1/0.2 = 5 Hz).
Additionally, the compacting energy of a single vibration cycle is quickly reduced up to 91.1 %, thus, it is necessary to perform multiple vibrations of the compacting mechanism on the same compaction cycle of the tamper-asphalt mixture interaction. With the width , moving speed , and frequency of multiple vibrations of the compacting force of the compacting mechanism at the same position, the number of vibrations of the compacting mechanism at the same position is defined as follows:
where the result of is 1, 2, 3, 4, 5, ..., or , and depends on the ratio of .
Table 1The parameters of steel-asphalt contact
Parameters | Value |
Type of contact | Steel-asphalt contact |
/ kg | 3083 |
/ N·m-1 | 3.06×106 |
/ N·s·m-1 | 68×103 |
/ m | 25×10-3 |
/ m·s-1 | 0.1 |
/ Hz | 0-22 |
Fig. 3The excitation impulse of a single shock
Therefore, the compacting force of the compacting mechanism at the same position should be added by multiple vibrations and the equation of is described by [5]. Thereby, Eq. (4) is rewritten by:
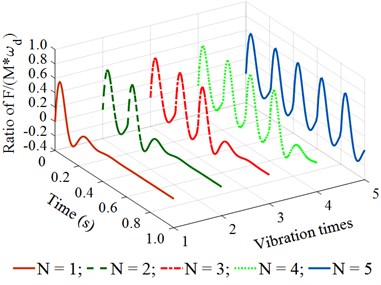
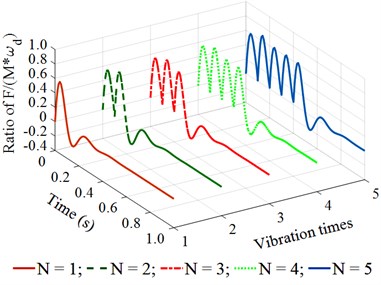
With the is constant, the ratio of should be chosen to satisfy the condition of 1, 2, 3, 4, 5, ..., to ensure the paving quality (because frequency and speed affect the paving quality) and retain the previous vibration energy before the next vibration pulse occurs. Based on the working parameters of the asphalt paver listed in Table 1, the maximum value of is determined by 25×10-3×22/0.1 = 5.5, therefore, 1, 2, 3, 4, 5 is chosen to simulate and evaluate the compacting performance and vibration energy of the compacting mechanism during the tamper-asphalt mixture interaction under the different frequencies of the compacting mechanism 5, 10, 14, 18, 22, and 26 Hz. The simulation results are shown in Fig. 4.
Observing the results in Fig. 4(a) and 4(b), we can see that when the vibration frequency is from 5 to 10 Hz under different vibration times of 1, 2, 3, 4, or 5, the remaining energy in the time of 0 to 0.2 (s) of a vibration cycle is too small. This is the reason that the achieved compression efficiency of the asphalt paver in Refs. [5, 6] is very low. When the vibration frequency is from 14 to 18 Hz under different vibration times of 1, 2, 3, 4, or 5, the results in Fig. 4(c) and 4(d) show that the remaining energy in the time of 0 to 0.2 (s) of a vibration cycle is significantly increased, especially at 4 and 5. This means that the density of the compacted hot mix asphalt is increased, thus, the compaction performance of the asphalt pavement is improved. Similarly, with the vibration frequency from 22 to 26 Hz and under different vibration times of , the results in Fig. 4(e) and 4(f) indicate that the compacting energy of the compacting mechanism is increased while its remaining energy at 0.2 (s) in a vibration cycle before the next vibration pulse occurs is quite high, particularly at 5. Thus, the asphalt density and compression efficiency of the asphalt paver are remarkably improved under these vibration frequencies. These simulation results are similar to the experimental results of Ref. [17]. However, the existing researches have not clearly explained the compaction energy and compaction characteristic in the tamper-asphalt mixture interaction.
Fig. 4The stimulating impulse response of the tamper-asphalt mixture interaction under the different excitations of the compacting mechanism
a) At an excitation frequency of 5 Hz
b) At an excitation frequency of 10 Hz
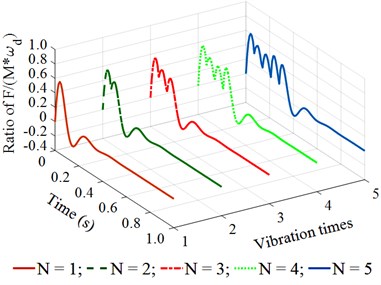
c) At an excitation frequency of 14 Hz
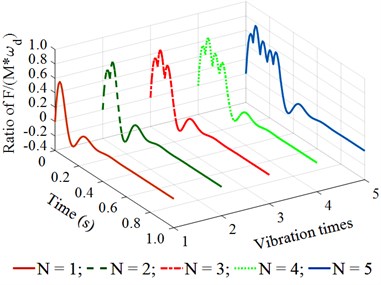
d) At an excitation frequency of 18 Hz
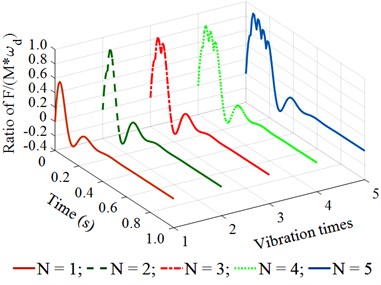
e) At an excitation frequency of 22 Hz
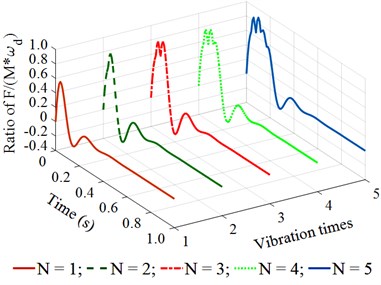
f) At an excitation frequency of 26 Hz
With 5, the comparison results in Fig. 5 show that the remaining energy at 0.2 (s) of 5, 10, and 14 Hz is quite low while both the compacting energy and the remaining energy at 0.2 (s) of 18, 22, and 26 Hz are quite high. Therefore, based on the operating parameters of the asphalt pavers as the speed and vibration frequency, 5 and 18 to 22 Hz should be used to improve the compacting performance and the asphalt pavement density. To verify the numerical simulation results, the experimental study of the tamper-asphalt mixture interaction is performed as below.
Fig. 5The stimulating impulse response of the tamper-asphalt mixture interaction at N= 5 under the different excitations of the compacting mechanism
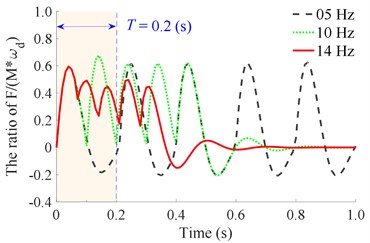
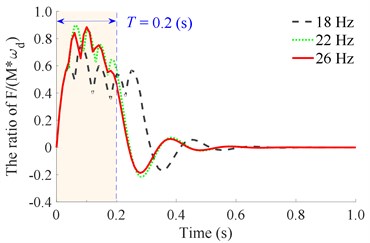
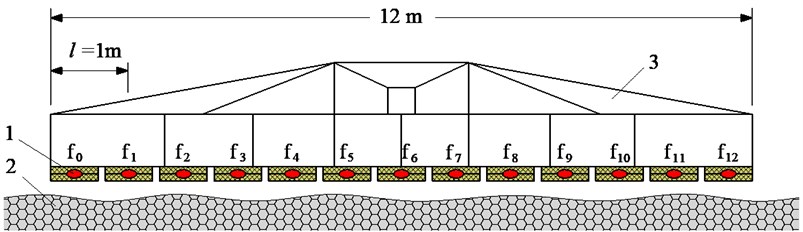
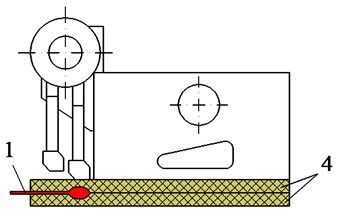
Fig. 6The experimental model of the tamper-asphalt mixture interaction: 1 – force sensor, 2 – asphalt pavement, 3 – compacting mechanism, 4 – two planks of hard rubber material
a) Front view of the compacting mechanism
b) Side view of the compacting mechanism
c) Model of force sensor setup
3. Experimental study of the tamper-asphalt mixture interaction
3.1. Experimental setup process
It is very difficult to measure the compressive force response of the tamper-asphalt mixture interaction in the actual condition due to the difficulty in determining the pressure and the compressive density of the compacted hot mix asphalt. To solve this issue, 13 pairs of hard rubber material sheets with their properties that are equivalent to that of hot mix asphalt are used to measure the compressive pressure and density of the tamper-asphalt mixture interaction, as shown in Figs. 6(a) and 7(a). At each pair of hard rubber material sheets installed below the compacting mechanism, a force sensor is installed in between two rubber plates, as plotted in Figs. 6(b), 6(c), and 7(b). The measured results are then computed and analyzed via the analysis system of Belgium LMS, as provided in Fig. 7(c).
Fig. 7The actual structure of the asphalt paver and its experimental setup process

a) Experimental setup of the compacting mechanism

b) Force sensor

c) Signal processor and display the results
Under the impact of the compacting force of the compacting mechanism in the vertical direction, the pressure distributed evenly on the upper surface of the rubber pad, accordingly, the displacements in the and directions of the pair of rubber pads are 0 meanwhile the vertical displacements at upper and lower rubber pads are and 0, as described in Fig. 6(c). Therefore, the displacement and stress in the vertical direction at depth of the rubber pads are determined by [20]:
where , , and are e Poisson’s coefficient, density, and Young modulus of the rubber material, respectively.
At the installation position of the force sensor, the compressive stress of the rubber material has a linear relationship with the pressure . Therefore, the pressure of the asphalt layer can be determined through the pressure in the rubber pads. The measurement process is then performed as below.
3.2. Discussion of the measured results
The measurement process is performed with 5 under the different excitation frequencies of the compacting mechanisms {5, 10, 18, and 22} Hz corresponding to two different excitation frequencies of the vibration screed {0 and 22.5} Hz. The experimental results of the stimulating impulse response and the compacting force distribution of compacting mechanisms on the asphalt pavement during the tamper-asphalt mixture interaction are plotted in Figs. 8 and 9, respectively.
Observing the comparison results between the measurement and simulation at the excitation frequencies of 10 and 22 Hz with 5 in Fig. 8(a) and 8(b), we can see that the curves of the stimulating impulse response between the measured and simulation results are similar. Therefore, the mathematical model and the numerical simulation result of the tamper-asphalt mixture interaction could be reliable.
Fig. 8The experimentation and simulation results of the stimulating impulse response of the tamper-asphalt mixture interaction at N= 5
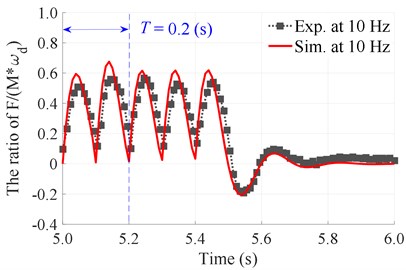
a) At an excitation frequency of 10 Hz
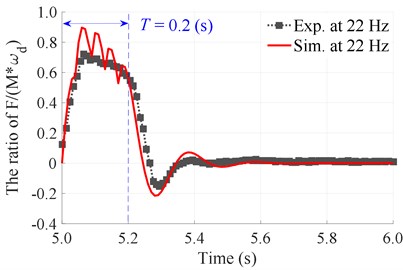
b) At an excitation frequency of 22 Hz
Fig. 9The experimental result of the compacting force distribution of compacting mechanisms during the tamper-asphalt mixture interaction
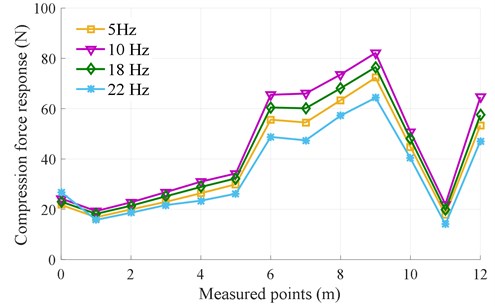
a) Without the excitation frequency of the screed, 0.0 Hz
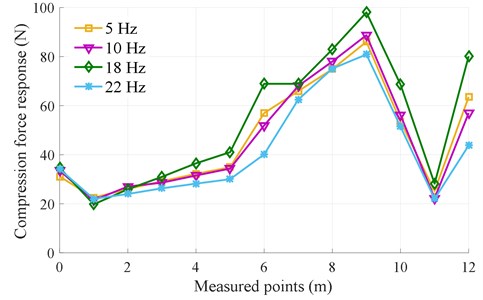
b) With 50 % of the excitation frequency of the screed, 22.5 Hz
Additionally, the results of the compacting force distribution of compacting mechanisms on the asphalt pavement in Fig. 9(a) without the excitation of the screed and Fig. 9(b) with using 50 % of the excitation of the screed show that the excitation frequency substantially affect the compacting force of the compacting mechanisms. In the case of ignoring the excitation of the screed ( 0.0 Hz), the measured result in Fig. 9(a) indicates that the compacting force is increased with the increase of from 5 to 10 Hz, the compacting force is then reduced with the increase of from 18 to 22 Hz, and the maximum compacting force is obtained at 10 Hz. Especially, the average value of the compacting force at 10 Hz is increased by 22.54 % in comparison with that of 22 Hz, as listed in Table 2.
Table 2The average values of the compacting force response (F-) under the different excitations of fc
The average values of (N) | The different excitations of (Hz) | |||
5 (Hz) | 10 (Hz) | 18 (Hz) | 22 (Hz) | |
0.0 (Hz) | 38.43 | 44.85 | 41.50 | 34.74 |
22.5 (Hz) | 46.31 | 46.04 | 52.66 | 41.57 |
In the case of the compacting mechanisms using 50 % of the excitation of the screed ( 22.5 Hz), the measured result in Fig. 9(b) also is similar to that without the excitation of the screed in Fig. 9(a). However, the maximum compacting force is obtained at 18 Hz. Particularly, the average value of the compacting force at 18 Hz is increased by 21.05 % in comparison with that of 22 Hz, as listed in the same Table 2. Besides, under the effect of the excitation frequency of the screed , the average values of the compacting force with using 22.5 Hz are higher than that without the excitation frequency of the screed. Especially, the maximum average value of the compacting force with using 50 % of the excitation of the screed is significantly increased by 21.19 % compared to that of without the excitation of the screed. This could be due to the influence of the vibration excitation of the screed. The maximum compacting force at 18 Hz implies that the compression efficiency and asphalt density achieved are maximum. These measured results are similar to the results in Ref. [5]. Besides, the measured results in both Figs. 9(a) and 9(b) show that the compaction force responses at the measured points are remarkably skewed and asymmetrical, so the vibration screed system works are unstable and the paving quality is low. To solve this issue, the design parameters of the vibration screed system should be optimized to improve the paving performance of pavers.
4. Conclusions
Based on the mathematical model established to analyze the compacting energy and compacting force distribution during the tamper-asphalt mixture interaction via numerical simulation and experimentation, the research results can be summarized as follows:
1) To ensure that the compacting mechanism retains the previous vibration energy before the next vibration pulse occurs, the vibration excitation frequency of the compacting mechanism must be greater than 5 Hz.
2) To vibration excitation frequency of the compacting mechanism should be used in a range of 18 to 22 Hz and the number of vibrations of the compacting mechanism at the same position should be used by 4 or 5 to improve the compacting performance and the asphalt density.
3) Based on the experimental results, the compacting force distribution of compacting mechanisms on the asphalt pavement is asymmetric, thus, it is necessary to optimize the design parameters of the vibration screed system to reduce the influence of the specific frequency of the system on the compacting performance of the asphalt paver.
References
-
A. Amadore, G. Bosurgi, and O. Pellegrino, “Analysis of hot mix asphalt compaction data by means of fuzzy clustering techniques,” Construction and Building Materials, Vol. 40, pp. 430–437, Mar. 2013, https://doi.org/10.1016/j.conbuildmat.2012.09.082
-
Q. Xu, G. K. Chang, V. L. Gallivan, and R. D. Horan, “Influences of intelligent compaction uniformity on pavement performances of hot mix asphalt,” Construction and Building Materials, Vol. 30, pp. 746–752, May 2012, https://doi.org/10.1016/j.conbuildmat.2011.12.082
-
D. Luo, Z. Feng, and X. Wang, “Simulation and experimental study on compacting mechanism of asphalt paver,” Journal of Guangxi University, Vol. 35, pp. 729–735, 2011.
-
H. Hou et al., “Investigation on the pavement performance of asphalt mixture based on predicted dynamic modulus,” Construction and Building Materials, Vol. 106, pp. 11–17, Mar. 2016, https://doi.org/10.1016/j.conbuildmat.2015.10.178
-
N. Liem, P. Wang, and J. Zhang, “Experimental research and optimal control of vibration screed system (VSS) based on fuzzy control,” Journal of Vibroengineering, Vol. 22, No. 6, pp. 1415–1426, Sep. 2020, https://doi.org/10.21595/jve.2020.21560
-
V. Nguyen, Z. Wu, B. Zhang, and Z. J. Run, “Vibration analysis and control of a vibration screed system for asphalt pavers,” The International Journal of Acoustics and Vibration, Vol. 25, No. 3, pp. 363–372, Sep. 2020, https://doi.org/10.20855/ijav.2020.25.31649
-
K. Mollenhauer and M. P. Wistuba, “Influence of asphalt compaction procedure on 3D deformation properties,” International Journal of Pavement Engineering, Vol. 17, No. 1, pp. 5–12, Jan. 2016, https://doi.org/10.1080/10298436.2013.812213
-
Y. Wan and J. Jia, “Nonlinear dynamics of asphalt-screed interaction during compaction: application to improving paving density,” Construction and Building Materials, Vol. 202, pp. 363–373, Mar. 2019.
-
Z. Feng, L. Zhu, X. Wang, and L. Zhao, “Dynamic simulation and parametric selection for tamping mechanism of paving machines,” China Journal of Construction Machinery, Vol. 7, pp. 26–30, 2009.
-
D. Luo, Z. Feng, and X. Wang, “Parameter optimization for compacting system of asphalt paver based on response surface method,” Journal of Vibration and Shock, Vol. 31, pp. 92–95, 2012.
-
J. Jia, Y. Wan, and H. Liu, “Parameter optimization for a compaction system of vibration screed of an asphalt paver based on a multi-objective genetic algorithm,” Journal of Vibration and Shock, Vol. 36, pp. 230–235, 2017.
-
J. Jia, H. Liu, and Y. Wan, “Dynamic characteristics modelling of the tamper-asphalt mixture interaction: application to predict asphalt mat density,” International Journal of Pavement Engineering, Vol. 20, No. 5, pp. 530–543, May 2019, https://doi.org/10.1080/10298436.2017.1316642
-
M. Kim, L. N. Mohammad, P. Phaltane, and M. A. Elseifi, “Density and SCB measured fracture resistance of temperature segregated asphalt mixtures,” International Journal of Pavement Research and Technology, Vol. 10, No. 2, pp. 112–121, Mar. 2017, https://doi.org/10.1016/j.ijprt.2017.01.004
-
E. Kassem, W. Liu, T. Scullion, E. Masad, and A. Chowdhury, “Development of compaction monitoring system for asphalt pavements,” Construction and Building Materials, Vol. 96, pp. 334–345, Oct. 2015, https://doi.org/10.1016/j.conbuildmat.2015.07.041
-
H. Liu et al., “Investigation of paver screed on compaction characteristics of mixture,” China Journal of Highway and Transport, Vol. 29, pp. 152–157, 2016.
-
S. J. Xu Q., “Compacting principle and structural analysis of tamper mechanism for paver,” Road Machinery and Construction Mechanization, Vol. 23, pp. 15–17, 2006.
-
C. Yin, “Dynamic study and parameter optimization about screed and tamper mechanism of the paver,” M.S. Thesis, 2018.
-
J. Sun, G. Xu, and X. Wang, “Dynamics Analysis and Improvement of Screed based on Computer Simulation,” Journal of Multimedia, Vol. 8, No. 5, pp. 548–556, 2013, https://doi.org/10.4304/jmm.8.5.548-556
-
S. Singiresu, Mechanical Vibrations, 5th ed. New Jersey: Prentice Hall, 2010.
-
A. Bertram, Elasticity and Plasticity of Large Deformations, 3rd ed. Berlin: Springer, 2012.
About this article
This research is supported by the Key Project of Scientific Research Plan of Education Department of Hubei Province (No. D20204501), the Key Scientific Research Project of Hubei Polytechnic University (No. 21xjz02A), Open Fund Project of Hubei Key Laboratory of Intelligent Transportation Technology and Device, Hubei Polytechnic University (Nos. 2020XZ107, 2021XZ107), and National Key Research and Development Plan (No. 2019YFB2006402).
