Abstract
Different description results will be obtained when apply hidden Markov model (HMM) to the two different channel signals from the same data collection point respectively. Besides, wrong fault diagnosis result might be obtained because fault feature information would not be described comprehensively by using only one single channel signal. In theory, two channel signals collected form the same data collection point will contain much more fault information than the single channel signal contain, but the coupled phenomenon might occur between the two channel signals. Coupled hidden Markov model (CHMM) is the improved method of HMM and it can fuse the information of two channel signals from the same data collection point efficiently, so much more reliable diagnosis result could be obtained by using CHMM than by using HMM. Stated thus, the fault diagnosis method of rolling element bearing based on wavelet kernel component analysis (WKPCA)-CHMM is proposed: Firstly, use WKPCA as fault feature vectors extraction method to increase the efficiency of the proposed method. Then apply CHMM to the extracted fault feature vectors and satisfactory fault diagnosis result is obtained at last. The feasibility and advantages of the proposed method are verified through experiment.
1. Introduction
HMM has been used in fault diagnosis of rotating machinery widely [1-5]. However, it could not solve the multi-channel data fusion problem. Many machine condition monitoring techniques have been proposed based on multi-channel data acquisition system [6]. The current data fusion techniques are mainly classified into three categories: data-level fusion, feature-level fusion and decision-level fusion. Vibration and current signals were fused basing on Dempster-Shafer (DS) to improve the diagnostic accuracy [7]. Some vibration parameters such as RMS, peak and peak to peak were used in the detection defects in the bearing [8]. In order to obtain better diagnostic result, the waterfall fusion model was adopted by fusing information from two different kinds of sensors: the accelerometer and load cell [9]. CHMH [10] was first proposed as a novel sensory fusion architecture to solve the data fusion problem in audio-visual speech recognition (AVSR). Xie [11] proposed a coupled hidden Markov model approach to video-realistic speech animation and realistic facial animations driven by speaker independent continuous speech was realized. In paper [12] the dependent faults occurring over time were diagnosed successfully by the proposed coupled factorial hidden Markov model method. In paper [13] the spatial and temporal dynamics in multi-channel electrocorticographic (ECoG) time series was investigated using CHMM. Though CHMM has been used widely in the above stated aspects, very few papers presented its using in fault diagnosis of rolling element bearing. The CHMM was used in rolling element bearing fault diagnosis and performance degradation assessment respectively in paper [14] and paper [15], and satisfactory experiment analysis results were obtained. So the using of CHMM in fault diagnosis of rolling element bearing is studied and the WKPCA is used as feature extraction method in the paper.
2. Wavelet kernel principle component analysis
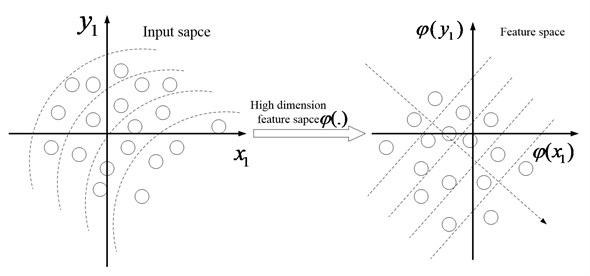
Various feature parameters are expected to be obtained so as to reflect the running state of the machinery comprehensively. However, the efficiency of the subsequent intelligent diagnosis will be decreased greatly when too many feature vectors are used as the input vectors. Besides, some of the feature parameters are redundant and useless which will decrease the accuracy of intelligent diagnosis to some extent. Principle components analysis (PCA) and the improved PCA method-kernel principle component analysis (KPCA) [16, 17] are the common used linear and non-linear feature dimensionality reduction methods to solve the above contradiction. The schematic diagrams of PCA and KPCA can be referred to Fig. 1 and Fig. 2. KPCA not only owns the virtues of PCA, but also can analyze the non-linear problems which PCA could not. Besides, the KPCA has other advantages which can be referred to the paper [18]. Though KPCA improve the PCA greatly, there are still some defects in the traditional KPCA: firstly, the selection of kernel function in the traditional KPCA is based on experience. Secondly, there is not criterion for selection of the relative parameters of kernel function. Any functions can be fitted by the wavelet function [19] in theory, so in the paper a novel features reduction method named WKPCA is proposed: the wavelet function is used as the kernel function instead of the common used radial basis function (RBF) in KPCA, and the wavelet function can increase the non-linear mapping ability of KPCA greatly. The relative definitions and theory of WKPCA are given as the following.
Fig. 1The schematic diagram of PCA
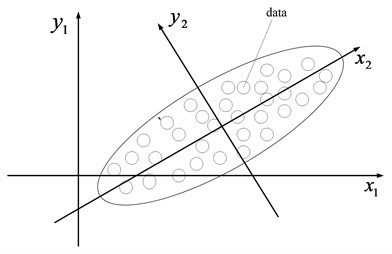
Fig. 2The schematic diagram of KPCA
Definition 1 [20]: Kernel is a function which satisfies the following equation for any :
where represents the transpose and represents a mapping from the data space to the feature space , and the relationship of them can be shown as following:
It not only can calculate the inner product more efficiently but also need not calculate mapping process explicitly. The kernel function must satisfy the requirement of Mercer [21].
Theorem 1 [22]: Supposing is a continuous symmetric function which makes the integral operator :
to be positive. That is to say the following relationship can be obtained:
In Eq. (4), the symbol represents convolution algorithm. could be used as the representation of dot product in the feature space if the above conditions can be satisfied.
The kernel function satisfies the requirement of Mercer which is given in theorem 2.
Theorem 2 [23]: If the translation invariant kernel function is an allowable kernel whose fourier transform (FT) must satisfy the following condition:
Wavelet function has the peculiar characteristics of multi-resolution analysis compared with the common used kernel functions such as RBF used in the traditional KPCA. The wavelet function can fit any function much more precisely, so the wavelet function is combined with PCA instead of the common used kernel function such as RBF, so much stronger non-linear mapping capability can be obtained. The combination of wavelet function with PCA is named wavelet kernel principal component analysis also called WKPCA for short.
Supposing is a mother wavelet function, , , and a translation invariant wavelet kernel function satisfying the requirement of Mercer can be constructed as following [22]:
where is the scale factor.
The requirement of Mercer is not only satisfied but also the properties of the wavelet function are considered when the wavelet kernel function is being constructed. The wavelet construction kernel function meeting the wavelet framework conditions has obvious advantage because it takes into account the sparseness of the training data and the complexity of the constructed kernel functions. Mexican hat wavelet function is a kernel function meeting the wavelet framework conditions [24]. The Mexican hat wavelet function shown in Eq. (7) is used to construct the translation invariant kernel function:
The constructed translation invariant wavelet kernel function is shown in Eq. (8):
The proof of Mexican hat wavelet satisfying Theorem 2 is given as following.
With regard to the Mexican hat wavelet shown in Eq. (9):
In Eq. (9), is the scale factor same as the meaning of shown in Eqs. (6) and (8). The Eq. (10) can be obtained:
From the above, the proof of Mexican hat wavelet satisfying Theorem 2 is obtained which can be used to construct the allowable kernel function.
3. CHMM
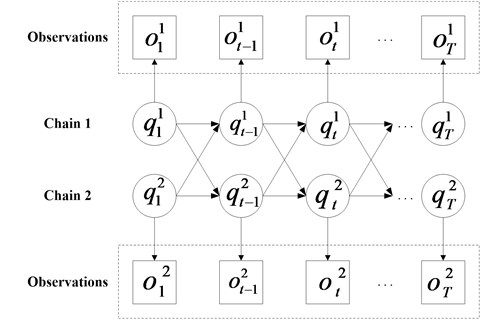
CHMM is constituted by multi-HMM chains which couple through cross-time and cross-chain conditional probabilities as illustrated in Fig. 3 and Fig. 4, and the CHMM can be regarded as a special case of dynamic Bayesian network. The observations of each chain in CHMM are decided by the corresponding state in the same chain. Besides, the unobservable state sequence can be only estimated by the observation sequence. The above two characteristics of CHMM are similar to HMM. Different from HMM, all the state variables in different chains may be contained at certain time slice in the states of the CHMM system. The states of all chains in the previous time slice decide the state in each chain. So much comprehensive fault diagnosis result of bearing can be obtained using CHMM because it has a potential to fuse data from multi-channel. The following is the basic theory introduction of a two-chain CHMM.
Fig. 3The schematic of HMM
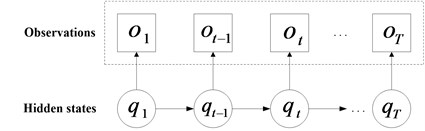
Fig. 4The schematic diagram of CHMM
3.1. Elements of CHMM
The chain index is represented by , i.e., . The total set of hidden states of each chain is represented as . Let represent the observation vector and the hidden state at time is expressed as . The following expression describes the elements of CHMM: .
(1) represents the state transition probability matrix. The system transfers from the state to the state with probability which could be represented by the following equation:
(2) The observation probability matrix is expressed as . The output generated by each state with a probability distribution function can used the following equation:
(3) The initial state distribution is , and the calculated probability value of the system’ initial state in is :
The probability distribution of continuous observation can use the Gaussian mixed model (GMM) as follows:
where is the number of Gaussian mixtures of chain in state , is the weight for each Gaussian mixture, and is a Gaussian density with mean vector and covariance matrix .
3.2. CHMM' basic problems
There are three basic problems existing for CHMM in real application:
(1) Evaluation. How the observation sequence with a given CHMM is computed, i.e., ?
(2) Decoding. Given the observation sequence and a CHMM , how do we select a hidden state sequence to explain the process, i.e., ?
(3) Learning. Given the observation sequence , how do we adjust the model parameters to maximize the probability ?
Many algorithms such as Viterbi algorithm, forward-backward procedure and Baum-Welch method were proposed to solve the above problems. The reference [21] gives more details about the above algorithms.
4. Experiment
The flow chart of the proposed method based on WKPCA-CHMM is shown in Fig. 5 and the specific details of each step are given as following:
Step 1: Data collection: collect the signals of the four states (normal state, outer race fault state, rolling element fault state and inner race fault state) of rolling element bearing using double channel accelerator sensors.
Table 1Time-domain statistics indexes
Calculation formulas | ||
1 | Peak | |
2 | Ppvalue | |
3 | Meanamp | |
4 | Rootamp | |
5 | Root mean square | |
6 | Waveind | |
7 | Pluseind | |
8 | Peakind | |
9 | Marginind | |
10 | Skewness | |
11 | Kurtosis | |
Remark: is time domain discrete signal | ||
Step 2: Data separation and feature extraction: separate the data of the eight channel signals into 50 groups (The 1-40th groups are used as CHMM training data and 41th-50th groups are used as testing data) respectively and 400 groups are obtained in all. There are 1024 points in each group. Apply the eleven time-domain statistical indexes (The 11 indexes and their corresponding calculation formulas are shown in Table 1) and one time-frequency domain index (the wavelet packet energy entropy (WE) which will be stated in the following chapter) to each group data.
Noting: The 11 indexes are the traditional common used time-domain statistical feature vectors and they can reflect the running state correctly when the fault signal is linear. The signals usually take on non-linear characteristic when fault occurs in machinery, so the time-frequency index is also need so as to capture the characteristic of the fault signal. In the paper, the wavelet packet energy entropy (WE) is used as time-frequency index which will be discussed in the Subsequent chapters.
Step 3: Dimensionality reduction: apply WKPCA to the feature vectors obtained in step 2 in order to obtain dimensionality reduction feature vectors.
Step 4: CHMM models training: use the dimensionality reduction training feature vectors to train four CHMM models (normal state CHMM, inner race fault state CHMM, outer race fault state CHMM and rolling element fault state CHMM).
Step 5: Diagnosis: input the dimensionality reduction testing feature vectors into the trained four state CHMMs in step 4 and fault diagnosis results are obtained.
Fig. 5The framework of the proposed method
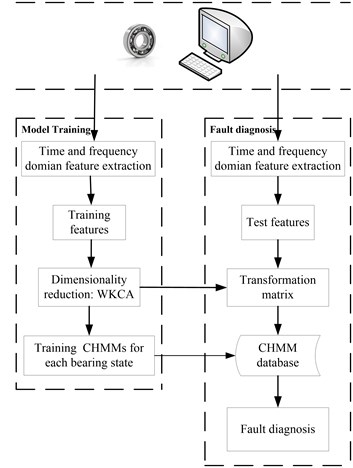
Fig. 6The test rig

The test rig is shown in Fig. 6. The two ends of the shaft are supported by two rolling element bearings, and the right end is detachable which is convenient for replacement of the test rolling element bearings. The shaft is driven by AC motor and connected by coupling. The rated power of the AC is 1.1 kW. The test rig is equipped with hydraulic position and clamping device which are used in fixing the outer race of rolling bearing. The inner race, rolling element and outer race of the test rolling bearings are eroded with very tiny point corrosions respectively using Electrical Discharge Machining (EDM) technology to simulate the three kinds of faults of the rolling bearing. The type of the test rolling bearing is GB203. The outer race is fixed on the bench and the inner race rotates synchronously with the shaft in the test process. The rotation frequency of the shaft is 12 Hz. The parameters and the rotation frequency of the test rolling element bearings are shown in Table 2.
Table 2Rolling bearing’s parameters and the rotating frequency
Type | Pitch diameter (mm) | Ball diameter (mm) | Ball number (N) | Contact angle (angle) |
GB203 | 28.5 | 6.747 | 7 | 0 |
Feature frequency Shaft frequency | Calculation formulas | Calculated result (Hz) 12 | ||
Remark: represent the shaft rotation speed | ||||
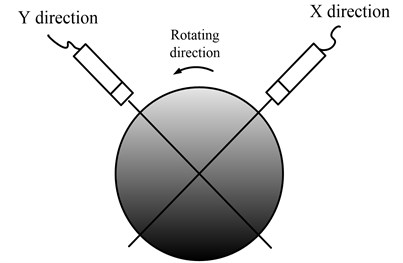
One sensor is installed in the traditional vibration data collection method. In the paper the two accelerometers are installed in the same one bearing case synchronously, and the two installed directions are shown in Fig. 7.
Fig. 7The installation direction of the two sensors
The four states of the test rolling bearings are carried on respectively and the corresponding time-domain waveforms of the two channel signals from the same data collection point of the four states are shown in Fig. 8. The sampling frequency is 25.6 kHz.
It is usually taking on non-gaussian and non-linear characteristic whatever the condition of the rolling bearings is (normal or fault). The time-frequency analysis method is a very effective non-linear and non-gaussian signal handling tool to extract the non-linear features buried in the original signal. In the paper, the wavelet packet energy entropy is used as the time-frequency indicator whose calculation process is shown as following:
Apply the wavelet packet transform (WPT) to the original signal and the energies , is the decomposition level) named wavelet packet energy on each node is obtained which is the division of the original signal in the time-frequency domain. In theory, much better frequency-domain performance could be obtained with the bigger value of . However, the amount of calculation will also be increased with the bigger value of . So, the value of is selected 3 as compromising here, and the satisfactory frequency-domain performance could be obtained with the following verification of experimental results. The wavelet packet energy entropy (WE) is defined as in Eq. (15):
In Eq. (15), represents probability distribution. The Normalized wavelet packet energy and wavelet packet energy entropy results of the signals shown in Fig. 8 are summarized in Fig. 9.
Fig. 8The time-domain waveforms of the two channels signals from the same data collection point of the four states
a) The time-domain waveform of channel 1 of normal state
b) The time-domain waveform of channel 2 of normal state
c) The time-domain waveform of channel 1 of outer race fault state
d) The time-domain waveform of channel 2 of outer race fault state
e) The time-domain waveform of channel 1 of rolling element fault state
f) The time-domain waveform of channel 2 of rolling element fault state
g) The time-domain waveform of channel 1 of inner race fault state
h) The time-domain waveform of channel 2 of inner race fault state
So, the dimensionality of training feature vectors of every channel is 4×50×12. Apply WKPCA to the 4×40×12 feature vectors of channel 1 and 2 respectively and the analysis results are shown in Fig. 10 and Fig. 11. In Fig. 12, the curves of classification result with the number of kernel principle components (PC) is given, and it is evident that the correction ratio would be almost unchanged when the number of PC varies from 3-12. Though in theory the correction ration will obtain the biggest value when the number of PC is selected 12 as shown in Fig. 12, the classification speed will be decreased too much. So, the number is selected 3 as compromising to ensure the classification speed, and the classification correction is guaranteed at the same time. From the dimensionality reduction result it is evident that the dimensionality of the feature vectors is reduced to 4×40×3 respectively.
Fig. 9Normalized wavelet packet energy and wavelet packet energy entropy
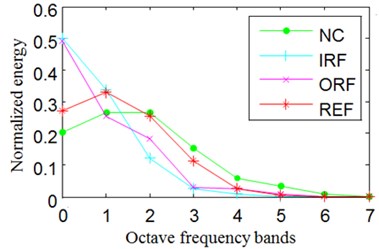
a) The normalized energy of channel 1
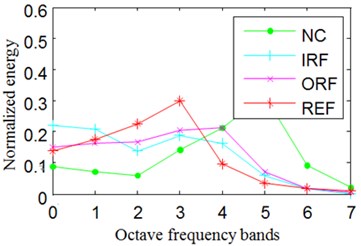
b) The normalized energy of channel 2
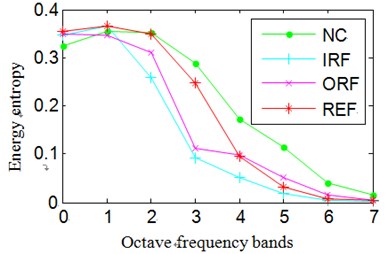
c) The energy entropy of channel 1
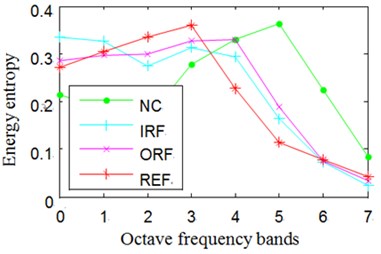
d) The energy entropy of channel 2
Fig. 10The three principle components of the twelve features of the channel 1 of the four states analyzed by WKPCA method
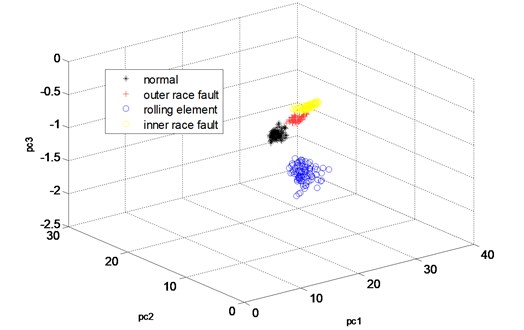
From Fig. 10, it can be seen that, almost all of the four states’ sample vectors (* represents the sample vectors of normal state, + represents the samples vectors of outer race fault state, blue o represents the sample vectors of rolling element fault state and yellow o represents the sample vectors of inner race fault state) are classified correctly. Though small amount of sample vectors of outer race fault state and inner race fault state are misclassified in Fig. 11, most of the other sample vectors of the four states are classified correctly. In order to verify the advantage of WKPCA over KPCA, the analysis result of the signals shown in Fig. 8 using KPCA are given in Fig. 13 and Fig. 14. The advantages of WKPCA over KPCA is obvious compared the Fig. 10 and Fig. 11 with Fig. 13 and Fig.14: Much more amount of sample vectors of the four states are misclassified compared Fig. 13 and Fig. 14 with Fig. 10 and Fig. 11. Besides, the better clustering result which has bigger classes distance and smaller intra-class distance is evident in Fig. 10 and Fig. 11 compared with the results obtained in Fig. 13 and Fig. 14.
Fig. 11The three principle components of the twelve features of the channel 2 of the four states analyzed by WKPCA method
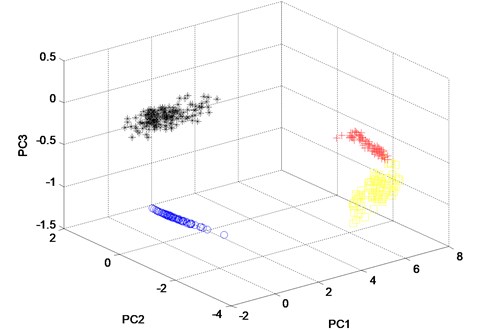
Fig. 12The curves of classification result with the number of kernel principle components
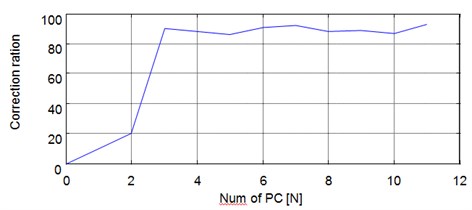
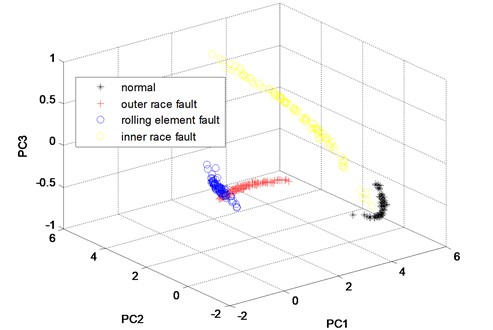
Fig. 13The three principle components of the twelve features of the channel 1 of the four states analyzed by KPCA method
Use the 4×40×3×2 feature vectors as training feature vectors respectively and the normal state CHMM, outer race fault state CMHH, rolling element fault state CHMM and inner race fault state CHMM diagnosis trained models are erected respectively. Then input the 4×40×3×2 feature vectors as testing feature vectors into the above four trained diagnosis models, and the diagnosis results are obtained and shown in Fig. 15(c) at last. From the Fig. 15(c) the ten groups of the testing feature vectors of the four states are classified corrected completely.
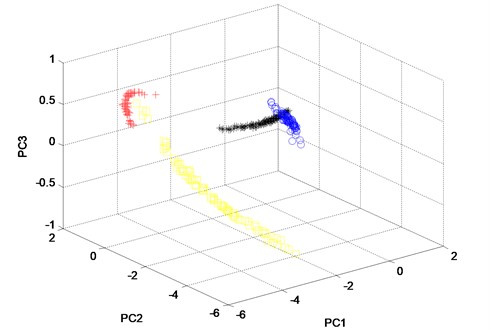
Fig. 14The three principle components of the twelve features of the channel 2 of the four states analyzed by KPCA method
In order to verify the advantage of CHMM over HMM, the diagnosis result based on WKPCA-HMM of the two channel signals of the four states are also carried out respectively. Same as the above CHMM models training and testing process: firstly, use the 4×40×3×2 as training feature vectors respectively and the normal state HMM, outer race fault state MHH, rolling element fault state HMM and inner race fault state HMM diagnosis trained models of the two channel signals are erected respectively, then input the 4×10×3×2 feature vectors as testing feature vectors into the above eight trained diagnosis models, and the diagnosis results are obtained and shown in Fig. 15(a) and Fig. 15(b) respectively. Compared Fig. 15(a) and Fig. 15(b) with Fig. 15(c), the advantages of the proposed method are obvious: in Fig. 15(a) the are three groups of rolling element fault state testing feature vectors are misclassified as normal state. In Fig. 15(b) there is not only one group of rolling element fault state testing feature vector is misclassified as normal state but also there are three groups of outer race fault state testing feature vectors are misclassified as inner race fault state. Based on the above shown results, the advantage of CHMM over HMM in fault diagnosis of rolling element bearing is verified: the CHMM can fuse the information of two channels signals from the same data collection point efficiently and might also resolve the possible coupling phenomenon occurring between the two channel signals synchronously so much more reliable diagnosis result could be obtained compared with the HMM method. Besides, the dimension redundancy and dimension insufficient contraction is not only resolved but also the diagnosis efficiency and correction ratio are also increased because the WKPCA method is used as feature dimensionality method.
Besides, the computation time and correction ratio of the other three relative methods (WKPCA-HMM, RKPCA-CHMM and CHMM without dimensionality reduced) and the proposed method (WKPCA-CHMM) are shown in Table 3. Based on Table 3 the advantages of the proposed are further verified.
Table 3The computation time and correction of the relative methods and the proposed method
The name of methods | Computation time (second) | Correction ratio |
WKPCA-HMM | 34.5 | 70 % |
RKPCA-CHMM | 40.4 | 65 % |
CHMM | 65.3 | 60 % |
WKPCA-CHMM | 38.6 | 100 % |
Fig. 15The diagnosis results based on WKPCA-HMM and WPCA-CHMM
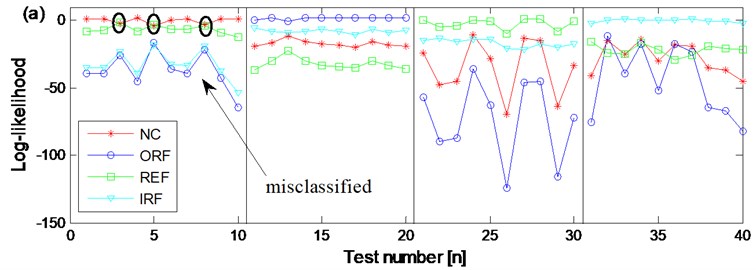
a) The diagnosis results of channel 1 signals of the four states based on WKPCA-HMM
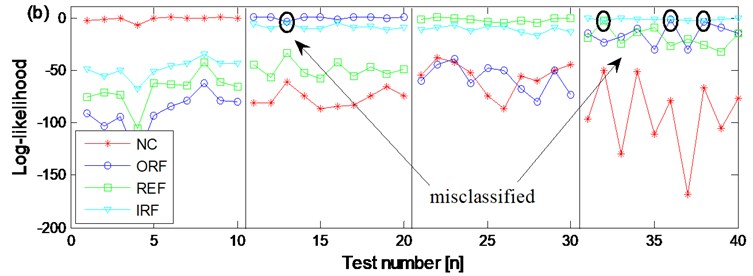
b) The diagnosis results of channel 2 signals of the four states based on WKPCA-HMM
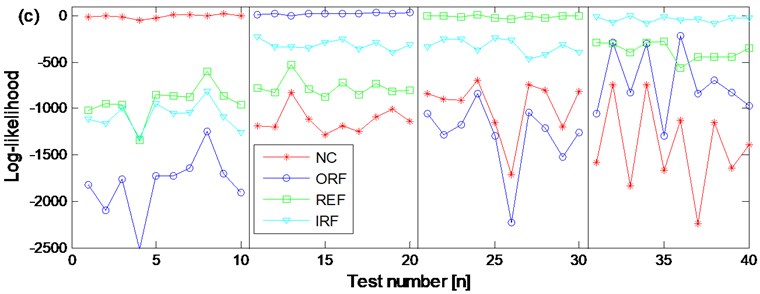
c) The diagnosis results of the two channels signals of the four states based on WKPCA-CHMM
5. Conclusions
The paper presents an integrated WKPCA-CHMM method to realize the intelligent fault diagnosis of rolling element bearing. The advantage of CHMM over HMM is following: the CHMM can fuse the information of two channel signals from the same data collection point efficiently and might also solve the possible coupling phenomenon occurring between the two channel signals synchronously. The WKPCA is used as feature dimensionality reduction method for it is not only can solve the dimension redundancy and dimension insufficient contraction but also is much more flexible than RKPCA. The feasibility and validity of the proposed method is verified through experiment. Besides, the advantages of the proposed method over other relative methods are also verified and presented.
References
-
Jiang R., Yu J., Makis V. Optimal Bayesiam estimation and control scheme for gear shaft fault detection. Computers and Industrial Engineering, Vol. 63, Issue 4, 2012, p. 754-762.
-
Boutros T., Liang M. Detection and diagnosis of bearing and cutting tool faults using hidden Markov models. Mechanical Systems and Signal Processing, Vol. 25, Issue 6, 2011, p. 2102-2124.
-
Geramifard O., Xu J. X., Panda S. K. Fault detection and diagnosis in synchronous motors using hidden Markov model-based semi-nonparametric approach. Engineering Applications of Artificial Intelligence, Vol. 26, Issue 8, 2013, p. 1919-1929.
-
Georgoulas G., Mustafa M. O., Tsoumas I. P. Principal component analysis of the start-up transient and hidden Markov modeling for broken rotor bar fault diagnosis in asynchronous machines. Expert Systems with Application, Vol. 40, Issue 17, 2013, p. 7024-7033.
-
Purushotham V., Narayanan S., Prasad S. A. N. Multi-fault diagnosis of rolling bearing elements using wavelet analysis and hidden Markov model based fault recognition. NDT&E International, Vol. 38, Issue 8, 2005, p. 654-664.
-
Jardine A. K. S., Lin D., Banjevic D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mechanical Systems and Signal Processing, Vol. 20, Issue 7, 2006, p. 1483-1510.
-
Yang B. S., Kim K. J. Application of Dempster-Shafer theory in fault diagnosis of induction motors using vibration and current signals. Mechanical Systems and Signal Processing, Vol. 20, Issue 2, 2006, p. 403-420.
-
Kulkarni S., Bewoor A. Vibration based condition assessment of ball bearing with distributed defect. Journal of Measurements in Engineering, Vol. 4, Issue 8, 2016, p. 87-94.
-
Safizadeh M. S., Latifi S. K. Using multi-sensor data fusion for vibration fault diagnosis of rolling element bearings by accelerometer and load cell. Information Fusion, Vol. 18, Issue 4, 2014, p. 1-8.
-
Brand M., Oliver N., Pentland A. Coupled hidden Markov models for complex action recognition. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, USA, 1997, p. 994-999.
-
Xie L., Liu Z. Q. A coupled HMM approach to video-realistic speech animation. Pattern Recognition, Vol. 40, Issue 8, 2007, p. 2325-2340.
-
Kodali A., Pattipati K. Coupled factorial hidden Markov models (CFHMM) for diagnosing multiple and coupled faults. IEEE Transactions on Systems, Man, and Cybernetics: Systems, Vol. 43, Issue 3, 2013, p. 522-534.
-
Zhao R., Schalk G., Ji Q. Coupled hidden Markov model for electrocorticographic signal classification. 22nd International Conference on Pattern Recognition, 2014, p. 1858-1862.
-
Xiao W. B., Chen J., Dong G. M. A multichannel fusion approach based on coupled hidden Markov models for rolling element bearing fault diagnosis. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 226, Issue 1, 2012, p. 202-216.
-
Liu T., Chen J., Zhou X. N., Xiao W. B. Bearing performance degradation assessment using linear discriminant analysis and coupled HMM. 25th International Congress on Condition Monitoring and Diagnostic Engineering, Journal of Physic: Conference Series, Vol. 364, 2012.
-
Bellino A., Fasana A., Garibaldi L. PCA-based detection of damage in time-varying systems. Mechanical Systems and Signal Processing, Vol. 24, Issue 4, 2010, p. 2250-2260.
-
Xiao Y. Q., Feng L. G. A novel linear ridgelet network approach for analog fault diagnosis using wavelet-based fractal analysis and kernel PCA as preprocessors. Measurement, Vol. 45, Issue 3, 2010, p. 297-310.
-
Cao M. S., Ding Y. J., Ren W. X., Wang Q., Ragulskis M. Hierarchical wavelet-aided neural intelligent identification of structural damage in noisy conditions. Applied Science, Vol. 7, Issue 391, 2017, https://doi.org/10.3390/app7040391
-
Ganey J. L., Block W. M., Jenness J. S. Mexican spotted owl home range and habitat use in pine-oak forest: implications for forest management. Forest Science, Vol. 45, Issue 1, 1999, p. 127-135.
-
Taylor J. S., Cristianini N. Kernel Methods for Pattern Analysis. Cambridge University Press, Cambridge, 2004.
-
Nefian A. V., Liang L. H., Pi X. P. Dynamic Bayesian networks for audio-visual speech recognition. Eurasip Journal on Applied Signal Processing, 2002, https://doi.org/10.1155/S1110865702206083.
-
Zhang L., Zhou W. D., Jiao L. C. Wavelet support vector machine. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 34, Issue 1, 2004, p. 34-39.
-
Smola A. J., Scholkopf B., Muller K. R. The connection between regularization operators and support vector kernels. Neural Networks, Vol. 11, Issue 4, 1998, p. 637-649.
-
Wen X. J., Xu X. M., Cai Y. Z. Least-squares wavelet kernel method for regression estimation. International Conference on Natural Computation 2005, Changsha, 2005, p. 582-591.
Cited by
About this article
The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: the research is supported by the National Natural Science Foundation (China) (approved Rant: 51405453 and 51205371).
