Abstract
The fault diagnosis of motorized spindle contributes to the improvement of the reliability of computer numerical control machine tools. Presently, numerous mechanical fault diagnosis technologies suffer from the drawbacks of mode mixing, non-adaptive analysis, and low efficiency. Therefore, adopting an effective signal processing method for fault diagnosis of motorized spindle is essential. A method based on modified empirical wavelet transform (EWT) and kernel principal component analysis (Kernel PCA) is proposed. A new method, which determines the proper number of the Fourier spectrum segments, is applied when using EWT. To improve computational efficiency, Kernel PCA is adopted to reduce dimension. The support vector machine optimized by genetic algorithm is introduced to accomplish fault identification. The performance of the proposed method is validated through single and compound fault experiments. Results show that the recognition rate using the proposed method reached 98.8095 % and 98.4375 % in terms of single and compound fault diagnoses, respectively. Moreover, compared with empirical mode decomposition (EMD), ensemble empirical mode decomposition (EEMD), local mean decomposition (LMD) and EWT, the proposed method can save much computing time. The proposed method can be generalized to other mechanical fault diagnoses as well.
1. Introduction
High-speed machining is a promising technology that drastically increases productivity and reduces production costs resulting in a revolutionary leap in manufacturing [1, 2]. The motorized spindle is crucial in implementing high-speed machining. And it is popular in manufacturing field because of its advantages, such as zero transmission, small vibration, precise control of rotational acceleration and deceleration [3, 4]. However, owing to the combination of tools and built-in motors, the motorized spindle is much more complex compared with the traditional spindle [5]. The reliability of the motorized spindle remains to be improved mainly due to the complex structure which recently draw attention of industry and academy. This further indicates the importance of seeking methods for the fault diagnosis of the motorized spindle to improve the performance and reliability of computer numerical control (CNC) machine tools.
With the rapid development of signal processing technology, mechanical fault diagnosis technology has been intensively studied. Several approaches for mechanical fault diagnosis, including acoustic emission, oil monitoring, infrared temperature measurement, and vibration analysis, have been reported. Vibration analysis, which is extensively used in condition monitoring and fault diagnosis of mechanical equipment, is the most popular and effective approach [6-9]. The vibration signals of mechanical equipment include a large amount of information which is sensitive to different operation states. Therefore, signal processing techniques, especially in processing vibration signals, attract considerable interest over the past few years. However, using fast Fourier transform (FFT) for fault diagnosis present numerous problems in spectrum analysis, mainly owing to the vibration signals of mechanical equipment are non-linear and non-stationary, meanwhile, these signals are covered by a large scale of noise and closely spaced frequencies [10]. To overcome these limitations, short-time Fourier transform (STFT) [11], Wigner-Ville distribution [12] and wavelet transform [13, 14] are widely applied as the most common time–frequency analysis tools. Some cases yielded desirable results with the use of the aforementioned methods for fault diagnosis. For example, a comparative study of FFT, STFT, and wavelet techniques for induction machine fault diagnostic analysis was performed by Mehala et al. [15]. The experimental results show that STFT and wavelet transform provide better results than FFT and can effectively diagnose shorted turns and broken rotor bars in non-constant load torque induction-motor applications. Although STFT overcomes the shortcomings of FFT-based methods in processing non-linear and non-stationary signal, it cannot achieve low- and high-frequency components analysis simultaneously because its fixed spectral resolution provides the predefined window length, which inadequately describes instantaneous frequency [16-18]. Thus, STFT is suitable for processing quasi stationary signals instead of realistic non-linear and non-stationary signals [13]. Wigner-Ville distribution has a high time and frequency resolution, but its application is restricted in multicomponent signal analysis because of cross-product term interferences [19, 20]. Compared with STFT, wavelet transform is a more effective tool in analyzing non-linear and non-stationary signals because of its property on multi-resolution analysis. Wavelet transform has already achieved good results in condition monitoring and fault diagnosis of mechanical equipment, such as bearing fault [21] and planetary gearbox fault detection [22]. Dyadic wavelet transform is widely used in fault diagnosis of induction motors, rolling bearings, and other rotary machine owing to its high efficiency [23-25]. Unfortunately, as a non-adaptive algorithm, wavelet transform cannot decompose signals according to its contained information [26, 27], and a highly noisy environment immensely influences wavelet transform capability. What’s more, the analysis results using wavelet transform depend on the choice of predefined wavelet basis, which leads to a subjective and a priori assumption on the signal characteristics.
To solve shortages of wavelet, transform, namely non-adaptive and priori assumption, a completely different method named empirical mode decomposition (EMD) was proposed by Huang et al. [28]. EMD gain fruitful achievements in various application fields since its introduction in 1998, such as seismic exploration, fault diagnosis, voice recognition, medicine, and biology. The basic principle of EMD is that practical signals are decomposed into a series of complete and almost orthogonal components called intrinsic mode function (IMF) [26, 28-30]. Each IMF is considered to be a mono-component, which indicates the natural mode contained in the original signal [9, 26]. In comparison with STFT, Wigner-Ville distribution and wavelet transform, EMD is more suitable for analyzing non-linear and non-stationary signals. Nevertheless, EMD is well known for the deficiency in the accurate estimation of instantaneous frequencies [26, 31]. For example, the EMD method cause end effects, and lacks mathematical theory basis, besides, mode mixing is found between IMFs, wherein the IMFs are not strictly orthogonal to each other [26, 32, 33]. Therefore, in order to decrease the effect of mode mixing, an improved version of EMD, namely ensemble empirical mode decomposition (EEMD) is proposed [34]. The EEMD method is applied to rotor fault diagnosis of rotating machinery, and receive satisfactory results [35]. Unfortunately, EEMD loses the advantage of adaptive decomposition, because it is still an open problem for adaptively selecting the amplitude of the added noise and determining the number of ensemble. In addition, many methods have been widely applied in the fault diagnosis of mechanical equipment, such as local mean decomposition (LMD), principal components analysis (PCA), independent components analysis (ICA), and EMD combined with other techniques. A method combining wavelet packet decomposition (WPD) and EMD was adopted to extract fault feature frequency, and a three-layered neural network for rotating machinery early fault diagnosis was proposed [36]. The performance of the proposed method is illustrated through shaft fault experiment with lateral early crack of rotating machinery. For the intelligent fault diagnosis of induction motors, a method combined with ICA and support vector machines (SVM) was applied, and satisfactory results are obtained [37]. The multi-variate and multi-scale monitoring of large-size low-speed bearings using EEMD combined with principal component analysis was executed [38]. The proposed method can accurately identify the local bearing small defects. Han et al. [39] adopted LMD combined with sample entropy and energy ratio to process the vibration signals of roller bearings, and then, different operation states can be classified using SVM. Du et al. [40] presented a method based on the combination of LMD, energy moment, and directed acyclic graph SVM to perform the fault diagnosis of rotating machines of rail vehicles. Liu et al. [41] applied EMD combined with Hilbert spectrum to analyze the working condition of gearbox, and the proposed method exhibited excellent performance. However, the above references mainly deal with single fault diagnosis, compound fault diagnosis is not considered.
Feature extraction and state recognition are cores in the fault diagnosis of mechanical equipment, and the vibration signals collected from mechanical equipment are non-linear and non-stationary in general cases. Adopting powerful signal process tools benefits the revelation of fault characteristics. Considering the characteristic of EMD, EEMD and wavelet transform, a new method named empirical wavelet transform (EWT) was introduced by Gilles [42]. The main principle of this method is the extraction of amplitude modulated-frequency modulated (AM-FM) components from the original signal by building a set of suitable wavelet filters, which are equivalent to segmentation of the Fourier spectrum. However, EWT performance is degraded under substantial noise. Therefore, signal preprocessing is necessary to increase signal-to-noise ratio (SNR). A comparative study on wavelet threshold de-noising for rolling bearing fault research was performed [43], which investigated the performance of wavelet transform modulus local maxima de-noising and wavelet threshold de-noising through acoustic emission signal [44]. Satisfactory results were obtained using penalty wavelet threshold de-noising. Another problem with respect to the segmentation of the Fourier spectrum should be seriously considered. Operational modal analysis (OMA) [45] and multiple signal classification [46] were used to determine the support boundaries of the filter applying EWT for processing non-linear and non-stationary signals, and the efficiency was validated. In addition, a comparative study on PCA, ICA, and Kernel PCA for dimensionality reduction in SVM [47] revealed that feature extraction can improve the generalization performance of support vector machine (SVM), and the best performance was obtained by Kernel PCA.
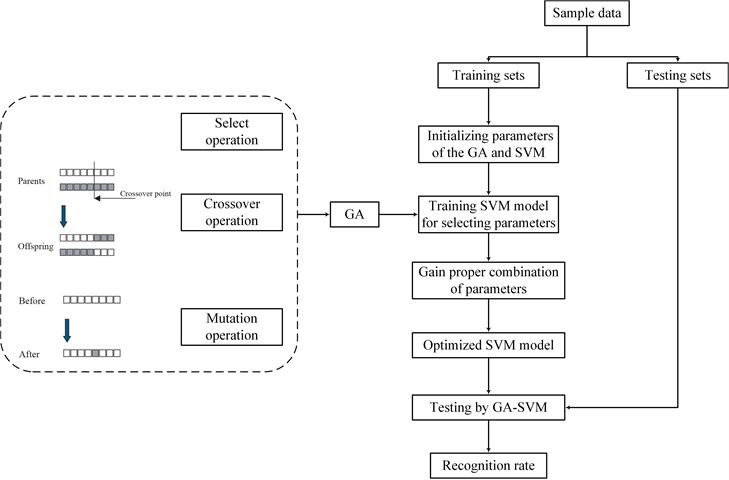
In this paper, a method combining modified EWT with Kernel PCA is applied in the single and compound fault diagnosis of the motorized spindle. Penalty wavelet threshold de-noising is adopted for data preprocessing before executing EWT, and a new approach is proposed to determine the number of the Fourier spectrum segment when using EWT. The SVM optimized by genetic algorithm (GA-SVM) is used as the multi-fault classifier because the SVM from statistical learning theory has better generalization property than conventional pattern recognition [48]. The performance of the proposed method is validated through single and compound fault experiments in a motorized spindle and is better compared with that of EMD, EEMD, LMD and EWT with proper number of segments. The flow chart of the present scheme is presented in Fig. 1.
Fig. 1Flow chart of the present scheme
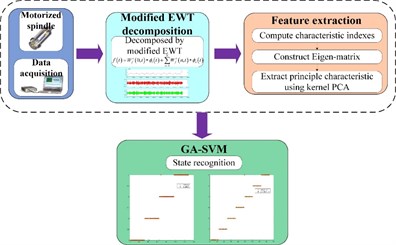
The paper is arranged as follows: Section 2 briefly introduces the theoretical background of EWT, Kernel PCA, and SVM, and a new approach to decide the number of the Fourier spectrum segment when using EWT is also proposed. In Section 3, the data acquisition of single and compound faults in a motorized spindle is described in detail. Section 4 presents the data processing and experimental results. Moreover, a comparative study among modified EWT-Kernel PCA, EMD, EEMD, LMD and EWT (the proper number of segment is selected) is executed. Finally, conclusions are drawn in Section 5.
2. Methodology
2.1. Modified empirical wavelet transform
2.1.1. Empirical wavelet transform
EWT is a self –adaptive algorithm appropriate for processing non-linear and non-stationary signals by designing a series of bandpass filters. The self-adaptive property mainly embodies the support of filters depends on where the information embedded in the analyzed signal is situated. Signal modes are extracted by EWT, which are AM-FM components that have compact support to the Fourier spectrum [49]. Assuming that the Fourier spectrum (frequency ) is partitioned into consecutive segments, which correspond to different modes, is defined as the limit between each segment (where and ), and the transition phase, which exists centered around each , is denoted as of width . A proportional relationship between and exists, namely , where . The idea used in the construction of both Littlewood-Paley and Meyer’s wavelets is applied on the creation of empirical wavelets. For , the empirical scaling function and the empirical wavelets are given by the following equations:
To obtain a tight frame, parameter satisfies following condition:
The function is an arbitrary function, such that:
Numerous functions satisfy these properties, and the following function is frequently used [50]:
Similar to wavelet transform, EWT is denoted as . Its detail coefficients are defined by the inner products of raw signals and the empirical wavelets, shown in the following equation:
The approximation coefficients are acquired by the inner products of raw signals and the scaling function as in the following equation:
The reconstruction and the empirical mode are obtained by:
where is the signal, is the time, and is the time variable.
2.1.2. Determine the number of the Fourier spectrum segment
In order to find the limits between each segment, the method that computes the local maxima and then the boundaries are set as the smallest minima between consecutive maxima is adopted in this paper. However, the number of segments of the Fourier spectrum is difficult to determine because of lacking priori information for practical analysis. Excessive or less segment contradicts the effect of fault diagnosis. Therefore, determining the proper number of segments is crucial.
Fig. 2Framework of the proposed method
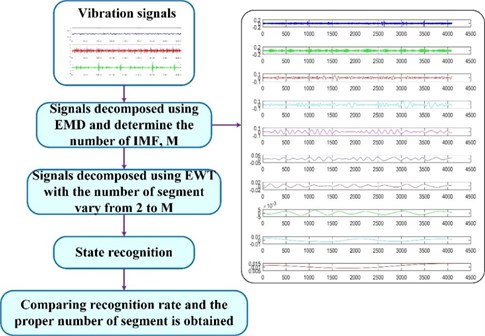
EMD is well known in suffering from mode mixing. The proper number of the Fourier spectrum segment is believed to be less than the number of IMF using EMD in this paper, and the IMF number is denoted as . Afterwards, the proper number of segments is easily determined by comparing the recognition rate of the fault diagnosis using GA-SVM with the number of segment vary from 2 to . The framework of the proposed method for determining the optimal number of EWT segments is shown in Fig. 2.
2.2. Kernel principal component analysis (Kernel PCA)
Although PCA can perform well in processing a set of linear data, it is not applicable for non-linear data. To deal with non-linear data, the extended version of PCA, KPCA, is introduced [51]. By using the kernel method, the non-linear data can be mapped into a higher dimensional space in which they vary linearly. Given a set of centered data , , , then these centered data are mapped into a higher dimensional feature space by non-linear mapping . Covariance matrix is computed in as:
The eigenvalues and eigenvectors satisfy the following equation:
All solutions with lie in the span of . Hence, the following equation is obtained:
where is the coefficient. According to Eq. (12), we can obtain:
The kernel trick is applied, and is the kernel matrix. We can obtain:
where is the column vector with entries . To find the solutions of Eq. (14), we solve the eigenvalue problem:
Define as the eigenvalues of , , which are the corresponding complete set of eigenvectors, and is the first non-zero eigenvalue. According to a specific requirement, normalization processing in feature space is executed for the corresponding eigenvectors where:
By synthesizing Eq. (12) and Eq. (15), the following equation is obtained:
Computation of the projections onto the eigenvectors in is necessary to extract the principal component:
In addition, the problem on selecting the proper number of principal components has attracted considerable interests for the past decade. A series of criteria have been adopted in the selection of the number of principal components, and the most frequently used approach, that is, cumulative contribution limit [52], is applied in this paper.
2.3. Support vector machine optimized by genetic algorithm
SVM was first proposed by Vapnik et al. based on statistical learning theory [48]. Through time, SVM become increasingly popular in machine learning, and has been widely used in machine fault diagnosis because of its better generalization and higher recognition rate for analysis of small set of samples compared to traditional pattern recognition approaches such as artificial neural networks (ANN). The basic principle of SVM for typical two-class classification problems is described as follows. Given a set of training data , and , SVM aims to find a high dimensional space in which the training data can be separated by the hyperplane as accurately as possible. In the linear separable case, the hyperplane can be expressed in the following equation:
where is the -dimensional vector, is the input vector, and is the scalar.
The training data are classified into two portions, and they are referred as negative and positive objects by hyperplane. The positive and negative object labels are and , respectively. An optimal separating hyperplane, which creates the maximum distance between two edge lines, depended on support vectors. A linear classification is shown in Fig. 3. The slack variables and the penalty parameter are introduced because of considering the noise. Thus, the optimal problem can be expressed as:
where is the Euclidean norm of .
Kernel transform is applied when the original data should be mapped into a higher feature space facing the non-linear problem, and is the kernel function. The SVM classifier output is then expressed as:
where is the Lagrange multipliers and is the support vector.
Fig. 3Linear classification
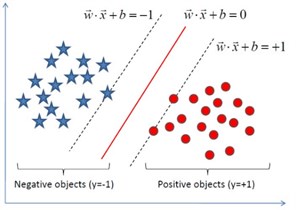
Radial basis function is a common kernel function, and it has been used as kernel of SVM in numerous articles. Hence, it is chosen as the kernel function in this study. The radial basis function is defined as follows:
In which is the kernel parameter and is the width parameter of the radical basis function.
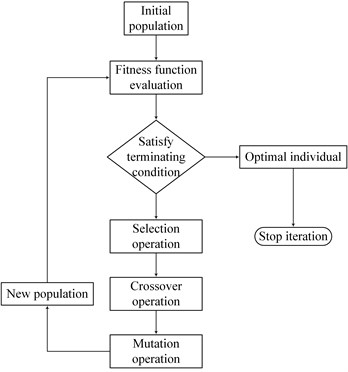
It is essential to select a proper combination of parameters for achieving best prediction accuracy in SVM. It is well known that the GA is a global optimization algorithm based on Charles Darwin’s theory of natural selection and evolution, and it is a powerful tool to solve the optimization problem. Therefore, in order to find the best parameter combination, the GA [53] is applied into SVM. The steps of a simple GA are shown in Fig. 4. In this paper, population size, the number of iterations, crossover probability and mutation probability are set to 20, 200, 0.9 and 0.05, respectively. GA is introduced to find a proper combination of parameters, namely and , and the value ranges are both set to the range of 0 to 200. In addition, the SVM recognition rate serves as the fitness function. The flowchart of GA-SVM is presented in Fig. 5.
Fig. 4Genetic algorithm flowchart
3. Data acquisition of single and compound faults
According to the statistical analysis, bearing fault contributes the largest proportion, accounting for 44.4 %, in the mechanical spindle of machining center [54]. Thus, execution of bearing fault diagnosis of the motorized spindle is necessary. In addition, rotor unbalance and bolt looseness fault immensely impact the performance of motorized spindle. To verify the effectiveness of the proposed method, the bearing fault data, which comes from the bearing data center of Case Western Reserve University was utilized for single fault diagnosis [55]. As for the compound fault diagnosis, vibration data was acquired in different fault conditions, namely normal, rotor unbalance, bolt looseness, and compound fault (rotor unbalance and bolt looseness coexist).
Fig. 5Flowchart for GA-SVM
3.1. Data acquisition of single faults
Experiments for bearing single faults were conducted in a test stand. The test stand is composed of a three-phase induction motor, an AC electrical dynamometer, a torque sensor, and a control system. The 6205-2RS JEM SKF, deep groove ball bearing, was selected as test bearing, which supports the induction motor shaft. The localized defects were created on the inner and outer raceways and the ball by utilizing electro-discharge machining. The diameters of single point faults were 0.1778 and 0.3556 mm, and the depth of defect was consistent at 0.2794 mm. Accelerometers were used to acquire vibration signals, which were fixed in the drive end of the induction motor housing with magnetic bases, in which the laying position was at the 6 o’clock position. The vibration signals were acquired at a sampling frequency of 12000 Hz, and the motor output speed was 1772 rpm with 1 horsepower motor load.
3.2. Data acquisition of compound faults
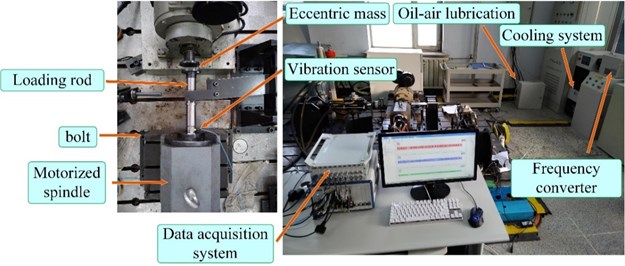
Compound fault experiments in a motorized spindle were conducted in the test platform as shown in Fig. 6.
The test platform consists of a data acquisition system, oil-air lubrication, cooling system, frequency converter, loading rod, and a motorized spindle. The loading rod was installed in the motorized spindle, and the eccentric mass was fixed in the loading rod, which realizes the fault simulation for rotor unbalance. In addition, the motorized spindle was fixed by four bolts, and three of them were loosened when the bolt looseness fault experiment was conducted. Considering safety, the speed of the motorized spindle was set to 5000 rpm. Vibration signals were collected in various states at a sampling frequency of 5000 Hz. Electromagnetic interference should be given attention because of the frequency converter. Therefore, vibration signals were preprocessed using Penalty wavelet threshold de-noising, which can increase SNR.
Fig. 6Test platform of the motorized spindle
4. Data processing and experimental results
4.1. Single fault diagnosis
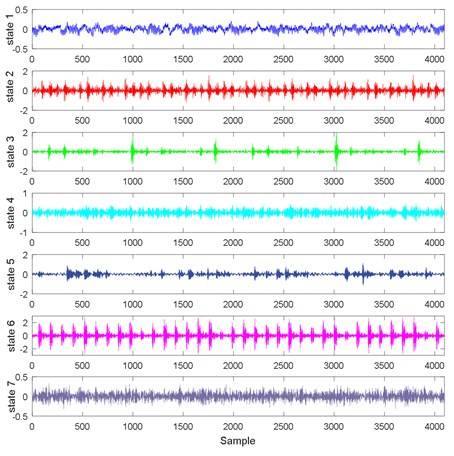
In the experiment of single faults, vibration signals are collected in seven states, namely the normal condition, the inner raceway fault (two states with different fault diameters), the ball fault (two states with different fault diameters), and the outer raceway fault (two states with different fault diameters). The fault diameters are 0.1778 mm and 0.3556 mm respectively. The time domain waveforms of vibration signals collected in seven states are presented in Fig. 7. Single fault diagnosis aims to identify the seven states effectively and accurately. Vibration signals collected in a certain state are divided into 29 subsets with equal lengths of 4096. A detailed description for vibration signals is shown in Table 1.
Fig. 7Time domain waveforms of vibration signals
The EWT-Kernel PCA method is applied to process vibration signals. To start with, the proper number of segment needs to be determined. EMD is initially applied to analyze vibration signals, and the number of intrinsic mode function obtained using EMD is between 10 and 12. Considering that EMD suffers from the major shortcoming of mode mixing, the determination of the proper number of segment is reasonably not larger than 10. Vibration signals collected at different states are then decomposed using EWT, and the number of segment varies from 2 to 10. Energy, kurtosis, and root mean square are selected as characteristic indexes. Characteristic indexes of the signals, which are decomposed by using EWT, are extracted to construct Eigen-matrix which serves as input of GA-SVM. The recognition rate is obtained using GA-SVM, and the results are presented in Table 2. The proper number of segment is determined by comparing the recognition rate.
Table 1Detailed description of vibration signals
Class | Bearing fault | Defect size (mm) | Sample number |
State 1 | Normal | 0 | 29 |
State 2 | Inner raceway | 0.1778 | 29 |
State 3 | Inner raceway | 0.3556 | 29 |
State 4 | Ball | 0.1778 | 29 |
State 5 | Ball | 0.3556 | 29 |
State 6 | Outer raceway | 0.1778 | 29 |
State 7 | Outer raceway | 0.3556 | 29 |
Table 2Recognition rate (single faults)
Number of segment | Recognition rate (%) | Time (s) |
2 | 98.8095 | 24.0550 |
3 | 100 | 25.9561 |
4 | 97.6190 | 26.9161 |
5 | 95.2381 | 27.7974 |
6 | 95.2381 | 32.0490 |
7 | 95.2381 | 32.1671 |
8 | 96.4286 | 32.5506 |
9 | 94.0476 | 33.2683 |
10 | 94.0476 | 33.7320 |
According to Table 2, the highest recognition rate is easily found when the number of segment varies from 2 to 10. From Table 2, we can see that the highest recognition rate is 100 % when the number of segment is 3; therefore, the proper number of segment is 3. Kernel PCA is applied to extract the principal characteristics from Eigen-matrix. Furthermore, cumulative contribution limit is adopted to determine the number of principal characteristics. The detailed description for cumulative contribution is presented in Table 3.
Table 3Cumulative contribution
Serial number | Eigenvalue | Cumulative contribution |
1 | 124.6073 | 0.6412 |
2 | 24.2019 | 0.7657 |
3 | 16.1617 | 0.8489 |
4 | 9.6115 | 0.8984 |
5 | 7.7455 | 0.9382 |
6 | 4.9167 | 0.9635 |
7 | 3.0010 | 0.9790 |
8 | 2.6911 | 0.9928 |
9 | 1.3953 | 1 |
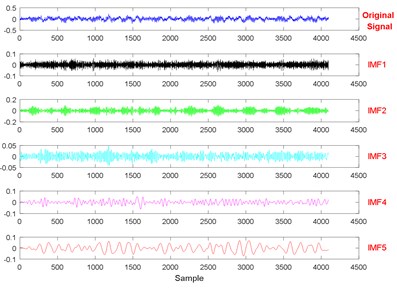
The threshold of cumulative contribution limit is set to 0.90 in this paper. According to Table 3, the anterior five characteristics are extracted as principal characteristics. Finally, the new Eigen-matrix serves as the input of GA-SVM. Table 1 shows that a total of 29 samples are obtained in each state, and the anterior 60 % of samples are selected as training samples. For comparison, EMD, EEMD and LMD are applied to decompose vibration signals collected in different states as well. When using EEMD, there are two parameters are needed to be set, which are the ensemble number and the amplitude of the added white noise. In this study, the ensemble number and the amplitude of the added white noise are set to 100 and 0.2, respectively [56]. The results of EEMD/EWT/LMD decomposition are given in Figs. 8-13. In this paper, we only give the results of two states, namely State 1 (Normal) and State 7 (Outer raceway fault, the defect size is 0.3556 mm) because of limited space. Then energy, kurtosis, and root mean square are computed to construct an Eigen-matrix, which is inputted in GA-SVM, and the result is shown in Figs. 14-17. A detailed comparison results for single fault diagnosis is presented in Table 4. According to Table 4, modified EWT-Kernel PCA, EWT ( 3), EEMD and LMD are superior to EMD in two aspects: recognition rate and computing time. In addition, modified EWT–Kernel PCA, EWT ( 3), EEMD and LMD can reach a high recognition rate. As for computing time, the modified EWT-Kernel PCA is better than EWT ( 3), EEMD and LMD.
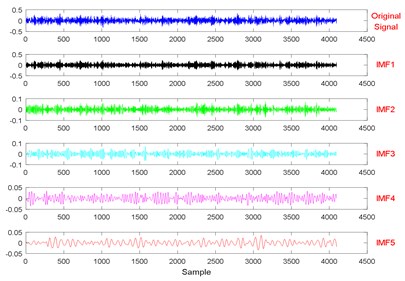
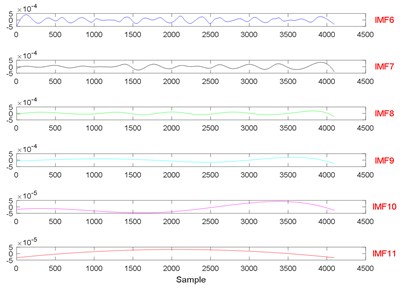
Fig. 8The signal decomposition of State 1 by EEMD
a)
b)
Fig. 9The signal decomposition of State 7 by EEMD
a)
b)
Fig. 10The signal decomposition of State 1 by EWT
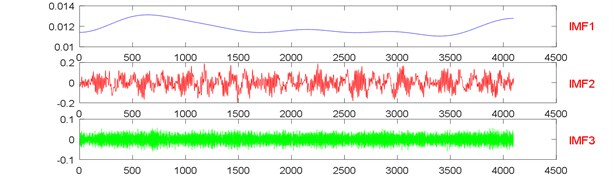
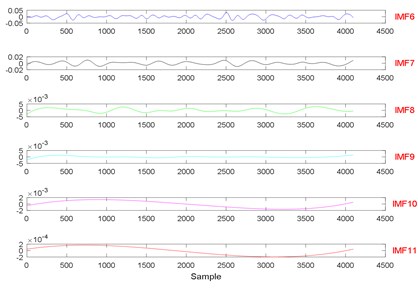
Fig. 11The signal decomposition of State 7 by EWT
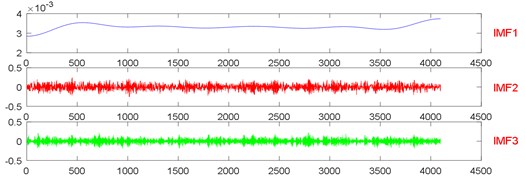
Fig. 12The signal decomposition of State 1 by LMD
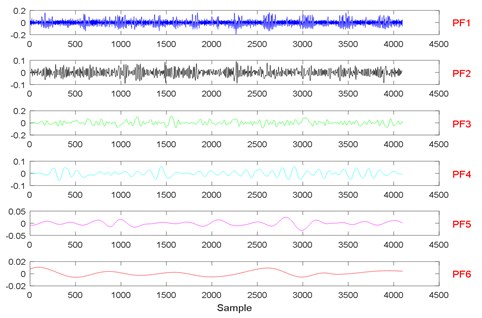
Fig. 13The signal decomposition of State 7 by LMD
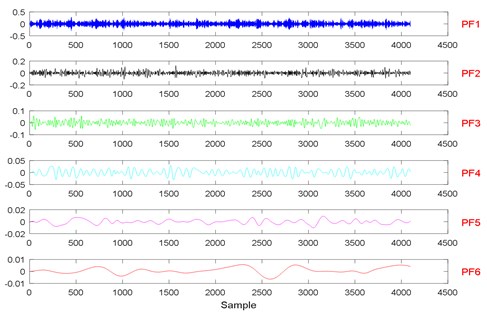
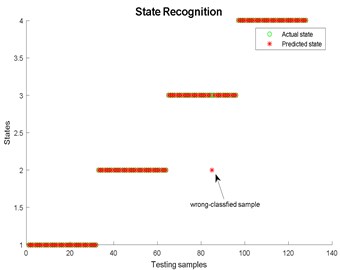
Fig. 14State recognition using the modified EWT-Kernel PCA
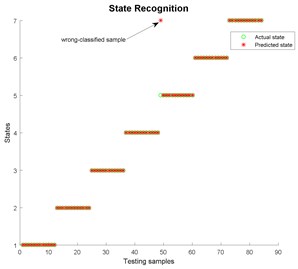
Fig. 15State recognition using EMD
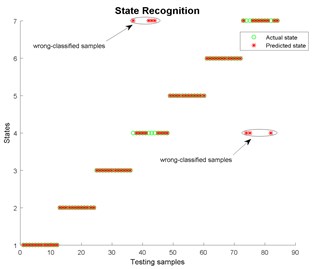
Fig. 16State recognition using EEMD
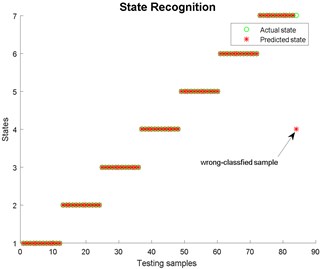
Fig. 17State recognition using LMD
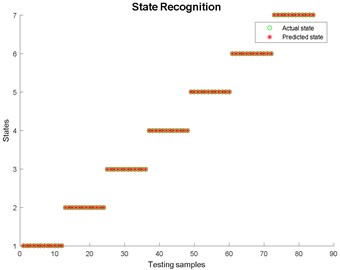
Table 4Comparison results (single fault diagnosis)
Method | Recognition rate (%) | Time (s) | Optimum parameters | |
Modified EWT-Kernel PCA | 98.8095 | 20.8028 | 2.9676 | 18.6115 |
EWT ( 3) | 100 | 25.9561 | 21.5076 | 1.9846 |
EMD | 91.6667 | 32.4293 | 3.2776 | 0.7719 |
EEMD | 98.8095 | 27.3467 | 13.4472 | 0.4829 |
LMD | 100 | 27.9825 | 6.8211 | 1.0040 |
4.2. Compound fault diagnosis
In the compound fault experiment, vibration signals are collected in four states, namely normal, rotor unbalance, bolt looseness, and compound fault (rotor unbalance and bolt looseness coexist). The time domain waveforms of vibration signals, which are preprocessed using Penalty wavelet threshold de-noising, are presented in Fig. 18.
To identify the four states effectively and accurately, the preprocessed vibration signals are segmented into 80 subsets of equal lengths of 4096. Further description is presented in Table 5.
Fig. 18Time domain waveform of vibration signals
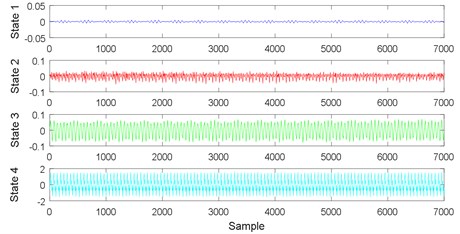
Table 5Further description of the preprocessed vibration signals
Class | Fault | Sample number |
State 1 | Normal | 80 |
State 2 | Bolt looseness | 80 |
State 3 | Rotor unbalance | 80 |
State 4 | Compound fault | 80 |
The processing procedures of compound fault diagnosis are the same as that of single fault diagnosis. EMD is initially utilized to analyze vibration signals, and the number of intrinsic mode function obtained using EMD is between 9 and 11. The proper number of segment is considered less than 9 because EMD suffers from mode mixing. Vibration signals collected in four states are then decomposed using EWT, and the number of segment varies from 2 to 9. Energy, kurtosis and root mean square are extracted to construct Eigen-matrix, which serves as the input of GA-SVM. The results are presented in Table 6. The comparison results of the recognition rates of compound fault diagnosis revealed that the proper number of segment can be found.
Table 6Recognition rate (compound faults)
Number of segment | Recognition rate (%) | Time (s) |
2 | 49.2188 | 24.6227 |
3 | 75.7813 | 26.6460 |
4 | 88.2813 | 26.4702 |
5 | 97.6563 | 25.1563 |
6 | 78.1250 | 27.3122 |
7 | 95.3125 | 24.1459 |
8 | 96.0938 | 26.7265 |
9 | 81.2500 | 28.1158 |
Table 6 shows that the highest recognition rate is obtained when the number of segment varies from 2 to 9. Hence, the proper number of segment is 5. Kernel PCA is applied to extract principal characteristics from Eigen-matrix. Cumulative contribution limit is adopted to determine the number of principal characteristics. The detailed description for cumulative contribution is presented in Table 7.
Table 7Cumulative contribution
Serial number | Eigenvalue | Cumulative contribution |
1 | 119.2375 | 0.5610 |
2 | 14.9248 | 0.6312 |
3 | 14.0555 | 0.6973 |
4 | 11.8911 | 0.7533 |
5 | 9.2964 | 0.7970 |
6 | 7.0838 | 0.8303 |
7 | 6.5162 | 0.8610 |
8 | 5.6663 | 0.8877 |
9 | 4.9138 | 0.9108 |
10 | 4.3771 | 0.9314 |
11 | 3.9011 | 0.9497 |
12 | 2.9933 | 0.9638 |
13 | 2.7913 | 0.9769 |
14 | 2.5411 | 0.9889 |
15 | 2.3607 | 1 |
According to Table 7, because the threshold of the cumulative contribution limit is set to 0.90 in this paper, the anterior nine characteristics are extracted as principal characteristics. Finally, the new Eigen-matrix serves as the input of GA-SVM. Based on Table 5, a total of 80 samples are obtained in each state, and the anterior 60 % of samples are selected as training samples. The results of EEMD/EWT/LMD decomposition are given in Figs. 19-24. In this paper, we only give the results of two states, namely State 1 (Normal) and State 4 (Compound fault) because of limited space. The results of state recognition using modified EWT-Kernel PCA, EMD, EEMD and LMD are shown in Figs. 25-28. The result of the detailed comparison of compound fault diagnosis is presented in Table 8. According to Table 8, modified EWT-Kernel PCA, EWT ( 5) EEMD and LMD are obviously far superior to EMD in terms of recognition rate. For computing time, the modified EWT-Kernel PCA is better than EWT ( 5), EMD, EEMD and LMD.
Table 8Comparison results (compound faults diagnosis)
Method | Recognition rate (%) | Time (s) | Optimum parameters | |
Modified EWT-Kernel PCA | 98.4375 | 18.0463 | 104.7613 | 1.5739 |
EWT ( 5) | 97.6563 | 25.1563 | 87.7794 | 1.8892 |
EMD | 94.5313 | 43.0471 | 46.9961 | 0.9804 |
EEMD | 99.2188 | 43.5325 | 100.1085 | 0.8619 |
LMD | 99.2188 | 20.2320 | 9.3590 | 0.5783 |
Fig. 19The signal decomposition of State 1 by EEMD
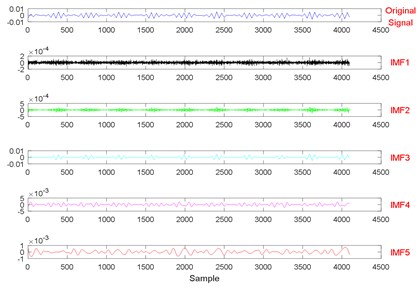
a)
b)
Fig. 20The signal decomposition of State 4 by EEMD
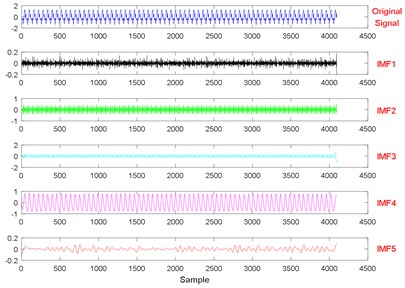
a)
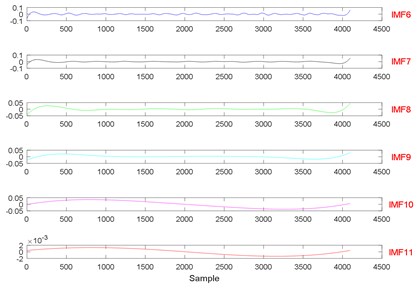
b)
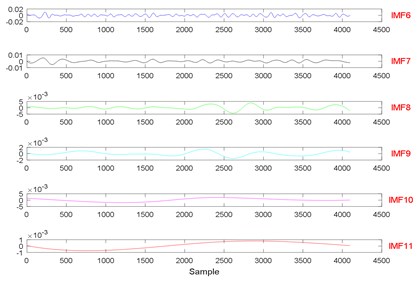
Fig. 21The signal decomposition of State 1 by EWT
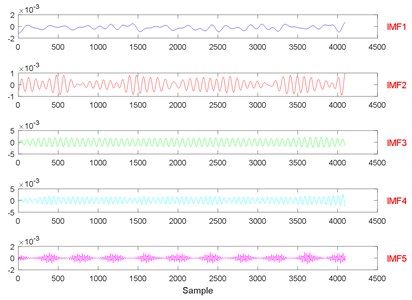
Fig. 22The signal decomposition of State 4 by EWT
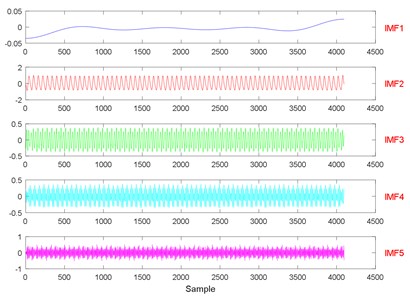
Fig. 23The signal decomposition of State 1 by LMD
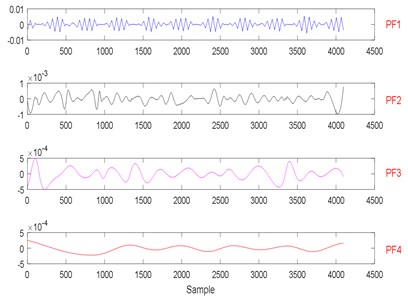
Fig. 24The signal decomposition of State 4 by LMD
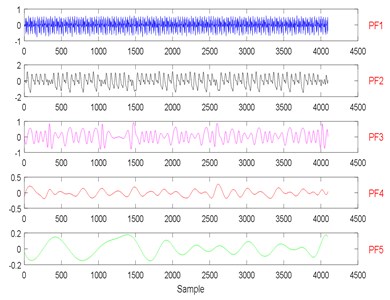
Fig. 25State recognition using modified EWT-Kernel PCA
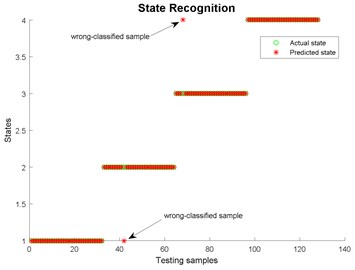
Fig. 26State recognition using EMD
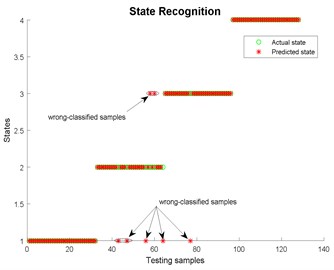
Fig. 27State recognition using EEMD
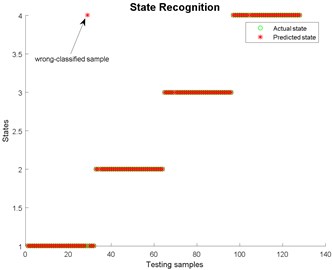
Fig. 28State recognition using LMD
5. Conclusions
In this paper, a method based on modified EWT and Kernel PCA for the single and compound fault diagnoses of the motorized spindle is investigated. A comparison study among EWT (the proper number of segment is selected), EMD, EEMD, LMD and modified EWT-Kernel PCA is executed. The experimental data obtained from the bearing data center of Case Western Reserve University are utilized for the single fault diagnosis of a motorized spindle, and as for compound fault diagnosis, experiments are carried out on a test platform for a motorized spindle. The analysis results indicate that the proposed method can effectively and correctly performs fault diagnosis. The recognition rate using modified EWT-Kernel PCA reach 98.8095 % and 98.4375 % in terms of single and compound fault diagnoses, respectively, which are higher than those in EMD. Moreover, for single fault diagnosis, the recognition rate using modified EWT-Kernel PCA, EWT, EEMD and LMD are almost the same, and as for compound fault diagnosis, modified EWT-Kernel PCA, EEMD and LMD are superior to EWT ( 5) and EMD. Compared with EWT, EMD, EEMD and LMD in the aspect of computing time, the proposed method saved 19 %, 35 %, 24 % and 26 % for single fault diagnosis, respectively. For compound fault diagnosis, the proposed method saved 39 %, 58 %, 59 % and 11 %, respectively. Finally, this method can be generalized for another mechanical fault diagnosis.
References
-
Bossmanns B., Tu J. F. A thermal model for high speed motorized spindles. International Journal of Machine Tools and Manufacture, Vol. 39, Issue 9, 1999, p. 1345-1366.
-
Wu Y. H. Motorized Spindle Unit Technology of CNC Machine Tools. China Machine Press, Beijing, 2006.
-
Abele E., Altintas Y., Brecher C. Machine tool spindle units. CIRP Annals – Manufacturing Technology, Vol. 59, Issue 2, 2010, p. 781-802.
-
Shan W. T., Chen X. A., He Y., Zhou J. M. A novel experimental research on vibration characteristics of the running high-speed motorized spindles. Journal of Mechanical Science and Technology, Vol. 27, Issue 8, 2013, p. 2245-2252.
-
Liu J. F., Chen X. A. Dynamic design for motorized spindles based on an integrated model. The International Journal of Advanced Manufacturing Technology, Vol. 71, Issue 9, 2014, p. 1961-1974.
-
Marquez F. P. G., Tobias A. M., Perez J. M. P., Papaelias M. Condition monitoring of wind turbines: techniques and methods. Renew Energy, Vol. 46, 2012, p. 169-178.
-
Yang W. X., Little C., Court R. An online technique for condition monitoring the induction generators used in wind and marine turbines. Mechanical Systems and Signal Processing, Vol. 38, Issue 1, 2013, p. 103-112.
-
Yang W. X., Little C., Court R. S-Transform and its contribution to wind turbine condition monitoring. Renew Energy, Vol. 62, 2014, p. 137-146.
-
Cao H. R., Fan F., Zhou K., He Z. J. Wheel-bearing fault diagnosis of trains using empirical wavelet transform. Measurement, Vol. 82, 2016, p. 439-449.
-
Amezquita-Sanchez J. P., Adeli H. A new music-empirical wavelet transform methodology for time-frequency analysis of noisy nonlinear and non-stationary signals. Digital Signal Process, Vol. 45, 2015, p. 55-68.
-
Allen J. B. Short term spectral analysis, synthesis, and modification by discrete Fourier transform. IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 25, Issue 3, 1977, p. 235-238.
-
Baydar N., Ball Andrew A comparative study of acoustic and vibration signals in detection of gear failures using Wigner-Ville distribution. Mechanical Systems and Signal Process, Vol. 15, Issue 6, 2001, p. 1091-1107.
-
Peng Z. K., Chu F. L. Application of the wavelet transform in machine condition monitoring and fault diagnostics: a review with bibliography. Mechanical Systems and Signal Process, Vol. 18, Issue 2, 2004, p. 199-221.
-
Yu B., Jia L., Ji C., Lin S., Yun L. Trains trouble shooting based on wavelet analysis and joint selection feature classifier. Journal of Multimedia, Vol. 9, Issue 2, 2014, p. 207-215.
-
Mehala N., Dahiya R. A Comparative study of FFT, STFT and wavelet techniques for induction machine fault diagnostic analysis. Proceedings of the 7th Wseas International Conference on Computational Intelligence, Man-Machine Systems and Cybernetics, 2008, p. 203-208.
-
Valtierra-Rodriguez M., Romero-Troncoso R. J., Osornio-Rios R. A., Garcia-Perez A. Detection and classification of single and combined power quality disturbances using neural networks. IEEE Transactions on Industrial Electronics, Vol. 61, Issue 5, 2013, p. 2473-2482.
-
Mallat S. G. A Wavelet Tour of Signal Processing: The Sparse Way. Elsevier/Academic Press, Amsterdam, 2009.
-
Zhang Y. Signals’ Time-Frequency Analysis and Its Application. Harbin Institute of Technology Press, Harbin, 2006.
-
Xiang L., Tang G. J., Hu A. J. Vibration signals’ time-frequency analysis and comparison for a rotating machinery. Journal of Vibration and shock, Vol. 29, Issue 2, 2010, p. 42-45.
-
Spanos P. D. A., Giaralis N., Politis P. Time-frequency representation of earthquake accelerograms and inelastic structural response records using the adaptive chirplet decomposition and empirical mode decomposition. Soil Dynamics and Earthquake Engineering, Vol. 27, Issue 7, 2007, p. 675-689.
-
Li Z., He Z. J., Zi Y. Y., Wang Y. Customized wavelet denoising using intra-and inter-scale dependency for bearing fault detection. Journal of Sound and Vibration, Vol. 313, Issues 1-2, 2008, p. 342-359.
-
Sun H. L., Zi Y. Y., He Z. J., Yuan J., Wang X. D., Chen L. Customized multiwavelets for planetary gearbox fault detection based on vibration sensor signals. Sensor, Vol. 13, Issue 1, 2013, p. 1183-1209.
-
Ebrahimi B. M., Faiz J., Lotfi-Fard S., Pillay P. Novel indices for broken rotor bars fault diagnosis in induction motors using wavelet transform. Mechanical Systems and Signal Processing, Vol. 30, 2012, p. 131-145.
-
Yan R. Q., Gao R. X., Chen X. F. Wavelets for fault diagnosis of rotary machines: a review with applications. Signal Processing, Vol. 96, 2014, p. 1-15.
-
Djebala A., Ouelaa N., Hamzaoui N. Detection of rolling bearing defects using discrete wavelet analysis. Meccanica, Vol. 43, Issue 3, 2008, p. 339-348.
-
Lei Y. G., Lin J., He Z. J., Zuo M. J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mechanical Systems and Signal Processing, Vol. 35, Issues 1-2, 2013, p. 108-126.
-
Yeh P. L., Liu P. L. Application of the wavelet transform and the enhanced Fourier spectrum in the impact echo test. NDT&E International, Vol. 41, Issue 5, 2008, p. 382-394.
-
Huang N. E., Shen Z., Long S. R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of Mathematical, Physical and Engineering Sciences, Vol. 454, Issue 1971, 1998, p. 1294-1306.
-
Kedadouche M., Thomas M., Tahan A. Empirical mode decomposition of acoustic emission for early detection of bearing defects. Proceedings of the 3rd International Conference on Condition Monitoring of Machinery in Non-Stationary Operations (CMMNO), 2013, p. 367-377.
-
Qin Y. Multicomponent AM-FM demodulation based on energy separation and adaptive filtering. Mechanical Systems and Signal Processing, Vol. 38, Issue 2, 2013, p. 440-459.
-
Wu Z., Huang N. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Advances in Adaptive Data Analysis, Vol. 1, Issue 1, 2009, p. 1-41.
-
Loh C. H., Wu T. C., Huang N. E. Application of the empirical mode decomposition Hilbert spectrum method to identify near-fault ground-motion characteristics and structural responses. Seismological Society of America, Vol. 91, Issue 5, 2001, p. 1339-1357.
-
Meng Z., Gu H. Y., Li S. S. Restraining method for end effect of B-spine empirical mode decomposition based on neural network ensemble. Journal of Mechanical Engineering, Vol. 49, Issue 9, 2013, p. 106-112.
-
Wu Z. H., Huang N. E. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Advances in Adaptive Data Analysis, Vol. 1, Issue 1, 2009, p. 1-41.
-
Lei Y. G., He Z. J., Zi Y. Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mechanical Systems and Signal Processing, Vol. 23, Issue 4, 2009, p. 1327-1338.
-
Bin G. F., Gao J. J., Li X. J., Dhillon B. S. Early fault diagnosis of rotating machinery based on wavelet packets – empirical mode decomposition feature extraction and neural network. Mechanical Systems and Signal Processing, Vol. 27, 2012, p. 696-711.
-
Widodo A., Yang B. S., Han T. Combination of independent component analysis and support vector machines for intelligent faults diagnosis of induction motors. Expert Systems with Applications, Vol. 32, Issue 2, 2007, p. 299-312.
-
Zvokelj M., Zupan S., Prebi I. Multivariate and multiscale monitoring of large-size low-speed bearings using ensemble empirical mode decomposition method combined with principal component analysis. Mechanical Systems and Signal Processing, Vol. 24, Issue 4, 2010, p. 1049-1067.
-
Han M. H., Pan J. L. A fault diagnosis method combined with LMD, sample entropy and energy ratio for roller bearings. Measurement, Vol. 76, 2015, p. 7-19.
-
Du Y. P., Zhang W. J., Zhang Y., Gao Z. Q., Wang X. H. Fault diagnosis of rotating machines for rail vehicles based on local mean decomposition-energy moment-directed acyclic graph support vector machine. Advances in Mechanical Engineering, Vol. 8, Issue 1, 2016, p. 1-6.
-
Liua B., Riemenschneider S., Xu Y. Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum. Mechanical Systems and Signal Processing, Vol. 20, Issue 3, 2006, p. 718-734.
-
Gilles J. Empirical wavelet transform. IEEE Transactions on Signal Processing, Vol. 61, Issue 16, 2013, p. 3999-4010.
-
Xu T. L., Zhang X. Y., Jia Q. X., Lang X. Z. Rolling bearing fault research on wavelet threshold de-noising. Journal of Ship Mechanics, Vol. 16, Issue 10, 2012, p. 1199-1203.
-
Shuai J. N. Research on Acoustic Emission Signals for the Damage of the Fan Blade Based on De-Noising Technology and Blind Source. Nanjing University of Aeronautics and Astronautics, No. 1028701 14-S114, 2013.
-
Kedadouche M., Liu Z. H., Vu V. H. A new approach based on OMA-empirical wavelet transforms for bearing fault diagnosis. Measurement, Vol. 90, 2016, p. 292-308.
-
Juan P., Sanchez A., Adeli H. A new music-empirical wavelet transform methodology for time-frequency analysis of noisy non-linear and non-stationary signals. Digital Signal Processing, Vol. 45, 2015, p. 55-68.
-
Caoa L. J., Chuab K. S., Chong W. K., Lee H. P., Gu Q. M. A comparison of PCA, KPCA and ICA for dimensionality reduction in support vector machine. Neurocomputing, Vol. 55, 2003, p. 321-336.
-
Vapnik V. N. The Nature of Statistical Learning Theory. Springer, New York, 1995.
-
Daubechies I., Lu J. F., Wu H. T. Synchrosqueezed wavelet transforms: an empirical mode decomposition-like tool. Applied and Computational Harmonic Analysis, Vol. 30, Issue 2, 2011, p. 243-261.
-
Daubechies I. Ten lectures on wavelets. The Journal of the Acoustical Society of America, Vol. 93, Issue 3, 1992, p. 1671.
-
Bernhard S., Alexander S., Klaus-Robert M. Nonlinear component analysis as a kernel eigenvalue problem. Neural Computation, Vol. 10, Issue 5, 1998, p. 1299-1319.
-
Li G. Z. Discussion on Selecting the Number of Principal Components. Lanzhou University of Finance and Economics, No. 10741, 2015.
-
Holland J. H. Adaptation in Natural and Artificial Systems: an Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. MIT Press, Cambridge, 1992.
-
Yang C. G. Development of Condition Monitoring System of Motorized Spindle Based on LabVIEW. Jilin University, No. TG659, 2015.
-
Bearing Data Center Seeded Fault Test Data [EB/OL]. The Case Western Reserve University Bearing Data Center Website, 2007, http://csegroups.case.edu/bearingdatacenter/ pages/download-data-file.
-
Hou M. M. Determination of Trace Moisture in Oil by the Measurement of Near Infrared Spectroscopy. Chongqing Technology and Business University, 2012.
About this article
This work is supported by the Project of Jilin Province, Science and Technology Development Plan of the Fault Diagnosis and Condition Monitoring for Motorized Spindle of Machining Center (Grant No. 20160101278JC) and the Subject of the Research and Application of Rapid Test Technology for Reliability of CNC (Grant No. 2016ZX04004-004) and the Project of the Graduate Innovation Fund of Jilin University (Grant No. 2016027).
Fei Chen conceived the idea of using modified empirical wavelet transform to analyze vibration data. Chao Chen applied kernel principal component analysis into reducing dimension and guide the writing of the whole paper. Yifeng Ye conducted the method to better diagnosis the single and compound fault of the motorized spindle and wrote the majority of the paper. Weizheng Chen Carried out the experiments. Binbin Xu processed the experimental data and analyzed the results. Zhaojun Yang edited the manuscript and checked the grammatical and spelling errors.
