Abstract
Condition monitoring of rotating machines has become a more important strategy in structural health monitoring (SHM) research. For fault recognition, the analysis is categorized in two essential main parts: Feature extraction and classification; the first one is used for extracting the information from the signal and the other for decision-making based on these features. A higher accuracy is needed for sensitive places to avoid all kinds of damages that can lead to economic losses and it may affect the human safety as well. In this paper, we propose a new hybrid and automatic approach for bearing faults diagnosis. This method uses a combination between Empirical wavelet Transform (EWT) and Fuzzy logic System (FLS), in order to detect and localize the early degradation of bearing state under different working conditions. EWT build a wavelet filter bank to extract amplitude modulated-frequency modulated component of signal. Modes presenting a high impulsiveness is then selected using the kurtosis indicator. Thereafter, time domain features (TDFs) are applied for the reconstructed signal to extract the fault features which are finally used as an inputs of FLS in order to identify and classify the bearing states. The experimental results shows that the proposed method can accurately extract and classify the bearing fault under variable conditions. Moreover, performance of EWT and empirical mode decomposition (EMD) are studied and shows the superiority of the proposed method.
Highlights
- We proposed a new method of bearing fault diagnosis based on feature extraction and classification.
- EWT is an efficient decomposition method, it constructs a bank of adaptive filters on the acquired vibration signal.
- The original signal is reconstructed based on the decomposed modes which have more impulsivity of shock in them.
- Time domain features are introduced to extract the fault feature vector on the vibration signal.
- A samples part of the characteristic vector is used to learn the fuzzy system, while the rest of the samples are used for testing the approach.
- The proposed approach gives a satisfactory result with a higher efficiency rate.
1. Introduction
Rotating machines are very useful; they cover a large part in the industry and they are introduced in all mechanical equipment; so their diagnostic and maintenance strategies have an important role for factory economics and also for human safety, by avoiding unexpected accidents that can occur due to the presence and non-detection of defects in machines. Large industrial plants and areas which are sensitive to human safety require high precision, because even the slightest mistake can cause unwanted damages [1, 2]. Most researchers use vibration signals, for their simplicity since it requires just the placement of sensors for signal acquisition; without any complex intervention which is the ideal way to detect failure in any rotating machines caused by their cinematic faults. Machine vibration signatures can be used as an early warning to the operator to make a crucial decision before any serious problem or unwanted downtime. The amplitude of the vibration signature gives an indication of the severity of the problem, while the frequency can indicate the source of the fault [3]. For faults diagnosis, researchers have applied various techniques based on vibration analysis [4, 5] such as: Kurtogram, Cepstrum analysis, power spectrum, which can detect the nature of faults in the rotating machines. These techniques are introduced in frequency domain and all spectral techniques are based on FFT. However, to analyze and process signals in time domain, researchers focused on feature-based methods; the procedure strategy can be divided into two main parts: Feature extraction and classification to make a decision which is based on these features. So, various features time domain features (TDFs) are used such as: root mean square (RMS), standard deviation (SD), kurtosis (KU), variance (VAR), entropy (ENT) and etc. The features extraction actually describes the condition of the machine, they have an important role in classifying defects by introducing a set of statistical features as entries to the classification system for faults self-recognition [6].
Mechanical faults generate non-stationary signal emerged with back ground of noise in case of an experimental signal acquisition, where the analysis of conventional methods like FFT technique are complex, so the main problem with the Fourier transform is its lack of information in temporal domain. This simply means that if you are able to fault any frequency that appears in the signal, you are unable to determine when it occurs. For more information, researchers applied other techniques such as time- frequency analysis which can solve this problem and can detect the abnormality due to the presence of faults. So many methods have been applied for faults diagnosis such as Short Time Fourier Transform (STFT), Wavelet Transform (WT), [7-9], Wavelet Packet Transform (WPT), Wigner Ville Distribution (WVD) [10], Empirical Mode Decomposition (EMD) [11-13], Empirical Wavelet Transform (EWT) [14] etc.
One of the most successful methods in machine faults diagnosis in time-frequency domain is wavelet transform (WT) for its distinct advantages [15]. It was used as a de-noising technique for noisy working environment signal processing [16]. However, the high frequency band is not split where the modulation information of machine fault exists. This problem can be overcome by using a wavelet packet transform (WPT) which decomposes the signal in different levels due to their band-pass filters to extract the critical components. These decomposed signals are widely used for features extraction for machine faults diagnosis [17]. For lack of adaptability, WPT is sometimes unable to provide effective information about faults [18, 19]. EMD technique is an adaptive method that decompose a signal into a sum of Intrinsic Mode Function (IMF). However, EMD suffers from the mode mixing, distorted components and the end effects phenomena [20, 21]. By combining the adaptability of EMD and the advantages of WT, Gilles [22], has developed the EWT. Most of researchers introduce the EWT on diagnostic due to their efficiency and accuracy. It has been proved that is better than EMD method for rolling element bearing diagnosis [23, 24].
For automatic fault diagnosis, a classifier is employed to make a quick and reliable decision on the running condition of machinery. The recent works are introduced to give more accuracy to problems; when similar and confusing faults occur in complex systems, leading to difficult identification and localization of the faults. For that raison, a variety of artificial and intelligent techniques have been applied to classify various states. Once the input feature vectors are identified, the decision-making rules could be constructed. This could be done through the use of classification tools based on Artificial Intelligence such as: Artificial Neural Network (ANN) [25], Support Vector Machine (SVM) [26, 27] and Fuzzy Logic System (FLS) [28]. The major problem in pattern recognition based on neurons; for example ANN has a system learning like a black box. The exact number of layers is hard to define in order to achieve the best convergence of output. But in opposition, FLS provides a simple way to achieve a definite output (desired) based on vague and ambiguous information using rules for learning system [29].
In this paper, EWT is proposed to decompose the original signal into different modes, after that we calculate kurtosis values of each decomposed modes. As the kurtosis sensitive to impulsiveness of data in one hand and as the bearing fault generates periodic shocks which increases the kurtosis value of signal in the other, only modes having kurtosis value superior than 3 is kept. Thereafter, statistical features (standard deviation (SD) and the Upper-bound (UPP)) are applied for the reconstructed signal to extract the information on machine condition. Finally, the obtained feature vectors are considered as inputs data of FLS to classify the various bearing condition states, where the classification is based on theory of fuzzy sets. The system output gave information of various faults types for specific size (0.007 inch) and different operating modes (0 to 3 horse-power). The accuracy of this approach is expressed by analyzing signals of bearing with the small fault size, precise identification and localization of the bearing faults under complex and variable working environment.
This paper is organized as follows; Section 1: Introduction, Section 4: EWT, FLS, Statistical features, experimental study and experiment results, Section 5: Conclusion.
2. Empirical wavelet transform
Combining the adaptability of EMD decomposition and the advantages of WT, Gilles [22] has constructed a wavelet filter bank adaptive to extract relevant frequencies of processed signal. In recent works most of researchers use this method for their performance and their reliability in signal processing and also is used for de-noising signal, the Amplitude Modulated-Frequency Modulated (AM-FM) components called modes which are the band-pass supports of decomposition signal. filter model mathematic of these modes is [22]:
where is complex decomposed signal, is frequency-modulated amplitude-modulated signal.
These filters depend on the spectrum of the input signal. First, we note that is the input signal and it’s Fourier spectrum ,we assume that the Fourier support is in segmented in , and we denote that to be the limit between each segments ( for 0: , for : ) , the Fig. 1. Corresponds to the segmentation axis of EWT wavelet construction, and we see the transitional phase around , and we define the complex filters for this support segment [0,]:
Fig. 1Fourier axis segmentation and EWT wavelets construction
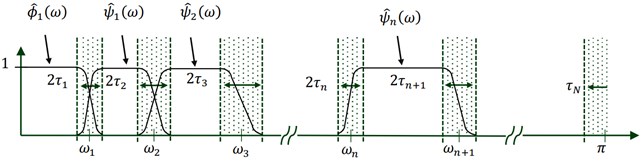
The empirical wavelets are defined from these equations:
Note that the most used function that satisfies this property:
The detail coefficients are obtained by the inner products of the input signal with the empirical wavelets:
The approximation coefficients with scaling function is given:
Finally, the original signal is decomposed into various empirical modes , which is given by:
The signal can be reconstructed as follows:
2.1. Fuzzy logic system
Instead of classic logic (Boolean logic) [30, 31], Lotfi Zadeh created a more precise method resting on the intermediary values between {0, 1}, this method is called Fuzzy Logic where this system is based on functions Membership and their rules. Mamdani and Assilian inspired of Mohamed Zadeh this logic [32], by proposing a more widely used model called Mamdani. Fig. 2 shows the structure of FLS and it can be summarized in three stages, executed in the order.
Fig. 2Fuzzy system structure
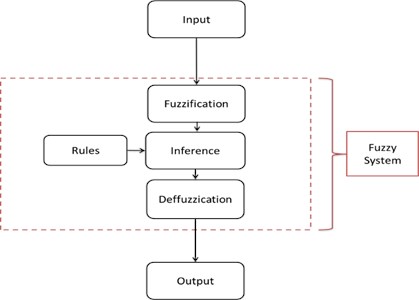
1) Fuzzification: is the first step of fuzzy inference process. It is a domain transformation of crisp into fuzzy inputs to determine the truth’s degree for each rule premise.
2) Inference: is the second step in FIS where, for the premise, we calculated the truth value of each rule and applied it to the conclusion part of each rule. As a result, a blurred subset must be assigned to each output variable for each rule. Usually, the most useful inference rules method are minimum and product. In the case of a minimum, the output adhesion function is cut to a height corresponding to the calculated degree of truth of the rule. When selecting the product, the output adhesion function is scaled according to the calculated degree of truth of the rule.in this step a single fuzzy set is obtained for each output variable.
3) Defuzzification: the process of production results considering the fuzzy sets and degrees of membership, this step covert the crisp value which is obtained on fuzzy output to crisp values where it is performed with one of many defuzzification methods.
Instead of Neural Network learning, the use of rule has an essential part in Fuzzy Inference System which are introduced as follows:
Rule: if is and is than is ;
While: is , is : are the premise of our rule
is : Consequence rule;
And: Operator.
2.2. Basic elements of fuzzy logic (linguistic variables)
The essential notion of linguistic variable was introduced by Zadeh, it immediately suggests that the values of this variable are not numerical, but rather symbolic, in terms of words or expressions of natural language. A linguistic variable is characterized by a triplet (, , ) where: : the variable name; : variable term set, it is the set of names of the linguistic values of of which each value is a fuzzy subset defined in which is the universe of discourse.
2.3. Fuzzy sets and membership functions
Classical logic has two acceptable values 0 or 1, fuzzy logic intervenes to define intermediary of these two values based on the membership sets. Function of membership are defined as follows:
There are different forms of membership functions; trapezoidal and triangular are the most used ones:
2.4. Operators of fuzzy logic
2.5. Operator AND
The fuzzy AND operator is defined as the intersection of two fuzzy sets A and B:
2.6. Operator OR:
The fuzzy OR operator is defined as the union of two fuzzy sets A and B, respectively being the largest fuzzy set contained in A and B:
2.7. Gravity center defuzzification
The center of gravity (GC) method is based on the calculation of the abscissa gravity center of resulting surface (Eq. (14)) obtained on the fuzzy subset of the solution determined by the aggregation of fuzzy rules. Fig. 3. shows the procedure solution of fuzzy logic system using single input and the solution which is given by the method of the center of gravity:
Fig. 3Fuzzy system structure
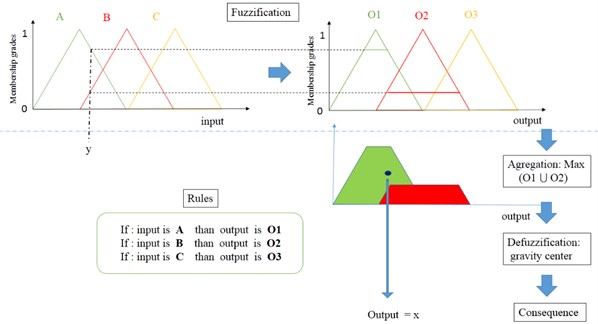
3. Statistical features
These statistical features are calculated to extract information of signal from various states of bearing, were these features are explained as follow [33]:
4. Experimental study
4.1. Experimental description
The signals vibration data are provided by Case Western Reserve University Bearing Data Center [34], the Fig. 4. shows the test rig of bearing in induction motor of 1.5 kw in the left, a dynamometer (in the right), a torque transducer/Encoder (center), the faults diameter is (7, 14, 21, 28) mils, (1 mil = 0.001 inch) the tested bearing is of type (6205-2RS JEM SKF) as it is presented in Fig. 4, knowing that we have two bearing in the motor Fan-End (FE) and the Drive-end (DE).
Fig. 4Test band

Single point defects outer race (ORF), Inner-race (IRF), ball (BF) was introduced separately to the test of bearing using electro-discharge machining (EDM) with different sizes. The vibration data was recorded for motor Horse power (1 HP = 1772 RPM) and for sampling frequency of 12 kHz. We know that the bearing faults produce a repetitive mechanical shockwaves over time, which will create instantaneous frequencies specific to each fault of these defects as shown in Table 1.
Table 1Formula of expected bearing faults frequencies
Type of defect | Formula fault |
Inner-race fault frequency | |
Outer-race fault frequency | |
Rolling-element fault frequency | |
Cage fault frequency |
4.2. Proposed study of rolling bearing
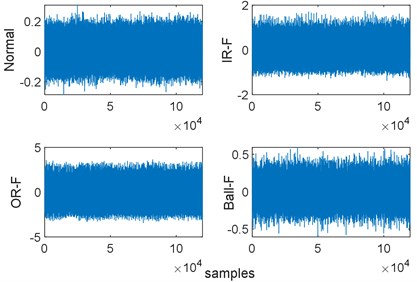
The vibration signals presented in Fig. 5 are processed in order to classify the various bearing faults of 0.007 inch diameter, by using the procedure of mentioned flowchart (Fig. 6), the steps are described as follows:
1) Have an interesting database on the real signals of these two states (healthy and defective) in order to enrich the input data. The Empirical Wavelet Transform is used to decompose the original signal into several band-pass frequencies (modes).
Fig. 5Vibration signals of various bearing fault
2) After decomposition, the signal is reconstructed from the significant modes by calculating the kurtosis value, this indicator has a direct relation with fault impulsivity because it causes repetitive shocks during signal acquisition and it increases the amplitude of vibration signature where the fault characteristic frequency depends on the fault-localisation in bearing.
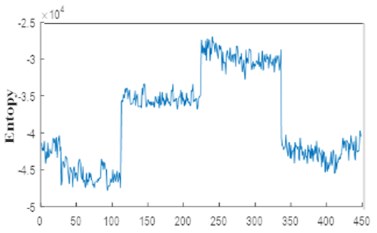
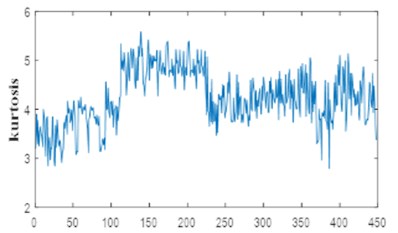
3) Features extraction and selection: the statistical features or time domain features (TDFs) are applied for the reconstructed signal to extract the health condition of bearing. After that, the selected features from their high performance of separability and stability are used as inputs; to avoid all kind of confusion and similiarity of fault states under various working conditions (0 to 3 HP). The Fig. 8. shows variation of feature samples from different states.
4) Features classification: The selected Features will be defined as the input vectors of fuzzy classifier (FLS) to classify the various faults of bearing under different working conditions.
Fig. 6Flowchart of proposed method
Table 2Description of bearing data set
Fault type | Data size vector | Diameter defect | Condition working |
Healthy (H) | 112 | // | [0, 1, 2, 3] hp |
Inner race (IR) | 112 | 0.007 inch | [0, 1, 2, 3] hp |
Outer race (OR) | 112 | 0.007 inch | [0, 1, 2, 3] hp |
Ball (B) | 112 | 0.007 inch | [0, 1, 2, 3] hp |
The corresponding modes shown in Fig. 7. contain the relevant information on bearing condition, we calculate time domain features (TDFs) on the reconstructed signal, knowing that the two indicators of standard deviation (SD) and upper-bound (UPP) have been selected according to the separability of states and especially there is no interesting confusion between them and also the corresponding features values have a great stability; this avoids any kind of confusion states.
Fig. 7Decomposed signal using EWT
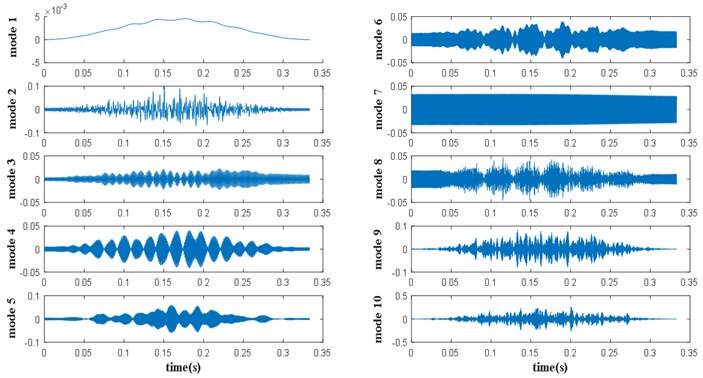
Fig. 8Feature extraction of 0.007 inch of various defects
a)
b)
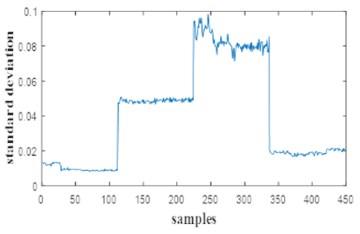
c)
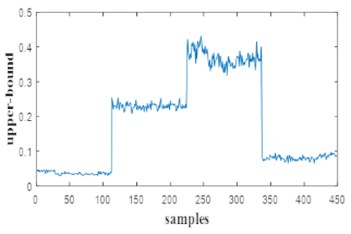
d)
For this study, a part of initial vector 35.71 % was used for learning system and the rest for testing. The minimum and the maximum has been extracted from the selected features as the Fig. 9 and Fig. 10. show, the interval min-max of features states are the inputs of FLS. The membership of input and output are shown in Fig. 11, Fig. 12 respectively.
When the fuzzification part is completed, the laws must be made for the defuzzification where this part is essential for classification. The result of the fuzzy output depends on the laws implemented rules for fuzzy learning system.
Rules are used for training fuzzy system that is based on the fuzzified memberships of inputs, the (SD, UPP) features have been introduced as two inputs for classifier to enhance and confirm the fuzzified entries (operator and) and eliminating the undefined values from a signal (operator OR) using the following rules:
• If: SD is H and UPP is H the output is H,
• If: SD is IR and UPP is IR the output is IR,
• If: SD is OR and UPP is OR the output is OR,
• If: SD is B and UPP is B the output is B,
• If: SD is H or UPP is H the output is H,
• If: SD is IR or UPP is IR the output is IR,
• If: SD is OR or UPP is OR the output is OR,
• If: SD is B or UPP is B the output is B.
Fig. 9Minima and maxima of standard deviation feature
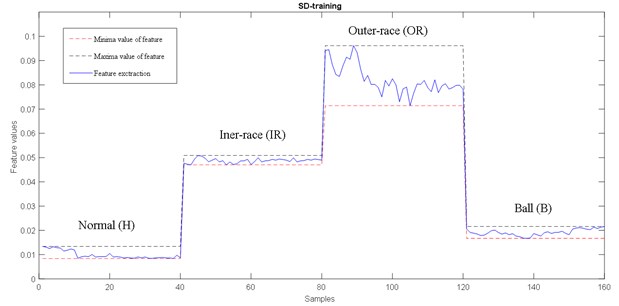
Fig. 10Minima and maxima of upper-bound feature
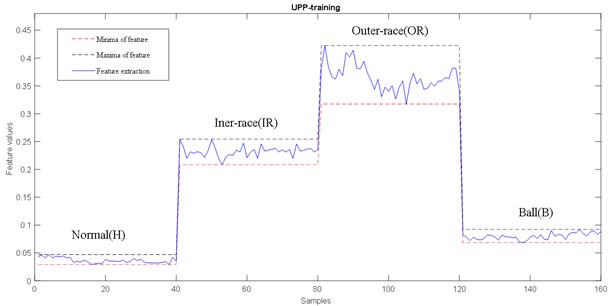
For testing this approach, 64.29 % of the input vector is introduced for the FLS classifier, in order to show the effectiveness of this method, we will test the fuzzy system with new samples which are not introduced in the learning system. The output correspond to forth classes of bearing states under variable working condition. The data contains various faults (IR ,OR,B) of 0.007 inch under different working conditions (0 to 3 HP) as it is represented in Table 4, where classification result is given in the Fig. 13.
Fig. 13 shows the classification of the proposed approach; all samples are classified with some fluctuations that are very closer to the desired values. Based on this result, we conclude that this classification result gives a good performance and satisfactory detection and identification for bearing fault.
To confirm the proposed diagnosis strategy, we will compare the given approach with other decomposition method using the same classifier, inputs and rules. First, we give the classification without EWT decomposition using SD-UPP (standard deviation-upperbound) features as inputs, the result is presented in the Fig. 14. From the last figure, we can see a correct classification of H samples and acceptable classification in B samples with some fluctuation in OR-IR samples.
Table 3Gravity center of output
Bearing states | Healthy | IR-fault | OR-fault | Ball-fault |
Working condition (HP) | 0 1 2 3 | 0 1 2 3 | 0 1 2 3 | 0 1 2 3 |
Length of training data | 40 | 40 | 40 | 40 |
Desired output | Gravity center of H | Gravity center of IR | Gravity center of OR | Gravity center of B |
Value of desired classes | 0.09808 | 0.3333 | 0.6642 | 0.9019 |
Fig. 11Membership functions of inputs fuzzy logic
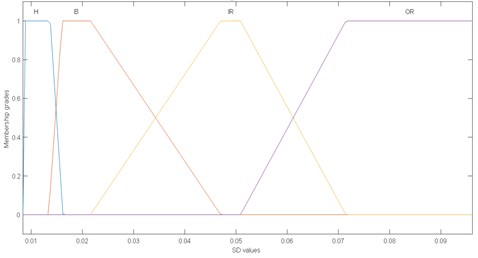
a) First input fuzzification
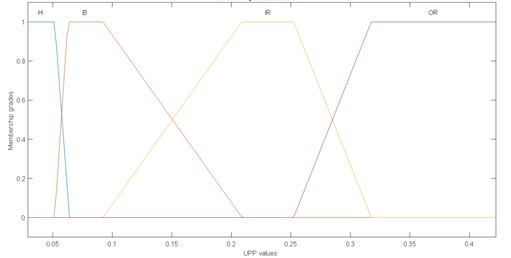
b) Second input fuzzification
Fig. 12Membership functions of output fuzzy logic
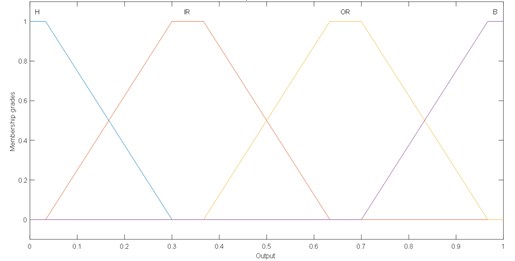
Fig. 15 presents a classification of SD-UPP features using EMD decomposition. We observed a large fluctuation of H state in 1797 rpm (HP0) which can lead to unsatisfactory classification. Generally, excepting Healthy samples, the classification is good and acceptable.
On the basis of compared results, the proposed approach gives a satisfactory classification to early fault detection and identification of rolling bearing under various working condition.
Fig. 13Classification result of proposed method
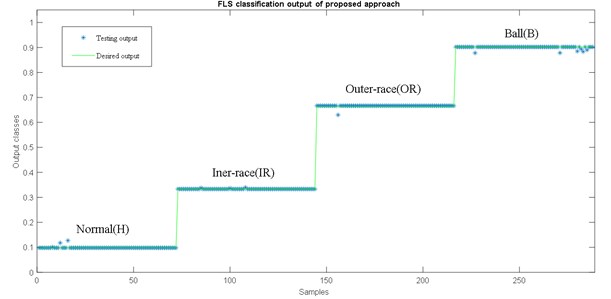
Fig. 14Classification result of proposed method without EWT
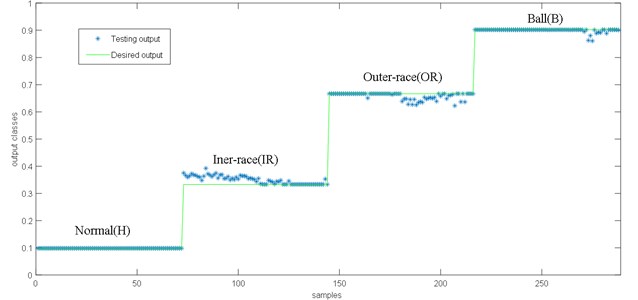
Fig. 15Classification result of proposed method with EMD
5. Conclusions
Early detection of bearing faults is one of important research fields. It permits to reduce maintenance cost and avoiding economic losses and human risks. To monitor the condition of bearing for various condition modes and different fault types in noisy environment, which that constitutes a new challenge on rolling bearing diagnosis. For the complexity process and the reason of effectiveness, a significant research has been applied to health monitoring with emergence a variety of methods and techniques in signal processing. In this paper we present a Fuzzy Logic System decision using EWT and TDFs. The procedure is based on feature extraction and classification for obtaining the current health of rotating component. First, the vibration signal is decomposed into many modes to reconstruct new vibration signal. After that, SD-UPP features are applied for the reconstructed signal and the obtained feature vectors will be defined as inputs of FLS; for an automatic and intelligent fault detection and identification. This proposed method was applied on real experimental data where the results show the effectiveness of the approach for bearing fault diagnosis under various working condition.
References
-
Miao, Wang Q., Pecht D. A probabilistic description scheme for rotating machinery health evaluation. Journal of Mechanical Science and Technology, Vol. 24, Issue 12, 2010, p. 2421-2430.
-
Yang Z., Chen X., Xie Y., et al. The hybrid multivariate analysis method for damage detection. Structural Control and Health Monitoring, Vol. 23, Issue 1, 2016, p. 123-143.
-
Goyal D., Pabla B. S. The vibration monitoring methods and signal processing techniques for structural health monitoring: a review. Archives of Computational Methods in Engineering, Vol. 23, Issue 4, 2016, p. 585-594.
-
Lei Y., He Z., et al. Application of an improved kurtogram method for fault diagnosis of rolling element bearings. Mechanical Systems and Signal Processing, Vol. 25, Issue 5, 2011, p. 1738-1749.
-
Wang D., Guo W., Wang X. A joint sparse wavelet coefficient extraction and adaptive noise reduction method in recovery of weak bearing fault features from multicomponent signal mixture. Applied Soft Computin, Vol. 13, Issue 10, 2013, p. 4097-4104.
-
Ali Jaouher Ben, Fnaiech Nader, Saidi Lotfi, et al. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Applied Acoustics, Vol. 89, 2015, p. 16-27.
-
Yan R., Gao R., Chen X. Wavelets for fault diagnosis of rotary machines: a review with applications. Signal Processing, Vol. 96, 2014, p. 1-15.
-
Mallat S. A Wavelet Tour of Signal Processing. 3d Edition, The Sparse Way, 2009, p. 832.
-
Combastel C., Lesecq S., Petropol S., Gentil S. Model-based and wavelet approaches to induction motor on-line fault detection. Control Engineering Practice, Vol. 10, Issue 5, 2002, p. 493-509.
-
Blodt M., Bonacci D., Regnier J., Chabert M. On-line monitoring of mechanical faults in variable-speed induction motor drives using Wigner distribution. IEEE Transactions on Industrial Electronics, Vol. 55, Issue 2, 2008, p. 522-533.
-
Lei Y., Lin J., He Z., et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mechanical Systems and Signal Processing, Vol. 35, Issues 1-2, 2013, p. 108-126.
-
Gao Q., Duan C., Fan H. Rotating machine fault diagnosis using empirical mode decomposition. Mechanical Systems and Signal Processing, Vol. 22, Issue 5, 2008, p. 1072-1081.
-
Li Y., Xu M., Wei Y., et al. An improvement EMD method based on the optimized rational Hermite interpolation approach and its application to gear fault diagnosis. Measurement, Vol. 63, Issue 2, 2015, p. 330-345.
-
Merainani B., Benazzouz D., Rahmoune C. Early detection of tooth crack damage in gearbox using empirical wavelet transform combined by Hilbert transform. Journal of Vibration and Control, Vol. 23, Issue 10, 2017, p. 1623-1634.
-
Kankar P., Sharma S., And Harsha S. Fault diagnosis of ball bearings using continuous wavelet transform. Applied Soft Computing, Vol. 11, Issue 2, 2011, p. 2300-2312.
-
Kulkarni G., Sahasrabudhe D. Application of wavelet transform for fault diagnosis of rolling element bearings. International Journal of Technology Enhancements and Emerging Engineering Research, Vol. 2, Issue 4, 2013, p. 138-148.
-
Xu Q., Lia Z. Recognition of wear mode using multi-variable synthesis approach based on wavelet packet and improved three-line method. Mechanical Systems and Signal Processing, Vol. 21, Issue 8, 2007, p. 3146-3166.
-
Chen S. W., Chen Y. H. Hardware design and implementation of a wavelet de-noising procedure for medical signal processing. Sensors, Vol. 15, 2015, p. 26396-26414.
-
Zhong J. H., Wong P. K., Yang Z. X. Simultaneous-fault diagnosis of gearboxes using probabilistic committee machine. Sensors, Vol. 16, Issue 2, 2016, p. 185.
-
Xiao Q., Li J., Bai Z., Sun J., Zhou N., Zeng Z. A small leak detection method based on VMD adaptive de-noising and ambiguity correlation classification intended for natural gas pipelines. Sensors, Vol. 16, Issue 12, 2009, p. 2116.
-
Wang T., Zhang M., Yu Q., Zhang H. Comparing the applications of EMD and EEMD on time-frequency analysis of seismic signal. Journal of Applied Geophysics, Vol. 83, 2012, p. 29-34.
-
Gilles J. Empirical wavelet transform. IEEE Transactions on Signal Processing, Vol. 61, Issue 16, 2013, p. 3999-401.
-
Maheshwari S., Pachori R. B., Acharya U. R. Automated diagnosis of glaucoma using empirical wavelet transform and correntropy features extracted from fundus images. EEE Journal of Biomedical and Health Informatics, Vol. 21, Issue 3, 2016, p. 803-813.
-
Jiang Y., Zhu H., Li Z. A new compound faults detection method for rolling bearings based on empirical wavelet transform and chaotic oscillator. Chaos Soliton Fractals, Vol. 89, 2016, p. 8-19.
-
Wang C., Yuan K., Shen P., et al. Applications of fault diagnosis in rotating machinery by using time series analysis with neural network. Expert Systems with Applications, Vol. 37, Issue 2, 2010, p. 1696-1702.
-
Fernández-Francos D., Martinez D., Fontenla-Romero O., et al. Automatic bearing fault diagnosis based on one-class v-SVM. Computers and Industrial Engineering, Vol. 64, Issue 1, 2013, p. 357-365.
-
Wyk B., Wyk M., Qi G. Difference histograms: a new tool for time series analysis applied to bearing fault diagnosis. Pattern Recognition Letters, Vol. 30, 2013, p. 595-599.
-
Bezdek J. C. Pattern Recognition with Fuzzy Objective Function Algorithms. Springer, 2008.
-
Krishnakumari A., Elayaperumal A., Saravanan M., Arvindan C. Fault diagnostics of spur gear using decision tree and fuzzy classifier. The International Journal of Advanced Manufacturing Technology, Vol. 89, Issues 9-12, 2017, p. 3487-3494.
-
Hemba S., Islam N. Fuzzy logic: a review. International Journal of Computer Sciences and Engineering, Vol. 5, Issue 2, 2017, p. 61-63.
-
Kasbe T., Pippal R. S. Dengue fever: state-of-the-art symptoms and diagnosis. International Journal of Computer Sciences and Engineering, Vol. 4, Issue 6, 2016, p. 26-30.
-
Dadios E. P. Fuzzy Logic Controls, Concepts, Theories and Applications. IntechOpen, 2012, p. 325-350.
-
Javed Kamran, Gouriveau Rafael, Zerhouni Noureddine, Nectoux Patrick A feature extraction procedure based on trigonometric functions and cumulative descriptors to enhance prognostics modeling. IEEE International Conference on Prognostics and Health Management, United States, 2013.
-
Case Western Reserve University Bearing Data Center, http://csegroups.case.edu/bearingdatacenter/home.
