Abstract
For RV reducer widely used in Robots, this work develops a lumped parameter model to investigate free vibration properties of general description. The dynamic model admits three planar degrees of freedom for each component and includes key factors affecting vibration such as involute and cycloid gear mesh stiffness, crankshaft bending stiffness and bearing stiffness. For the linear case, examine of the associated eigenvalue problem reveals the specific structure of vibration modes. The modes are classified into three types: rotational, translational, and planetary component modes. All vibration modes fall into one of these three categories. The unique properties of each type is examined which is analytically verified with candidate mode method. Furthermore, the work investigates effects of parameters, which include stiffness, mass, moment of inertia and crankshaft eccentricity, on natural frequencies of three vibration modes and crankshaft eccentricity is in particular scrutinized. It is helpful for understanding the relationship between parameters and vibration modes.
1. Introduction
Rotate Vector (RV) reducer is a kind of newly developed reducer on the base of traditional cycloid gears, which has many advantages, such as large transmission ratio, multi-mesh and high carrying capacity, high transmission efficiency and stable working performance. RV reducer is widely used in many applications due to these advantages. However, noise generated by RV reducer and vibration transmitted to the surrounding structure are concerns among designers.
RV reducer is a special planetary gear which joins involute gears and cycloid gears together. The vibration of planetary gears has been extensively studied. For single-stage planetary gear, Cunliffe et al. [1] explored the characteristics of vibration modes in a thirteen degree of freedom planetary gear and identified the conclusions by performing accompanying experiments. Botman [2] investigated the modes of an eighteen degree of freedom system and the effects of planet pin stiffness on the natural frequencies. Natural frequencies of planetary gears with unequal planet stiffness were studied in [3]. Kahraman [4] proposed a simplified rotational lumped parameter model which does not include component translation. It was used to predict natural frequencies and vibration modes. Kahraman [5] also introduced a more complex model that includes all six rigid body degrees of freedom of each gear component to analyze the full three-dimensional motion expected in a helical system. Lin et al. [6] improved purely rotational model by including translational degrees. Using the transverse-torsional model, they analyzed the free vibration and proved that they possess highly structured modal properties. There are exactly three types of modes: rotational, translational and planet mode. They show certain unique properties for these modes because of cyclic symmetry. Furthermore, Lin et al. [7] analyzed vibration characteristics of planetary gears with unequally spaced planets. Wu et al. [8, 9] removed the assumption of a rigid ring gear, considering its elastic deformation and the subsequent effects on the modal properties. Zhu et al. [10] considered flexibility of pin and studied its effect on the dynamic behaviors of wind turbine planetary gear drives. Bahk et al. [11] used the transverse-torsional model and computational methods to investigate nonlinear behavior in an equally spaced spur planetary gear. Parker et al. [12] performed computational modal tests that simulated experimental impact testing and the finite element results are consistent with results from the analytical model. Qian et al. [13] analyzed the natural frequencies and vibration modes of a planetary gear system with results of a finite element model. Ericson et al. [14] correlated the analytical and computational models with modal vibration experiments. Three types of vibration modes were confirmed experimentally. All research above is for simple, single stage planetary gear.
For compound or multi-stage planetary gear, a large amount of research has also been performed, too. Kahraman [15] conducted the analytical study of the vibration of compound planetary gears with a purely rotational model. He derived equations of motion for each configuration and summarized the vibration properties from numerical results. However, the results apply only to the specific configurations in the paper. Guo et al. [16] developed a purely rotational model that is suitable for compound planetary gears with general configurations, to demonstrate the natural frequency and vibration mode properties, and to analytically prove these structured vibration properties. Kiracofe et al. [17] and Dhouib et al. [18] extended previous lateral-torsional model to compound, multi-stage planetary gears, and proved that they exhibited modal characteristics similar to simple, single-stage planetary gears. Vibration property of planetary gears with gyroscopic effects was investigated in [19, 20].
Compared with common planetary gears, free vibration properties of RV reducer have received little research attention. Lai [21] presents a mathematical model and procedures to design the epicycloid planet gear of cycloid drives from perspective of geometry. Blagojević et al. [22] developed a dynamic model of a single-stage cycloid drive and found that the biggest influence on dynamic operating of the cycloid drive comes from the coefficient of the damping during the contact between the cycloid gear tooth and the central gear roller as well as from its stiffness. Fedosovskii et al. [23] studies the effect of a cycloid gear geometry on loading capacity of K-H-V reducers. Zhang et al. [24] developed a 5-DOF dynamic model to calculate natural frequencies and made experiments with RV-6AII to verify the model. Zhang et al. [25-26] established a 25-DOF dynamic model by lumped method. Results show that the support bearings stiffness of planet carrier and the bending stiffness of crankshaft have obvious effect on the nature frequency.
Despite research above, systematic description of RV reducer’s free vibration properties has not been considered. Unlike common planetary gears, RV reducer is not cyclic symmetric due to crankshafts and cycloid wheels’ configuration. So conclusions of common planetary gears with cyclic symmetry structure are not completely applicable to RV reducer. For this reason, it is essential to study the systematic characterization of RV reducer’s free vibration properties. The objective of this paper is to explore the structure of natural frequency and vibration modes of general RV reducers, and investigate effect of stiffness, mass, moment of inertia and crankshaft eccentricity on natural frequencies. To a RV reducer designer, the prediction of natural frequencies allows resonance conditions to be avoided when designing this planetary gear system. The classification of modes into various types and knowledge of the number of numerically different natural frequencies is also important for avoiding resonant response, reducing excitation of particular mode types, and understanding whether response in a particular mode will generate torque (rotational modes), force (translational modes), or neither (planetary modes) to the structures supporting the central gears (sun and ring).
2. Dynamic model and equation
RV reducer is a two stage planetary gear system which is characterized by joining involute gears and cycloid gears together as shown in Fig. 1. The high-speed stage is K-H type differential planetary gear train, which consists of the sun, cyclic symmetry planets and the output wheel. The low-speed stage is K-H-V type epicyclic planetary gear train, which consists of crankshafts, cycloid wheels, needle wheel and the carrier. Unlike cyclic symmetry structure, crankshafts and cycloid wheels are in phase structure because they are arranged in identical bias direction. The carrier and output wheel are fixed by bolts as one component.
RV reducer dynamic model is built using the same strategies as those used for general planetary gears [6]. A lumped-parameter model is shown in Fig. 2. Each of the sun, planets, crankshafts, cycloid wheels and the output wheel is treated as rigid bodies. Component flexibility, bearings and gear meshes are represented by linear springs. The supports of the components are modeled as two perpendicular springs with equal stiffness. Each component has three degrees of freedom: two translations and one rotation. Translational coordinates , , and are assigned to the sun and output wheel. The and coordinates are chosen to be positive towards the equilibrium position of the arbitrarily chosen first planet or crankshaft at time 0. Translational coordinates , , , , and , are assigned to planet , crankshaft and cycloid wheel . All rotational coordinates are chosen to be . This is illustrated in Fig. 2, where , , , and are shown.
Fig. 1Schematic of RV reducer: 1 – sun gear, 2 – planet, 3 – crankshaft, 4 – cycloid wheel, 5 – needle wheel, 6 – carrier, 7 – output wheel
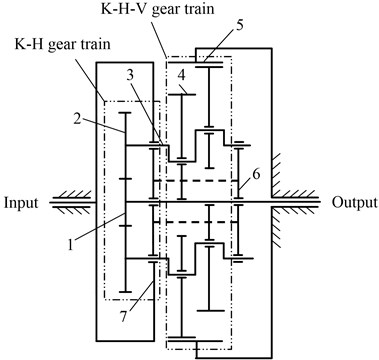
Fig. 2Lumped parameter model of RV reducer and coordinates
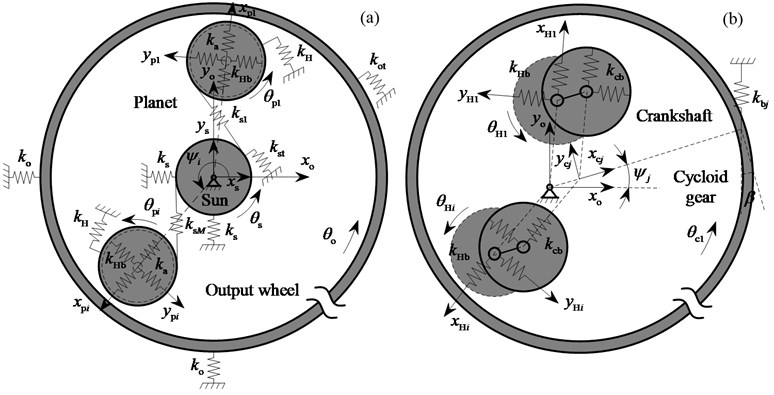
According to the Newton’s second law and theorem of angular momentum, the equations of motion can be derived. Taking the cycloid gear as an example, Fig. 2(b) shows a cycloid-pin mesh with mass , moment of inertia , radius of planet distribution circle center and radius of cycloid gear pitch circle . Notation is the equivalent pressure angle of the cycloid-pin mesh. The cycloid gear suffers support force from crankshafts and mesh force from pins. The equations are:
where the deflections of the cycloid gear support spring and the deflection of the th cycloid-pin mesh spring are:
Notation is crankshaft eccentricity:
means the angle between the coordinates and .
The equations of motion for the sun, planets, crankshafts, and output wheel can be obtained in a similar manner. Assembling the system equations, the governing equations of motion can be written in matrix form as:
where the matrix components are given in the Appendix. is the inertia matrix. is the bearing stiffness matrix. is the meshing stiffness matrix which can be decomposed into mean and time-varying components. is the applied external force and torque.
3. Natural frequencies and vibration modes
To determine the nature frequencies and vibration modes the time-invariant system is considered. All externally applied moments are assumed to be zero. The associated eigenvalue problem is:
where are natural frequencies and the vibration modes have the form with for the sun, for planet , for crankshaft , for cycloid wheel and for the output wheel.
Expanding Eq. (3) into groups of equations associated with the individual components gives:
where the 3×3 submatrices in Eqs. (4)-(8) are given in the Appendix and used in the subsequent analysis.
The assumptions above lead to a combination of cyclic symmetry and in phase structure with distinctive vibration properties. These properties are first illustrated by a numerical example with the parameters shown in Table 1.
Table 1Parameters of an example RV reducer
Items | Sun | Planet | Crankshaft | Cycloid Gear | Carrier |
Mass/kg | 1.30 | 0.88 | 0.40 | 2.76 | 15.33 |
Moment of inertia / kgm2 | 4.44×10-4 | 1.01×10-3 | 7.56×10-5 | 2.09×10-2 | 1.06×10-1 |
Base diameter / mm | 10.57 | 48.63 | 2.20 | 85.80 | 63.50 |
Support stiffness / (N/m) | 4.19×107, 2.33×108, 1.51×109 | ||||
Bearing stiffness / (N/m) | 9.76×108, 9.84×108 | ||||
Mesh stiffness / (N/m) | 2.68×108, 8.35×108 | ||||
Torsional stiffness / (Nm/rad) | 1.16×104, 6.99×104 | ||||
The nature frequencies and their multiplicities are shown in Table 2. All vibration modes for RV reducers can be classified into one of three types which are shown in Fig. 3.
Fig. 3Vibration modes of RV reducer
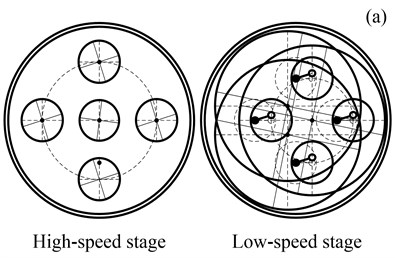
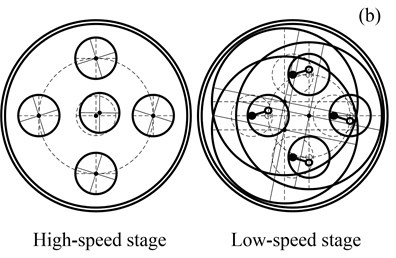
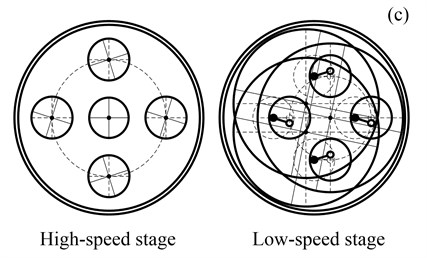
Fig. 3 illustrates three typical vibration modes of RV reducer. Fig. 3(a) shows a type of mode where all central components (the sun and output wheel) have pure rotation and no translation. These are called rotational modes. In a rotational mode, all planet components (planets, crankshafts and the cycloid gears) have identical motion. There are exactly 11 rotational modes, each with an associated natural frequency of multiplicity one.
Fig. 3(b) shows a type of mode where all central components have pure translational motion and no rotation. These are named translational modes. There are exactly 11 degenerate pairs of translational modes, where each pair has an associated natural frequency of multiplicity two.
Fig. 3(c) illustrates a type of mode where the central components have no motion and the planet components deflect. These are named planetary component modes. There are exactly 6 or 3 degenerate pairs of modes, each with an associated natural frequency of multiplicity M-3 or N-3.
In the following sections, the eigensolution properties identified in the example are analytically shown to be true for general RV reducers.
Table 2Natural frequencies (Hz) with multiplicity m for various numbers of planets M and N cycloid wheels
3 | 3 | 3 | 4 | 5 | |
3 | 4 | 5 | 3 | 3 | |
456.56 | 499.63 | 532.20 | 454.13 | 449.47 | |
694.49 | 694.04 | 693.79 | 667.28 | 643.89 | |
2034.15 | 2025.39 | 2015.27 | 2118.41 | 2181.95 | |
2455.49 | 2407.62 | 2349.32 | 2501.34 | 2513.25 | |
2645.83 | 2589.33 | 2574.83 | 2932.20 | 3223.88 | |
4092.77 | 3979.59 | 3883.12 | 4330.62 | 4470.15 | |
5213.45 | 5213.52 | 5213.57 | 5802.57 | 5968.84 | |
5583.11 | 5598.21 | 5607.45 | 6017.18 | 6725.28 | |
6395.64 | 6578.29 | 6748.81 | 6858.17 | 7382.61 | |
16241.42 | 18055.34 | 19703.60 | 16241.42 | 16241.42 | |
16576.88 | 18375.22 | 20008.09 | 16688.60 | 16800.30 | |
776.81 | 791.89 | 805.35 | 750.85 | 729.21 | |
1999.34 | 2054.02 | 2088.99 | 2057.64 | 2098.51 | |
2262.19 | 2302.61 | 2337.30 | 2334.75 | 2372.00 | |
2573.12 | 2579.72 | 2585.18 | 2682.82 | 2818.86 | |
3713.51 | 3682.54 | 3657.23 | 4203.33 | 4565.57 | |
4209.01 | 4128.78 | 4071.80 | 4797.77 | 5304.61 | |
4270.38 | 4189.10 | 4132.08 | 4876.53 | 5404.39 | |
5255.98 | 5370.58 | 5465.94 | 5405.06 | 5599.51 | |
6080.19 | 6126.02 | 6183.41 | 6235.16 | 6402.26 | |
16554.35 | 18354.85 | 19989.19 | 16666.35 | 16782.25 | |
16585.97 | 18378.10 | 20007.22 | 16707.17 | 16831.56 | |
1971.55 | 1971.55 | ||||
2516.17 | 2516.17 | ||||
4808.66 | 4808.66 | ||||
5736.97 | 5736.97 | ||||
16241.37 | 16241.37 | ||||
16241.77 | 16831.10 | ||||
3877.22 | 3877.22 | ||||
5203.98 | 5203.98 | ||||
5280.81 | 5280.81 |
3.1. Rotational modes
A rotational mode has the following characteristics:
(1) The associated natural frequency is distinct;
(2) The translation of the sun and the output wheel are zero;
(3) All planetary components have identical deflections.
Therefore, a candidate rotational mode has the form:
This candidate mode must satisfy the eigenvalue problem of Eqs. (4)-(8). Insertion of into Eq. (4) produces only one equation:
In the same way, insertion of into Eqs. (5)-(8) produces:
Eqs. (10)-(14) consist of eleven linear, homogenous equations for eleven unknowns and the parameter . Thus Eqs. (4)-(8) reduce to an eleven degree of freedom eigenvalue problem. Solution of this reduced eigenvalue problem yields eleven eigensolutions . From the solutions, rotational vibration modes of the full system are constructed according to Eq. (9). These eleven vibration modes have no degeneracy because cyclic rotation of the planet, crankshaft, and cycloid wheel indices in yields the same mode rather than an independent one. Thus, there are exactly eleven distinct rotational modes with the structure of Eq. (9).
3.2. Translational modes
A translational mode has the following characteristics:
(1) The associated natural frequency has multiplicity two, so there is a pair of orthonormal vibration modes corresponding to each natural frequency;
(2) The rotation of the sun and the output wheel are zero. Furthermore, the sun and output wheel translations in the degenerate modes and are related by and or (, ).
(3) There isn’t special rules between the planetary component deflections for a pair of vibration modes and (, , ). But there are six unknown numbers for one type of planetary component.
A pair of candidate translational modes is expressed as:
Analogous to the procedure for rotational modes, and are substituted into Eq. (4). For both and , the third equation of Eq. (16) and Eq. (17) vanishes and the first two equations yield the same equations. Similarly, Eq. (8) provide two constraints on components of and . Insertion of and into Eq. (5-7), there are still eighteen constraint equations. Hence, twenty two independent equations are obtained to constitute an eigenvalue problem. Note that and are interchangeable, so these eigensolutions must consist of eleven pairs of eigenvectors and eleven eigenvalues with multiplicity two.
3.3. Planetary component modes
A planetary component mode has the following characteristics:
(1) The associated natural frequency has multiplicity 3 or 3.
(2) The rotation and translation of the sun and the output wheel are zero.
(3) The planetary component deflections are scalar multiples of the first component’s deflection or deflection which is linearly independent of it.
So a candidate planetary mode associated with planets and crankshafts is expressed as:
A candidate planetary mode associated with cycloid wheels is expressed as:
where and (, , ) are linearly independent, or .
The work illustrates the characteristics of planetary component modes with Eq. (17). Modes associated with planets and crankshafts are similar. Insertion of into Eqs. (4)-(8) yields:
Eq. (18) are under-determined equations with 3 sets of independent solutions for the . The eigensolutions of Eq. (19) are independent of . For each of the eigensolutions obtained from Eq. (19), 3 independent vibration modes can be constructed according to Eq. (17) with the determined from Eq. (31). Therefore, in Eq. (17) is a vibration mode and has degeneracy 3.
Compared with common planetary reducer’s translational and planet modes [6], the form of RV reducer’s translational and planetary component modes is different. It is because of the crankshaft eccentricity which makes crankshafts and cycloid gears in phase structure. When crankshaft eccentricity is zero, the structure of RV reducer changes to cyclic symmetry and the form of the two modes is the same with common planetary reducer. Therefore, eccentricity leads to unique vibration modes of RV reducer.
4. Effect of parameters on natural frequencies
Natural frequencies are typically a major concern. To examine effect of different parameters on natural frequencies of three vibration modes, Eq. (3) is used to obtain natural frequencies. The section studies effect of stiffness, mass, moment of inertia and crankshaft eccentricity.
4.1. Stiffness
To analyze effect of stiffness on natural frequencies, only the studied stiffness parameter is varied, while all other parameters are invariant. The central components stiffness , , and are investigated for RV reducer with three planets, three crankshafts and four cycloid wheels.
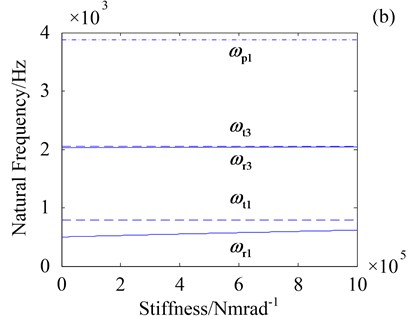
Fig. 4 shows natural frequencies of three vibration modes versus the central components transverse support stiffness and . It shows that natural frequencies of translational mode ( and ) increase as stiffness and increase, respectively. Besides, natural frequencies of rotational mode ( and ) and planetary mode () keep invariable as stiffness and increase, which suggests that natural frequencies of rotational and planetary component modes are independent of the central components transverse support stiffness.
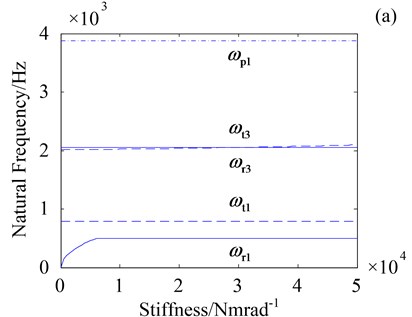
Fig. 5 shows natural frequencies of three vibration modes versus the central components torsional support stiffness and . In Fig. 5, only natural frequencies of rotational mode ( and ) increase as stiffness and increase. Natural frequencies of translational mode ( and ) and planetary component mode () keep invariable as stiffness and increase, which suggests that natural frequencies of translational and planetary component modes are independent of the central components torsional support stiffness. Moreover, Fig.5 implies that low frequency is more sensitive to stiffness and .
Fig. 4Natural frequencies versus ks and ko
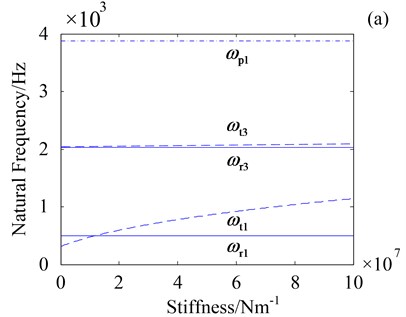
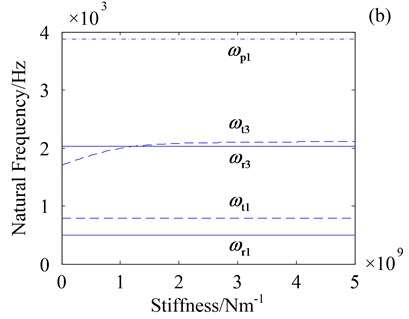
Fig. 5Effect of kst and kot on natural frequencies
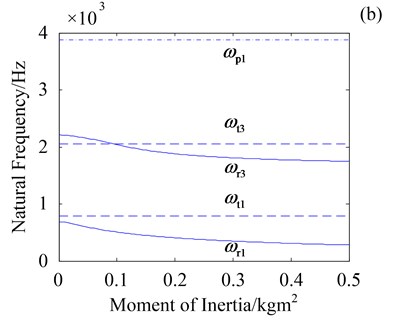
4.2. Mass and moment of inertia
Similar to stiffness, effect of mass and moment of inertia on natural frequencies is also investigated. The central components mass and moment of inertia , , and are studied for RV reducer with three planets, three crankshafts and four cycloid wheels.
Fig. 6 shows natural frequencies of three vibration modes versus the central components mass and . It shows that natural frequencies of translational mode ( and ) decrease as stiffness and increase, respectively. Besides, natural frequencies of rotational mode ( and ) and planetary mode () keep invariable as mass and increase, which suggests that natural frequencies of rotational and planetary component modes are independent of the central components mass.
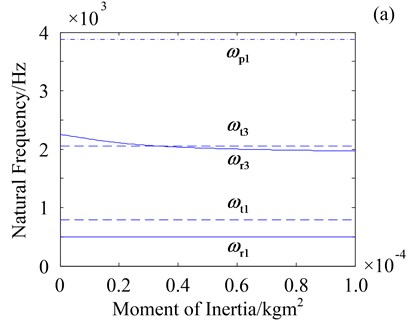
Fig. 7 shows natural frequencies of three vibration modes versus the central components moment of inertia and . In Fig. 5, only natural frequencies of rotational mode ( and ) decrease as moment of inertia and increase. Natural frequencies of translational mode ( and ) and planetary component mode () keep invariable as stiffness and increase, which suggests that natural frequencies of translational and planetary component modes are independent of the central components torsional support stiffness.
Fig. 6Effect of ms and mo on natural frequencies
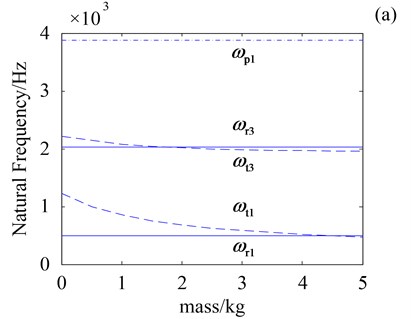
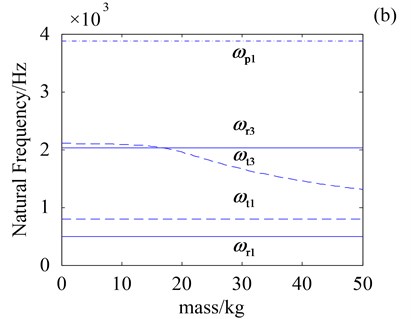
Fig. 7Effect of Js and Jo on natural frequencies
4.3. Crankshaft eccentricity
Effect of crankshaft eccentricity on natural frequencies of three modes is studied. Results in Figs. 8-11 show that eccentricity obviously affects natural frequencies.
Fig. 8 shows effect of variation in crankshaft eccentricity on natural frequencies of three vibration modes for RV reducer with three planets, three crankshafts and four cycloid wheels. Overall, eccentricity has impact on amplitude and variation trend of frequencies in different degree and way. In Fig. 8(a), natural frequency of rotational mode () has little change in amplitude. It first increases and then decreases as eccentricity increases. It suggests that turning point of appears with eccentricity increasing. reaches its maximum when eccentricity is 4.61 mm. Fig. 8(b) shows that eccentricity has larger impact on natural frequency of translational mode (). It increases monotonically as eccentricity increases. In Fig. 8(c), natural frequency of planetary component mode () does not change as eccentricity increases.
Fig. 9 shows effect of variation in crankshaft eccentricity on natural frequencies of three vibration modes for RV reducer with four planets, four crankshafts and three cycloid wheels. Like the case above, eccentricity has similar influence on natural frequencies of rotational and translational modes. However, it has apparent impact on natural frequencies () of planetary component mode which is different from above. It is because that there are four crankshafts which have deflection for planetary component mode. Eccentricity has obvious impact on . first increases and then decreases.
Fig. 8Effect of e on natural frequencies
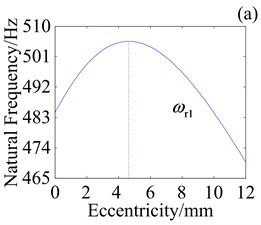
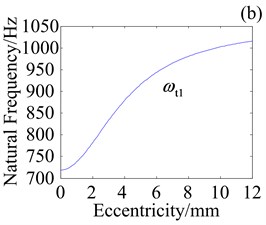
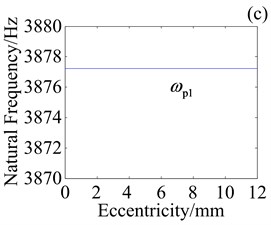
Fig. 9Effect of e on natural frequencies
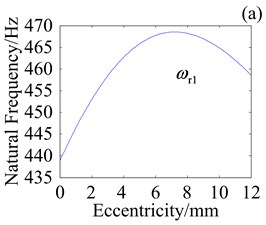
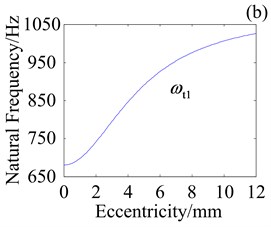
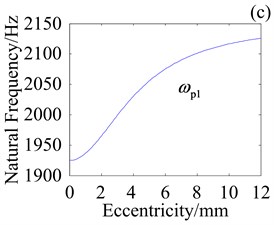
Fig. 10Effect of e on natural frequencies with kcb= 108 N/m
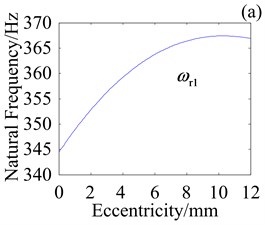
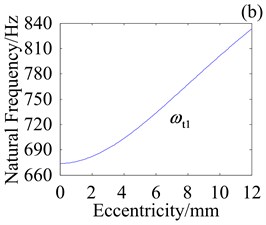
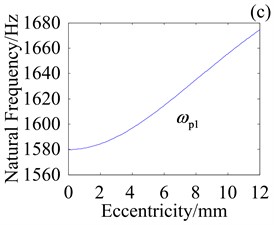
Fig. 11Effect of e on natural frequencies with kHb= 108 N/m
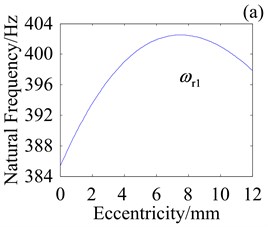
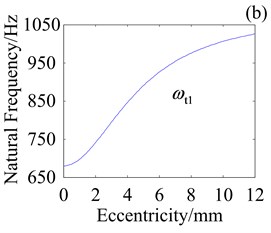
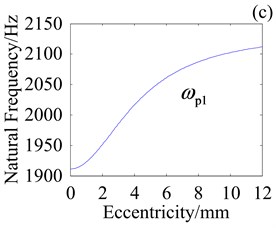
Fig. 10 shows effect of variation in crankshaft eccentricity e on natural frequencies where planet bearing stiffness is 108 N/m. Compared with Fig. 9, decrease in planet bearing stiffness leads to variation in frequency range. Specially, variation in and decrease with decrease in planet bearing stiffness while variation in has little change. It implies that crankshaft eccentricity obviously affects natural frequencies when the planet bearing stiffness is high.
Fig. 11 shows effect of variation in crankshaft eccentricity on natural frequencies where cycloid wheel bearing stiffness is 108 N/m. Compared with Fig. 9, eccentricity has more influence on natural frequencies when is higher. Compared with Fig. 10, effect of eccentricity is more susceptible to with respect to . Hence, suitable design of planet bearing stiffness, cycloid wheel bearing stiffness and crankshaft eccentricity is useful to avoid resonance.
5. Conclusions
RV reducer contains cyclic symmetry and in phase structure. A dynamic model of general description has been developed to investigate the free vibration characteristics and effect of key parameters on natural frequencies. The natural frequencies and vibration modes have highly structured property, which is different from common planetary gears due to RV reducer’s in phase structure. The main results are:
1) All vibration modes can be classified into eleven rotational modes, eleven pairs of translational modes and three or six groups of planetary component modes. Rotational and translational modes have pure rotation and translation of the central components. Only planetary components have motion in planetary component mode.
2) Natural frequencies of rotational mode are independent of the central component transverse support stiffness and mass. Natural frequencies of translational mode are independent of the central component torsional support stiffness and moment of inertia. Natural frequencies of planetary component mode are insensitive to all central component support stiffness, mass and moment of inertia.
3) Crankshaft eccentricity obviously affects natural frequencies when the bearing stiffness is high. Eccentricity affects natural frequencies of planetary mode when only planets and crankshafts have motion.
References
-
Cunliffe F., Smith J. D., Welbourn D. B. Dynamic tooth loads in epicyclic gears. Journal of Manufacturing Science and Engineering, Vol. 96, Issue 2, 1974, p. 578-584.
-
Botman M. Epicyclic gear vibrations. Journal of Manufacturing and Science and Engineering, Vol. 98, Issue 3, 1976, p. 811-815.
-
Frater J., August R., Oswald F. B. Vibration in Planetary Gear Systems with Unequal Planet Stiffness. NASA Technical Report, TM-83428, 1983.
-
Kahraman A. Natural modes of planetary gear trains. Journal of Sound and Vibration, Vol. 173, Issue 1, 1994, p. 125-130.
-
Kahraman A. Planetary gear train dynamics. Journal of Mechanical Design, Vol. 116, Issue 3, 1994, p. 713-720.
-
Lin J., Parker R. G. Analytical characterization of the unique properties of planetary gear free vibration. Journal of Vibration and Acoustics, Vol. 121, 1999, p. 316-321.
-
Lin J., Parker R. G. Structured vibration characteristics of planetary gears with unequally spaced planets. Journal of Sound and Vibration, Vol. 233, Issue 5, 2000, p. 921-928.
-
Wu X., Parker R. G. Modal properties of planetary gears with an elastic continuum ring gear. Journal of Applied Mechanics, Vol. 75, Issue 3, 2008, p. 031014.
-
Parker R. G., Wu X. Vibration modes of planetary gears with unequally spaced planets and an elastic ring gear. Journal of Sound and Vibration, Vol. 329, Issue 11, 2010, p. 2265-2275.
-
Zhu C. C., Xu X. Y., Lim T. C., et al. Effect of flexible pin on the dynamic behaviors of wind turbine planetary gear drives. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 227, Issue 1, 2013, p. 74-86.
-
Bahk C. J., Parker R. G. Analytical solution for the nonlinear dynamics of planetary gears. Journal of Computational and Nonlinear Dynamics, Vol. 6, Issue 2, 2011, p. 021007.
-
Parker R. G., Agashe V., Vijayakar S. M. Dynamic response of a planetary gear system using a finite element/contact mechanics model. Journal of Mechanical Design, Vol. 122, Issue 3, 2000, p. 304-310.
-
Qian P., Zhang Y., Cheng G., et al. Model analysis and verification of 2K-H planetary gear system. Journal of Vibration and Control, 2013, p. 1-12.
-
Ericson T. M., Parker R. G. Planetary gear modal vibration experiments and correlation against lumped-parameter and finite element models. Journal of Sound and Vibration, Vol. 332, Issue 9, 2013, p. 2350-2375.
-
Kahraman A. Free torsional vibration characteristics of compound planetary gear sets. Mechanism and Machine Theory, Vol. 36, Issue 8, 2001, p. 953-971.
-
Guo Y., Parker R. G. Purely rotational model and vibration modes of compound planetary gears. Mechanism and Machine Theory, Vol. 45, Issue 3, 2010, p. 365-377.
-
Kiracofe D. R., Parker R. G. Structured vibration modes of general compound planetary gear systems. Journal of Vibration and Acoustics, Vol. 129, Issue 1, 2007, p. 1-16.
-
Dhouib S., Hbaied R., Chaari F., et al. Free vibration characteristics of compound planetary gear train sets. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 222, Issue 8, 2008, p. 1389-1401.
-
Cooley C. G., Parker R. G. Vibration properties of high-speed planetary gears with gyroscopic effects. Journal of Vibration and Acoustics, Vol. 134, Issue 6, 2012, p. 061014.
-
Cooley C. G., Parker R. G. Mechanical stability of high-speed planetary gears. International Journal of Mechanical Science, Vol. 69, 2013, p. 59-71.
-
Lai T. S. Design and machining of the epicycloid planet gear of cycloid drives. The International of Journal of Advanced Manufacturing Technology, Vol. 28, 2006, p. 665-670.
-
Blagojević M., Nikolić V., Marjanović N., et al. Analysis of cycloid drive dynamic behavior. Scientific Technical Review, Vol. 59, Issue 1, 2009, p. 52-56.
-
Fedosovskii M. E., Aleksanin S. A., Nikolaev V. V., et al. The effect of a cycloid reducer geometry on its loading capacity. World Applied Sciences Journal, Vol. 24, Issue 7, 2013, p. 895-899.
-
Zhang D. W., Wang G., Huang T., et al. Dynamic formulation of RV reducer and analysis of structural parameters. Chinese Journal of Mechanical Engineering, Vol. 37, Issue 1, 2001, p. 69-74, (in Chinese).
-
Zhang Y. H., Xiao J. J., He W. D. Dynamical formulation and analysis of RV reducer. International Conference on Engineering Computation, 2009, p. 201-204.
-
Zhang Y. H., He W. D., Xiao J. J. Dynamical model of RV reducer and key influence of stiffness to the nature character. Third International Conference on Information and Computing (ICIC), 2010, p. 192-195.
Cited by
About this article
The work is based upon work supported by the National High Technology Research and Development Program of China (863 Program) (No. 2011AA04A102).
