Abstract
In allusion to the problem that experimental results of similitude models of a rotating turbine disc predict dynamic characteristics of the prototype, the accurate design method of dynamic similitude models of a rotating thin walled annular plate is investigated by considering the centrifugal stress requirement. The vibration differential equation is employed to deduce geometrically complete scaling laws of dynamic frequency and centrifugal stress. In order to determine accurate distorted scaling laws of dynamic frequency, the sensitivity analysis and determination principle are used. For distorted scaling laws of centrifugal stress, the average approach of candidate distorted scaling laws is proposed, and its mathematical form is simple. Furthermore, the numerical validation indicates that distorted scaling laws can predict dynamic characteristics of the prototype and reflect the strength conditions or even failures of a prototype with good accuracy, and applicable intervals of the distorted scaling law are calculated. Finally, an acceptable procedure of the similitude design method of a rotating thin walled annular plate is provided, which guides to the design of test models considering centrifugal stress requirement.
1. Introduction
Thin walled annular plates are widely applied to the mechanical engineering, for example, the high-speed centrifugal separators due to their excellent dynamic characteristics and high specific stiffness [1-3]. Furthermore, the vibration is one of the most significant investigation in analyzing a thin walled annular plate [4, 5]. However, employing the actual structures directly in experimental tests is difficult to test and time-consuming. Consequently, dynamic similitude models are necessary to predict or reflect dynamic behaviors of a prototype. Nevertheless, for some problems, it is not feasible to fulfill this requirement of complete similitude conditions, leading to geometrically distorted similitude. For example, the thickness of a scaled down model of thin walled annular plates is usually difficult to machine.
The similitude theory of thin walled plates has been studied by many researchers. Qian et al. [6] established the dynamic similitude results of laminated plates, and the similitude models could accurately predict the response. Rezaeepazhand and Simitses [7-9] established the scaling laws of laminated plates between a prototype and a model based on governing equations. In their studies, scaled down models of laminated plates can accurately predict the vibration response of a prototype. Wu et al. [10, 11] built scaling laws of the dynamic responses between a full-size beam and a complete similitude model, both elastically supported at each end and subjected to a moving force were investigated. Singhatanadgid et al. [12, 13] obtained scaling laws for buckling of annular plates subjected to loads and the vibration response of rectangular plates. In their studies, for complete and distorted similitude cases, scaling laws were investigated and validated with numerical tests and experimental results. Oshiro and Alves [14, 15] employed a geometrically distorted model to predict the response of a full-size prototype with loads when models have distorted dimensions and materials, and three problems of a prototype subjected to dynamic loads are analyzed. Ramu et al. [16, 17] built the scaled down models with a different material for elastic structures and analyzed vibration characteristics of the prototype by using a model. In their studies, the established scaling laws are validated by using simple testing problems. Yazdi et al. [18, 19] established a set of scaling laws that can predict the nonlinear natural frequency and flutter of laminated plates, and the effects of distorted models about the number of plies and vibration amplitudes were studied. De Rosa et al. [20] investigated the exact and distorted scaling laws for the analysis of the dynamic response of rectangular flexural plates.
Similitude theory is usually employed to derive the scaling laws based on the governing equation. A different method is developed to obtain approximate scaling laws of thin walled plates and shells by Luo [21-23], where the determination principle and structural size intervals are proposed to predict the natural characteristics and dynamic response. The distorted models of coating thin plates are investigated for predicting the responses, and the effects of different coating thickness and coating forms are discussed by Luo et al. [21]. Particularly in Luo [22, 23], the applicability of determination method of the structural size intervals and the design principles of accurate scaling laws are presented.
From what have been discussed above, there were plenty of theoretical investigations about the dynamic similitude of thin walled plates. However, the similitude design method of a rotating thin walled plates is still rare for considering the dynamic frequencies and centrifugal stresses. In the present work, in order to determine accurate distorted scaling laws of dynamic frequencies, the exact ratio relationship is presented and applied. Furthermore, the geometrical average approach is proposed and validated by numerical tests in order to obtain scaling laws of centrifugal stresses.
2. Vibration differential equation
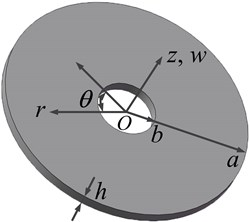
A thin walled annular plate is shown in Fig. 1. is elastic modulus of material, is Poisson’s ratio and is density. is outer radius, is inner radius, and is thickness.
Fig. 1A thin walled annular plate
The governing equation of thin walled annular plates can be written as [24]:
where is Laplace operator:
and is radial displacement; is deflection angle; is the displacement along with direction ; is the bending stiffness of thin walled annular plates, ; is time.
The deflection equation of thin walled annular plates is supposed:
where is the mode function of thin walled annular plates; is the natural frequency.
Substituting Eq. (2) into (1) yields:
3. Complete similitude design method
3.1. Dynamic frequencies
According to Eq. (3), governing equations of the prototype and the model can be expressed as:
where subscript denotes the prototype, subscript denotes the model.
Substitute scaling factor (, , , , , , etc.) into Eq. (4b), yields:
According to similitude theory, the corresponding coefficient of the prototype is proportional to the model in the governing equation, thus:
Due to (), yields:
Under the condition of geometrically complete similitude, which means:
Substitute Eq. (8) into (7), Eq. (7) is rearranged as:
Dynamic frequency of thin walled annular plates can be described as:
where is dynamic frequency; is constant coefficient of dynamic frequency.
Dynamic frequency of the prototype and the model can be expressed as:
Substitute scaling factors (, , ) into Eq. (11b), yields:
Equation should be satisfied in order to obtain accurate complete scaling law. Therefore, geometrically complete scaling law of dynamic frequency can be written as:
3.2. Centrifugal stresses
The centrifugal force is mainly considered when a thin walled annular plate rotates, and centrifugal force of thin walled annular plates can be denoted as:
Therefore, the centrifugal stress of thin walled annular plates on the inner radius’ edge can be obtained as:
The centrifugal stresses of the prototype and model can be expressed as:
Substituting scaling factors (, , , , , , etc.) into Eq. (16b) yields:
According to Eq. (8), Eq. (17) can be written as:
Therefore, geometrically complete scaling law of the centrifugal stress can be obtained as:
4. Distorted corrections
4.1. Dynamic frequencies
There will be many limitations in directly employing geometrically complete similitude models in experiments. For example, the thickness of the scaled down model of thin walled annular plates is usually difficult to machine. Therefore, it is necessary and important to design distorted models in experiments to predict dynamic characteristics of the prototype. Complete scaling laws can be obtained by the method of analyzing governing equations. However, inner radius and outer radius are not directly reflected in the governing Eq. (3), so it is difficult to get distorted scaling laws by directly using the governing equation.
In general, scaling factors and are regarded as independent in distorted scaling laws [22]. Equation can be supposed, where , should satisfy the relationship . Therefore, the distorted scaling law of thin walled annular plates can be expressed as:
A principle [23] is employed to determine the accurate distorted scaling law by combining governing equation and sensitivity analysis. Sensitivity of the structural vibration behavior is defined by the changing rate of vibration characteristic parameters with respect to structural parameters (mass, stiffness and geometrical parameters) [25, 26]. The principle can be described as:
Principle: In the distorted scaling law, the index ratio : is approximate to the sensitivity ratio : , which means:
where and are sensitivity values of the natural frequency with respect to non-dimensional structural parameters, respectively.
Geometrical sizes and material parameters of the prototype are listed in Table 1. By using ANSYS, the dynamic frequency and modes of the prototype are depicted in Table 2, where is circumferential half wave number and is radial wave number.
Table 1Parameters of the prototype
Outer radius / mm | Inner radius / mm | Thickness / mm | Young’s modulus / Pa | Density / kgm-3 | Poisson’s ratio | Angular velocity / rad⋅s-1 |
205 | 35 | 15 | 1.95×1011 | 8000 | 0.3 | 1885 |
Table 2Dynamic characteristics of the prototype
Order i | 1 | 2 | 3 | 4 | 5 | 6 |
Dynamic frequency / Hz | 491.15 | 492.18 | 681.15 | 1198.1 | 1941.9 | 2542.5 |
Modes | 2, 1 | 1, 1 | 4, 1 | 6, 1 | 8, 1 | 1, 2 |
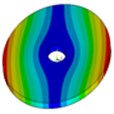 | 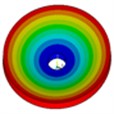 | 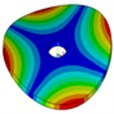 |  |  |  |
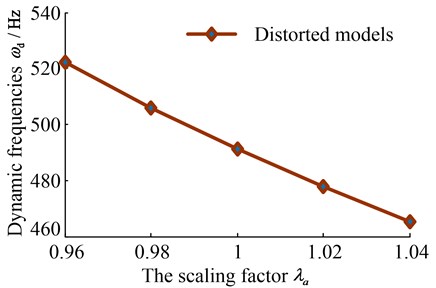
Taking the distorted scaling law of the first order’s natural frequency as an example, the sensitivity value of the first order’s natural frequency with respect to the scaling factor is analyzed and obtained by ensuring other sizes and material parameters unchanged. Furthermore, the first order’s dynamic frequencies of outer radius’ distorted models are shown in Table 3.
Table 3The dynamic characteristics of outer radiuses’ distorted models for modes (2, 1)
Outer radius / mm | Scaling factor | Dynamic frequency / Hz | |
Model 1 | 196.8 | 0.96 | 522.20 |
Model 2 | 200.9 | 0.98 | 505.95 |
Model 3 | 209.1 | 1.02 | 477.65 |
Model 4 | 213.2 | 1.04 | 465.33 |
As indicated in Fig. 2, the curve is fitted by the first order’s natural frequencies and the cubic polynomial equation is:
Fig. 2The fitting curve of natural frequencies of outer radiuses’ distorted models
In this research, adopting the adjusted square to determine the efficiency of fitting curves, the adjusted square can be expressed as:
where is the fitting point number; is order of fitting polynomial; is fitting value; is average value; is true value.
By comparing and analyzing in this research, the fitting curve is thought to be effective and suitable if 0.99.
The adjusted square of the fitting curve is 0.999. So the fitting curve of the first order’s natural frequencies of outer radius’ distorted models is effective.
The sensitivity of the first order’s natural frequencies with respect to outer radius’ scaling factor is:
Similarly, the sensitivity of the first order’s natural frequencies with respect to the scaling factor can be obtained:
As a result of the sensitivity analysis of the thin walled annular plate:
According to the principle, yields:
From Eq. (20), yields:
Solve Eq. (27) and Eq. (28), yields:
Therefore, the distorted scaling law of the first order’s natural frequency can be written as:
According to Eq. (10), should be satisfied in order to determine accurate distorted scaling laws. Under the condition of distorted similitude , the distorted scaling law of dynamic frequency can be obtained as:
4.2. Centrifugal stresses
By comparing Eq. (16a) and (17), there are candidate scaling laws of centrifugal stress, which means:
Let , keeping scaling factor unchanged and is variable. Furthermore, predicted values of centrifugal stresses are calculated and fitted by using Eq. (32), and the fitting curves are shown in Fig. 3.
Fig. 3Predicted values of centrifugal stress
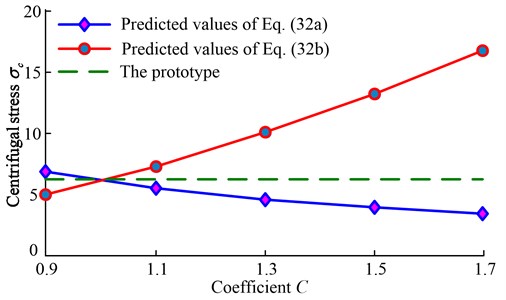
According to the trend of fitting curves in Fig. 3, the geometrical average of Eq. (32) is employed as the distorted scaling law. That is:
Predicted values of centrifugal stresses are obtained and fitted by Eq. (33), and the fitting curves are shown in Fig. 4.
Therefore, the distorted scaling law Eq. (33) can accurately predict the centrifugal stresses of the prototype.
Fig. 4The comparison of predicted centrifugal stress
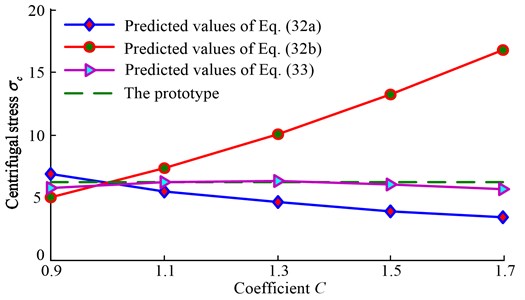
5. Comparison and discussion
5.1. Validation for dynamic scaling laws
Taking the previous six orders’ dynamic frequency of distorted models as examples, illustrate effectiveness of the design method for dynamic distorted models. Finally, an acceptable procedure of determining method of accurate distorted scaling law is given out.
Parameters of the prototype are shown in Table 1. In addition, select a distorted model to validate dynamic scaling laws, geometric sizes and material parameters of the distorted model are shown in Table 4.
Table 4Parameters of the distorted model
Outer radius / mm | Inner radius / mm | Thickness / mm | Young’s modulus / Pa | Density / kgm-3 | Poisson’s ratio | Angular velocity / rad⋅s-1 |
246 | 31.5 | 15 | 1.95×1011 | 8000 | 0.3 | 1206 |
Similarly, analyze the sensitivity of the previous six orders’ natural frequencies with respect to outer and inner radius and distorted scaling laws are shown in Table 5. The error between dynamic frequency of the prototype and predicted values can be denoted as:
As a result of Table 5, errors are within 5 % between dynamic frequencies of the prototype and predicted frequencies of the model, and their modes are coincident. Therefore, distorted scaling laws can accurately predict dynamic characteristics of the prototype.
Finally, the establishment procedure of scaling laws of a rotating thin walled annular plate is summarized:
1) Determine geometrically complete scaling laws of dynamic frequency and centrifugal stress according to the governing equation.
2) According to the governing equation, assume a distorted scaling law for dynamic frequency and centrifugal stress.
3) Analyze the sensitivity of dynamic frequency and determine the dynamic distorted scaling law based on the significant principle.
Table 5Validation for the previous six orders’ distorted scaling laws
Order | Distorted scaling laws | Frequency of prototype / Hz | Frequency of model / Hz | Predicted values / Hz | Modes | Error / % |
1 | 491.15 | 301.74 | 511.42 |  | 4.13 | |
2 | 492.18 | 309.01 | 494.95 |  | 0.56 | |
3 | 681.15 | 444.55 | 689.87 |  | 1.28 | |
4 | 1198.1 | 819.14 | 1186.4 |  | 0.98 | |
5 | 1941.9 | 1345.0 | 1936.8 |  | 0.26 | |
6 | 2542.5 | 1611.3 | 2625.8 |  | 3.28 |
5.2. Applicable interval for strength scaling laws
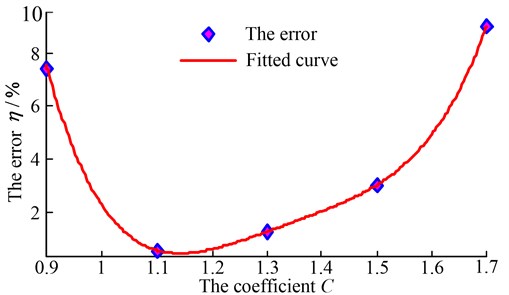
When distorted models accurately predict the strength of the prototype, the error needs to be within 5 % between the prototype and predicted values. So the applicable interval of distorted scaling laws for centrifugal stress is necessary. In order to obtain the applicable interval of the distorted scaling law of centrifugal stress, distorted models with different coefficient are selected in Eq. (33). Errors are calculated by Eq. (34) and shown in Table 6 between the prototype and predicted values.
Table 6Errors between the prototype and predicted values
Scaling factor | Coefficient | Centrifugal stress of models / ×108Pa | Predicted values / ×108Pa | Errors / % | |
Model 1 | 1.2 | 0.9 | 7.17 | 5.76 | 7.40 |
Model 2 | 1.2 | 1.1 | 10.5 | 6.26 | 0.58 |
Model 3 | 1.2 | 1.3 | 14.5 | 6.30 | 1.28 |
Model 4 | 1.2 | 1.5 | 19 | 6.03 | 3.03 |
Model 5 | 1.2 | 1.7 | 24.1 | 5.66 | 8.99 |
In addition, the error curve shown in Fig. 5 is fitted by errors of Table 6, and the fifth degree polynomial equation is:
The adjusted square of the fitting curve shown in Fig. 5 is 1. So the error fitting curve is effective.
When [0.9, 1.7], let 5 %, solutions of the fitting Eq. (35) can be expressed as: 0.91, 1.65. Therefore, the structural size interval of the coefficient can be denoted as: [0.91, 1.65]. The distorted scaling law of centrifugal stress can accurately predict the strength of the prototype when the coefficient of Eq. (35) is included in [0.91, 1.65].
Fig. 5The error fitting curve
6. Conclusions
This study established dynamic similitude models of a rotating thin walled annular plate considering centrifugal stress requirement. Firstly, scaling laws of the dynamic frequency and centrifugal stress of geometrically complete similitude models were derived based on the governing equation. For distorted similitude cases of dynamic frequency, in order to obtain the accurate scaling law of dynamic frequency, the exact ratio relationship and sensitivity analysis are combined. Furthermore, the distorted scaling law of centrifugal stresses is practical in engineering applications by geometrical average method. In addition, the numerical validation demonstrated complete and distorted similitude models can predict dynamic characteristics and reflect the strength condition, or even failures of the prototype with good accuracy. Detailed conclusions are listed as following:
1) According to the governing equation, complete scaling laws of the dynamic frequency and centrifugal stress of a rotating thin walled annular plate were established.
2) In order to determine accurate distorted scaling laws of dynamic frequency, the ratio relationship was presented and applied.
3) The geometrical average approach is proposed in order to obtain the distorted scaling law of centrifugal stresses, and the applicable interval of the distorted scaling law was established in [0.91, 1.65].
References
-
Qin Z. Y., Yan S. Z., Chu F. L. Influence of clamp band joint on dynamic behavior of launching system in ascent flight. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Vol. 228, Issue 1, 2014, p. 97-114.
-
Yao M. H., Chen Y. P., Zhang W. Nonlinear vibrations of blade with varying rotating speed. Nonlinear Dynamics, Vol. 68, Issue 4, 2012, p. 487-504.
-
Yao M. H., Zhang W. Using the extended Melnikov method to study multi-pulse chaotic motions of a rectangular thin plate. International Journal of Dynamics and Control, Vol. 2, Issue 3, 2014, p. 365-385.
-
Wang X., Striz A. G., Bert C. W. Free vibration analysis of annular plates by the DQ method. Journal of Sound and Vibration, Vol. 164, Issue 1, 1993, p. 173-175.
-
Wang H. J., Chen Y. R., Chen L. W. Finite element dynamic analysis of rotating orthotropic sandwich annular plates. Composite Structures, Vol. 62, Issue 2, 2003, p. 205-212.
-
Qian Y., Swanson S. R. Experimental measurement of impact response in carbon/epoxy plates. AIAA Journal, Vol. 28, Issue 6, 1990, p. 1069-1074.
-
Simitses G. J., Rezaeepazhand J. Structural similitude and scaling laws for buckling of cross-ply laminated plates. Journal of Thermoplastic Composite Materials, Vol. 8, Issue 3, 1995, p. 240-251.
-
Rezaeepazhand J., Simitses G. J. Use of scaled-down models for predicting vibration response of laminated plates. Composite Structures, Vol. 30, Issue 4, 1995, p. 419-426.
-
Rezaeepazhand J., Simitses G. J. Design of scaled down models for predicting shell vibration response. Journal of Sound and Vibration, Vol. 195, Issue 2, 1996, p. 301-311.
-
Wu J. J., Cartmell M. P., Whittaker A. R. Prediction of the vibration characteristics of a full-size structure from those of a scale model. Computers and Structures, Vol. 80, Issue 18, 2002, p. 1461-1472.
-
Wu J. J. The complete-similitude scale models for predicting the vibration characteristics of the elastically restrained flat plates subjected to dynamic loads. Journal of Sound and Vibration, Vol. 268, Issue 5, 2003, p. 1041-1053.
-
Singhatanadgid P., Ungbhakorn V. Scaling laws for buckling of polar orthotropic annular plates subjected to compressive and torsional loading. Thin-Walled Structures, Vol. 43, Issue 7, 2005, p. 1115-1129.
-
Singhatanadgid P., Songkhla A. N. An experimental investigation into the use of scaling laws for predicting vibration responses of rectangular thin plates. Journal of Sound and Vibration, Vol. 311, Issue 1, 2008, p. 314-327.
-
Alves M., Oshiro R. E. Scaling impacted structures when the prototype and the model are made of different materials. International Journal of Solids and Structures, Vol. 43, Issue 9, 2006, p. 2744-2760.
-
Oshiro R. E., Alves M. Predicting the behavior of structures under impact loads using geometrically distorted scaled models. Journal of the Mechanics and Physics of Solids, Vol. 60, Issue 7, 2012, p. 1330-1349.
-
Raja V. P., Ramu M., Thyla P. R. Analytical and numerical validation of the developed structural similitude for elastic models. Indian Journal of Engineering and Materials Sciences, Vol. 20, 2013, p. 492-496.
-
Ramu M., Raja V. P., Thyla P. R. Establishment of structural similitude for elastic models and validation of scaling laws. KSCE Journal of Civil Engineering, Vol. 17, Issue 1, 2013, p. 139-144.
-
Yazdi A. A., Rezaeepazhand J. Accuracy of scale models for flutter prediction of cross-ply laminated plates. Journal of Reinforced Plastics and Composites, Vol. 30, Issue 1, 2011, p. 45-52.
-
Yazdi A. A. Study nonlinear vibration of cross-ply laminated plates using scale models. Polymer Composites, Vol. 35, Issue 4, 2014, p. 752-758.
-
De Rosa S., Franco F., Meruane V. Similitudes for the structural response of flexural plates. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2015, (in Press).
-
Zhu Y. P., Luo Z., Zhao X. Y., Han Q. K. Determination method of the structure size interval of dynamically similar models for predicting vibration characteristics of the coated thin plates. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 229, Issue 1, 2014, p. 59-68.
-
Luo Z., Zhao X. Y., Zhu Y. P., Li J. Z. Determination method of the structure size interval of dynamic similar models for predicting vibration characteristics of the isotropic sandwich plates. Journal of Vibroengineering, Vol. 16, Issue 2, 2014, p. 608-622.
-
Luo Z., Wang Y., Zhu Y. P., Wang D. Y. The dynamic similitude design method of thin walled structures and experimental validation. Shock and Vibration, 2016, p. 6836183.
-
Soedel W. Vibrations of Shells and Plates. Second Edition. Marcel Dekker Inc., New York, 1993.
-
Lee I. W., Jung G. H. An efficient algebraic method for the computation of natural frequency and mode shape sensitivities – Part I. Distinct natural frequencies. Computers and Structures, Vol. 62, Issue 3, 1997, p. 429-435.
-
Lee I. W., Jung G. H. An efficient algebraic method for the computation of natural frequency and mode shape sensitivities – Part II. Multiple natural frequencies. Computers and Structures, Vol. 62, Issue 3, 1997, p. 437-443.
About this article
This work was supported by the National Science Foundation of China (Grant Number 11572082); the Fundamental Research Funds for the Central Universities of China (Grant Number N140301001); the Key Laboratory for Precision and Non-traditional Machining of Ministry of Education, Dalian University of Technology (Grant Number JMTZ201602); and the Excellent Talents Support Program in Institutions of Higher Learning in Liaoning Province of China (Grant Number LJQ2015038).
