Abstract
The present work develops a novel procedure of establishing an amplitude-dependent time series model for a nonlinear system and estimating the instantaneous modal parameters of the system from the dynamical responses. The undetermined coefficient in an amplitude-dependent autoregressive with exogenous input (amplitude-dependent ARX) model are assumed as functions of amplitude and are expanded by shape functions constructing by moving least-squares with polynomial basis functions. The amplitude of dynamical responses could be obtained by Hilbert transform. The instantaneous modal parameters of the system are directly estimated from the coefficient in the amplitude-dependent ARX model. The feasibility of the procedure is demonstrated by processing numerically simulated dynamic responses of a nonlinear system. The proposed scheme is demonstrated to be superior to time-varying ARX model and recursive method in identifying modal parameters. Finally, the proposed approach is applied to process measured data for a frame specimen subjected to a series of base excitations in shaking table tests. The specimen was damaged during testing. The identified modal parameters are consistent with observed physical phenomena.
1. Introduction
In most identification methods for real system the model structure has been assumed beforehand such as linear system, time-varying system and nonlinear system. The linear system identification ARX (AutoRegressive with eXogenous inputs), ARMAX (AutoRegressive and Moving Average with eXogenous inputs) and OE (Output Error) models have been extensively studied [1-4]. However, many practical examples of nonlinear dynamic behavior have been reported in the engineering literature. In mechanical and civil engineering, a system with active control devices [5-9] modifying stiffness or damping is a time-varying system. A structure under damage normally exhibits nonlinear dynamic behaviors and time-dependent stiffness and damping [10, 11]. Variations in system stiffness and damping over time result in time-varying modal parameters of the system. Consequently, determining modal parameters of a time-varying system or nonlinear system is generally very useful when assessing structural damage in real applications. The linear parameter estimation technique has been employed [4] for these nonlinear identifications. There are, however, few practical identification methods for nonlinear systems from input-output data. Several theoretical studies have been done for the identification of the nonlinear system represented by a linear in the parametric model with nonlinear functions [12, 13, 14].
The amplitude-dependent autoregressive with exogenous input (AD-ARX) model is often utilized to establish an input–output relationship of a nonlinear system from its dynamic responses and input forces [15]. To identify the dynamic characteristics of nonlinear structures from the ambient vibration, free vibration, and earthquake response data, this study develops a unified procedure by extending, with some modification, the amplitude-dependent ARX model by Hilbert transform to obtain the function of amplitude. Furthermore, to demonstrate the feasibility of the proposed procedure, the procedure is applied to process a simulated nonlinear vibration model, and measured data for a frame specimen subjected a series of base excitations in shake table test. The specimen showed strong nonlinear dynamic behaviors because the damage occurred during testing.
2. Methodology
The nonlinear structural system encountered in civil and mechanical engineering can be described by the following equations of motion:
where , and are mass, damping and stiffness matrices, respectively, and and are functions of amplitude of responses, while and are displacement and force vectors, respectively. A building may behave nonlinearly when subjected to a large earthquake, and its and are functions of amplitude of responses. Consequently, the instantaneous modal parameters of the building change with amplitude of responses in each time step. One can easily judge whether a building is damaged or not in an event from the instantaneous natural frequencies obtained from dynamic responses of the building under the event.
The equations of motion in a discrete form are equivalent to:
where and are the vectors of measured responses and input forces at time , respectively; is the sampling rate of the measurement, and are matrices of the coefficient functions to be determined in the model, and is a vector representing the residual error accommodating the effects of measurement noise, modeling errors and unmeasured disturbances. Equation (2) is known as amplitude-dependent ARX model. The measured displacement responses are used for to ensure that instantaneous modal parameters can be directly identified from without a systematic error [16].
Following the method proposed by Huang et al. [16], each coefficient function in and is linearly expanded by the so called shapes functions constructed by a set of basis functions, which are polynomials herein, through a moving least-squares approach [17]. Let and denote () element of and , respectively, and they are expressed as:
where is a vector of shape functions, , ,, , is a weight function; is the amplitude of dynamic responses that would obtained by Hilbert transform; is the number of nodal points used for each coefficient function, and are two unknown vectors of coefficients for and , respectively. Many weight functions can be used in the above formulation [18]. In this work, the exponential weight function is applied:
where is the support of the weight function.
A least-squares approach is applied to determine and by minimizing:
where is the number of data points to be used in establishing the amplitude-dependent ARX model. Then, one can obtain the following equation through typical and lengthy mathematical manipulation:
where:
and denotes the Kronecker product. After determining and substituting them into Eq. (3), one obtains . Then, like determining modal parameters from an ARX model, one can obtain the instantaneous modal parameters of the nonlinear system from . A matrix is constructed from as follows:
where is a zero matrix and is an unit matrix. Then, the instantaneous modal parameter (nature frequencies, damping ratios and mode shapes) of the structure can be estimated from the instantaneous eigenvalues and eigenvectors of . Let and represent the kit instantaneous eigenvalue and eigenvector of at reponses amplitude , respectively. The instantaneous eigenvalue is normally a complex number, and is set as . The instantaneous frequency and damping ratio of the system are computed, respectively, by:
where:
The th instantaneous mode shape can be determined from the following the procedure of Huang (2001) [19].
3. Numerical verification
Numerical simulation responses of a Duffing oscillator system were processed to demonstrate the accuracy and effectiveness of the proposed approach in determining instantaneous modal parameters of the nonlinear system. The Duffing oscillator system was shown as follows:
where, 0.05 and . The Runge-Kutta method with a time increment () equal to 0.004 seconds was applied to determine the dynamic responses of this Duffing oscillator system subjected to base excitation.
Assumed the homogeneous solution of this Duffing equation is , then substituted into equation (8) one could obtain:
Using Triple-angle formula and rearranging the above equation, one obtain:
Applying Hilbert transform to Eq. (12), one have:
Here we consider the response of the Duffing oscillator to a weak forcing, then and combining Eq. (13) and Eq. (14), we get:
By solving characteristic polynomial and according the condition of . Besides, imaginary term assigned to magnitude of Euler’s formula, one could get the amplitude-frequency relationship:
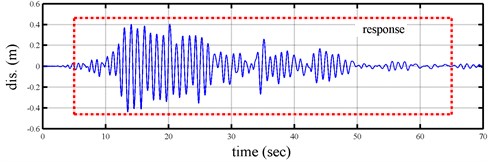
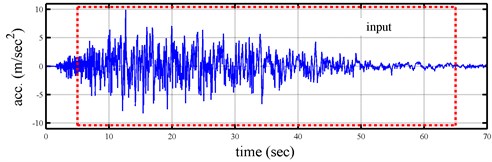
Figure 1 depicts the time histories of input ground acceleration and displacement response of this Duffing equation. One can establish an appropriate amplitude-dependent ARX model from these inputs and responses by employing the formulation given in the preceding section. The identified instantaneous natural frequencies and modal damping ratios are shown in Figure 2, which also demonstrates the excellent agreement between the identified results and the true values. The maximum differences between the identified natural frequencies by AD-ARX model and the true ones are slightly more than 1 %, while the identified modal damping ratios by amplitude-dependent ARX model differs from the true values by slightly more than 5 %.
Fig. 1Time histories of base excitation and simulated displacement response
To demonstrate further the superiority of the present approach to another method in the literature, Figure 2 shows the time-variant parameters that identified by time-varying autoregressive with exogenous input (time-varying ARX) model [16] and recursive method. The formula of TV-ARX in a similar as the AD-ARX expect that the model coefficient of former is function of time, while the model coefficient of latter is function of amplitude. In here, time-varying coefficient of time-varying ARX model was expanded by low-order polynomial function of time.
Fig. 2Instantaneous modal parameters identified from response
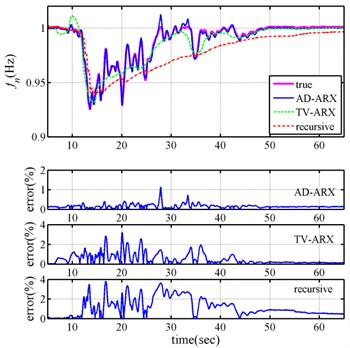
a)
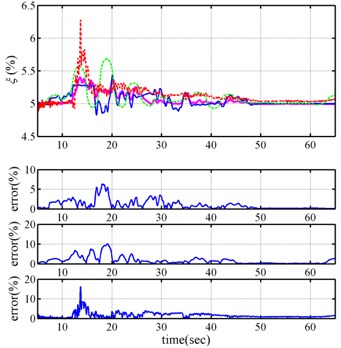
b)
Figure 2 discovers that the maximum differences between the identified natural frequencies by time-varying ARX model and the true ones are about 3 %, while the identified modal damping ratios by time-varying ARX model differ from the true values by slightly more than 10 %. And the maximum differences between the identified natural frequencies by recursive method and the true ones are about 4 %, while the identified modal damping ratios by resursive method differ from the true values by slightly more than 15 %. Comparison of the results in Figure 2 clearly reveals that the amplitude-dependent ARX model outperforms time-varying ARX model and recursive method in correctly identifying the instantaneous modal parameters of nonlinear system.
4. Application
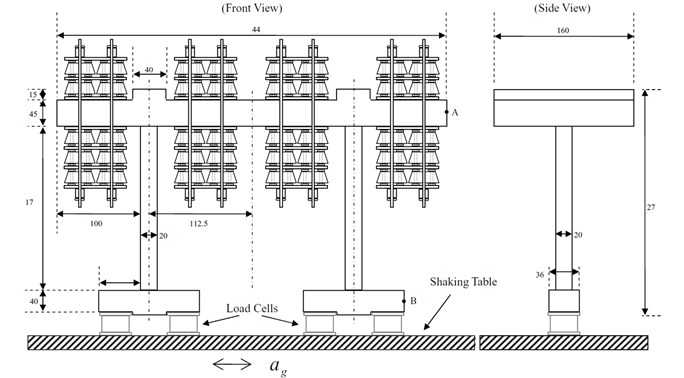
Shaking table tests are vital to understanding the dynamic behavior, especially nonlinear behaviors, of structural systems under earthquakes. The National Center for Research on Earthquake Engineering in Taiwan conducted a series of test on reinforced concrete (RC) frames of two columns interconnected by a strong beam to investigate the dynamic behaviors of low-ductility RC columns and to understand their collapse mechanism. Figure 3 shows the dimensions of the typical frame and the test setup. In total, 21 tons of lead ballast were added to the beam to simulate axial loads on first-story columns in a typical four-story building in Taiwan. Accelerometers and linear displacement transducers were installed at appropriate locations to measure acceleration and displacement responses of a specimen. Load cells were installed between the specimen and shaking table to measure base shear forces.
Fig. 3A sketch of experiment setup
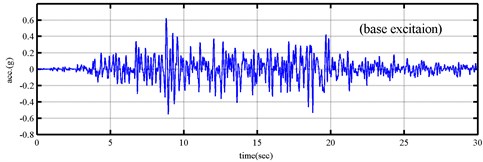
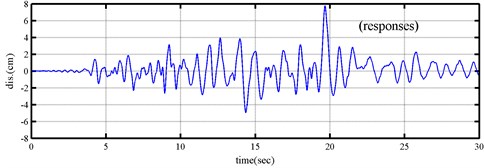
The specimen was subjected to a series of base excitation inputs; that is, it was first shaken under white noise input with small amplitude to estimate its modal parameters. The test is denoted as “before-damage” test because the specimen was not damaged. Then, the specimen was subjected to an earthquake input recoded during the 1999 Chi-Chi earthquake in Taiwan. Strong nonlinear behaviors observed during this test, and columns near beam connection were damaged. The test is denoted as “during-earthquake” test. Finally, the specimen was shaken again with a low-level white noise input, which is denoted as “after-damage” test. Figure 4 shows the acceleration input and displacement response histories during the earthquake test.
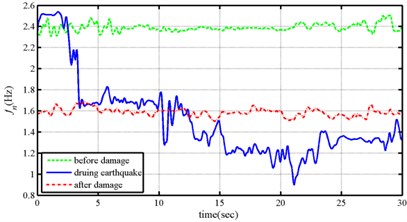
As expected, small variations of instantaneous natural frequencies with time were observed for the cases with white noise input as no further damage occurred under such small input excitation forces. The identified instantaneous natural frequencies in the “before-damage” test are larger than those obtained from the “after-damage” test; the trend is opposite from the identified instantaneous modal damping ratio. The instantaneous natural frequencies from the “during-earthquake” test are close to those identified from the “before-damage” test when 2 seconds as no damaged existed for this duration in the “during-earthquake” test. The value of frequency decreased dramatically around 3 seconds, which likely indicates specimen damage. As the displacement magnitude gradually increases over time to 21.5 seconds, the identified frequency value generally decreases to 0.9 Hz and damping ratio increase to 41 % from less than 10 %. These observations obey the well-known physical phenomenon suggestion that structural damage decreases the natural frequency and increases the damping ratio of a structure.
Fig. 4The input acceleration and response histories from during earthquake test
a)
b)
Fig. 5Instantaneous modal parameters identified from the responses under the Chi-Chi earthquake
a)
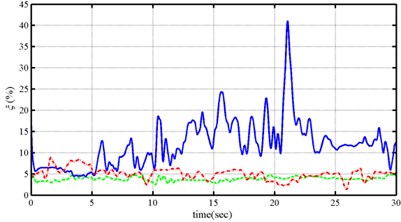
b)
5. Conclusions
This work presented a novel approach for identifying the instantaneous parameters of a building based on the amplitude dependent ARX models. The instantaneous natural frequencies of structural are accurately determined from the coefficient functions of amplitude dependent ARX models, which are expanded by MLS shape functions of amplitude which constructed through Hilbert transform and established from the acceleration responses of the base and the displacement responses of structures.
The proposed approach was demonstrated on a nonlinear Duffing equation under earthquake excitation. A nonlinear system with nonlinear stiffness was considered. The proposed approach was validated by successfully identifying modal parameters by processing numerically simulated responses. Comparing the results obtained by the proposed approach with the coefficient functions of TV-ARX models are expanded by MLS shape functions of time and resursive method that the present approach is substantially superior to these methods in identifying instantaneous modal parameters for nonlinear system.
To demonstrate the applicability of the proposed approach to real data, responses to shaking table tests were processed. The specimen was subjected to a series of base excitation inputs. The specimen was first shaken under white noise input with small amplitude, then subjected to a large earthquake input and damaged, and finally shaken under a small amount of white noise input again. The trend in variations of the identified instantaneous modal parameters is consistent with the observed physical phenomena during the tests. Changes to instantaneous modal parameters due to structural damage can be applied to develop useful criteria for assessing damage of real structures.
References
-
Goodwin G. C., Payne R. L. Dynamic system identification: experiment design and data analysis. New York, Academic Press, 1977.
-
Soderstrom T., Stoica P. System identification: international series in systems and control engineering. Prentice-Hall, 1989.
-
Walter E., Pronzato L., Norton J. Identification of parametric models from experimental data. Communications and control engineering. Springer-Verlag, Berlin, Prentice Hall, 1997.
-
Ljung L. System identification: theory for the user: prentice hall information and system sciences series. 2nd Ed., Prentice Hall, 1999.
-
Saleh A., Adeli H. Parallel algorithms for integrated structural and control optimization. Journal of Aerospace Engineering, Vol. 7, 1994, p. 297-314.
-
Adeli H., Saleh A. Optimal control of adaptive/smart bridge structures. Journal of Structural Engineering, Vol. 123, 1997, p. 218-226.
-
Adeli H., Kim H. Wavelet-hybrid feedback least mean square algorithm for robust control of structures. Journal of Structural Engineering, Vol. 130, 2004, p. 128-137.
-
Kim H., Adeli H. Hybrid feedback-least mean square algorithm for structural control. Journal of Structural Engineering, Vol. 130, 2004, p. 120-127.
-
Jiang X., Adeli H. Dynamic fuzzy wavelet neuro emulator for nonlinear control of irregular highrise building structures. International Journal for Numerical Methods in Engineering, Vol. 74, 2008, p. 1045-1066.
-
Adeli H., Jiang X. Dynamic fuzzy wavelet neural network model for structural system identification. Journal of Structural Engineering ASCE, Vol. 132, 2006, p. 102-111.
-
Jiang X., Mahadevan S., Adeli H. Bayesian wavelet packet denoising for structural system identification. Structural Control and Health Monitoring, Vol. 14, 2007, p. 333-356.
-
Knapp C. H., Pal P. K. Parameter identification in a class of nonlinear systems. IEEE Trans. on Automatic Control, Vol. 28, 1983, p. 497-503.
-
Sjoberg J., Zhang Q., Ljung L., Benveniste A., Delyon B.,Glorennce P. V., Hjalmarsson H., Juditsky A. Nonlinear black-box modeling in system identification: a unified overview. Automatica, Vol. 31, 1995, p. 1691-1724.
-
Li K., Peng J. X., Irwin G. W. A fast nonlinear model identification method. IEEE Trans. Automatic Control, Vol. 50, 2005, p. 1211-1216.
-
Haggan V., Ozaki T. Modeling nonlinear random vibration using an amplitude-dependent autoregressive time series model. Biometrika, Vol. 68, 1981, p. 189-196.
-
Huang C. S., Hung S. L., Su W. C., Wu C. L. Identification of time-variant modal parameters using TVARX and low-order polynomial function. Computer-Aided Civil and Infrastructure Engineering, Vol. 24, 2009, p. 470-491.
-
Lancaster P., Salkauskas K. Curve and surface fitting – an introduction. NY, Academic Press, 1990.
-
Liu G. R. Mesh free methods: moving beyond the finite element method. NY, CRC Press, 2003.
-
Huang C. S. Structural identification from ambient vibration measurement using the multivariate AR model. Journal of Sound and Vibration, Vol. 241, 2001, p. 337-359.
About this article
The authors would like to thank the National Science Council of the Republic of China, Taiwan, for financially supporting this research under Contract No. NSC 101-2218-E-492-006.
