Abstract
In this paper, a nonlinear torsional vibration model with meshing errors, time varying meshing stiffness, damping coefficients and gear backlashes was established and dimensionless equations of the system are derived in the planetary gear train processing device. The paper analyzed the nonlinear dynamic behavior of the device which was used to machine the Circular-Arc-Tooth-Trace cylindrical gear. By using the method of numerical integration, the bifurcation diagrams are obtained and the results indicate that the processing device has abundant bifurcation characteristics with the change of the dimensionless speed, and the damping ratios, gear backlashes and meshing errors of meshing pairs could influence the vibration greatly. The bifurcation diagrams reveal that increasing the damping ratios can change the bifurcation and the chaos can be avoid when the damping ratios are bigger enough, reducing the gear backlashes can reduce the dimensionless displacement amplitudes, increasing the meshing errors can make the bifurcation diagrams shift left for a distance, and alternating load torque with large amplitude will cause complex chaos phenomenon. The study can help to avoid the fatigue failure and instabilities caused by chaos and it also contribute to improving the performance of the processing device.
1. Introduction
The planetary gear processing device was used to machine the CATT gear because it had many advantages, such as large torque-to-weight ratio, large transmission ratios, reduced vibrations and noise as well as high efficiency [1]. These characteristics make sure that the CATT gears have higher machining accuracy. So it is very important to investigate the vibration characteristics of the CATT gear processing device.
At present, although many researchers have investigated the transmission characteristics of the normal planetary gear train and the dynamic characteristics of planetary gear reducer, few research methods can be used to study the CATT gear processing for the vibration model of the processing device is different from the previous studies. The device consists of three or more planetary gear sets and it has translational and rotary motions which can form the ideal tooth profile of the CATT gear [2]. In order to reducing the system vibration which will be influence the correct manufacturing of the tooth profile, this paper has established the vibration model for the processing device.
There are many research papers about the vibration of the planetary gear train in recent decades. But most of the published planetary gear train dynamic models were limited to the normal planetary gear system such as the 2K-H planetary gearbox. Early models were of linear time-invariant type and model summation techniques were used to predict the natural modes and the force responses [3-6], such as A. Kahraman analyzed the natural modes of planetary gears [4]. He used a family of torsional dynamic models of compound gear sets to predict the free vibration characteristics under different kinematic configurations resulting in different speed ratios with a linear model [5]. J. Lin and R. G. Parker also investigated the natural frequency and vibration mode sensitivities to system parameters for both tuned and mistuned planetary gears [7, 8].Afterwards some studies have shown that the gear trains should be modeled as nonlinear systems including periodically varying parameters and backlash [6, 9]. The references [10, 11, 12] investigated the time-varying mesh stiffness and clearance influences. J. Lin and R. G. Parker also studied the structured vibration characteristics of planetary gears with unequally spaced planets [13]. Moreover, Robert G. Parker examined the effectiveness of planet phasing to suppress planetary gear vibration in certain harmonics of the mesh frequency based on the physical forces acting at the sun-planet and ring-planet meshes [14].Several years later, R. G. Parker et al. analyzed vibration modes of planetary gears with unequally spaced planets and an elastic ring gear [15]. Sun Zhimin et al. used a clearance-type nonlinear dynamic model of a 2K-H planetary gear train to analyze the nonlinear dynamic behavior [16]. The paper indicated that the backlash would induce complicated nonlinear dynamic behavior. Li Tongjie et al. also established a nonlinear torsional vibration model with transmission errors, time varying stiffness and gear backlashes. His paper revealed that the system’s motion state would change into chaos and a smaller damping coefficient would cause complex motion in the vibration system [17].
Recently, Chang-Jian and Chen investigated nonperiodic and chaotic responses of flexible rotors supported by various bearings [18, 19]. They provided a useful method to prevent an undesirable motion of the rotor and to reduce the vibration [6]. Similarly, the transmission errors, the spacing and back-lash-related nonlinear dynamics were mainly investigated in planetary gear system in the reference [20] and [21]. However, these vibration models were all based on the conventional planetary gear trains. So the new vibration model need to be established and the nonlinear dynamic behaviors and bifurcation and chaos characteristics of a translational planetary gear train need further investigate.
This study proposed a planetary gears device whose planetary gear center could move with translational motion and established a nonlinear torsional vibration model. The model included the transmission errors, time varying meshing stiffness, damping coefficients and gear backlashes. By using the method of varying-step numerical integration, the nonlinear dynamic behavior of spur planetary gears in the processing device was investigated. The influences of damping coefficient, dimensionless excitation frequency and dimensionless backlash on the vibration model were also investigated by calculating dynamic bifurcation diagrams. This paper tries to improve the stability of the CATT gear processing device by examining the bifurcation and chaos traits of the system.
2. Modeling methodolgy
The structures of the processing device of the CATT gear are shown in Fig. 1. The planetary gear train processing device consists of a sun gear (s), () inside planetary gears (q), outside planetary gears (p) and a carrier (c) without ring gear [22]. The redius of carrier can be regulated by a adjusting nut. Fig. 1 are the 3D models of the CATT gear and its processing device with four gear sets, and these gear sets have to be evenly distributed around the sun gear. All gears are spur gears and the motion of the sun gear is constrained. Each element has one rotational degree-of-freedom.
To establish the mathematical model of the system, a number of assumptions are employed as follows [6]:
1. Each gear body is assumed to be rigid, and the flexibilities of the gear teeth at each gear mesh interface are modeled by a spring with periodically time-varying stiffness. What’s more, this mesh stiffness is influenced by a clearance element representing gear backlash.
2. Excepting the sun gear, each gear and carrier are assumed to rotate along their bearings only.
3. Each inside planet and outside planet on the planet carrier distributes uniformly with the same parameters.
4. Each gear set has same meshing error and damping coefficient.
The planetary gear dynamic model is based on the one developed by Lin and Parker [8, 12]. But the structure of the model is different from the previous papers. According to the motion properities of the CATT gear device and the assumptions, the vibration system can be modeled a spring-damping vibration system with meshing errors and gear backlashes and the model is shown in Fig. 2.
Fig. 1The CATT gear and its planetary gear train processing device
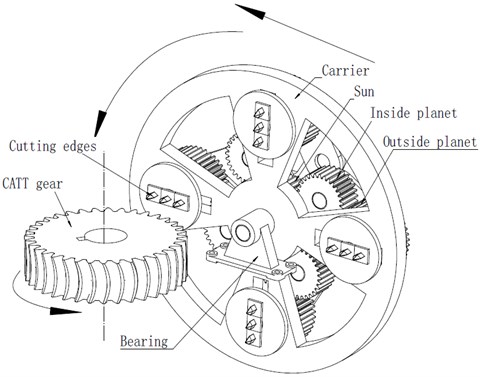
Fig. 2Torsional vibration model of planetary gears
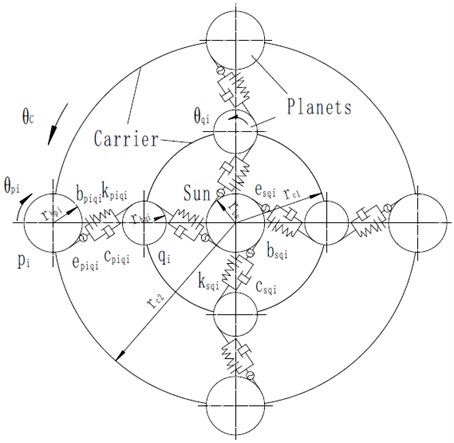
The model is normally selected four gear sets for vibration analysis. Rotational motion of the carrier is denoted by . Similarly, the rotational motions of the inside planets and outside planets are denoted by and , , where indicates the number of planets. Their moments of inertia can be expressed by , , (). Not noly the tooth meshes between sun and inside planet but also the tooth meshes between the inside planet and the outside planet are modelled as linear springs with time-varying stiffnesses , (). Simultaneously, the paper considered the non-linear factors such as the damping , , clearance , and meshing error , to establish a complete model as shown in Fig. 2. By using the Lagrange equation, the system’s equations of motion are:
where , and the parameters , , , are the base circle radii of the sun, inside planets and outside planets respectively. is the radius of the circle passing through the inside planets centers for the carrier and is the radius of the circle passing through the outside planets centers for the carrier. These parameters are shown in Fig. 2. Moreover, , , , are the masses of the sun gear, inside planet gear, outside planet gear and carrier. There are three external torques in the processing device system. is input torque, and are load torques. and are the elastic meshing forces [16]. They can be expressed as:
where is the non-linear function of backlash and it can be represented by [23]:
For spur gears, rectangular waves are often used to approximate mesh stiffness [12]. Each mesh stiffness can be represented by:
where , () are mean values and , () are time-varying components of the gear meshes. is the mesh frequency of the sun-planet and , () are the phases.
, are the viscous meshing forces and they can be expressed as [16]:
where , are the damping coefficients and they can be expressed as [16]:
where is the damping ratio of meshing pair for the sun to the inside planetary gear, and is the damping ratio of meshing pair for the inside planet to the outside planet. , , , are the equivalent masses of the sun, planets and carrier. , are the gear backlashes and can be represented by [16]:
where , are the synthetical meshing errors and , are the phase angles.
In order to eliminate the displacement of rigid body, the generalized coordinates are introduced as:
In order to simplify the solutions of the equations we use dimensionless variables, introducing the parameters:
where is dimensionless time and is nominal size of displacement. The dimensionless displacement, velocity, and acceleration are representatives of , , and .
Substituting equations Eq. (2), Eq. (5) and Eq. (8) into Eq. (1) and we obtain equations as:
where , , , can be expressed as:
where , , , , can be represented by:
In order to investigate the effect of the external noise on the vibration system, the load torques and can be expressed as following:
where and are the average torques of and respectively, and are external noises of the load torques, , is the angular velocity of the external noises, and are the phase angles, in general, .
3. The analysis of the bifurcation characteristics
This paper investigated the vibration characteristics of the planetary gear processing device by using a set of basic parameters. The system parameters are listed in Table 1 and the calculation parameters are given in Table 2. What’s more, the other parameters are set as , .
Table 1System parameters of the planetary gear processing device
Parameter | Sun | Inside planet | Outside planet | Carrier |
Number of teeth | 40 | 30 | 40 | - |
Module (mm) | 3 | 3 | 3 | - |
Pressure angle (°) | 20 | 20 | 20 | - |
Tooth width (mm) | 15 | 15 | 15 | - |
(mm) | 56.38 | 42.29 | 56.38 | 105&210 |
- | 7.13e-4 | 0.002 | 7.58e-3 |
Table 2Calculation parameters of the planetary gear processing device
Parameter | Value | Parameter | Value |
(N/m) | 0.825e9 | (mm) | 0.01 |
(N/m) | 1.0e9 | 4 | |
, (N/m) | 0.2e9 | (Nm) | 1500 |
, (mm) | 0.01 | (Nm) | 600 |
, (mm) | 0.05 | (Nm) | 900 |
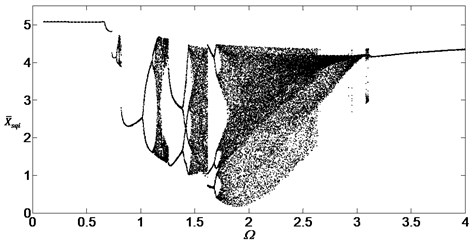
The paper used numerical integration algorithm to solve the non-linear Eq. (10) with four order Runge-Kutta method and investigated the steady state responses of the planetary gear system. First of all, we investigated the vibtation system without considering the external noises, so the parameters are set at The bifurcation diagram of the system with the non-dimensional speed is shown in Fig. 3 when the damping ratios are at .
Fig. 3 shows that the system is stable before the critical speed and the dynamic behavior of the system is found to be a periodic motion, then the system will pass through the chaotic regions and the single periodic regions. The dynamic behavior is found to be -periodic motion at . Then the system will be in the second chaotic region. Simultaneously, when the non-dimensional speed is at , the dynamic behavior is a -periodic motion. As the non-dimensional speed further increaases, the dynamic behavior of the system transits to nonperiodic motions and the displacement has unpredictable magnitude. Finaly, the motion of the system will be the single periodic harmonic response again when the non-dimensional speed is bigger than 3.2.
Fig. 3Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.05)
When the damping ratios are at , the bifurcation diagram of the system with the non-dimensional speed is shown in Fig. 4. Comparing it with Fig. 3, the bifurcation characteristics is more obvious and the chaotic region is smaller. The bifurcation diagram of the system is shown in Fig. 5 when the damping ratios are at . Fig. 5 shows that the motion of the system is only single periodic response when the damping ratios are bigger enough. So the chaos can be avoided by increasing the damping ratios.
Fig. 4Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.1)
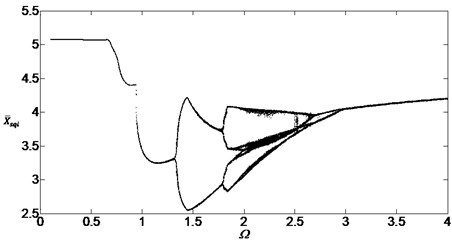
Fig. 5Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.2)
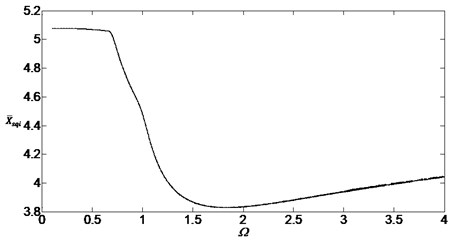
Figs. 6, 7 and 8 are the bifurcation diagrams when the damping ratios are at 0.05, 0.1 and 0.2. They show the bifurcation characteristics of the system with the non-dimensional speed between inside planetary gears and outside planetary gears.
When the damping ratios are smaller such as 0.05 or 0.1, the dynamic behavior of the system is found to be a periodic motion, then the system will pass through the chaotic regions and the single periodic regions. When the damping ratios are bigger such as 0.2, the dynamic behavior is found to be the single periodic harmonic response and the vibration form will not change with the speed change. Similarly, comparing with the Figs. 3, 4 and 5, the damping ratios will still influence the bifurcation characteristics greatly.
Fig. 6Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.05)
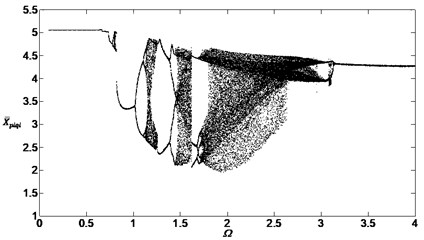
Fig. 7Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.1)
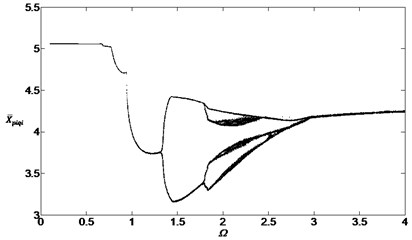
Fig. 8Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.2)
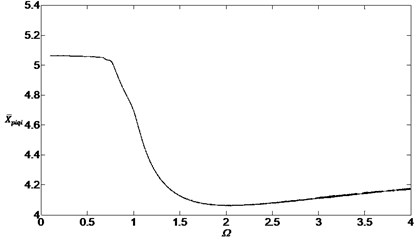
In order to investigate the influence of the gear backlashes on the bifurcation characteristics, Fig. 9 shows the results of the numerical simulation between the sun gear and the inside planetary gears when , . Comparing Fig. 9 with Fig. 4, it can be found that the shape of the bifurcation diagram don’t change but the dimensionless displacements reduce whatever the dimensionless speed will be set. So the displacement amplitude can be reduced through reducing the gear backlashes. But the method can’t avoid the chaos.
Similarly, the influence of the gear backlashes on the bifurcation characteristics of the dimensionless displacement has same rule as Fig. 9 between inside planetary gears and outside planetary gears. Fig. 10 shows the results of the numerical simulation between inside gear and the outside planetary gears when , Comparing Fig. 10 with Fig. 7, it can be found that the shape of the bifurcation diagram didn’t change but the dimensionless displacements reduced. So the displacement amplitude can be reduced through reducing the gear backlashes. However, the method can’t avoid the chaos too.
Fig. 9Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.1, bsqi=bpiqi=30 μm)
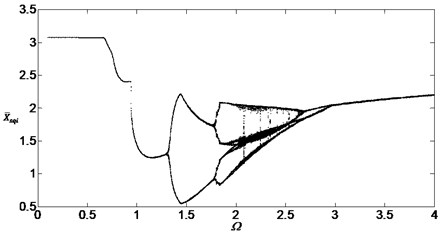
Fig. 10Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.1, bsqi=bpiqi=30 μm)
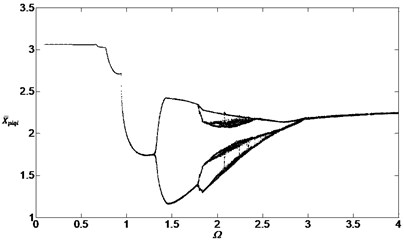
The bifurcation diagram of the dimensionless displacement between the sun gear and the inside planetary gear is shown as Fig. 11 when , . Comparing Fig. 11 with Fig. 4, the displacement amplitude didn’t change but the bifurcation diagram shifted left for a distance, that is to say, the smaller dimensionless speed can cause bifurcation and chaos when the meshing errors are increased.
Fig. 11Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.1, Esqi=Epiqi=20 μm)
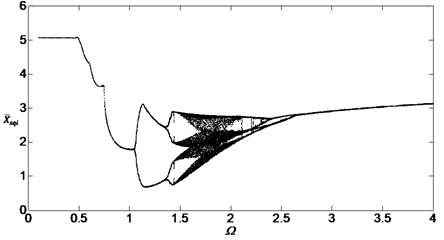
Similarly, the influence of the meshing errors on the bifurcation characteristics of the dimensionless displacement in Fig. 12 has the same rule as Fig. 11 between inside planetary gears and outside planetary gears. Fig. 12 shows the results of the numerical simulation between inside gear and the outside planetary gears when , Comparing Fig. 12 with Fig. 7, it can be found that the shape and the dimensionless displacement of the bifurcation diagram didn’t change, but the diagram translated left for a distance too. The smaller dimensionless speed can cause bifurcation and chaos when the meshing errors are increased, meanwhile, the method can’t avoid the chaos too.
Fig. 12Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.1, Esqi=Epiqi=20 μm)
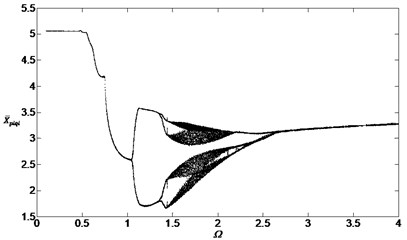
Finally, we investigated the bifurcation characteristics of the vibration system with external noises, that is to say, the parameters can be set at and in Eq. (14). The bifurcation is shown in Fig. 13.
Comparing Fig. 13 with Fig. 4, the external noises changed the chaotic regions and the vibration system would be influenced by its own characteristics and the external noise. Fig. 14 and Fig. 15 are obtained after changing the parameters , and . These bifurcation diagrams show that the external noise will influence the vibration system obviously when the amplitudes and smaller value of will cause more obviously local vibration superposition but not obviously when .
Fig. 13Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.1, Esqi=Epiqi=10 μm, B1=B2=100 Nm, Λ=0.1)
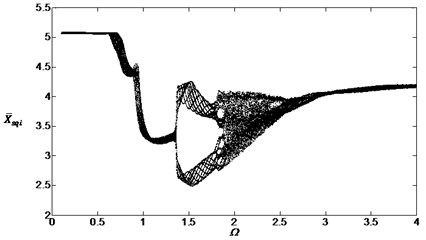
Fig. 14Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.1, Esqi=Epiqi=10 μm, B1=B2=100 Nm, Λ=2)
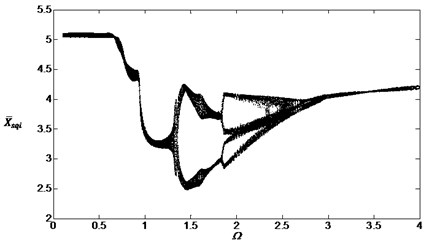
Fig. 15Bifurcation diagram of the system with non-dimensional planetary speed Ω (ξ1=ξ2=0.1, Esqi=Epiqi=10 μm, a) B1=B2=100 Nm, Λ=40; b) B1=B2=10 Nm, Λ=0.1; c) B1=B2=10 Nm, Λ=2; d) B1=B2=10 Nm, Λ=40)
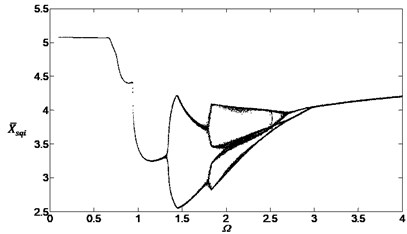
a)
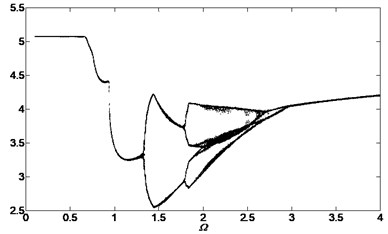
b)
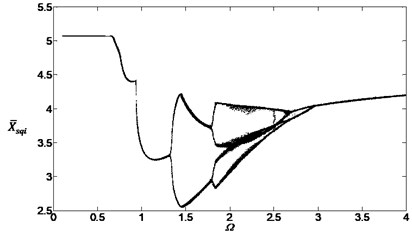
c)
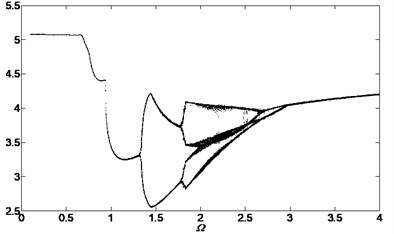
d)
4. Conclusions
This paper investigated the planetary gear processing device and established a nonlinear dynamic model. The model considered errors of transmission, time varying meshing stiffness and gear backlashes, what’s more, the solution of the dimensionless equations of the system was carried out by using the method of numerical integration. According to different bifurcation diagrams, the vibration properties of the planetary gear system were investigated and three influencing factors were researched.
(1) The planetary gear train processing device with translational motion has abundant bifurcation characteristics because of the nonlinear factors. The results reveal that the motion state of the system will change from periodic motion to chaos, then the system will return to the periodic motion as the dimensionless speed increases.
(2) The bifurcation characteristics of the system will influenced greatly by the damping ratios and it can avoid the chaos by the way of increasing the damping ratios. So the fatigue failure in the processing device can still be avoided.
(3) Reducing the gear backlashes can reduce the dimensionless displacement amplitude. So it is very important to control the gear backlashes.
(4) Increasing the meshing errors can make the bifurcation diagrams shift left for a distance but this way can not avoid the chaos and reduce the displacement amplitude.
(5) The external noise can influence bifurcation characteristics of the system and it can change the chaotic regions with the changes of amplitude and angle velocity of load torque.
References
-
Zaigang Chen, Yimin Shao Dynamic simulation of planetary gear with tooth root crack in ring gear. Engineering Failure Analysis, Vol. 31, 2013, p. 8-18.
-
Song Aiping, Wu Weiwei, Gao Shang, Gao Wenjie The ideal geometry parameters of arch cylindrical gear and its process method. Journal of Shanghai Jiaotong University, Vol. 12, Issue 44, 2010, p. 1735-1740.
-
Cunliffe F., Smith J. D., Welbourn D. B. Dynamic tooth loads in epicyclic gears. Journal of Manufacturing Science and Engineering, Vol. 95, Issue 2, 1974, p. 578-584.
-
A. Kahraman Natural modes of planetary gear trains. Journal of Sound and Vibration, Vol. 173, Issue 1, 1994, p. 125-130.
-
A. Kahraman Free torsional vibration characteristics of compound planetary gear sets. Mechanism and Machine Theory, Vol. 36, Issue 8, 2001, p. 953-971.
-
Sheng Li, Qingming Wu, Zhiqiang Zhang Bifurcation and chaos analysis of multistage planetary gear train. Nonlinear Dynamics, Vol. 75, Issue 1-2, 2014, p. 217-233.
-
J. Lin, R. G. Parker Sensitivity of planetary gear natural frequencies and vibration modes to model parameters. Journal of Sound and Vibration, Vol. 228, Issue 1, 1999, p. 109-128.
-
J. Lin, R. G. Parker Analytical characterization of the unique properties of planetary gear free vibration. Journal of Vibration and Acoustics, Vol. 121, Issue 3, 1999, p. 316-321.
-
Blankenship G. W., Kahraman A. Steady state forced response of a mechanical oscillator with combined parametric excitation and clearance type nonlinearity. Journal of Sound and Vibration, Vol. 185, Issue 5, 1995, p. 743-765.
-
P. Velex, L. Flamand. Dynamic response of planetary trains to mesh parametric excitations. Journal of Mechanical Design, Vol. 118, Issue 1, 1996, p. 7-14.
-
A. Kahraman G. W. Blankenship. Experiments on nonlinear dynamic behavior of an oscillator with clearance and periodically time-varying parameters. Journal of Applied Mechanics, Vol. 64, Issue 1, 1997, p. 217-226.
-
J. Lin, R. G. Parker Planetary gear parametric instability caused by mesh stiffness variation. Journal of Sound and Vibration, Vol. 249, Issue 1, 2002, p. 129-145.
-
J. Lin, R. G. Parker Structured vibration characteristics of planetary gears with unequally spaced planets. Journal of Sound and Vibration, Vol. 233, Issue 5, 2000, p. 921-928.
-
R. G. Parker A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration. Journal of Sound and Vibration, Vol. 236, Issue 4, 2000, p. 561-573.
-
R. G. Parker, Xionghua Wu. Vibration modes of planetary gears with unequally spaced planets and an elastic ring gear. Journal of Sound and Vibration, Vol. 329, 2010, p. 2265-2275.
-
Sun Zhimin, Ji Linhong, Sheng Yunwen Nonlinear dynamics of 2K-H planetary gear train. Journal of Tsinghua University, Vol. 43, Issue 5, 2003, p. 636-639.
-
Li Tongjie, Zhu Rupeng, et al. Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear train. Journal of Mechanical Engineering, Vol. 47, Issue 21, 2011, p. 76-83.
-
Chang-Jian C. W., Chen C. K. Chaos and bifurcation of a flexible rub-impact rotor supported by oil film bearings with non-linear suspension. Mechanism and Machine Theory, Vol. 42, Issue 3, 2007, p. 312-333.
-
Chang-Jian C. W., Chen C. K. Bifurcation and chaos analysis of a flexible rotor supported by turbulent long journal bearings. Chaos Solitons Fractals, Vol. 34, Issue 4, 2007, p. 1160-1179.
-
Fakher Chaari, Tahar Fakhfakh, Riadh Hbaieb, et al. Influence of manufacturing errors on the dynamical behavior of planetary gear. The International Journal of Advanced Manufacturing Technology, Vol. 27, Issue 7-8, 2006, p. 738-746.
-
Z. G. Chen, Y. M. Shao, T. C. Lim Non-linear dynamic simulation of gear response under the idling condition. International Journal of Automotive Technology, Vol. 13, Issue 4, 2012, p. 541-552.
-
Sun Zhijun, Hou Li, Wei Yongqiao, et al. A translation processing device of Circular-Arc-Tooth- Trace cylindrical gear. CN 103203647 A, China, 2013.
-
Li Runfang, Wang Jiangjun Dynamics of gear system: Vibration, shock and noise. Science Press, Beijing, 1997.
About this article
This paper was supported by National Natural Science Foundation of China (Grant No. 51375320). The authors would like to acknowledge the financial support.
