Abstract
The effect of a woodpecker’s head structure on shock isolation was investigated from a dynamic point of view. A simplified multi-degree-of-freedom model was set up to study shock isolation characteristics of a woodpecker’s head. The shock-isolation performance of this model was calculated and analyzed by changing the dynamic parameters. And it was evaluated by two indexes: the absolute acceleration of the skull bone and the relative displacement between the skull bone and the beak. A bionic helmet model subjoining the elastic damping layer and the cushion pad was presented. Calculating the three-dimensional shock response surfaces validated it.
1. Introduction
A woodpecker is known to peck the hard wood surface of a tree at a rate of 18 to 22 times per second with a deceleration of 1200 g, yet with no sign of a blackout or brain damage [1]. These facts aroused the interest of many researchers. Schwab [2] compared the structure a woodpecker’s head with the structure of a human head. He argued that the reasons why a woodpecker avoids headaches when dumping the wood, is that the special construction of its head is protecting the woodpecker: a thick bony skull with a relatively spongy bone, a small subarachnoid space with almost no cerebrospinal fluid, a small ratio of brain weight to brain surface, and so on. Gibson’s [3] study recognized three key reasons: a small size of the head, the short duration of the impact, and the orientation of the brain within the skull.
To further research the effects of a woodpecker’s head structure regarding the protection of the brain, Oda et al. [4] analyzed the shock stress in a woodpecker’s head with the Finite Element Model (FEM). Wang et al. [5] investigated the role and the structures of the beak and the cranial bone in avoiding impact injury of a woodpecker’s head with FEM.
The structure of a woodpecker has been applied in the field of engineering. Li and Zhang [6] developed a vibration isolation platform based on a woodpecker bionics mechanics. Yoon and Park [1] presented a woodpecker’s head with a mass-spring-damping model and designed a bio-inspired shock-absorbing system. Vincent et al. [7] modeled a woodpecker with a low-inertia hammer.
This paper studies the effect that a woodpecker’s head structure has on shock isolation. The study is done from a dynamic point of view by simplifying a woodpecker’s head into a multiple-degree-of-freedom system. Based on the analysis of shock isolation characteristics, a bionic helmet is proposed. Two main performance indexes of the bionic helmet are discussed: the maximum absolute acceleration and the relative displacement [8, 9]. The former index represents the maximum force on the object; and the latter represents the necessary space to buffer the shock.
2. Modeling the woodpecker’s head
A woodpecker pecks a tree at an amazing speed of about 20 beats per second and a deceleration of 1200 g without brain damage. Researchers [1, 2, 4] outline to following factors as main reasons:
a) The beak of a woodpecker is vertically large and flat. The beak consists of an upper beak and a lower beak. The lower beak is straightly extended to the neck, as shown in Fig. 1. It is considered that these characteristics allow the stress wave, which is generated at the tip of the beak, to straightly escape behind the brain.
b) A woodpecker has an extended part of a tongue called the hyoid bone. It goes from the jaws to the back portion of the skull, as shown in Fig. 1. The hyoid bone acts as a buffer and retards the shock into the skull bone.
c) The bone in the front of the skull bone is porous. It helps disperse the shock propagating to the brain. The little space between the brain and the skull contains some cerebral fluid, which can isolate shock force.
Fig. 1The head construction of a woodpecker
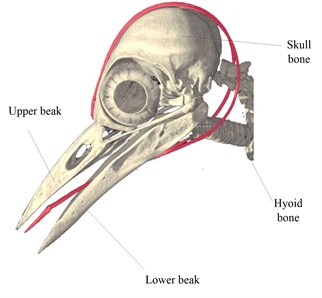
In this study, a simplified mass-damper-spring lumped parameter model for a woodpecker’s head is prepared with the following assumptions: (a) By considering a tree as flexible foundation, it is treated as a vibration reducing layer, which reduces shock excitation transmitted into a woodpecker; (b) the shock energy when a woodpecker drums a tree is divided into two parts: one part transmits into the skull bone from the upper beak and hyoid bone; the other one transmits into the body from the lower beak; (c) In order to analyze the problems of shock isolation characteristics easily, the stiffness and damping of the hyoid bone and the upper beak are treated as coupled. This is because the mass of the hyoid bone is rather negligible compared with the beak; (d) The skull bone and its accessories are treated as an entirety since the damping mechanism in the skull bone is too complex to be clearly represented.
Based on the above analysis, a head shock absorption model is established and shown in Fig. 2, and the dimensional parameters are shown in Table 1.
Fig. 2The simple mass-spring-damper model of the head of a woodpecker
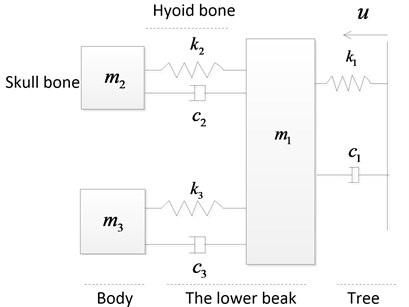
Table 1Parameters of the woodpecker isolation system used in the analysis
Structure | Parameter | Symbol | Value | Source of data |
Tree | Stiffness | 1000 N/m | JR Moore and DA Maguire [10] | |
Damping coefficient | 10 N·s/m | |||
Beak | Mass | 2.1×10-3 N·s/m | Sang-Hee Yoon and Sungmin Park [1] | |
Stiffness | 6.67×104 N/m | |||
Damping coefficient | 0.37 N·s/m | |||
Hyoid bone | Stiffness | – | ||
Damping coefficient | 5.63 N·s/m | |||
Skull bone | Mass | 6.4×10-3 kg | ||
Body | Mass | 6×10-2 kg | JFV Vincent et al. [7] |
The motion equations of the simple mass-spring-damper model can be express as:
where , and , respectively, indicate the masses of the beak, the skull bone and the body;, and represent the damping coefficients of the tree, the hyoid bone and the lower beak; , and are the stiffness coefficients of the tree, the hyoid bone and the beak; , and are the absolute displacements of the beak, the skull bone, and the body, and the dots denote derivatives with respect to time ; is the absolute displacement of the tree, and its second derivative to time represents the shock excitation acting on the beak. The shock excitation is assumed to be a half-sine pulse:
where and denote the amplitude and the duration of the impact, respectively.
3. Shock isolation characteristics of a woodpecker’s head
The shock vibration suppression is influenced by two performance indexes: the maximum responses of the absolute acceleration and the relative displacement [8, 9]. The former characterizes the maximum force that the object sustains. The latter characterizes the maximum displacement of the object relatively to the other parts of the system. When the maximum force exceeds limitation that the object could endure, the object will be damaged. And if the maximum relative displacement exceeds the space of the parts, the parts will crash with each other.
In this section, the shock isolation performance of the woodpecker’s head mass-spring-damper model is evaluated by using the Runge-Kutta method. The initial conditions on are set to zero, i.e., at . The shock excitation during , in Eq. (2), is assumed to be 0.02 s. Based on the results, the effect of the woodpecker isolation system on shock acceleration and displacement response of the skull bone is studied.
Fig. 3 shows the acceleration response and relative displacement responses of the skull bone with different values of the stiffness of the tree . It can be seen that a smaller value of may be in favor of reducing the responses of the skull bone, i.e. the absolute acceleration and the relative displacement to the beak. As shown in Fig. 3(a), the maximum absolute acceleration is nearly equal to the shock excitation amplitude when the value of 100000 N/m. This means that the shock isolation system is invalid as the ratio drops to 0.18 % due to the reduction of . In Fig. 3(b), the relative displacement has the same trend as the absolute acceleration. This means that the oscillation amplitude of the woodpecker’s head will reduce if it drums a soft tree. Assumed that a woodpecker pecks a hard surface, for example, a steel plate, its head would suffer huge shock.
Fig. 3Time responses of the skull bone as a function of a tree’s stiffness k1 for a) absolute acceleration, b) relative displacement to the beak
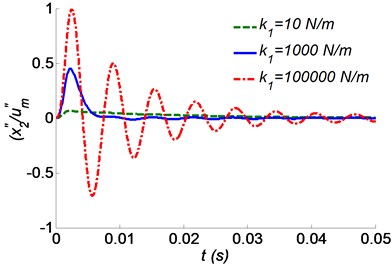
a)
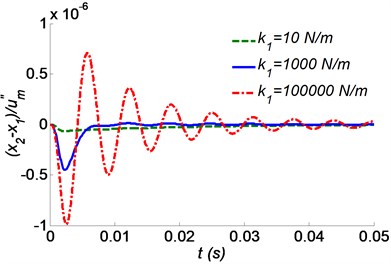
b)
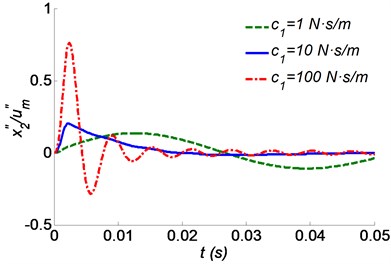
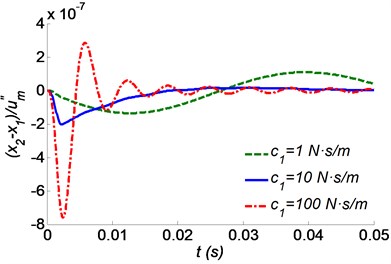
Fig. 4 depicts the influences of the tree’s damping coefficient on the shock response of the skull bone. The peak values of both the acceleration and the displacement curves (when 100 N·s/m) are far greater than those of the other curves. It is obtained that an excessive tree damping may be harmful to a woodpecker. As shown in Fig. 4, the peak amplitudes of both acceleration and displacement are much the same under the cases of 1 N·s/m and 10 N·s/m. This means that the isolation effect is similar to the damping coefficient by less than a limitation value, such as 10 N·s/m. However, with low tree damping, the residual vibration after the shock pulse, will last for a long time. Take the curves 1 N·s/m in Fig. 4 (a) and (b) for example, the skull bone oscillation amplitude would decrease slowly because of low tree damping.
Fig. 4Time responses of a skull bone as a function of the tree’s damping coefficient c1 for a) absolute acceleration, b) relative displacement to the beak
a)
b)
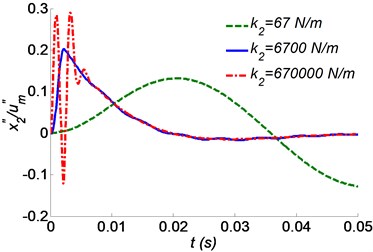
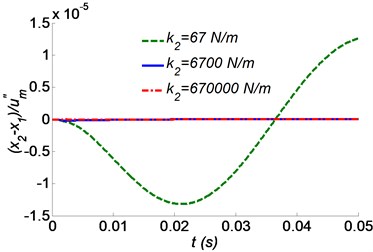
Fig. 5 shows the absolute acceleration and the relative displacement responses with different values of the hyoid bone’s stiffness (the stiffness of the hyoid bone). Fig. 5(a) reveals that the maximum acceleration response increases as the stiffness of the hyoid bone increases. It should be pointed out that the maximum acceleration is not sensitive to the stiffness of the hyoid bone. The maximum acceleration response decreases from 0.3 to 0.15 when the value of decreases from 670000 N/m to 67 N/m. The relative displacement presents the opposite characteristic to the acceleration. This means that a soft stiffness of the hyoid is harmful for the relative displacement control. However, the residual vibration will last for some time with rather small hyoid bone stiffness, as shown in Fig. 5.
Fig. 5Time responses of the skull bone as a function of the hyoid bone’s stiffness k2 for a) absolute acceleration, b) relative displacement to the beak
a)
b)
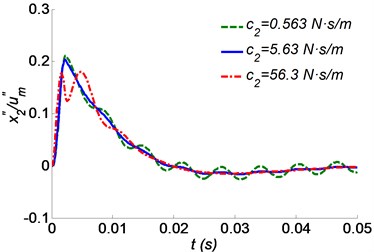
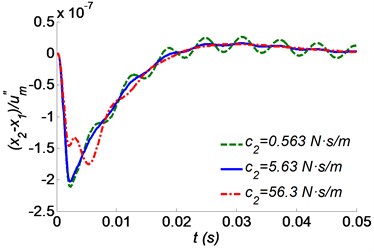
Fig. 6 shows the effects of the hyoid bone damping on shock isolation. It can be seen that the influences of the hyoid bone’s damping on shock responses are not obvious, as shown in Fig. 6. However, a low damping of the hyoid bone is harmful to the control of the residual vibration, as the curve 0.563 N·s/m in the Fig. 6.
Fig. 6Time responses of the skull bone as a function of the hyoid bone’s damping coefficient c2 for a) absolute acceleration, b) relative displacement to the beak
a)
b)
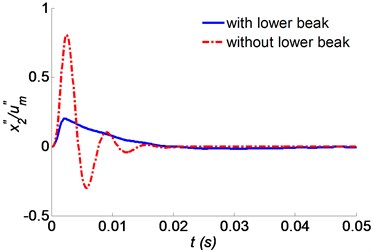
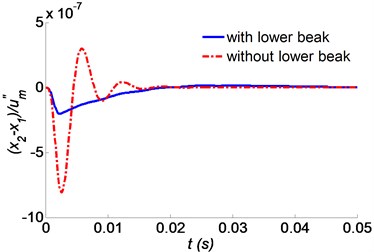
Fig. 7Time responses of the skull bone with or without a lower beak for a) absolute acceleration, b) relative displacement to the beak
a)
b)
The former FEM study [5] shows that if the upper beak is about 1.2 mm shorter than the lower beak, the pecking force transmitted into the brain will greatly decrease. In order to evaluate the effect that the lower beak has on shock response, the absolute acceleration and relative displacement responses of the skull bone are calculated by comparing woodpeckers with and without the lower beak. Fig. 7 shows that the lower beak plays an important role in reducing the shock transmitted into the skull bone. The maximum absolute acceleration and the relative displacement would increase about 4 times if the woodpecker would have no lower beak. It can be explained that, the shock energy transmitted into the skull bone is shunted into the body by the lower beak.
In general, the unique head structure enables a woodpecker to bear the shock excitation when it pecks a tree. The lower beak can transmit shock energy into other parts of the body. Additionally, the hyoid bone acts as a cushion and suppresses the oscillation of the skull bone. Moreover, the tree with small stiffness and appropriate damping can effectively reduce the maximum absolute acceleration and the relative displacement of the skull bone.
4. A bionic helmet design based on the shock isolation characteristics of a woodpecker’s head
In the above discussion, the shock isolation performance of a woodpecker’s head is studied. The mechanism of avoiding brain damage can be described as the lower beak transmitting the energy into other parts of the body, the hyoid bone buffering the shock, and the soft tree decreasing the impact force. In this section, a bionic helmet based on analysis of the isolation characteristics of a woodpecker’s head is discussed.
Compared to a common helmet, the surface of the bionic helmet is connected by an elastic damping layer. The bottom of the helmet has a cushion pad, which creates a contact with shoulders, as shown in Fig. 8(a). The elastic damping layer attached to the helmet can retard the impact force when a falling object impacts the helmet, which simulates the effects of a tree in the isolation system of a woodpecker. Additionally, the cushion pad (acting as the lower beak) can transmit the impact force into shoulders.
Fig. 8a) Sketch of a head with a bionic helmet, b) Mass-spring-damper model of the head with a bionic helmet
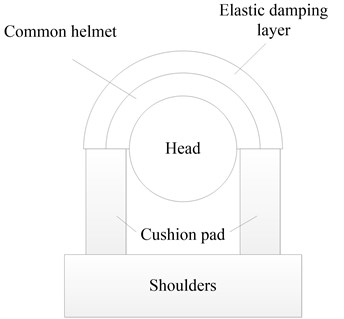
a)
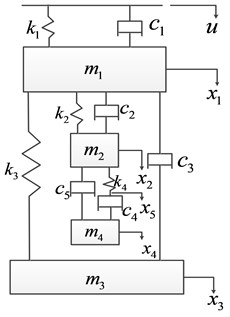
b)
The lumped mass-spring-damping model of the bionic helmet is depicted as Fig. 8(b). The common helmet is idealized as mass , the stiffness coefficient and the damping coefficient . The elastic damping layer is described as the stiffness coefficient and the damping ratio . The cushion pad is described as the stiffness coefficient and the damping ratio , which is connected with shoulders and is described as mass . The head model of a human is simplified as the skull bone connecting with the brain , the stiffness coefficient and the damping coefficient model the mechanical properties of the skull bone, whereas the damper with the damping coefficient characterizers primarily the dissipative properties of the brain. D. V. Balandin et al. used such kind of a human head model with a helmet for limiting performance analysis [11]. Moreover, , , , , and represent, respectively, the displacement of the common helmet, the skull bone, shoulders, the brain, the spring point attachment of to the damping and the elastic damping layer.
The motion equation of the helmet, which is struck by a falling object, can be written as Eq. (3):
The shock excitation is assumed to be a half-sine pulse described as:
where and denote the amplitude and the duration of the impact, respectively.
The model parameters used in the numerical calculation are shown in Table 2. The head parameters are determined according the study of Balandin, Boloynik and Pilkey [11]. The parameters of the elastic damping layer and the cushion pad are considered as variables in the numerical calculation, and their effects on the shock isolation will be evaluated.
Table 2Parameters of the bionic helmet isolation system used in the analysis
Structure | Parameter | Symbol | Value |
Elastic damping layer | Stiffness | – | |
Damping coefficient | – | ||
Common helmet | Mass | 0.425 kg | |
Stiffness | 1×105 N/m | ||
Damping coefficient | 10 N·s/m | ||
Skull bone | Mass | 0.45 kg | |
Stiffness | 1.35×107 N/m | ||
Damping coefficient | 1.7×104 N·s/m | ||
Shoulders | Mass | 20 kg | |
Cushion pad | Stiffness | – | |
Damping coefficient | – | ||
Brain | Mass | 4.09 kg | |
Damping coefficient | 157.6 N·s/m | ||
Shock excitation | duration | 0.002 s |
According to Eq. (3) and Eq. (4), three-dimensional shock responses of a head with a bionic helmet are calculated as a function of the elastic damping layer’s stiffness and damping coefficients. The three-dimensional shock responses incorporate not only the maximum responses and the stiffness of the system, but also the damping ratio simultaneously. The projection of the three-dimensional shock response surfaces on the stiffness-response plane is so-called shock response spectrum if transforming the coordinate of stiffness into natural frequency, for the damping ratio and the mass are certain values. The shock response spectrum represents the relationship between the maximum response and the natural frequency of the system, when a known shock excitation acts on the system. It is widely used in the impact analysis [9, 12].
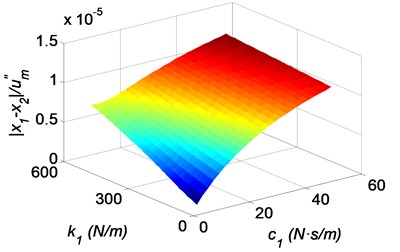
The calculation results are plotted in Fig. 9. It can be seen that the absolute acceleration and the relative displacement to the skull bone of the brain decrease with the decreasing stiffness coefficient and the damping coefficient of the elastic damping layer, as shown in Fig. 9(a) and (b). It means that a soft damping layer is advantageous when decreasing the force and the oscillation amplitude of the brain. Besides, the relative displacement of the skull bone to the helmet indicates the same trends with the brain, as shown in Fig. 9(c). The values of the skull bone’s relative displacement to the helmet are larger than the brain’s to the skull bone. Therefore it should have enough space between the helmet and the head in the design.
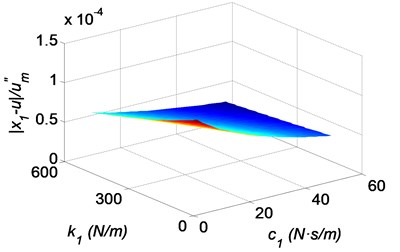
However, if the stiffness coefficient and the damping coefficient are too small, the relative displacement between the elastic damping layer and the helmet will be enlarged, as shown in Fig. 9(d). It means that the layer with a soft material should be thick enough to buffer the shock.
Fig. 9Three-dimensional shock response surfaces of the head with the bionic helmet, as a function of the stiffness coefficient and the damping coefficient of the elastic damping layer: a) absolute acceleration of the brain, b) relative displacement of the brain to the skull bone, c) relative displacement of the skull bone to the helmet, d) relative displacement of the elastic damping layer to the helmet, where k3= 500 N/m, c3= 10 N·s/m
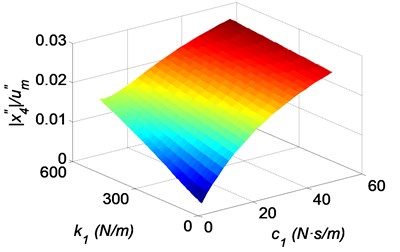
a)
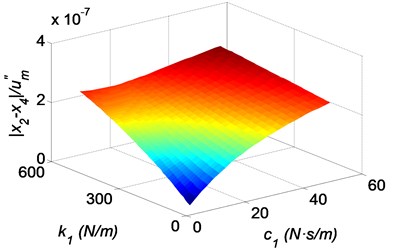
b)
c)
d)
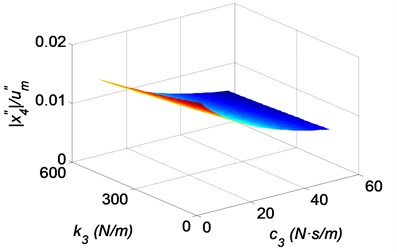
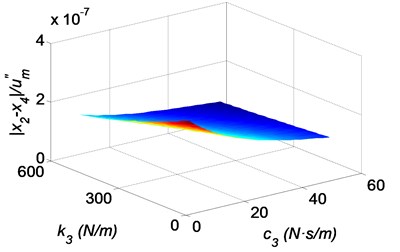
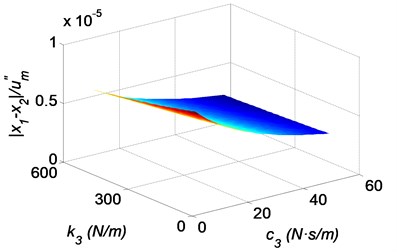
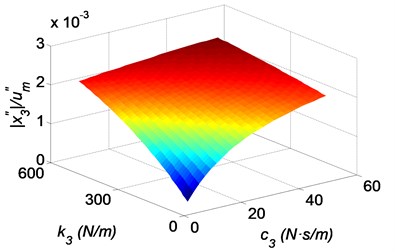
The effects of the cushion pad on the shock responses of the head with the functional bionic helmet are shown in Fig. 10. It is readily seen that large stiffness and the damping of the cushion pad are beneficial when reducing the acceleration of the brain, the relative displacement of the skull bone to the helmet and to the brain, as shown in Fig. 10(a-c). Therefore a harden cushion pad is advantageous to protect the head. However, the acceleration of shoulders increases with the increasing stiffness and the damping of the cushion pad, as shown in Fig. 10(d). The reason is that the shock energy is transmitted into the shoulders from the brain.
In general, the functional bionic helmet presents similar characters on shock isolation as a woodpecker’s head. The soft elastic damping layer representing a tree and the harden cushion pad representing a lower beak could effectively decrease both the force transmitted into the brain and the relative displacement between the brain and the skull bone. However, the elastic damping layer should be thick enough to buff the impact energy, or the falling object may breakdown the lay and impact the helmet directly. The harden cushion pad may product force on shoulders. Therefore it should be comprehensively considered when designing a bionic helmet.
Fig. 10Three-dimensional shock response surfaces of the head with the bionic helmet, as a function of the stiffness coefficient and the damping coefficient of the cushion pad: a) absolute acceleration of the brain, b) relative displacement of the brain to the skull bone, c) relative displacement of the skull bone to the helmet, d) relative displacement of the elastic damping layer to the helmet, where k1= 200 N/m, c1= 10 N·s/m
a)
b)
c)
d)
5. Conclusions
A lumped multi-degree-of-freedom model of a woodpecker’s head was proposed in this paper. Based on this, the effects that the components of a woodpecker head have on shock isolation were analyzed. The discussions show that small stiffness and appropriate damping enables a tree to effectively reduce the shock force; the hyoid bone can further weaken the skull bone oscillation; the lower beak can decentralize the shock energy into the skull bone.
A bionic helmet that subjoins the elastic damping layer and the cushion pad was presented according to the isolation characters of a woodpecker’s head. The three-dimensional shock response surfaces show that proper parameters of the elastic damping layer and the cushion pad can effectively decrease both the force transmitted into the brain and the relative displacement between the brain and the skull bone.
References
-
Yoon S. H., Park S. A mechanical analysis of woodpecker drumming and its application to shock-absorbing systems. Bioinspiration & Biomimetics, Vol. 6, Issue 1, 2011, p. 016003.
-
Schwab I. R. Cure for a headache. British Journal of Ophthalmology, Vol. 86, Issue 8, 2002, p. 843-843.
-
Gibson L. J. Woodpecker pecking: how woodpeckers avoid brain injury. Journal of Zoology, Vol. 270, Issue 3, 2006, p. 462-465.
-
Oda J., Sakamoto J., Sakano K. Mechanical evaluation of the skeletal structure and tissue of the woodpecker and its shock absorbing system. JSME International Journal Series A, Vol. 49, 2006, p. 390-396.
-
Wang L., Cheung J. T. M., Pu F., et al. Why do woodpeckers resist head impact injury: a biomechanical investigation. PloS One, Vol. 6, Issue 10, 2011, p. e26490.
-
Guoping L., Chunliang Z. Active vibration control of an isolation platform based on state space LQG. International Conference on. IEEE, Robotics and Biomimetics, 2005, p. 427-431.
-
Vincent J. F. V., Sahinkaya M. N., O’Shea W. A woodpecker hammer. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 221, Issue 10, 2007, p. 1141-1147.
-
Ibrahim R. A. Recent advances in nonlinear passive vibration isolators. Journal of Sound and Vibration, Vol. 314, Issue 3, 2008, p. 371-452.
-
Harris C. M. Shock and vibration handbook. McGraw-Hill, 1996.
-
Moore J. R., Maguire D. A. Natural sway frequencies and damping ratios of trees: concepts, review and synthesis of previous studies. Trees, Vol. 18, Issue 2, 2004, p. 195-203.
-
Balandin D. V., Bolotnik N. N., Pilkey W. D. Optimal protection from impact. Shock and Vibration, CRC Press, 2001.
-
Wang J., Wang Z. W., Lu L. X.,et al. Three-dimensional shock spectrum of critical component for nonlinear packaging system. Shock and Vibration, Vol. 18, Issue 3, 2011, p. 437-445.
About this article
This work was supported by the National Natural Science Foundation of China (No. 51175195).
