Abstract
This paper focuses on solving a series of problems, in particular, the extraction of planetary gear fault characteristics for cracked and broken teeth, using the frequency domain information exchange method. First, we discuss deficiencies in classical stochastic resonance fault feature extraction method. A number of issues are associated with adaptive stochastic resonance based on the re-scaling frequency method used during the small parameter issues, such as sampling frequency ratio constraints and easily induced aliasing of the target frequency band. Second, to overcome the above-mentioned problems, this paper proposes a frequency domain information exchange optimization method. Simulations were carried out used the proposed method and results were compared to those obtained using previously presented adaptive stochastic resonance based on the re-scaling frequency method. Finally, tests were performed on an experimental planetary gearbox failure platform to further verify the frequency domain information exchange method for effectively extracting planetary gear crack and missing tooth fault features.
Highlights
- The possibility of extracting fault features of broken teeth and planetary gear by frequency domain information exchange method is discussed.
- A frequency-domain information exchange optimization method is proposed through theoretical analysis.
- Experiments show that the frequency domain information exchange method can effectively extract the characteristics of planetary gear cracks and tooth missing faults.
1. Introduction
Planetary gearbox faults cause changes in the position of gears and sensors during operation resulting in signal modulation. These dynamic fault signals can be acquired by sensors, however, the complex transmission path results in attenuation. Therefore, the dynamic responses of planetary gearbox systems are very weak. Moreover, planetary gears usually work under low-speeds and heavy-loading conditions, in addition to harsh working environments that can lead to serious Gaussian random noise in the vibration response signals. Therefore, it is difficult to extract the fault characteristics of planetary gearboxes, in particular, faint features such as the weak signals indicating the early stages of a gear faults. This makes early fault diagnosis extremely difficult [1]. Current feature extraction methods for weak signals are mostly based on Gaussian random noise reduction or suppression, including wavelet analysis [2], singular value decomposition [3],empirical mode decomposition [4], high-order statistical analysis [5], back propagation (BP) neural networks [6], support vector machines [7-9], empirical mode decomposition (EMD) [10, 11], and similar Gaussian random noise reduction methods. The methods mentioned above have excellent outcomes in extracting features from weak signals and mechanical fault diagnosis in some situations. However, weak signals with high Gaussian random noise contamination are only further weakened by attempting to suppress the Gaussian random noise. This can have a considerable impact on feature extraction and make the detection of features in weak signals near impossible.
The stochastic resonance (SR) method uses part of the Gaussian random noise energy to enhance the signal energy [12]. In contrast to current methods, the SR method uses the unwanted Gaussian random noise to enhance weak signal characteristics. Synergetic effects of the nonlinear system, signal, and Gaussian random noise can make SR detection highly effective. Therefore, in recent years, SR has been researched in-depth and applied for weak signal feature extraction and mechanical fault diagnosis. Li et al. [13] studied the SR method and was able to detect impact signals in order to diagnose fixed axis gear faults. Han et al. [14] combined SR with a wavelet transform and successfully detected weak multi-frequency signals. Furthermore, a full-wave-enhanced SR method was proposed by Lu et al. [15] and applied to diagnose faults in rotating machines. Ren et al. [16] demonstrated good classification performance by applying SR to preprocess vibration signals and extract the feature sets. Li et al. [17] applied the Woods-Saxon and Gaussian SR to enhance the characteristic frequency of compressor blades, and effectively extracted early failure characteristics of cracks in the blades. Furthermore, Li et al. [18] studied an SR method based on adaptive singular value decomposition and effectively extracted the fault characteristics of bearings despite the presence of high noise levels.
Nonetheless, a number of problems still need to be solved in order to effectively use existing SR methods for planetary gear fault diagnosis. One of the main issues is that to achieve optimal effects, the SR parameters must first be optimized to obtain an SR system that best matches the input signal. In addition, to effectively process real signals, it is necessary to overcome the small-parameter limits required to satisfy the adiabatic approximation of SR. Moreover, an improved SR method better suited to the complex spectra and rich harmonic components of planetary gearboxes is needed. To address these issues, a method based on frequency information exchange and adaptive SR (FIE-ASR) is proposed and used for planetary gear fault signal processing and feature extraction. The effectiveness of the proposed method was evaluated by applying it to test signals representing planetary gear faults, including a cracked gear tooth and a gear with a missing tooth. Compared to existing methods, such as adaptive SR based on re-scaling frequency (RF-ASR), the proposed method was shown to be more effective in planetary gearbox fault diagnosis.
2. Adaptive stochastic resonance
2.1. Stochastic resonance principle
The SR system can be described by three components: a nonlinear system, Gaussian random noise, and periodic signal. When the synergistic effects of all the three components are optimal, the signal can be clearly enhanced by SR. In this paper, the bi-stable SR system is analyzed. The Langevin equation can be written as:
where and are the bi-stable system parameters, is a periodic input signal, is the amplitude of the input signal, is the characteristic frequency of the signal, is Gaussian white Gaussian random noise, 0, , and is the Gaussian random noise intensity. The potential function of the bi-stable system is usually expressed as:
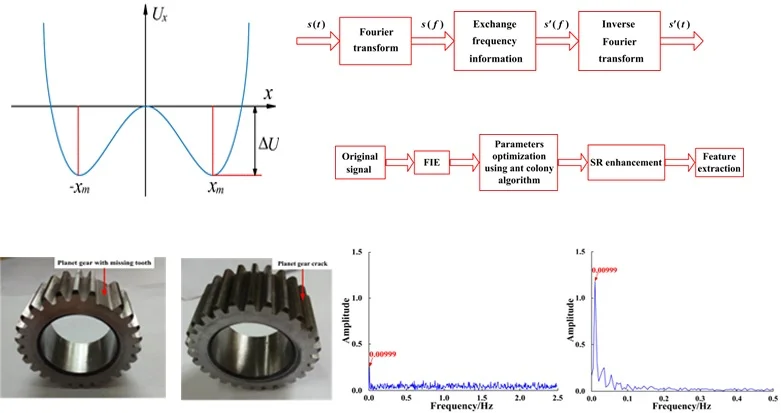
An illustration of the potential well concept is shown in Fig. 1. The bi-stable function has an unsteady state 0 two steady-states , and barrier height . When the input signal is zero, the system is in the steady state. Moreover, when the input signal is weak, sufficient energy does not exist to overcome the barrier, therefore the signal can only move within a single potential well. However, when a certain intensity of Gaussian random noise is added to the weak input signal, a portion of the additional Gaussian random noise energy is transferred to the signal and the signal can overcome the barrier. Thus, a transition between the two steady states occurs, that is, an SR phenomenon occurs.
Fig. 1Potential function of bi-stable SR system
2.2. Optimization of adaptive stochastic resonance parameters
According to the principles of SR, the potential barrier is an important factor affecting the SR phenomenon. Barrier height can be determined by selecting the values and . Therefore, the choice of system parameters and plays a pivotal role in whether SR occurs. To achieve optimal signal processing with SR method, it is particularly important for the system parameters to be adaptively optimized. In general, SR parameter optimization methods use a single system parameter as the optimization objective while all other parameters remain unchanged. Then, the influence of the parameter on the system output is discussed. However, these parameter optimization methods are local optimization methods that ignore the interaction between various parameters of the SR system. Therefore, only relative optimal values of the SR system parameters can be obtained [19].
In this paper, to obtain the globally optimal solution of the SR system parameters and to achieve the best signal processing effects using the SR method, an adaptive SR method is proposed that simultaneously optimizes parameters and using the ant colony algorithm [20, 21].
2.3. Verification of the adaptive stochastic resonance method
2.3.1. Simulation signal verification
An expression of the input signal can be given as:
where 0.03, 0.05 Hz, and the Gaussian random noise intensity of is 0.25. A sampling frequency 20 Hz is assumed with 2000 sampling points.
First, the traditional parameter optimization method was used to optimize a single parameter of the system. One parameter was fixed, 1, and was optimized. The simulation signal spectrum is presented in Fig. 2. Then the other parameter was fixed, 1, and was optimized. The simulation signal spectrum is shown in Fig. 3. Finally, the proposed ant colony algorithm was applied to adaptively optimize the parameters and simultaneously, and the resulting signal spectrum is illustrated in Fig. 4.
Comparing Fig. 4 with Figs. 2 and 3, it can be seen that the proposed ASR method is capable of extracting the signal characteristics more effectively. Thus, the effectiveness and superiority of the proposed method is verified.
Fig. 2Simulation signal spectrum when parameter a is fixed
Fig. 3Simulation signal spectrum when parameter b is fixed
Fig. 4Signal processed using the proposed adaptive SR method
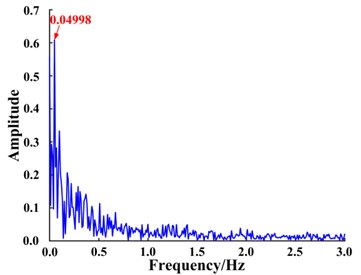
2.3.2. Test signal verification
The adaptive SR method proposed in this paper was applied to process the envelope signal of the fault signal collected from of a planetary gear with a missing tooth. A detailed description of the procedure is provided in Section 4.
As shown in Fig. 5, the fault signal was not successfully extracted as the resulting signal does not contain the fault characteristics. The poor result is owing to the small parameter limits of SR [22, 23]. The method must be improved in order to successfully extract features from signals under real conditions. A detailed description of the adiabatic approximation of small parameters for SR is provided and an improved adaptive SR method is presented that overcomes the small parameter limits, i.e., an adaptive stochastic resonance fault diagnosis method based on frequency information exchange.
Fig. 5Signal processed using the adaptive SR method
3. Fault diagnosis using an adaptive stochastic resonance method based on frequency information exchange
3.1. Small-parameter conditions of SR adiabatic approximation
The function [24] representing the response amplitude of a bi-stable SR system that varies with Gaussian random noise intensity is given by:
however, real engineering signals do not satisfy the small-parameter conditions of the adiabatic approximation, that is, the characteristic frequency of the engineering signal cannot satisfy the condition 1. Therefore, overcoming the limitations of the small-parameter condition of the adiabatic approximation is an urgent problem. If solved, the signal to be processed would be able to undergo the SR phenomenon, thus making it possible to successfully process real engineering signals using the SR method. In this paper, a method based on frequency information exchange (FIE) is proposed to solve the problems associated with the small-parameter conditions of the SR adiabatic approximation. The method is discussed in detail in the next section.
Fig. 6Variation of response amplitude x- of bi-stable SR system with Gaussian random noise intensity D for different characteristic frequencies f0
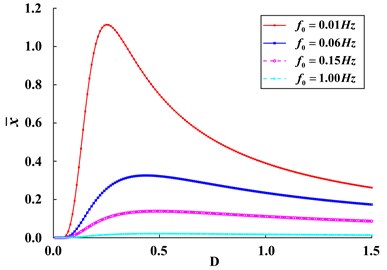
3.2. Mechanism of frequency information exchange
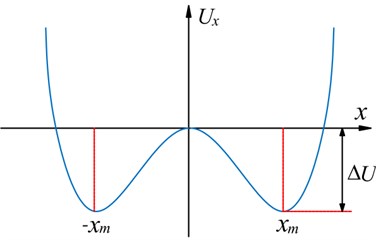
The FIE method involves exchanging frequency information at the characteristic frequency point of the original signal and reference frequency point to obtain a new signal.
A flow chart of the FIE method is presented in Fig. 7. First, the original time domain signal is transformed using the Fourier transform to obtain a frequency domain signal . Then, the frequency information at the characteristic frequency and reference frequency are exchanged. Now, the reference frequency contains the amplitude and phase information at the characteristic frequency . After the frequency domain exchanged, the signal is written as . Finally, the signal can be transformed using the inverse Fourier transform to obtain a new time domain signal .
Fig. 7Flowchart of frequency information exchange (FIE) method

The essence of FIE lies in modulating the upper and lower single sideband signals of the reference frequency signal and characteristic signal, respectively [24]. Letting the reference frequency signal , the characteristic signal , and represent the carrier signal, the reference frequency signal modulated on the upper single sideband is:
Furthermore, the characteristic signal modulated on the lower single sideband is:
where represents the Hilbert transform. Letting , after a single sideband signal modulation the frequency of the reference frequency signal is converted to , the frequency of the characteristic signal is transformed to , and the amplitude and phase information of each signal remain unchanged. That is, frequency information exchange between and occurs.
3.3. Adaptive stochastic resonance method based on frequency information exchange
A flowchart of the FIE-ASR method proposed in this paper is presented in Fig. 8 and the specific steps for implementing the method are as follows:
(1) Process the original signal using the FIE method. This involves exchanging frequency information between the signal characteristic frequency of interest and a reference low frequency. The exchanged signal now meets the small-parameter requirements of the adiabatic approximation.
(2) Optimize the SR system parameters and using the adaptive ant colony algorithm. Use the SNR of the system output signal as the evaluation function of the ant colony algorithm.
(3) Input the transformed signal from Step (2) into the SR system along with the optimized system parameters and from Step (3). The feature signal is now enhanced, and the signal features can be extracted.
Fig. 8Flowchart of the adaptive stochastic resonance method based on frequency information exchange (FIE-ASR)

3.4. Simulation analysis
To verify the effectiveness of the FIE-ASR method, the method was used to process a simulated signal. The input signal can be expressed as:
where 0.25, 1.2 Hz, and the Gaussian random noise intensity of is 0.25. A sampling frequency of 5 Hz was considered with 1000 sampling points. The bi-stable system parameters were 1, 1.
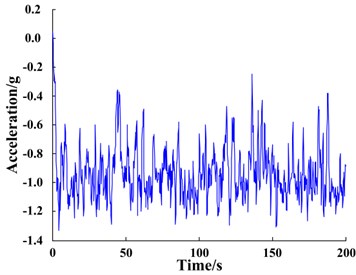
Signal was input into the bi-stable SR system. The time domain waveform of the signal is shown in Fig. 9(a) and the corresponding response is shown in Fig. 9(c). The system is bi-stable; therefore, the input signal does not undergo the SR phenomenon. The input signal spectrum shown in Fig. 9(b) and the response spectrum of the bi-stable system shown in Fig. 9(d), demonstrate that the amplitude at the characteristic frequency of the input signal is not enhanced but instead considerably weakened. The reason for this phenomenon is that the characteristic frequency of the input signal, 1.2 Hz, does not meet the small-parameter conditions required for SR.
Fig. 9Response of bi-stable system based on large-parameter input signal
a) Input signal waveform
b) Input signal spectrum
c) Output signal waveform
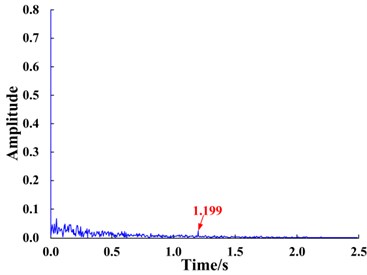
d) Output signal spectrum
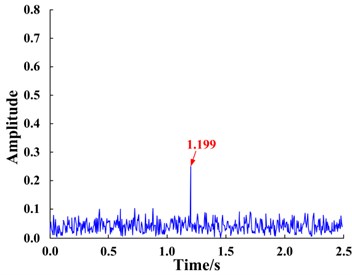
The FIE-ASR method proposed in this paper was used to process the same signal. First, the characteristic frequency information at 1.2 Hz of the input signal was exchanged with the frequency information at the lower reference frequency 0.01 Hz. The transformed signal spectrum is shown in Fig. 11(b). It can be seen that the amplitude and phase information of the reference frequency exist at the characteristic frequency 1.2 Hz, thereby satisfying the small-parameter conditions of SR. The transformed frequency domain signal was subjected to inverse Fourier transformation to obtain the post-FIE time domain signal, as shown in Fig. 11(a). Taking the SNR of the output signal of the bi-stable system as the function to evaluate, the system parameters, and , can be adaptively optimized using the ant colony algorithm. The ranges of initial parameters of the system are 0 < < 10, 0 < < 10 and were each divided into 10 equal parts. For the optimization, the pheromone evaporation coefficient was 0.9, the number of ants was 100, accuracy was set to 0.03, and the maximum number of iterations was 20. Results of the parameter optimization are presented in Fig. 10.
The optimized parameters were input into the bi-stable system and the time domain signals were found to be enhanced after FIE. The response waveform and spectrum of the bi-stable SR system are shown in Fig. 11(c), (d).
The SR phenomenon produced by the system is significant, as seen in Fig. 11(c), (d). Furthermore, the amplitude of the characteristic frequency 0.01 Hz is much larger than (4.7 times) the amplitude of the original signal, thus the original signal is clearly enhanced and amplified, which verifies the effectiveness of the proposed method.
Fig. 10Results of system parameter optimization based on ant colony algorithm
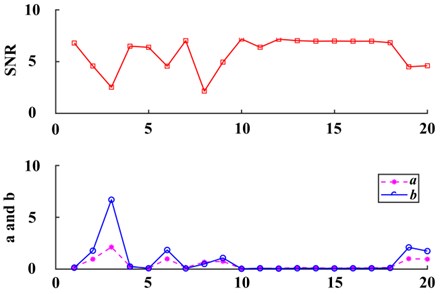
Fig. 11Results of applying the FIE-ASR method to the simulated signal
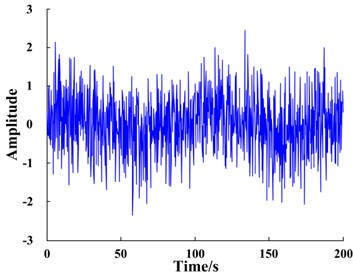
a) Input signal waveform processed by FIE
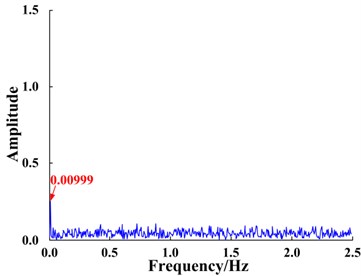
b) Input signal spectrum processed by FIE
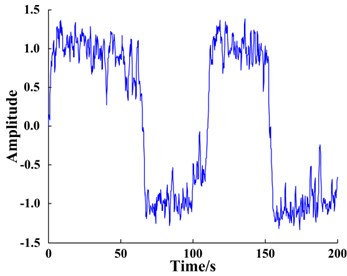
c) Waveform of system response
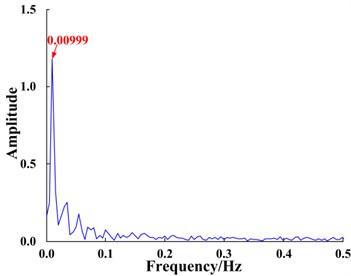
d) Spectrum of system response
4. Experimental validation
4.1. Experimental platform
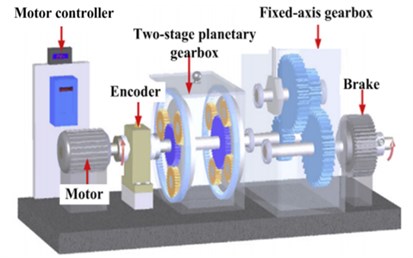
A planetary gearbox fault diagnosis test rig (including experimental systems and three-dimensional models of the experimental systems [21]), as shown in Fig. 12, was used to validate the proposed method.
The planetary gearbox is comprised of a sun gear, three planetary gears, a planetary carrier, and a ring gear. The sun gear is located at the input end and the planet carrier is at the output end. Parameters and characteristic frequencies of the planetary gearbox are presented in Table 1. Various acceleration sensors were arranged on the housing of the gearbox to collect the vibration signals. In this paper, the signal obtained from a sensor fixed to the ring gear located on the front-side of the lower box is analyzed. The sampling frequency of the signal was 51.2 kHz and the sampling time was 200 s. The vibration signals of the planetary gearbox system were collected throughout the experiment under various conditions, including no fault (normal operating conditions), as well as fault conditions such as a cracked planet gear crack or planetary gear with a missing tooth. Photos of the gear faults are shown in Fig. 13. To better simulate real operating conditions, strong noise was artificially introduced into the collected signal data. The time domain waveforms, spectra, and envelope spectra of the original signals are shown in Fig. 14. It can clearly be seen that strong noise disguises the weak signals of the planetary gearbox. In addition, the fault characteristics cannot be isolated regardless of whether the weak signal characteristics are found within the time-domain waveforms, spectra, or envelope spectra; therefore, failure of a planetary gear cannot be predicted without an appropriate signal extraction method.
Fig. 12Planetary gear experimental platform for fault identification

a)
b)
Table 1Configuration parameters and characteristic frequencies of planetary gearbox
Parameter | Value | Parameter | Value |
Number of sun gear teeth | 18 | Meshing frequency / Hz | 216 |
Number of planet gear teeth | 27 | Fault characteristic frequency of planet gear / Hz | 8 |
Number of ring gear teeth | 72 | Fault characteristic frequency of sun gear / Hz | 36 |
Frequency of input / Hz | 15 | Fault characteristic frequency of ring gear / Hz | 9 |
Planet carrier frequency / Hz | 3 | – | – |
Fig. 13Photos of gear fault

a) Cracked planetary gear

b) Planetary gear with a missing tooth
The FIE-ASR method proposed in this paper can be used to process vibration signals, as shown in Fig. 14. Considering the rich spectra and complex sidebands of the response signals of planetary gearbox systems, the envelope spectrum of the original signal under each condition must be analyzed to avoid complex sideband analysis. First, for FIE, the characteristic frequency of the planet gear fault 8 Hz is taken as the target frequency and the reference low frequency is set to 0.004 Hz. To avoid spectrum leakage and the possibility of inaccurate characteristic frequency calculations, frequency information with a bandwidth of 0.05 Hz is exchanged while centered on or . For example, the frequency bandwidth of 8 Hz±0.025 Hz exchanges information with 0.04 Hz±0.025 Hz.
Fig. 14Waveform, spectra, and envelope spectra of original vibration signals under different fault conditions: no fault (normal state), cracked gear, and a gear with a missing tooth
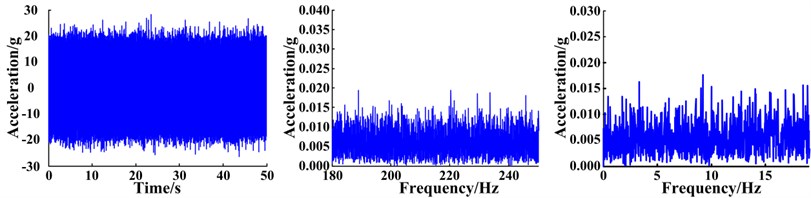
a) Normal state
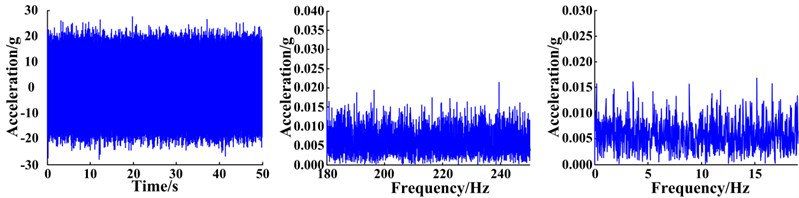
b) Planet gear crack
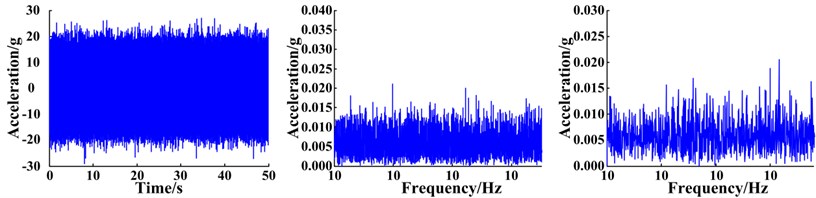
c) Planet gear with a tooth missing
After FIE, the resulting signals were subjected to inverse Fourier transformation to obtain the transformed envelope signal of each fault condition. The adaptive ant colony algorithm was used to optimize the parameters of the bi-stable system and the optimal parameters of each condition were substituted into the system. Then, the transformed envelope signal was input into the system to enhance the SR. The response waveforms and spectra are shown in Fig. 15.
Under normal conditions, no SR phenomenon occurs in the system response, suggesting the signal does not have a characteristic frequency component (Fig. 15). However, the SR phenomenon appears in the response of the systems with a cracked tooth and gear with missing tooth. From the response spectra, the amplitude at the reference frequency of 0.04 Hz is particularly prominent and as the severity of the fault increases, the amplitudes of the signal become more evident. This is reflected by the fact that signals contain the characteristic frequency of the planetary gear fault corresponding to the reference frequency. The results are consistent with the real situation.
Fig. 15Waveforms and spectra of the bi-stable SR system responses for different gear faults based on the FIE-ASR method
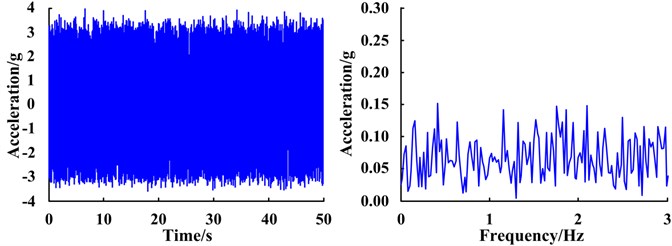
a) Normal state
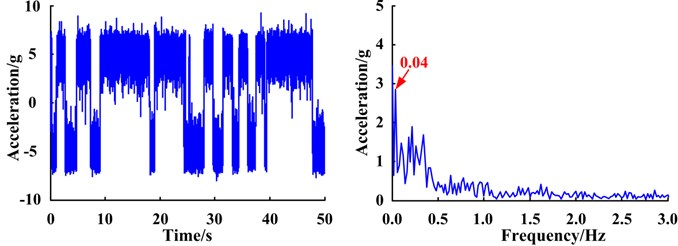
b) Planet gear crack
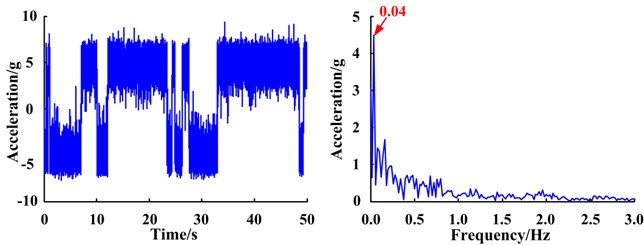
c) Planet gear with a missing tooth
4.2. Comparative analysis
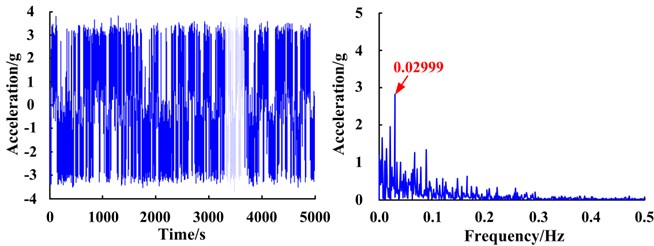
As a comparison, the traditional RF-ASR method was used on the same simulated test signals. Taking the missing tooth planet gear fault as an example, a scale factor 100 Hz was selected, and each characteristic frequency was scaled to 0.003 Hz or 0.08 Hz. The scale-converted envelope signal and envelope spectra are shown in Fig. 16(a). The transformed envelope signal was input into the optimized bi-stable system to obtain the time-domain waveform and spectrum of the system response, as shown in Fig. 16(b).
The signal also undergoes the SR phenomenon (Fig. 16), however, based on the response spectra, it can be seen that the characteristic frequency corresponding to the enhanced frequency point is and not the fault characteristic frequency of the planet gear, and is therefore not the desired result, since it does not indicate whether a gear has failed. This phenomenon is caused by the Lorentz distribution of SR output Gaussian random noise [25]. Since harmonic components of a planetary gearbox are abundant, the characteristic frequency of the planetary carrier is much lower than the planetary gear fault (Table 1). Although the characteristic frequency satisfies the small-parameter conditions of SR after re-scaling the frequency, during the bi-stable SR enhancement process, Gaussian random noise energy converges to low frequencies. As the characteristic frequency decreases, it becomes much easier to enhance. Therefore, after the characteristic frequency of the planetary carrier is enhanced, the system transitions at this frequency, resulting in the SR phenomenon. Since the fault characteristic frequency of the planetary gear has not been enhanced, ultimately it cannot effectively detect planetary gear faults. The FIE-ASR method proposed in this paper overcomes this problem by dealing only with characteristic frequency bands of interest, thereby avoiding the influence of other harmonic components in the system. The above results demonstrate that the proposed method is more suitable than traditional RF-ASR methods for fault feature extraction of planetary gearbox systems with complex spectra.
Fig. 16Signal enhancement using re-scaling frequency-adaptive stochastic resonance (RF-ASR) method
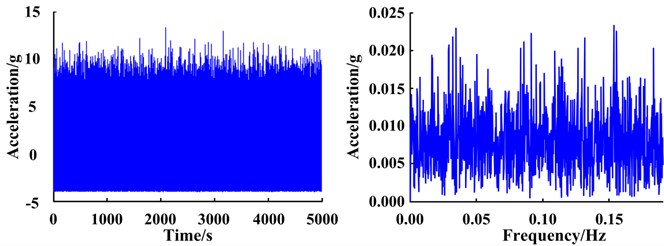
a) Scale-converted envelope signal and envelope spectrum
b) Waveform and spectrum of the system response
5. Conclusions
In this paper, an adaptive SR method based on FIE was studied and applied to fault signal processing and weak feature extraction of planetary gears. Simulated signals were processed and analyzed, and vibration signals of a planetary gear fault diagnosis test rig were processed. Finally, the method was compared to the traditional RF-ASR method. The following conclusions can be drawn:
1) The FIE method overcomes the small-parameter limitations of SR and only considers the frequency bands of interest thereby avoiding the influence of other harmonic components. Moreover, the method solves the problem associated with the complex spectrum structures of planetary gearboxes and rich harmonic components, which previously made feature extraction from weak fault signals difficult.
2) Fault features can be effectively extracted, and the method has been verified via a thorough analysis and by processing the signals of a cracked planetary gear and a gear with a missing tooth.
3) Finally, compared to RF-ASR, the proposed method is more effective in planetary gearbox fault diagnosis.
References
-
Hameed Z., Hon Y. S., Cho Y. M., et al. Condition monitoring and fault detection of wind turbines and related algorithms: a review. Renewable and Sustainable Energy Reviews, Vol. 13, Issue 1, 2009, p. 1-39.
-
Yuan Jing, Wei Ying, Zi Yanyang, et al. Customized multiwavelets by hybrid construction method and applications in fault diagnosis. Journal of Vibration and Shock, Vol. 35, Issue 23, 2016, p. 6-13.
-
Cui Weicheng, Xu Aiqiang, Li Wei, et al. A new method for determining effective order rank of singular value decomposition denoising based on fitting error minima principle. Journal of Vibration and Shock, Vol. 36, Issue 3, 2017, p. 132-137.
-
Liu Haohua, Li Fangyi, Wang Yifan, et al. Gear crack damage localization of the planetary gearbox based on ensemble empirical mode decomposition. Journal of Vibration Measurement and Diagnosis, Vol. 37, Issue 3, 2017, p. 426-431.
-
Zeng Xiaoping, He Yuan, Jian Xin, et al. Adaptive interference cancellation for L-DACS1 by the usage of high order statistics. Acta Electronica Sinica, Vol. 44, Issue 10, 2016, p. 2377-2383.
-
Hao Wang, Feng Zhou Fault diagnosis of wind turbine gearbox based on wavelet packet and back propagation neural network. Noise and Vibration Control, Vol. 35, 2015, p. 154-159.
-
Li Yongbo, Yang Yuantao, Wang Xianzhi, Liua Binbin, Liang Xihui Early fault diagnosis of rolling bearings based on hierarchical symbol dynamic entropy and binary tree support vector machine. Journal of Sound and Vibration, Vol. 428, 2018, p. 72-86.
-
Alireza Zendehboudi, Baseer M. A., Saidur R. Application of support vector machine models for forecasting solar and wind energy resources: a review. Journal of Cleaner Production, Vol. 199, 2018, p. 272-285.
-
Xiao J. Z., Wang H. R., Yang X. C., et al. Multiple faults diagnosis in motion system based on SVM. International Journal of Machine Learning and Cybernetics, Vol. 3, 2012, p. 77-82.
-
Park Sungho, Kim Seokgoo, Choi Joo Ho Gear fault diagnosis using transmission error and ensemble empirical mode decomposition. Mechanical Systems and Signal Processing, Vol. 108, 2018, p. 262-275.
-
Du Yuncheng, Du Dongping Fault detection and diagnosis using empirical mode decomposition based principal component analysis. Computers and Chemical Engineering, Vol. 115, Issue 12, 2018, p. 1-21.
-
Benzi R., Sutera A., Vulpiani A. The mechanism of stochastic resonance. Journal of Physics A: Mathematical and General, Vol. 14, 1981, p. 453-497.
-
Li Jimeng, Chen Xuefeng, He Zhengjia Adaptive stochastic resonance method for impact signal detection based on sliding window. Mechanical Systems and Signal Processing, Vol. 36, Issue 2, 2013, p. 240-255.
-
Han Dongying, Li Pei, An Shujun, et al. Multi-frequency weak signal detection based on wavelet transform and parameter compensation band-pass multi-stable stochastic resonance. Mechanical Systems and Signal Processing, Vol. 70, Issue 71, 2016, p. 995-1010.
-
Lu Siliang, He Qingbo, Zhang Haibin, et al. Rotating machine fault diagnosis through enhanced stochastic resonance by full-wave signal construction. Mechanical Systems and Signal Processing, Vol. 85, 2017, p. 82-97.
-
Ren Litong, Hu Jinhai, Xie Shousheng, et al. Application research of the vibration fault feature extraction based on stochastic resonance pretreatment. Journal of Vibration and Shock, Vol. 33, Issue 2, 2014, p. 141-146.
-
Li Hongkun, Zhang Xiaowen, He Changbo, et al. Weak fault enhancement method for blade crack by using stochastic resonance. Journal of Mechanical Engineering, Vol. 52, Issue 1, 2016, p. 94-101.
-
Li Zhixing, Shi Boqiang Extracting weak fault characteristics with adaptive singular value decomposition and stochastic resonance. Transactions of the CSAE, Vol. 33, Issue 11, 2017, p. 60-67.
-
Lei Yaguo, Han Dong, Lin Jing, et al. New adaptive stochastic resonance method and its application to fault diagnosis. Journal of Mechanical Engineering, Vol. 7, 2012, p. 62-67.
-
Duan Haibin Ant Colony Algorithms: Theory and Application. Science Press, Beijing, 2005.
-
Lei Yaguo, Han Dong, Lin Jing, He Zhengjia Planetary gearbox fault diagnosis using an adaptive stochastic resonance method. Mechanical Systems and Signal Processing, Vol. 38, Issue 1, 2013, p. 113-124.
-
Youhao Xie, Xiaole Liu, Houguang Liu, Gang Cheng, Xihui Chen Improved frequency-shifted and re-scaling stochastic resonance for gear fault diagnosis. Transactions of the Chinese Society of Agricultural Engineering, Vol. 32, Issue 8, 2016, p. 70-76.
-
Li Jimeng, Chen Xuefeng, He Zhengjia Multi-stable stochastic resonance and its application research on mechanical fault diagnosis. Journal of Sound and Vibration, Vol. 332, Issue 22, 2013, p. 5999-6015.
-
Liu Jinjun, Leng Yonggang, Lai Zhihui, et al. Stochastic resonance based on frequency information exchange. Acta Physica Sinica, Vol. 65, Issue 22, 2016, p. 1-14.
-
Leng Yonggang, Wang Taiyong, Qin Xuda, et al. Power spectrum research of twice sampling stochastic resonance response in a bistable system. Acta Physica Sinica, Vol. 53, Issue 3, 2004, p. 717-723.
