Abstract
Solar array drive assembly is an important part of the spacecraft. It is used to rotate the solar panels. The gear assembly in solar array drive assembly plays a key role in transferring power safely. Nonlinear behavior of gear assembly, like the chaotic motion, can highly affect the stability and operating life of solar array drive assembly. Clearances in gear assembly which were neglected for simplification in past years have increased the risk of failure and become a problem in accurate control. To investigate the clearances effect on nonlinear behavior, this paper establishes a new dynamic model of the gear assembly with bilateral clearances. The main difference comparing to general spur gears is its unique hysteresis stiffness may also influence the clearance effects. Transformation of the hysteresis loop is observed from theoretical equations using different parameters. Bifurcations and chaotic analysis of the system are carried out by numerical simulations in this study. The results show that the variation of clearances may induce the chaotic behavior into gear transmission even when the primary response is stable. When the system step into the chaotic region, it has a high risk of unstable vibration and fuzzy output. The influence of excitation frequency on the chaotic motion of the system is also provided. Chaos thresholds are calculated to avoid nonlinear behavior of the system in design and control. This study makes it possible to predict the unstable clearance interval in this system and avoid the system stepping into chaotic motion. Analyzing and predicting the chaotic behaviors can contribute to the further studies on design and control of the solar array drive assembly.
1. Introduction
Chaotic behavior of dynamical systems is one of the challenges in the satellites area. Chaotic motions can increase the difficulty of attitude control and influence the output accuracy of the satellites. Moreover, chaotic motions are highly sensitive to initial conditions. Researches on chaos prediction of the mechanism are very important to satellite’s design and control.
Solar array drive assembly (SADA) is a mechanism designed to actuate solar panels in a satellite. It consists of a motor, a gear assembly and a power transfer assembly. The gear assembly is a key transmission mechanism connecting the main body and output part of the satellite. When the nonlinear motion of the gear assembly occurs, it highly affects the stability of the satellite.
In past years, the failure of the gear transmission in SADA can mainly be divided into two types reviewed by Zhou [1]. One is the stress-strain failure due to the flexible deformation of the gear. The other is the lubricant failure which expends the clearance effects on gear. Rodger [2] pointed out that no signs of deterioration could be detected by tests, but a significant amount of wear had occurred in the gear assembly for the X-ray Timing Explorer spacecraft. Johnson [3] investigated the testing failure of gear assembly for the Mars Reconnaissance Orbiter spacecraft. Researches on the stress-strain analysis of the gear assembly on SADA have been developed for years. Rheaume [4, 5] developed a new three-dimensional FEM of an actual gear to reproduce the behavior. Folega [6] studied an FEM model of the gear with composite material to calculate the result. Dobre [7] described an FEA model with metallic membranes. However, there are few previous researches on the clearance effects of the gear assembly on SADA. The influence of the clearance on the gear assembly was neglected in the past design, because it is very difficult to describe it mathematically. The difference between the gear assembly in SADA and the ordinary spur gear in the transmission device is that the gear assembly in SADA has a nonlinear hysteresis stiffness due to the complex transmission principle using its flexible deformation. The gear assembly in SADA needs to consider the effects of clearance and hysteresis that impact each other. Therefore, previous papers ignored the clearance effects for simplification.
Due to the recent development of satellites, influences of clearance are needed to be considered for higher accuracy. There are several researchers who began to pay attention to the importance of the clearance on the gear assembly in SADA. Legnani [8] studied the effects of elasticity and backlash of the harmonic gears and considered the backlash partially included in the whole positional error and guessed the error to be an approximate periodical function of the input angle. Dhaouadi [9] established a mathematical model and identified its parameters using Genetic Algorithm. Lu [10] studied the tooth profile of harmonic gears. The paper found that the meshing clearance became larger with the increasing modification coefficient. Ostapski [11] gave an analysis of stress state and verified the clearance in the cam-bearing-flex spline of the harmonic gear assebmly. Researches on chaotic analysis of ordinary gears system for various applications have been developed for many years. Wang [12] analyzed the bifurcation and chaos of the gear train by investigating the maximum Lyapunov exponents and Poincare section. Li [13] evaluated the bifurcation and chaos in spur gears system. Sheng [14] provided an understanding of strong nonlinearity in a gear-bearing system, including nonlinear oil-film force and nonlinear gear mesh force. Guo [15] considered uncertainties of a gearbox in wind turbines to evaluate the nonlinear dynamic behavior.
This study is aimed at analyzing the chaotic behavior of a gear assembly in SADA considering bilateral clearances. The difference between the gear assembly and general spur gear is the nonlinear hysteresis stiffness which may also influence the clearance effects. This study attempted to set up an analytical model to investigate the nonlinear chaotic behavior of gear assembly for design. The objectives of this study are a) propose a new dynamic model of the gear assembly with bilateral clearances; b) analyze the effects of clearances on the bifurcation and chaotic behavior under low frequency condition for space environment.
2. Modeling
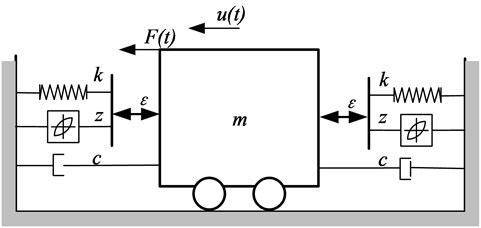
In order to investigate the dynamic behavior of the gear assembly in SADA, a new single-degree-of freedom model is proposed in Fig. 1, in which bilateral clearances are taken into consideration. Due to distinct hysteresis stiffness of gear assembly, a nonlinear spring is used to characterize the hysteresis effect. Hysteresis is the time-based dependence of a system’s output on present and past inputs. The gear assembly has a hysteresis stiffness which means the relation between displacement and external force is not linear. For this reason, we use a variable to express the displacement of the nonlinear spring in Fig. 1. A combination of linear spring and hysteretic spring is built to describe the system’s stiffness. All supports are visualized as solid boundaries. The system motion is supposed along the direction of the displacement.
Fig. 1Model with bilateral clearances
The equation of motion for the system is:
where is the displacement of the system. and are mass and damping coefficients, respectively. is the external force of periodical excitation. is the combination stiffness.
There are some mathematical models to characterize hysteresis. Hassani [16] reviewed some widely used mathematical models, such as Preisach, Krasnosel’skii-Pokrovskii (KP), Prandtl-Ishlinskii (PI), Maxwell-Slip, Bouc-Wen and Duhem. The paper surveyed the expressions, identifications and applications of them. But the study didn’t compare the advantages and disadvantages of these models. According to their applications, these models can mainly be classified into two types. One type is that the model was established from mathematics and used for design. The other type is that the model was established by the control method and used for control. Bouc-Wen model is an analytical hysteresis model, which is widely used in structure application due to its advantage of comprehensible and concise mathematical description. The disadvantage of the Bouc-Wen model is that it is a complicate mathematical model, consequently limits its application for the control field.
Ismail [17] proposed a review of the past, recent developments and implementations of the Bouc-Wen model. Various developments of the Bouc-Wen model are proposed by researchers to model the hysteresis phenomenon in different complex nonlinear structures. Therefore, Bouc-Wen model is chosen to express the hysteresis stiffness of the gear assembly in SADA. In order to investigate the nonlinear effects caused by clearances, we consider the original simple classic Bouc-Wen model to be combined. Based on the classic Bouc-Wen model, the comprehensive stiffness consisting of a linear spring and a hysteretic spring is:
Considering the Bouc-Wen model’s stiffness equation with clearances, is described as:
where is the weighting parameter in the combination. The system will be more nonlinear when the weight becomes lower. is a constant stiffness coefficient. is a constant and positive parameter describing the clearance. is the sign function used to synthesize the discontinuous contact.
The derivative of hysteresis displacement is:
when the gears come into contact, the hysteresis displacement is illustrated by . In Eq. (4), there are five parameters describing the hysteresis loop: , , , and , , and are the hysteresis loop parameters to control the scale and shape of the hysteresis loop. Ismail [17] gives out the relationship between the parameters in the Bouc-Wen model. It shows the model fulfills the second principle of thermodynamics if and only if the following conditions hold:
The hysteresis displacement can be integrated by the differential equations with respect to . The results are in Eqs. (6-9):
Fig. 2Curves of hysteresis loops
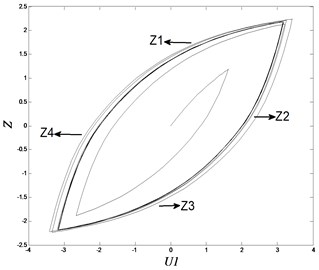
Fig. 3Hysteresis loops with different loop parameters
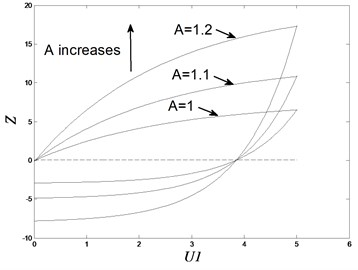
a) Hysteresis loops with different
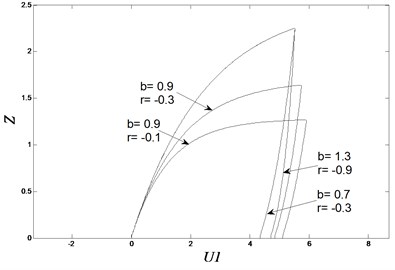
b) Hysteresis loops with different and
Hysteresis loops calculated by hysteresis displacement are illustrated in Fig. 2. Label U1 means the displacement of system . Label Z means the non-observable hysteretic parameter (usually called the hysteresis displacement) . Hysteresis loop parameters , , , are difficult to generate an explicit solution to the shape of loops. Here we observed some of them to see the transformation of loops under their variation. When the value of A becomes larger, curvature increases and the loop becomes long and narrow. The energy loss tends to expand more. and are in complicated relation to the curvature of the loop. Fig. 3 shows the parameter variation effect by drawing the solutions of Eqs. (6-9) to visualize the above conclusion.
3. Numerical results of bifurcation and chaos
In this section, we give the numerical simulation to observe the influence of clearances and low frequency on chaotic behavior of the system. Numerical solution is obtained by using Runge-Kutta algorithm in MATLAB. The initial values of system parameters are as follows:
3.1. Dimensionless excitation frequency
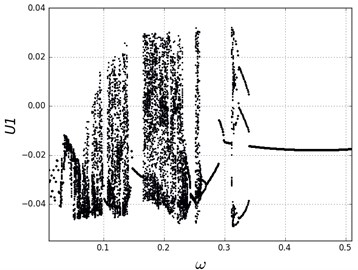
Bifurcation diagram of the system is shown in Fig. 4. Label U1 means the displacement of system . Label means the excitation frequency. The bifurcation parameter is the excitation frequency of the system. It can be observed that the system experiences the variation from periodical motion to chaos under different values of the excitation frequency. Poincare maps and phase diagrams with different frequencies are shown in Fig. 5. The left graphs in each sub-plots of Fig. 5 are Poincare maps. The right graphs are phase diagrams. Label U2 means the derivative of displacement .
Fig. 4Bifurcation diagram with different frequency
Phase diagram is a diagram that indicates the system motion in state space. Poincare map can be interpreted as a discrete dynamical system in math. It is the intersection of a periodic orbit in the state space. Here we plot phase diagram and Poincare map to assist the observation on the periodic system motion under a certain value of excitation frequency. When the system motion is periodic, there is one continuous curve in the phase diagram and one point in the Poincare map. That means the system motion is in the same orbit in every circle of reciprocating movement and multiple-cycle movements present to be one overlapping curve in the phase diagram and one overlapping point in the Poincare map. When the system motion is non-periodic, there are many nonoverlapping curves in the phase diagram and some discrete points in the Poincare diagram.
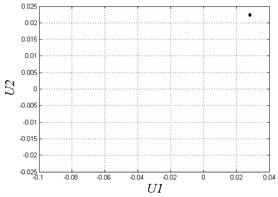
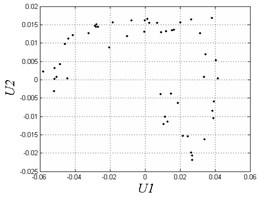
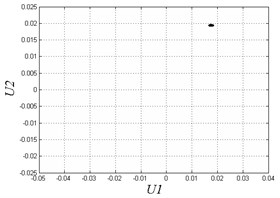
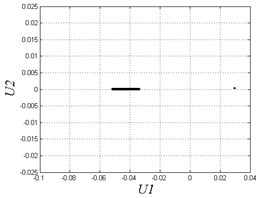
In Fig. 4, when 0.35, the system exhibits 1T-periodic motion in the bifurcation diagram. We observe the Poincare map and phase diagram of 0.45 in Fig. 5(a). The phase curve is an overlapping loop which is non-circular due to the hysteresis property of the solar array gear. The Poincare map is one point to show the motion is periodic under the frequency. However, with the decrease of the excitation frequency, the system becomes unstable and has many chaotic regions. There are some slim chaotic regions and broad chaotic regions. When 0.27, the system steps into chaos. With the decrease of the frequency, it returns to periodic motion. When 0.23 0.18, the system steps into chaos again. To observe some threshold values, we plot Poincare maps and phase diagrams under different frequencies in Fig. 5(b-e). When 0.27, the system motion is chaotic appearing as nonoverlapping curves and some discrete points in the figure. When 0.24, the system returns to periodic motion again with a different continuous phase loop comparing to 0.45. When 0.1 and 0.05, the motion turns into chaos. The system exhibits chaotic behavior when the frequency is very small. This chaotic behavior is also due to the effects of hysteresis in solar array gears. When the frequency is quite small, the system may generate complex oscillations in a circle time of excitation because of the effects of clearances and hysteresis stiffness. In general, the gear assembly in solar array drives works under various excitation frequencies. But most of the working condition is right on low speed. The working condition needs to switch to high frequency only in a short amount of time. Therefore, we better avoid disordered motion at low excitation frequency.
The results indicate that the response of the system is periodic under high excitation frequency, however, it tends to result in chaotic behavior under lower excitation. This validates with the clearance and hysteresis effects the gear assembly can exhibit possible chaotic behavior in the low frequency condition in the space environment. In the control of the system, we better not approach to these chaotic regions. The following part will present the potential clearance effects on the system behavior even when the frequency is in stable regions.
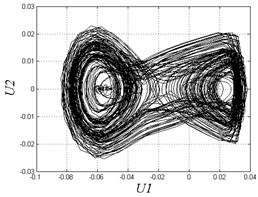
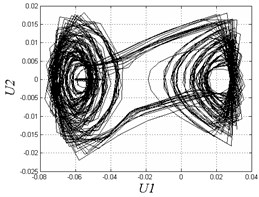
Fig. 5Poincare maps and phase diagrams with different frequencies
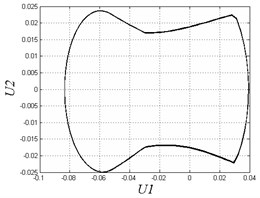
a) 0.45
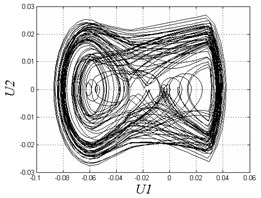
b) 0.27
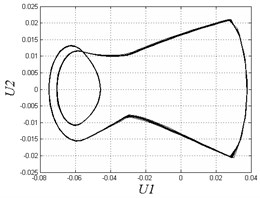
c) 0.24
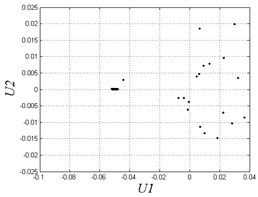
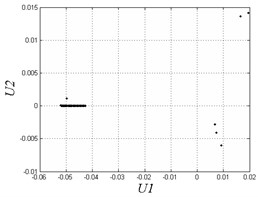
d) 0.1
e) 0.05
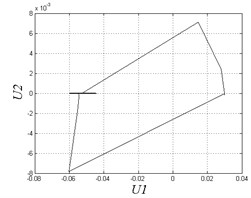
f) 0.001
3.2. Positioning dimensionless clearances
Bifurcation diagram of the system is shown in Fig. 6. Label means the clearance. The bifurcation parameter is the clearance. Here we increase the clearance from 0.001 to 0.03 and set a constant excitation frequency 0.4 which is in the stable region according to the results in Fig. 4. Therefore, clearance is changed to observe the influence of clearance on the system motion.
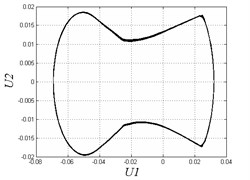
When the clearance is lower than 0.004, the system motion is stable and periodical in Fig. 6. Fig. 7(a) shows the overlapping curve in the phase diagram and one point in the Poincare map when 0.003 that system is in periodic motion. In that situation, we can ignore the clearance effect in system analysis as most previous researches do.
Fig. 6Bifurcation diagram with different clearances
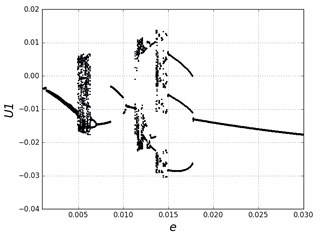
Fig. 7Poincare maps and phase diagrams with different clearances
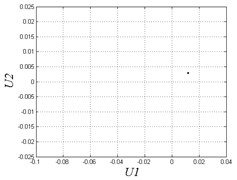
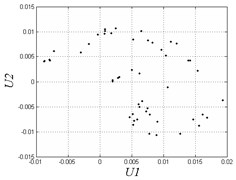
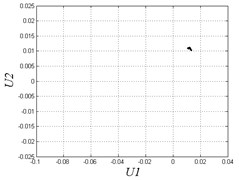
a) 0.003
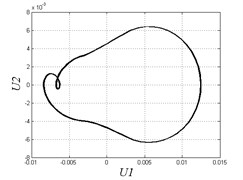
b) 0.007
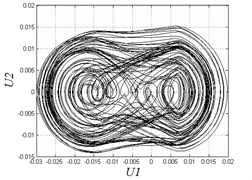
c) 0.012
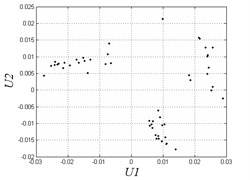
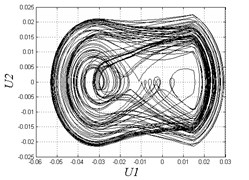
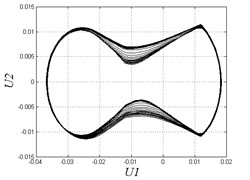
d) 0.015
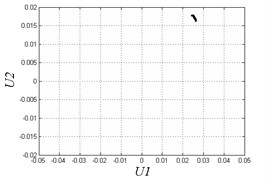
e) 0.025
However, when clearance enlarges, chaotic motion appears. The region in [0.004, 0.007] is disordered and unstable. Fig. 7(b) shows that the Poincare map has some separate points when 0.007. The region in [0.008, 0.012] has period-doubling motion and discontinuity due to the complex combing effects of clearances and hysteresis. From Fig. 7(c) we can see that the motion is periodic in the Poincare map, while the curves in the phase diagram become very different from continuous curves comparing to Fig. 7(a). When the clearance becomes larger and larger, the system transmits to a situation of alternate chaotic region and periodic region. Fig. 7(d) shows under the threshold value 0.015, Poincare map has many separate points and the motion is non-periodic. When is greater than 0.018, the system motion becomes stable and periodical which is impracticable in applications as we don’t need large clearance. Fig. 7(e) also demonstrates the motion is periodic when 0.025.
Taking above bifurcation diagrams, phase curves and Poincare maps into consideration, the response of the system tends to be chaotic motion even when the excitation frequency is in stable regions. When the clearance varies across the intersection of stable and unstable, the chaotic motion occurs. The system responses to the high risk of vibration and fuzzy output. The chaos possibility in gear assembly with clearances for low frequency space application is provided in the above results.
4. Conclusions
A new model of the gear assembly with bilateral clearances is established in this study. The numerical bifurcation analysis is presented. Under the bifurcation parameter of clearance and frequency, the response of the system varies from periodic to chaotic motion. When the frequency is large, the system is stable. However, in the low frequency satellite application, the system tends to get into disordering chaotic motion under the specific frequency intervals. Moreover, when the system is working under the safe frequency, clearance still play a key role in inducing possible chaotic motions. When clearances expand, and go across the threshold into chaos region, the system is switched into an unstable condition which may lead to possible vibrations. In the space environment, vibrations can result in harmful destruction due to the vacuum condition. Therefore, analysis on clearance effects of solar array gear in the design stage and monitor of clearance variation in control stage are both needed to avoid stepping into chaos region. The study results can contribute to further researches on design and control of the gear transmission in satellites application.
References
-
Zhou H., Wen Q., Zhang W. Harmonic drive used in spacecraft. Vacuum and Cryogenics, Vol. 10, Issue 4, 2004, p. 187-192.
-
Rodger F., Son N. Development of the solar array deployment and drive system for the XTE spacecraft. NASA report, No. 27284, 1995, p. 268-282.
-
Johnson M. R., Gehling R., Head R. Failure of harmonic gears during verification of a two-axis gimbal for the mars reconnaissance orbiter spacecraft. Proceedings of the 38th Aerospace Mechanisms Symposium, 2006, p. 38-50.
-
Rhéaume F. E., Champliaud H., Liu Z. Understanding and modelling the torsional stiffness of harmonic drives through finite-element method. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 223, Issue 2, 2009, p. 515-524.
-
Rheaume F. E., Champliaud H., Liu Z. On the computing of the torsional rigidity of a harmonic drive using FEA. International ANSYS Conference, 2006, p. 2-4.
-
Folęga P. Study of dynamic properties of composite and steel-composite flexsplines of harmonic drives. Journal of Vibroengineering, Vol. 17, Issue 1, 2015, p. 155-163.
-
Dobre D., Simion I., Adir V. G. Finite element analysis of the flexible coupling with metallic membranes. Annals of DAAAM and Proceedings, 2010.
-
Legnani G., Faglia R. Harmonic drive transmissions: the effects of their elasticity, clearance and irregularity on the dynamic behaviour of an actual SCARA robot. Robotica, Vol. 10, Issue 4, 1992, p. 369-375.
-
Dhaouadi R., Ghorbel F. H. Modelling and analysis of nonlinear stiffness, hysteresis and friction in harmonic drive gears. International Journal of Modelling and Simulation, Vol. 28, Issue 3, 2008, p. 329-336.
-
Lu Q., Liang Y., Fan Y., et al. Research on tooth profile interference based on meshing simulation of harmonic drive. Journal of System Simulation, Vol. 21, Issue 19, 2009, p. 6317-6320.
-
Ostapski W. Analysis of the stress state in the harmonic drive generator-flexspline system in relation to selected structural parameters and manufacturing deviations. Bulletin of the Polish Academy of Sciences: Technical Sciences, Vol. 58, Issue 4, 2010, p. 683-698.
-
Wang X., Wu S., Sun X., Deng M., Qing M., Li Q., Zhu E. The bifurcation and chaos analyzing of the Nonlinear gear train with backlash. Proceedings of The International Conference on Mechanical Engineering and Mechanics, 2007.
-
Li S., Wu Q., Zhang Z. Bifurcation and chaos analysis of multistage planetary gear train. Nonlinear Dynamics, Vol. 75, Issues 1-2, 2014, p. 217-233.
-
Sheng D., Zhu R., Jin G., et al. Bifurcation and chaos study on transverse-torsional coupled 2K-H planetary gear train with multiple clearances. Journal of Central South University, Vol. 23, Issue 1, 2016, p. 86-101.
-
Gou X. F., Zhu L. Y., Chen D. L. Bifurcation and chaos analysis of spur gear pair in two-parameter plane. Nonlinear Dynamics, Vol. 79, Issue 3, 2015, p. 2225-2235.
-
Hassani V., Tjahjowidodo T., Do T. N. A survey on hysteresis modeling, identification and control. Mechanical systems and signal processing, Vol. 49, Issue 1, 2014, p. 209-233.
-
Ismail M., Ikhouane F., Rodellar J. The hysteresis Bouc-Wen model, a survey. Archives of Computational Methods in Engineering, Vol. 16, Issue 2, 2009, p. 161-188.
-
Saghafi A., Farshidianfar A. An analytical study of controlling chaotic dynamics in a spur gear system. Mechanism and Machine Theory, Vol. 96, Issue 1, 2016, p. 179-191.
-
Lin H., Wang S., Dowell E. H., Dong J. Bifurcation observation of combining spiral gear transmission based on parameter domain structure analysis. Mathematical Problems in Engineering, Vol. 2016, 2016, p. 3738508.
-
Chang-Jian C. W. Strong nonlinearity analysis for gear-bearing system under nonlinear suspension-bifurcation and chaos. Nonlinear Analysis-Real World Applications, Vol. 11, Issue 3, 2010, p. 1760-1774.
-
Chang-Jian C. W. The bifurcation and chaos of a gear pair system based on a strongly non-linear rotor-bearing system. Proceedings of the Institution of Mechanical Engineers Part C – Journal of Mechanical Engineering Science, Vol. 224, Issue 9, 2010, p. 1891-1904.
-
Gao H., Zhang Y. Nonlinear behavior analysis of geared rotor bearing system featuring confluence transmission. Nonlinear Dynamics, Vol. 76, Issue 4, 2014, p. 2025-2039.
-
Yoon J., Lee H. Dynamic vibratory motion analysis of a multi-degree-of-freedom torsional system with strongly stiff nonlinearities. Proceedings of the Institution of Mechanical Engineers Part C –Journal of Mechanical Engineering Science, Vol. 229, Issue 8, 2015, p. 1399-1414.
-
Beyaoui M., Tounsi M., Abboudi K., Feki N., Walha L., Haddar M. Dynamic behaviour of a wind turbine gear system with uncertainties. Comptes Rendus Mecanique, Vol. 344, Issue 6, 2016, p. 375-387.
-
Tounsi M., Beyaoui M., Abboudi K., Feki N., Walha L., Haddar M. Influence of uncertainty in aerodynamic performance on the dynamic response of a two-stage gear system. Journal of Theoretical and Applied Mechanics, Vol. 54, Issue 2, 2016, p. 601-612.
-
Ismail M., Ikhouane F., Rodellar J. The hysteresis Bouc-Wen model, a survey. Archives of Computational Methods in Engineering, Vol. 16, Issue 2, 2009, p. 161-188.
-
Hossain M. Z., Mizutani K., Sawai H. Chaos and multiple periods in an unsymmetrical spring and damping system with clearance. Journal of Sound and Vibration, Vol. 250, Issue 2, 2002, p. 229-245.
-
Zukovic M., Cveticanin L. Chaos in non-ideal mechanical system with clearance. Journal of Vibration and Control, Vol. 15, Issue 8, 2009, p. 1229-1246.
-
Gupta T. C., Gupta K., Sehgal D. K. Nonlinear dynamics and chaos of an unbalanced flexible rotor supported by deep groove ball bearings with radial internal clearance. IUTAM Symposium on Emerging Trends in Rotor Dynamics, p. 321-333.
About this article
The authors would like to acknowledge the financial support from the National Natural Science Foundation of China (Grant No. 11372176).
