Abstract
The lateral response, energetics and stability of the cable-guided hoisting system that differs from the rail-guided, such as elevator systems, is investigated in this paper. While the equations of motion are established by Hamilton's principle, the boundary conditions are obtained to calculate the natural frequencies with the modified velocity of wave propagation. Then, the governing equation is transformed into a set of ordinary differential equations through the Galerkin method and the rate of change in the energy is derived from the control volume viewpoint. The system frequencies, response of each order and energy characteristics are analyzed. The results show that the system frequencies first decrease, and then increase with the increase of the length and demonstrate that the modified velocity of wave propagation is reasonable by comparison of three approaches. The presented method proves to be effective to obtain the response of each order. According to Lyapunov’s second method, the rate of change in the energy indicates the cable-guided hoisting system experiences stability and instability during downward and upward movements, respectively.
1. Introduction
Cables, due to their light weight and the ability to resist relatively large axial load, have been widely employed in diverse engineering applications including crane loading [1], suspension bridges [2], cable-driven parallel robots [3] and elevators [4, 5], along with mine hoisting [6], however, they are subjected to the vibrations caused by the external excitations for their high flexibility. Particularly, in the typical sinking winch mechanism [7], as shown in Fig. 1(a), cables play a vital role not only in hoisting but also in guiding. The mechanism used to sink the vertical shaft is composed of winches, head sheaves, a derrick, a hoisting bucket, a construction platform and three main types of cables: suspension cables, guide cables and a hoisting cable, in which the platform is hung by two suspension cables and two guide cables while the bucket is held by one hoisting cable and supported by two guide cables. Since the lateral movement of the platform is completely restricted by self-locking of the wedge block, the majority of the mechanism can be equivalently modelled as the cable-guided hoisting system, which is shown in Fig. 1(b). The similar configuration is also adopted in mine hoisting (for example, skip or cage hoisting). An important feature of the system is that the length of the hoisting cable and the lateral stiffness of the guide cables are both of time-varying nature. Additionally, the tension in the guide cables should be properly designed to meet the safety and performance requirements.
The longitudinal and lateral vibrations of hoisting cables have been studied by many researchers for decades. Chi and Shu [8] discussed the natural frequencies associated with the longitudinal vibration of an elevator system considering various boundary conditions. Kaczmarczyk [9] established the longitudinal model of the catenary-vertical hoisting cable system with a periodic excitation to analyze the passage through resonances. Ren and Zhu [10] investigated the longitudinal vibration of a moving cable-car system, in which the lower end of the cable is connected to the car through a spring and a damper. Zhu and Xu [11] studied the lateral vibrations of stationary and moving cables using the taut string and tensioned beams with pinned and fixed boundaries. Zhu and Chen [12] conducted the challenging experiments on a novel scaled elevator to validate the theoretical predictions for the uncontrolled and controlled lateral responses of a moving cable in a high-rise elevator. Bao et al. [13] calculated the natural frequencies of the lateral vibration of elevator during downward and upward movements. Kaczmarczyk [14] and Zhang [15] analyzed the longitudinal-lateral coupled vibrations of cables subjected to the external excitations in the mine hoisting and elevator, respectively. However, the scope of above studies was limited to the cases with rigid guide rails. By contrast, this study concentrates on the lateral vibration of the cable-guided hoisting system.
Fig. 1Cable-guided hoisting system
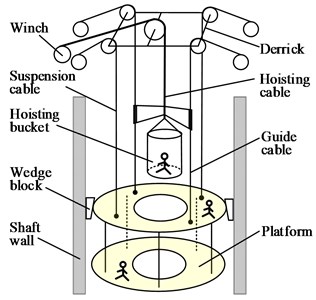
a) Sinking winch mechanism
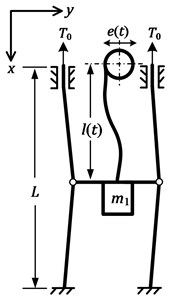
b) Schematic diagram
Much research has made a contribution to the spatial discretization of distributed-parameter structures, such as cables, belts and beams. Meirovitch [16] first proposed the assumed modes method (AMM), which is usually used for spatial discretization of a cable, where trial functions satisfy geometric matching conditions. Wang et al. [17] used the AMM to obtain the lateral response of the cable-guided hoisting system by transferring the guide cables to the hoisting mass. Wang et al. [18] introduced the finite element method (FEM) to investigate the three-dimensional underwater vibrations of a geometrically non-linear cable with a weight at the lower end. Subsequently, Moustafa [19] and Du [20] applied the FEM to the dynamics of cables in overhead cranes and cable-driven parallel manipulators, respectively. Patera [21] first presented the spectral element method, which partitions a structure into elements and applies the spectral method on each element. Considering that the convergence is not in the strong sense in the above methods, recently, Zhu and Ren [22] developed an accurate spatial discretization and substructure method to calculate dynamic responses of one-dimensional structural systems, which consist of length-varying distributed-parameter components and lumped-parameter components. Although these methods can obtain the overall responses of the hoisting cable, it is necessary to analyze the response of each order in the cable-guided hoisting system so that one can observe the specific resonances, which is beneficial for the vibration control.
A greatly amplified vibratory energy can be induced by a small disturbance in the hoisting cable, thus, several researchers have studied the energetics and stability, especially in elevator systems. Bao et al. [13] analyzed the stability of the hoisting cable. The elevator cable experiences instability and the natural frequencies increase during upward movement; whereas the opposite during downward movement. For different elevator operation conditions, Benosman [23] proposed several nonlinear controllers based on Lyapunov theory to stabilize the rope sway and illustrated the stability and performance of the controllers. Dai et al. [24] developed an active control strategy based on the fuzzy sliding mode control for controlling the large-amplitude vibrations of an extending nonlinear elastic cable.
To address the lacks of research in the aspect of cable-guided hoisting system, the present investigation focuses on the lateral response of the hoisting mass and the energy characteristics of the system and aims at obtaining the accurate response of each order. This paper is organized as follows. In Section 2, while the equation governing the lateral vibration of the cable-guided hoisting system is established by Hamilton's principle, the boundary conditions are obtained and used to calculate the natural frequencies with the modified velocity of wave propagation. Then, the governing equation is transformed into a set of ordinary differential equations through the Galerkin method. Section 3 derives the expressions of the energy and the rate of change in the energy. Section 4 presents the frequency and energy characteristics by comparing with the rail-guided hoisting system and analyzes the response of each order. Finally, Section 5 draws conclusions.
2. Mathematical model
The lateral vibration of the cable-guided hoisting system shown in Fig. 1(b) is investigated, where the length of the hoisting cable at time is and the length of the guide cable is . The hoisting mass is attached to the lower end of the hoisting cable and supported by two guide cables, in which the preloads are both . The displacement of the upper end of the hoisting cable denotes the external excitation in direction that can arise from the eccentricity and misalignment of the head sheave. The hoisting cable has a translating velocity and acceleration in direction, where the overdot denotes time differentiation. The displacements and represent the lateral vibrations of the hoisting cable and the guide cables in the direction, respectively. For notational convenience, instead of and and are used, and similar abbreviations are employed subsequently. The assumptions in Ref. [17] are considered.
2.1. Equation of motion
The kinetic and potential energies of the system are:
where and are the linear density of the hoisting and guide cables, respectively. The terms and are the tension at position of the cables and given as:
The strain and can be approximated as:
Substitute Eqs. (1), (2) into the Hamilton’s principle:
The lateral vibration of the hoisting cable is governed by:
The boundary conditions are obtained as:
where the equivalent mass and stiffness are expressed as:
The governing Eq. (6) with time dependent boundary conditions Eq. (7) should be transformed into one with homogeneous boundary conditions [23]. The lateral displacement can be expressed in the form:
Setting:
yields the homogeneous boundary conditions for . It is reasonable to assume that the lateral displacement from excitation varies from at the upper end of the hoisting cable to zero at the lower end uniformly. Thus, the absolute displacement is defined to be a first-order polynomial in and expressed as:
By Eq. (9), Eqs. (6) and (7) become:
where .
2.2. Natural frequency
Considering , the dynamic response of the hoisting system is approximated by the expansions [14]:
where are the natural frequencies of system and , , can be obtained by the initial and boundary conditions.
Substitution of Eq. (14) into Eq. (13) yields one transcendental equation:
where . In general, the velocity of wave propagation in the wave equation derived from the string model with constant tension is , however, in most cases of the cable-guided hoisting system, the ratio of tensions at both ends of the hoisting cable varies from 1:1 to 3:1 or even higher during the whole winding cycles. Thus, the velocity need to be improved to apply to the time-dependent tension. In a micro length , the tension can be considered to be constant and the propagation time is . In order to ensure that the total propagation time is unchanged, is modified as:
where the main tension is given by Eq. (3).
An accurate method of solving the natural frequencies of an elevator system is presented in Ref. [13], and the frequencies from both methods will be compared in the following. Although the method widely used in the elevator system is also applied to the cable-guided hoisting system in calculating the natural frequencies and the overall responses, it cannot obtain the real response of each order, which is necessary for the vibration control.
2.3. Spatial discretization
Galerkin method is employed to discretize the partial differential Eq. (12) into a set of ordinary differential equations, and the solution for can be approximated in the form:
where are the generalized coordinates and is the number of included modes.
The partial derivatives of with respect to and are:
The derivatives of the natural frequencies with respect to are obtained through differentiation of the boundary condition Eq. (7), and are calculated as:
where:
Substituting Eqs. (18)-(22) into Eq. (12), multiplying the equation by and integrating it from 0 to yields the discretized equation as follows:
where , , and are the mass, damping, stiffness matrices, and the force vector, respectively. Entries of the matrices and the force vector are formulated as:
3. Energy and rate of change in energy
The energy of lateral vibration is:
where:
is the energy density associated with the lateral vibration of the hoisting cable.
Substituting Eqs. (9) and (17) into Eq. (25) yields the discretized expression of the vibration energy:
where:
In order to probe deeply into the stability characteristics of the cable-guided hoisting system, Lyapunov’s second method is utilized. The stability of the system can be determined by the time derivative of the energy . The system is stable if is always negative, otherwise unstable. The rate of change in the vibration energy in Eq. (25) with the control volume approach is obtained by differentiating Eq. (25) and using Leibnitz’s formula:
Use of the governing Eq. (12) and application of the integration by parts yields:
The first and fourth terms on the right hand are positive and negative definite during downward ( 0) and upward ( 0) movement of the cable, respectively. The second term is negative and positive definite during downward and upward movements, competing with the effect of the fourth term. The last term indicates that a positive and negative jerk has a stabilizing and destabilizing effect, respectively.
Similar to Eq. (27), the discretized expression of Eq. (30) is derived:
where:
4. Results and discussion
Numerical simulations are applied to the cable-guided hoisting system, the parameters of which are as follows: 1.8 kg/m, 1 kg/m, 530 kg, 395 m and 3×104 N. The downward movement profiles are plotted in Fig. 2, where the maximum velocity and acceleration are 6 m/s and 0.75 m/s2, respectively. The initial length of the hoisting cable is 5 m and the external excitation is given by m. The total simulation time is 73 s and the time step size is 0.01 s.
Fig. 2Downward movement profiles
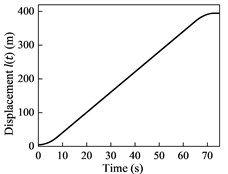
a) Displacement
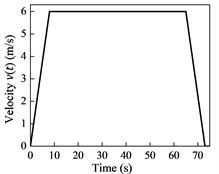
b) Velocity
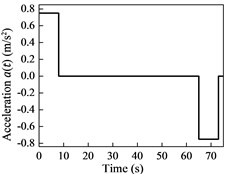
c) Acceleration
4.1. Analysis of frequency
The boundary condition Eq. (7) can be used to predict and analyze the important resonance phenomena. As is shown in Fig. 3, the first six natural frequencies of the hoisting system are calculated from three different approaches and the horizontal line denotes the external excitation frequency. Note that there are significant differences between the modified and the constant , while the frequencies obtained by the modified are in excellent agreement with that calculated by the approach presented in Ref. [13]. Therefore, the modified is suitable for the hoisting system with time-varying length and can be used in Eq. (17).
Fig. 3The first six order natural frequencies with length increment
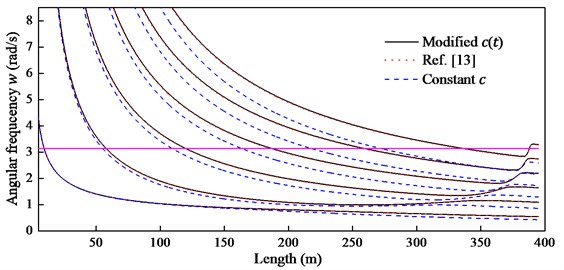
Fig. 4Comparison of natural frequencies between the cable-guided and rail-guided hoisting systems
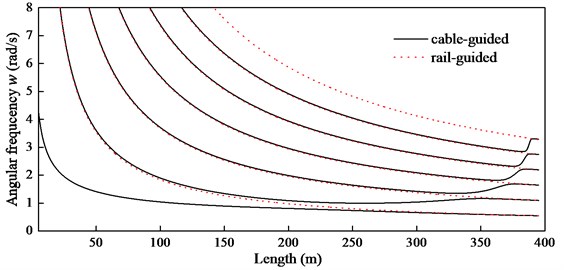
When the equivalent stiffness in Eq. (8) is increased to infinity (i.e., 108N/m) and keeps constant, the cable-guided hoisting system can be considered as the rail-guided one, such as an elevator system, because the guide cable looks like the rigid guide rail. Therefore, the lateral frequencies of the rail-guided hoisting system are calculated by the approach in Ref. [13] to compare with those of the cable-guided hoisting system. As is shown in Fig. 4, in the rail-guided hoisting system the frequencies decrease with the increasing length of the hoisting cable, however, in the cable-guided hoisting system the frequencies first decrease, and then increase with the increase of length. Obviously, the difference on the trend results from the lateral stiffness of the guide. While the lateral stiffness of the rail guide is constant, the stiffness of the cable guide is time-varying and shaped like the letter “U”. In other words, the lateral stiffness defined by Eq. (8) becomes larger and larger when approaches to 0 or from . Essentially, the system frequencies in the cable-guided hoisting system can be decomposed into the frequencies of the hoisting cable and that of the mass supported by the cable guides. In particular, there are two neighboring resonance zones in the sixth order frequency.
4.2. Lateral response
The lateral displacements of the hoisting mass and the cable particle located at 30 m are calculated using Newmark- method with the mode number 20 and shown in Fig. 5. For the time history response of the hoisting mass in Fig. 5(a), it is reasonable that the lateral displacement first increases and then decreases due to the effect of the time-varying stiffness. For the displacement of the cable particle in Fig. 5(b), the reason why the displacement is zero at the beginning is that the particle in the hoisting cable has not been reeled out until 8.17 s.
Fig. 5The lateral displacements of a) the hoisting mass and b) the cable particle
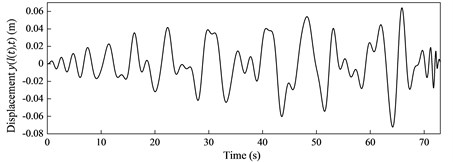
a)
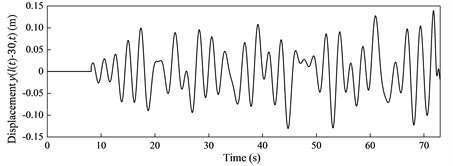
b)
Fig. 6Plots of the generalized coordinates
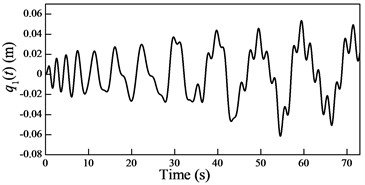
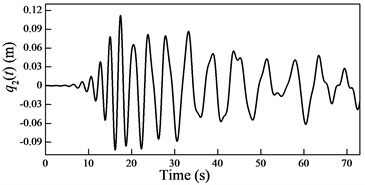
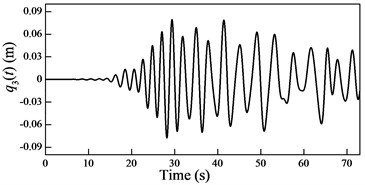
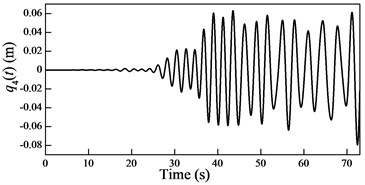
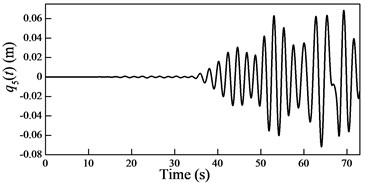
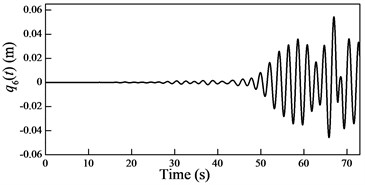
In the cable-guided hoisting system, the natural frequencies slowly vary with the length of the hoisting cable and are widely spaced, thus, there are many resonance zones during downward movement. It is important to investigate the role of each order in the total response in order to control the vibration. Because in the rail-guided hoisting system the geometric matching condition are and , the AMM, where the trial functions happen to be the real mode functions [13], can obtain not only the overall response but also the response of each order. However, in the cable-guided hoisting system the trial function cannot satisfy the force balance relation in the boundary condition Eq. (7), which results in the shortcoming of the AMM in obtaining the response of each order. The generalized coordinates are obtained by solving the equation of motion Eq. (23) with the real mode functions, as shown in Fig. 6. It is evident that each generalized coordinate corresponds to the specific resonance location shown in Fig. 3. Particularly, in Fig. 6 there are two resonances in , which corresponds to the sixth order frequency in Fig. 3. In addition, one can notice that the amplitude of each generalized coordinate has the same order of magnitude.
4.3. Energy characteristics
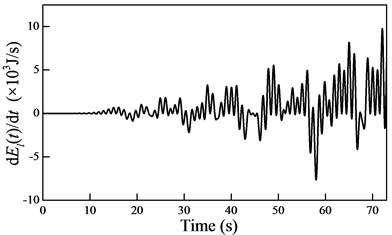
Substituting the generalized coordinates obtained from Eq. (23) into Eqs. (27) and (31) yields the energy and the rate of change in the energy under the external excitation, as shown in Fig. 7.
Fig. 7a) The energy and b) the rate of change in the energy

a)
b)
In order to determine the stability of the cable-guided hoisting system, the free vibration is investigated. Considering the distributed initial displacement m and setting the excitation 0 yields the rate of change in the energy, as shown in Fig. 8.
Fig. 8The rate of change in the energy during a) downward and b) upward movements
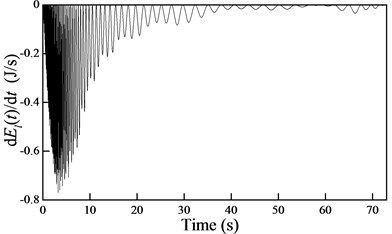
a)
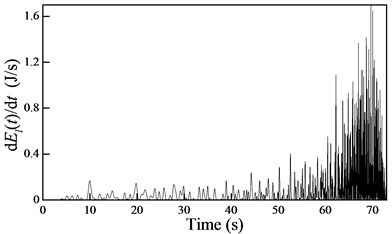
b)
Fig. 8 shows that the rate of change in the energy is always negative and positive during downward and upward movements, respectively. According to Lyapunov’s second method, the cable-guided hoisting system experiences stability and instability during downward and upward movements, respectively, which is consistent with the rail-guided hoisting system.
5. Conclusions
In this study, the lateral response of a moving hoisting conveyance guided by cables with both ends fixed is investigated. The equation governing the lateral vibration of the cable-guided hoisting system is established by Hamilton’s principle and transformed into a set of ordinary differential equations through the Galerkin method. Further, the rate of change in the energy is derived from the control volume viewpoint. The following conclusions could be drawn:
1) The natural frequencies of the cable-guided hoisting system are calculated from the boundary conditions with the modified velocity of wave propagation and then compared with other two approaches. The excellent agreement with the exact solution indicates that the modified is reasonable and suitable for the hoisting system with time-varying length and can be employed in the mode functions. Comparing the cable-guided hoisting system with the rail-guided, it is observed that the natural frequencies in the former first decrease and then increase with the increase of length while the frequencies in the latter gradually decrease.
2) When the external excitation frequency coincides the slowly varying frequencies of the cable-guided hoisting system, the lateral resonances occur during downward movement, which is validated by the response of each order obtained by the presented method. There are two resonances in the sixth order response and the amplitudes of the first six generalized coordinates have the same order of magnitude.
3) The cable-guided hoisting system experiences stability and instability during downward and upward movements, respectively, which is the same as the rail-guided hoisting system.
References
-
Qian S., Zi B., Zhang D., Zhang L. Kinematics and error analysis of cooperative cable parallel manipulators for multiple mobile cranes. International Journal of Mechanics and Materials in Design, Vol. 10, Issue 4, 2014, p. 395-409.
-
Wang Z. Q., Kang H. J., Sun C. S., Zhao Y. B., Yi Z. P. Modeling and parameter analysis of in-plane dynamics of a suspension bridge with transfer matrix method. Acta Mechanica, Vol. 225, Issue 12, 2014, p. 3423-3435.
-
Khosravi M. A., Taghirad H. D. Robust PID control of fully-constrained cable driven parallel robots. Mechatronics, Vol. 24, Issue 2, 2014, p. 87-97.
-
Askari H., Younesian D., Saadatnia Z. Nonlinear oscillations analysis of the elevator cable in a drum drive elevator system. Advances in Applied Mathematics and Mechanics, Vol. 7, Issue 1, 2015, p. 43-57.
-
Arrasate X., Kaczmarczyk S., Almandoz G., Abete J. M., Isasa I. The modelling, simulation and experimental testing of the dynamic responses of an elevator system. Mechanical Systems and Signal Processing, Vol. 42, Issue 1-2, 2014, p. 258-282.
-
Wang D. G., Zhang D. K., Ge S. R. Effect of terminal mass on fretting and fatigue parameters of a hoisting rope during a lifting cycle in coal mine. Engineering Failure Analysis, Vol. 36, 2014, p. 407-422.
-
Shao X. G., Zhu Z. C., Wang Q. G., Chen P. C., Zi B., Cao G. H. Non-smooth dynamical analysis and experimental validation of the cable-suspended parallel manipulator. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 226, Issue 10, 2012, p. 2456-2466.
-
Chi R. M., Shu H. T. Longitudinal vibration of a hoist rope coupled with the vertical vibration of an elevator car. Journal of Sound and Vibration, Vol. 148, Issue 1, 1991, p. 154-159.
-
Kaczmarczyk S. The passage through resonance in a catenary–vertical cable hoisting system with slowly varying length. Journal of Sound and Vibration, Vol. 208, Issue 2, 1997, p. 243-269.
-
Ren H., Zhu W. D. An accurate spatial discretization and substructure method with application to moving elevator cable-car systems-part II: Application. Journal of Vibration and Acoustics, Transactions of the ASME, Vol. 135, Issue 5, 2013, p. 051037.
-
Zhu W. D., Xu G. Y. Vibration of elevator cables with small bending stiffness. Journal of Sound and Vibration, Vol. 263, Issue 3, 2003, p. 679-699.
-
Zhu W. D., Chen Y. Theoretical and experimental investigation of elevator cable dynamics and control. Journal of Vibration and Acoustics, Transactions of the ASME, Vol. 128, Issue 1, 2006, p. 66-78.
-
Bao J. H., Zhang P., Zhu C. M., Sun W. Transverse vibration of flexible hoisting rope with time-varying length. Journal of Mechanical Science and Technology, Vol. 28, Issue 2, 2014, p. 457-466.
-
Kaczmarczyk S., Ostachowicz W. Transient vibration phenomena in deep mine hoisting cables. Part 1: Mathematical model. Journal of Sound and Vibration, Vol. 262, Issue 2, 2003, p. 219-244.
-
Zhang P., Zhu C. M., Zhang L. J. Analysis of forced coupled longitudinal-transverse vibration of flexible hoisting systems with varying length. Engineering Mechanics, Vol. 25, Issue 12, 2008, p. 202-207.
-
Meirovitch L. Analytical Methods in Vibrations. Macmillan, London, 1967.
-
Wang J. J., Cao G. H., Zhu Z. C., Wang Y. D., Peng W. H. Lateral Response of Cable-Guided Hoisting System with Time-Varying Length: Theoretical Model and Dynamics Simulation Verification. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2015.
-
Wang P. H., Fung R. F., Lee M. J. Finite element analysis of a three-dimensional underwater cable with time-dependent length. Journal of Sound and Vibration, Vol. 209, Issue 2, 1998, p. 223-249.
-
Moustafa K. A. F., Gad E. H., EI-Moneer A. M. A., Ismail M. I. S. Modelling and control of overhead cranes with flexible variable-length cable by finite element method. Transactions of the Institute of Measurement and Control, Vol. 27, Issue 1, 2005, p. 1-20.
-
Du J. L., Cui C. Z., Bao H., Qiu Y. Y. Dynamic analysis of cable-driven parallel manipulators using a variable length finite element. Journal of Computational and Nonlinear Dynamics, Vol. 10, Issue 1, 2015, p. 1-20.
-
Patera A. T. A spectral element method for fluid dynamic: laminar flow in a channel expansion. Journal of computational physics, Vol. 54, 1984, p. 468-488.
-
Zhu W. D., Ren H. An accurate spatial discretization and substructure method with application to moving elevator cable-car systems-part I: Methodology. Journal of Vibration and Acoustics, Transactions of the ASME, Vol. 135, Issue 5, 2013, p. 051036.
-
Benosman M. Lyapunov-based control of the sway dynamics for elevator ropes. IEEE Transactions on Control Systems Technology, Vol. 22, Issue 5, 2014, p. 1855-1863.
-
Dai L., Sun L., Chen C. Control of an extending nonlinear elastic cable with an active vibration control strategy. Communications in Nonlinear Science and Numerical Simulation, Vol. 19, Issue 10, 2014, p. 3901-3912.
About this article
This work is supported by the National Natural Science Foundation of China (51475456), the National Key Basic Research Program of China (2014CB049404), the Fundamental Research Funds for the Central Universities (2013QNB12), and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
