Abstract
The position tracking control problem of the electric cylinder is addressed under the influence of nonlinear factors such as friction and disturbance in this paper. First, the dynamic model of electric cylinder is established based on LuGre friction model. Secondly, a nonlinear observer is designed to compensate the friction of servo system. Finally, an adaptive robust controller based on discontinuous projection mapping is proposed to deal with the parameter uncertainty and guarantee the robust performance. The co-simulation results based on Matlab and Recurdyn show that the proposed controller has high control precision and strong robustness.
Highlights
- An adaptive robust controller is designed to compensate the friction torque and other nonlinear factors of the electric cylinder
- The LuGre model was used to model the friction nonlinearity of the system, a nonlinear observer was designed to observe the immeasurable friction state inside the model and a parameter adaptive law was designed to estimate the uncertain parameters
- For parameter compensation errors and external disturbances, the linear and nonlinear robust terms were designed
1. Introduction
With the rapid development of electromechanical coupling technology, the servo system based on electric cylinder has been widely used. Therefore, It is particularly important to realize the high precision control of the electric cylinder [1]. Low speed performance is one of the core indexes of servo system. Friction nonlinearity has the most obvious effect on servo system in low speed stage. With the increase of control precision requirement of servo system, it is very important to choose the appropriate control strategy to solve the problem of nonlinear friction [2].
At present, there are two methods to compensate the nonlinear friction. One is to treat the friction as external interference directly, and improve the anti-interference ability of the system to suppress the impact of friction by improving the control strategy [3]. The other is to eliminate the impact of friction link on the system by feedforward compensation based on friction model [4]. Generally, the first method is easily affected by the coupling of various nonlinear factors, so it cannot accurately compensate the friction nonlinearity. Moreover, a more accurate algorithm is difficult to be applied to engineering practice, and the increase of disturbance will lead to the increase of feedback gain, resulting in the decrease of control performance. The second method describes and predicts the friction phenomenon by establishing an accurate mathematical model, which can accurately compensate the friction nonlinearity and is easy to be applied in engineering practice. The research of friction has shifted from static modeling to dynamic modeling for better characterizing the force of friction [5]. Various dynamic friction models have been proposed [6], the LuGre friction model is the most widely used among them [7]. In addition, the LuGre model is closer to the real friction phenomenon, so the friction nonlinearity of electric cylinder is modeled based on LuGre friction model.
Considering that the internal friction state of LuGre model cannot be measured directly and the friction coefficient is usually unknown, a nonlinear observer is designed in this paper to observe the internal friction state, besides, a parameter adaptive law is designed to estimate the friction coefficient, moment of inertia and other uncertain parameters. Finally, the robust term is introduced to overcome other external disturbances and improve the system stability. The co-simulation results show that the system has good tracking performance and engineering application performance.
2. Problem formulation and nonlinear models
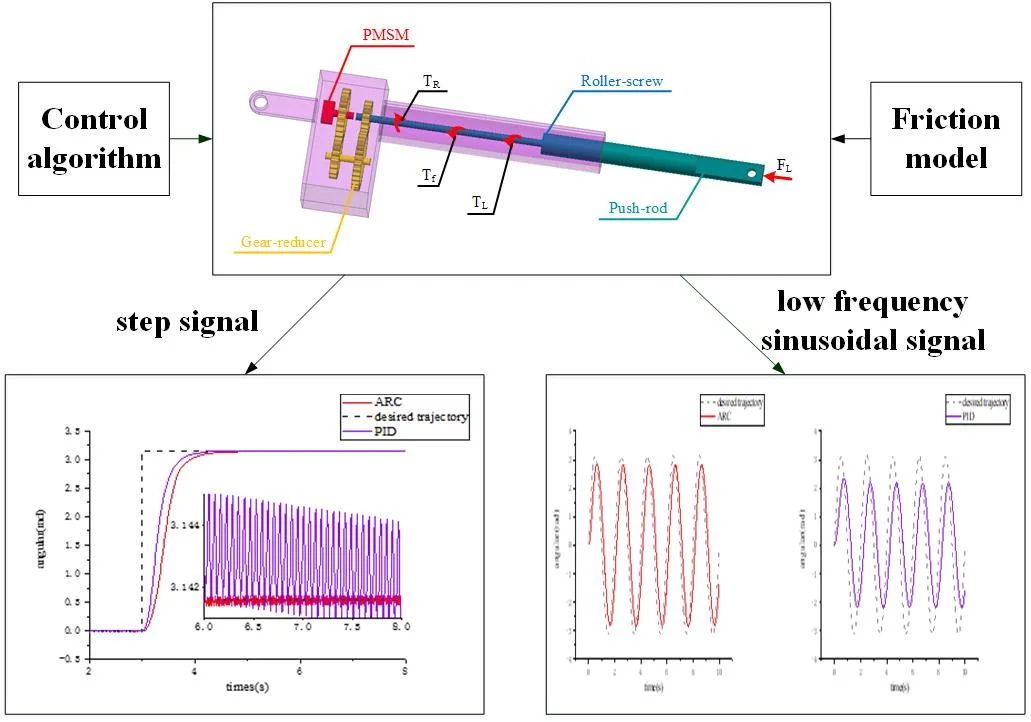
The basic structure of electric cylinders can be shown in Fig. 1, where , , and respectively represent the input torque of Roller-screw, friction torque, load torque, and load force on the cylinder. The torque equation holds:
where and are the inertia and rotation velocity of the screw, denotes disturbance torque.
As and are respectively generated by the action of PMSM output torque and load force, The Eq. (1) can be transformed to:
where and are the rotation displacement and velocity of the PMSM, , and respectively represent the motor-torque ratio, load-torque ratio and control input.
Fig. 1Basic structure of electric cylinders
With the LuGre model [7], the friction torque in Eq. (3) can be written as:
where , and are the bristle stiffness coefficient, bristle damping coefficient and viscous friction coefficient of the system. represents the average deformation of bristle, which is an unmeasurable internal friction state. The function is positive and describes the Stribeck effect. , and respectively represent the levels of the Coulomb friction, static friction force and the Stribeck velocity. is relative velocity. For all , it can be shown that is bounded, and therefore the friction generated by is bounded.
3. Controller design
From Eq. (3) and Eq. (4), As motor rotation displacement and velocity are defined as system state , the entire system can be expressed in a state-space form as:
Define:
where and Besides, and is known.
Then Eq. (5) can be transformed to:
The idea of backstepping design is adopted to design the adaptive robust controller for the nonlinear factors such as friction, clearance and disturbance.
1) Design virtual control variable .
The desired motion trajectory and actual motion trajectory are respectively set to and . The position tracking error and the velocity tracking error are defined by:
where is the positive feedback gain.
2) Design nonlinear observer.
Since the internal friction state in the Lugre model adopted for system modeling cannot be measured, the friction force must be estimated by observation. For this reason, a nonlinear friction observer is designed [8]:
where is learning gain and denotes the estimate of and denotes the estimation error, which is defined by , and the discontinuous projection mapping is defined as:
3) Design control input .
From Eqs. (7) (8) (9), the function can be re-written as:
From Eq. (11), the control input can be designed as:
where , , and respectively represent the model compensation term, robust control law, linear stabilization term and robust feedback term. is the positive feedback gain.
From Eq. (12), Eq. (13) can be transformed to:
where and .
Parameter adaptive law is designed as:
where is a positive definite diagonal matrix.
4) Design nonlinear robust term .
To stabilize the system, design to satisfy the following stabilization conditions:
where is any small and constant positive number.
A design example satisfying Eq. (15) is given [9]:
4. Simulations
Co-simulation is implemented by inputting control signal in Simulink to derive the virtual prototype model of electric cylinder in Recurdyn. First, we import the 3D model of electric cylinder into Recurdyn and establish the appropriate constraints. The friction and contact collision of multiple bodies are defined by the Recurdyn function module. Secondly, we transform the target trajectory into control input by the proposed control algorithm written in S-Functions of Simulink. Finally, control input is applied to the motor output shaft in form of rotational axial force in the Recurdyn environment and motor rotation displacement and velocity are fed back as date information to S-Function of Simulink.
In order to verify the effectiveness of the proposed control strategy, the tracking performance of PID control and ARC control is compared when the desired trajectory of the system is step signal and low frequency sinusoidal signal respectively.
Fig. 2Step signal tracking curve
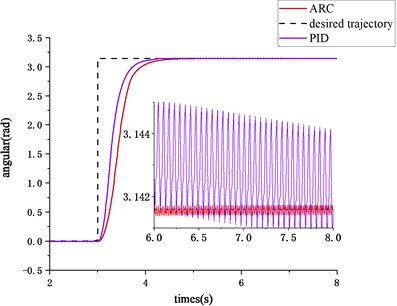
As shown in the Fig. 2, when the desired trajectory is step signal, the tracking response time of PID and ARC are both about 1.5 s. However, ARC has a smoother transition than PID, so less cost of control is required. Besides, as a comparison, when the control system becomes stable, the ARC based system has a smaller amplitude of fluctuation near the target trajectory. Which indicates that ARC has the best performance index, and the average performance index is obviously better than PID due to the accurate observation of the internal state of the friction model, and considering the interference and parameter uncertainty.
Fig. 3Low frequency sinusoidal signal tracking curve
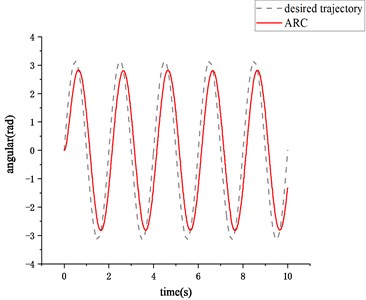
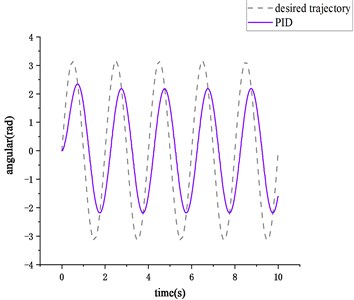
As shown in Fig. 3, when the desired trajectory is low frequency sinusoidal signal, the tracking response time of ARC is much less than that of PID, besides, the difference between the system output and the system control input based on PID control strategy is more larger than that of ARC control system, which means that it is difficult to respond to the system control input in real time. This all indicates that the nonlinear observer can estimate the friction state well at low frequency and low speeds, and the adaptive parameter law and robust term can overcome the influence of friction compensation error and external disturbance on the system.
5. Conclusions
An adaptive robust controller is designed to compensate the frictiontorque and other nonlinear factors of the electric cylinder in this paper. The LuGre model was used to model the friction nonlinearity of the system, a nonlinear observer was designed to observe the immeasurable friction state inside the model and a parameter adaptive law was designed to estimate the uncertain parameters, besides, for parameter compensation errors and external disturbances, the linear and nonlinear robust terms were designed. The designed parameter adaptive law can approximate the unknown inertia and friction parameters to compensate the parameter uncertainty of the system, and the nonlinear observer can effectively reflect the internal friction state of the system. The linear robust term can improve the robustness and guarantee the stability of the system. The nonlinear robust term can overcome the influence of some external disturbances on the control performance of the system. The co-simulation results show that the tracking accuracy of the proposed ARC is one order of magnitude higher than that of PID, and the tracking performance and robustness of the servo system are effectively improved.
References
-
D. Liu, J. Wang, S. Wang, and D. Shi, “Active disturbance rejection control for electric cylinders with PD-type event-triggering condition,” Control Engineering Practice, Vol. 100, p. 104448, Jul. 2020, https://doi.org/10.1016/j.conengprac.2020.104448
-
H. Jian, Z. Xinhua, W. Guan, S. Zhiyi, and Y. Ting, “Adaptive friction compensation of electromechanical servo system based on LuGre model,” in 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), pp. 2596–2600, May 2018, https://doi.org/10.1109/iciea.2018.8398149
-
J. Yao, Z. Jiao, and D. Ma, “Adaptive robust control of DC motors with extended state observer,” IEEE Transactions on Industrial Electronics, Vol. 61, No. 7, pp. 3630–3637, Jul. 2014, https://doi.org/10.1109/tie.2013.2281165
-
A. Bisoffi, R. Beerens, W. P. M. H. Heemels, H. Nijmeijer, N. van de Wouw, and L. Zaccarian, “To stick or to slip: A reset PID control perspective on positioning systems with friction,” Annual Reviews in Control, Vol. 49, pp. 37–63, 2020, https://doi.org/10.1016/j.arcontrol.2020.04.010
-
F. G. Marques and C. Garcia, “Stribeck parameters estimation of a diaphragm valve using quasi newton method,” IFAC-PapersOnLine, Vol. 52, No. 1, pp. 225–230, 2019, https://doi.org/10.1016/j.ifacol.2019.06.066
-
F. Ikhouane, V. Mañosa, and G. Pujol, “Minor loops of the Dahl and LuGre models,” Applied Mathematical Modelling, Vol. 77, pp. 1679–1690, Jan. 2020, https://doi.org/10.1016/j.apm.2019.08.031
-
C. Canudas de Wit, H. Olsson, K. J. Astrom, and P. Lischinsky, “A new model for control of systems with friction,” IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419–425, Mar. 1995, https://doi.org/10.1109/9.376053
-
J. Yao, W. Deng, and Z. Jiao, “Adaptive control of hydraulic actuators with Lugre model-based friction compensation,” IEEE Transactions on Industrial Electronics, Vol. 62, No. 10, pp. 6469–6477, Oct. 2015, https://doi.org/10.1109/tie.2015.2423660
-
Bin Yao, “High performance adaptive robust control of nonlinear systems: a general framework and new schemes,” in 36th IEEE Conference on Decision and Control, pp. 2489–2494, 1997, https://doi.org/10.1109/cdc.1997.657530
