Abstract
Primary detection and removal of mechanical fault is vital for the recovery of mechanical and electrical equipment. The conventional mechanical fault recognition modules are not able obtain highly sensitive feature attributes for mechanical fault classification in the absence of prior knowledge. The fault diagnosis via data-driven methods have become a point of expansion with recent development in smart manufacturing and fault recognition techniques using the concept of deep learning. In this work, a combination of feature selection with Artificial Intelligence (AI) algorithm is presented for the mechanical fault recognition to deal with smart machine tools. This article proposes a CNN based fault recognition and classification framework that uses the combination of feature extraction, feature vector decomposition using Empirical Mode Decomposition (EMD) and deep neural network (DNN) for recognising the different fault states of the rotating machinery. The experimental outcomes obtained by the combination of EMD, feature selection module and Convolutional Neural Network (CNN) provides the detailed fault information by selecting the sensitive features from large number of faulty feature attributes. The proposed fault recognition and classification method performs better in terms of all the parameters yielding 99.01 % accuracy with respective cross-entropy loss of 0.325 and time complexity of 18 mins and 31 seconds. The comparative analysis is also done with other mainstream models and other state of the art methods, which reveals that the maximum improvement of 12.29 % is attained in terms of accuracy for the proposed fault recognition method. The presented method is robust in terms of reduction of network size, improvement of mechanical fault recognition, providing classification accuracy along with high fault diagnostic solution.
Highlights
- The proposed CNN based fault recognition and classification framework obtain the statistical feature derivatives by using the features attained from the frequency spectrum of the original signal.
- Feature vector decomposition of rotating machinery is accomplished by exploiting EMD followed by the selection of highly sensitive statistical features.
- These feature attributes are combined to recognize the different fault states of the rotating machinery using the deep neural network (DNN) and extracts the robust features from the noisy vibration samples by effectively improving the machine health information extraction.
1. Introduction
The recovery of mechanical and electrical equipment relies on the early detection and removal of faults using effectively accurate diagnosis. With the development and recent advents in smart manufacturing, the fault diagnosis via data-driven methods have become a point of development. In the current scenario, a significant improvement in the technology has been witnessed in the production of mechanical products with the recent advent of artificial intelligence (AI). The AI paradigms include machine learning (ML) and neural networks based deep learning (DL) algorithms [1, 2]. DL networks generally require a huge dataset for the computation of reliable outcomes. These methods re successful in the field of fault diagnosis in different rotating equipment yielding high classification accuracy comparative to the other machine health condition monitoring systems [3, 4].
The detection of mechanical faults has become a serious topic of concern for various industries as the mechanical faults are likely to affect the operation, thereby leading to an increased operational cost. Also, mechanical faults when happen at one component of the machinery, can trigger the chain of reactions which may damage the other components also [5-7]. The vibration signal analysis is significant for monitoring the normal and abnormal operations of the mechanical system. Multiple component failure is diagnosed using the vibration analysis which is done in time as well as frequency domain. For health state monitoring and recognition, the exert system based diagnosis is being used nowadays to solve the problems of machine diagnosis. Expert system based diagnosis have five different modules which are depicted in Figure 1.
Fig. 1Expert system based diagnosis for mechanical health state monitoring
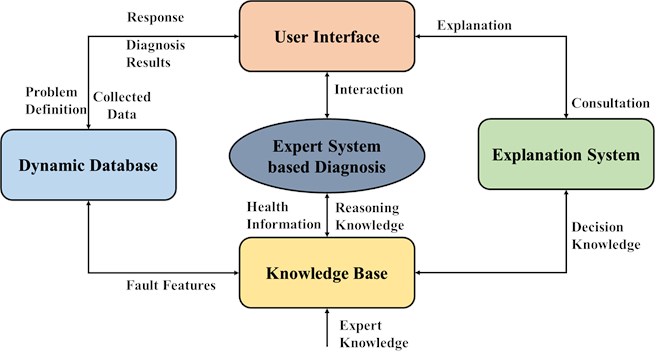
The five different modules of expert system are a dynamic dataset, knowledge base, expert monitoring the fault condition and machine health monitoring, an explanation system and a user interface [6].
Over the past few decades, for the implementation of the expert system based approaches, deep learning based Convolutional Neural Networks (CNN) have been used [7-9]. The suitability of CNN is well established for image classification and recognition, thereby, being explored for fault recognition and analysis [10, 11]. The vibration signals are periodic in nature and therefore, the data collected from such signals is not only correlated with the neighbouring data but also collected in the cycle intervals. Thus, in order to capture the fault features, these 1D signals are to be represented in 2D domain. Such analysis initially uses the 2D transformation methods, so that the signal is converted to 2D image for easy and intuitive interpretation [12]. Using the signal image, periodic features can easily be extracted using the CNN architecture, further leading to fault classification.
This work contributes in fault recognition and classification using the deep learning concept based on convolutional neural networks. The key contributions of this research are highlighted below.
– A CNN based fault recognition and classification framework is proposed in this article which uses the features attained from the frequency spectrum of the original signal to obtain the statistical feature derivatives.
– Feature vector decomposition is accomplished by exploiting EMD followed by the selection of highly sensitive features, which are combined to recognise the different fault states of the rotating machinery using the deep neural network (DNN).
– The combination of EMD and DNN extracts the robust features from the noisy vibration samples and effectively reduces the random factor effect on the machine health information extraction.
– EMD decomposes the vibration signals of the rotating machinery and extract the statistical features of the time as well as frequency domain.
The experimental outcomes obtained by the combination of EMD, feature selection module and deep learning methods provides the detailed fault information by selecting the sensitive features from large number of faulty feature attributes. The selected feature attributes are taken to the further stage for fault classification using the CNN architecture. The method presented in this article is robust in terms of reduction of network size, improvement of mechanical fault recognition, providing classification accuracy along with high fault diagnostic solution.
The rest of the article is structured as: Section 2 presents the literature review of state-of-the-art methods in the field of deep learning based mechanical fault diagnosis. Section 3 includes the material and methods followed by results and analysis in Section 4. Section 5 presents the article conclusion including the future research directions for fault analysis.
2. Literature review
In the recent years, DL has emerged as an advent in several fields like healthcare, image processing, etc. The major benefits of DL have been seen in image recognition domain [13-15]. DL can accommodate large number of feature attributes which cannot be easily processed by machine learning. Various researchers have utilized DL for fault recognition.
Qi, et al. [16] presented an ensemble empirical mode decomposition method utilizing auto regressive representation. Authors in [17] used the stacked auto encoders for fault detection and classification is done using the Softmax activation function. The fault detection accuracy computed using this method is comparatively advanced than the other current methods. Authors in [18] used the convolutional sparse encoders for the fault determination by utilizing the auto encoder signals. This approach uses the support hypothesis for flexibility improvement of the system. Some of the researchers investigated the combination of correlation with the convolutional neural networks and augmented convolutional sparse autoencoders (ACSAE) and revealed the superiorities of ACSAE for the precise detection of gear fitting faults [19]. Authors considers gears as the basic building block for damage monitoring in industrial processes. There are numerous researchers who examined the faulty conditions of gears using the data analysis method [20]. Elyassami, et al. [21] proposed a scheme for gear fault classification un order to classify wheel and pinion defects from the good gears. The temporal and spectral analysis is used for the diagnosis of gear condition. A hybrid deep belief network (DBN) system was utilized by Gai et al. [22] for the diagnosis of faulty condition using the optimization based on grasshopper algorithm. Wang et al. [23] presented a novel DBN system for the extraction of liabilities in axial piston pump. This method provides a high precision rate approving the viability and productivity of DBN for fault diagnosis.
A comparative analysis on the mechanical fault diagnosis methods utilizing DL based approaches have been detailed in Table 1 along with the technique specifications and future perspective in this field.
From this literature review, it is suggested that certain drawbacks exist in the prior research on fault diagnosis of mechanical systems using vibration signals. One of the issues lies in raw data acquisition from the sensor nodes as it difficult in the current scenario due to the existence of highly complicated systems. Therefore, there is a need for more precise and accurate sensing elements and placement of sensor nodes is also important for proper investigation of data. Besides this, most of the mechanical equipment contain the signal information that is not essential for diagnosis and leads to misinterpretation of results. Feature extraction from raw signal is a tedious task. The major limitation with the manual computation lies in its dependency on the experts having specific domain knowledge about mechanical engineering.
Therefore, in order to overcome these problems, this article proposes a combination of image processing and convolutional neural networks for enhancing the discrimination between normal and faulty condition in a mechanical system. Further, in this work, the performance comparison will be done with the several other machine learning algorithms as well as deep learning methods to rationalize the efficiency and viability of the proposed approach.
Table 1Comparative analysis of DL based methods for the diagnosis of mechanical fault
Authors | Proposed deep learning technique | Mechanical fault consideration | Future perspective |
Shao et al., 2017 [24] | Deep auto encoder feature learning | Rolling element bearing and Gear box | Other DL approached can be investigated in rotating machinery |
Verstraete et al., 2017 [25] | CNN along with Time-frequency features | Rolling element bearing | DL can be used for automation, industrial and infrastructural asset |
Gan et al., 2016 [26] | DBN and Hierarchical diagnosis network | Rolling element bearing | More features can be explored for fault diagnosis |
He and He, 2017 [27] | Large memory storage retrieval network | Bearing | Fault severity analysis can be done |
Mao et al., 2019 [28] | Multi-layer machine learning | Bearing | Deep kernel learning can be used for analysis |
Tao et al., 2016 [29] | DBN | Bearing | More faults can be analysed and compared with the existing methods |
Li et al., 2016 [30] | DBN and random forest fusion | Gear box | DBN can be improved for signal extraction |
Yao et al., 2017 [31] | kNN classifier | Rolling element bearing | Classification results can be improved using the manifold DL methods |
Zhou et al., 2018 [32] | Fusion based DL method for multimodal features | Rolling element bearing | Online early diagnosis for fault detection |
Pandarakone et al., 2018 [33] | CNN | Induction motor bearing faults | Other kind of bearing faults can be considered |
Li et al., 2018 [34] | Recurrent Neural Network | Rolling element bearing and Gear box | Reciprocating machinery can be used for analysis |
Xu et al., 2019 [35] | CNN with random forest ensemble | Bearing | Extension to other rotating devices |
3. Material and methods
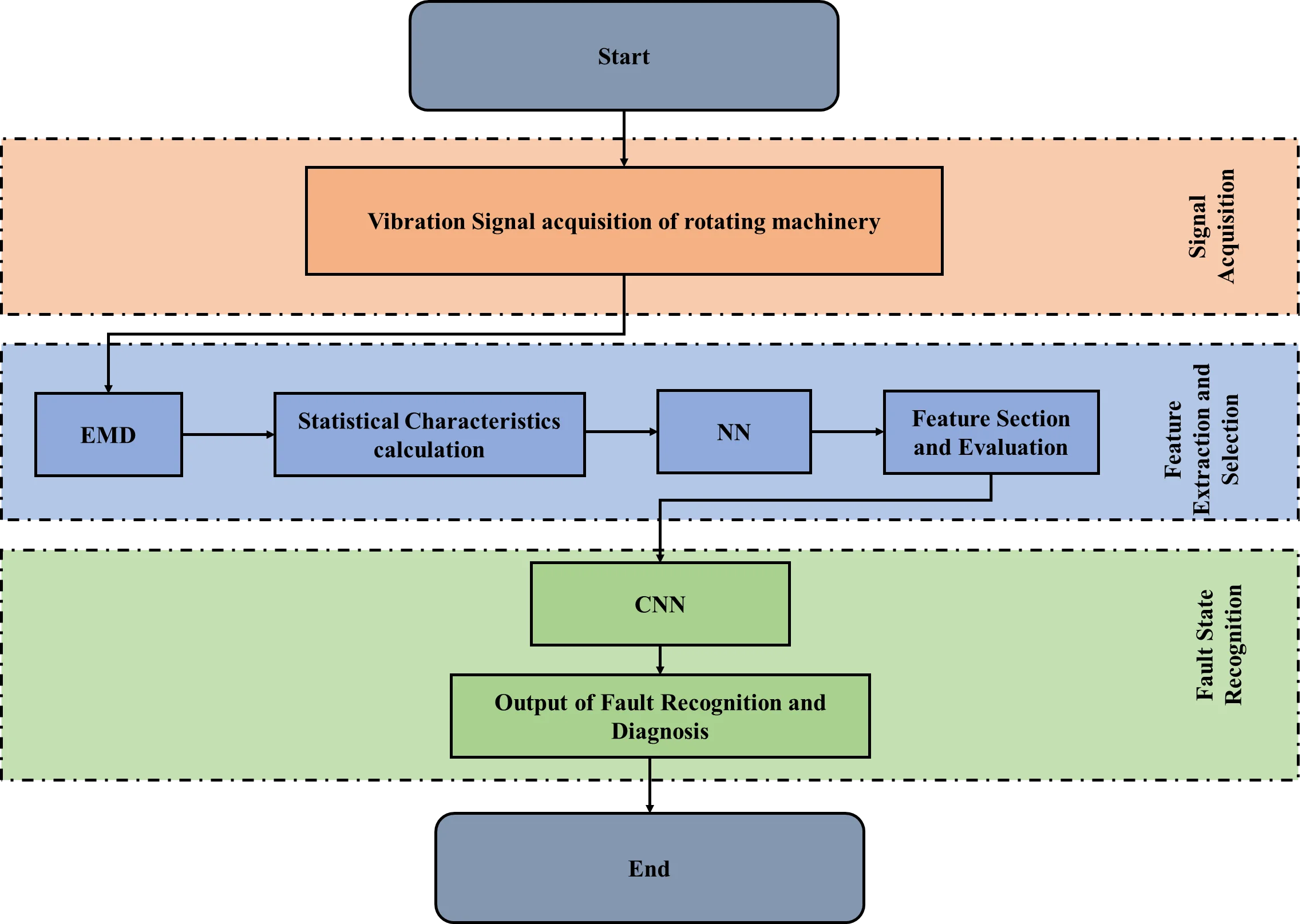
This section presents the explanation of dataset used in this work, fault feature extraction and selection, introduction of the CNN architecture and aspect of performance parameters. Fault diagnosis is a pattern recognition problem that contain various stages like signal acquisition, feature extraction and fault classification for faulty state recognition. The block diagram of the proposed fault recognition and classification system is shown in Fig. 2.
The subsequent stages of various steps involved in the proposed fault recognition and classification system are designated in the following sub-sections.
3.1. Signal acquisition and dataset description
For the acquisition of vibration signal of rotating machinery, a massive number of training samples are considered for training the CNN model sufficiently. The experimental data was attained from accelerometers situated on a mechanical system which were sampled at 12 kHz of sampling frequency. Basically, the four types of faults are considered for experimentation; ball faults, inner race faults, outer race faults and normal machinery without fault. This experiment uses 2500 1D vibration signals which are transformed into the 2D images of size 60×40. The entire dataset contains 30000 2D images for training and 7500 testing images which are used to classify the 4 faulty conditions. The details of the dataset are provided in Table 2.
Fig. 2Block diagram of the proposed Fault recognition and classification system
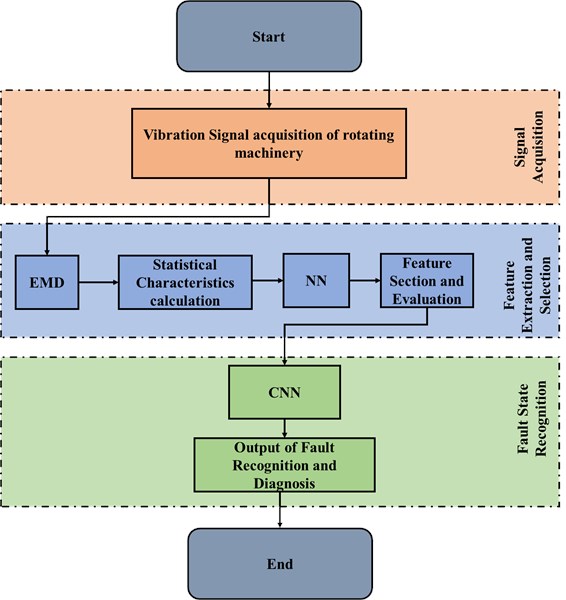
Table 2Dataset description
Faulty condition | Normal | Ball faults | Inner race faults | Outer race faults |
Training data | 3000 | 9000 | 9000 | 9000 |
Testing data | 750 | 2250 | 2250 | 2250 |
3.2. Feature extraction and selection
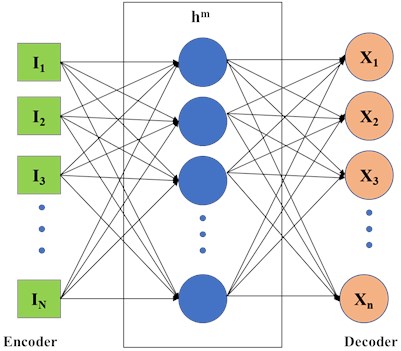
In this work the features are extracted through artificial neural network that is designed to combine the large number of training data to study the features of that particular data. This deep learning based concept does not only extracts the features but is also able to recognise the different states of fault for classification. In this work, EMD is also combined with the Neural Network (NN) architecture to determine the local characteristics of the non-stationary and non-linear signal. This combination of EMD and NN acts as a denoising encoder which extracts the relevant features from the non-linear and non-stationary signals of the rotating machinery for fault diagnosis. Fig. 3 provides the structure of the denoising encoder that is divided into two modules: encoding and decoding module.
This denoising encoder (EMD+NN) reduces the high dimensional input into a lower dimensional space and decoding module is responsible for restoring the signal in original form without noise interference. This combination of EMD and NN extracts the robust features from the noisy vibration samples and effectively reduces the influence of random factors on the machine health information extraction. Also, at the same time, EMD decomposition takes place to decompose the vibration signals of the rotating machinery and extracts the statistical characteristics of the time and frequency domain. The time domain features extracted using this technique are maximum intensity, absolute mean, peak to peak value, root mean square, kurtosis, skewness, impulse, shape and crest factors. Some of the frequency domain features extracted are centre of gravity and variance in frequency domain, etc.
Fig. 3Structure of denoising encoder and decoder (EMD+NN)
Feature selection is the dimensionality reduction step which should be carried out to obtain the optimal features out of the total features. Feature redundancy is reduces using this step and therefore it is the foremost important step which aids to the accurate faulty state classification. The algorithm used for feature selection in this work is presented in Algorithm 1.
Algorithm 1: Feature selection algorithm for faulty state recognition.
Step 1: Compute the inner distance of the features of class = using the formula expressed in Eq. (1):
where indicates the number of samples, is the number of features, number of classes are indicated by , and are the feature of samples of th class and features of the n samples of th class respectively.
Step 2: Calculate the average of the inner distance of class of feature, expressed in Eq. (2):
Step 3: Calculate the average of feature of the samples in the class , expressed in Eq. (3):
Step 4: Calculate the average of inter-distance of class of the feature using Eq. (4):
where and are the averages of features of samples in and class respectively.
Step 5: Calculate the evaluation factor for feature using Eq. (5):
Now, the features are sorted according to the value of and increase the number of features subsequently. As the number of features exhibit an increase of 5, classification accuracy does not improve and then the feature selection process is stopped. The selected features till this point are the optimal features which will be taken to the further stage for fault classification.
3.3. CNN architecture for fault classification
In this article, fault classification is accomplished using the CNN architecture. Convolutional deep neural networks are better suited for image recognition tasks and are thus implemented as part of fault diagnostics. The basic CNN model depicted in Fig. 4 consists of an input layer followed by a stack of convolutional layers, several merging layers, a fully connected layer, followed by an output layer.
Fig. 4Convolutional neural network architecture
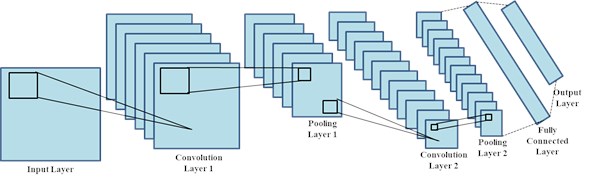
The initial network layers are responsible for the perception of edge information from the faulty images; and the further layers of the convolutional filter are accountable for finding the features which can recognise and distinguish the faulty images with different mechanical faults. The output layers provides the classification outcomes obtained by the feature information acquired at the fully connected layers.
Convolution Layer: Convolution layer is designed to accept the input and then filter kernels are used trailed by the activation function to obtain the convolution filter outputs. This layer consists of a large set of learnable convolutional filters. For an input image is the image and is the output of convolutional operation. The convolutional layer function is expressed by Eq. (6):
where is weight vector, is total number of nodes till the maximum number of node and * denotes the convolutional operator.
After the convolution operation, Rectified Linear Unit (ReLU) is used to compute the maximum of the output obtained using the function .
Pooling Layer: The convolutional layers are appended with the pooling layer after the convolution operation. This is done to obtain the down sampled output. The most used pooling operator is max pooling that computes the local maximum of input features for intermediate dimensionality reduction.
Fully connected Layer: Subsequent fully connected layers are added after the series of subsequent convolution and pooling layers to facilitate the output flattening into a single vector. This layer uses the softmax activation function for computing the output and it is expressed by Eq. (7):
where is exponential function of the output vector.
The CNN architecture used in this work for fault recognition and analysis consist of 2 convolutional layers trailed by 2 subsequent pooling layers and a fully connected layer. The parameter considerations for convolutional as well as pooling layers are tabulated in Table 3.
Table 3Parameter considerations for the CNN architecture used in the proposed system
Layer | Kernel size | Stride size | Number of filters |
Conv layer 1 | 5×5×1 | 1 | 25 |
Pool layer 1 | 2×2×1 | 2 | 25 |
Conv layer 2 | 5×5×25 | 1 | 50 |
Pool layer 2 | 2×2×1 | 2 | 50 |
3.4. Performance evaluation parameters
The presented CNN model performance is accessed for fault recognition and classification in terms of various evaluation parameter which are elaborated and formulated in this section. The parameters can be derived from true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN) are used for evaluating classification performance of NN classifier. The parameters include Accuracy (ACC), Sensitivity (SEN.), Specificity (SP.) and Precision value.
Accuracy (ACC): it defines the percentage of exactly corrected outcomes obtained out of the total number of events. The formula for ACC. is expressed by Eq. (8):
Sensitivity (SEN.): The percentage of accurately indicated faulty class cases which actually possess faulty symptoms are indicated by Sensitivity. It is also called true positive rate and is expressed by Eq. (9):
Specificity (SEP.): Specificity provides the higher probability of truly indicated non-faulty class without giving the false positive outcomes. It is expressed by Eq. (10):
Precision value: This value indicated the correctly or precisely obtained accurate results from the total number of positive predictions. Precision is expressed by Eq. (11):
Cross entropy: The cross-entropy loss is able to provide the correct classification capabilities of a neural network in the range of 0 to 1. This value should be inclined towards (0) and the expression is given in Eq. (12):
where is the number of classes, true classification is indicated by for observation , prediction probability and output is the binary indicator for precise class label classification.
4. Results and discussion
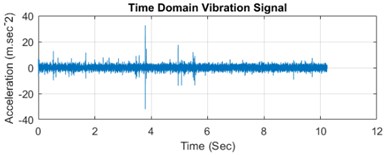
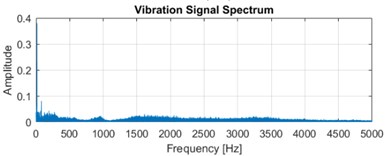
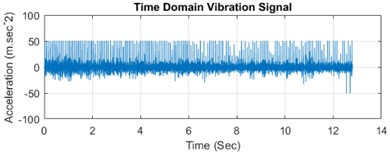
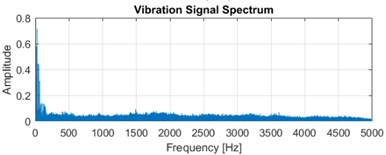
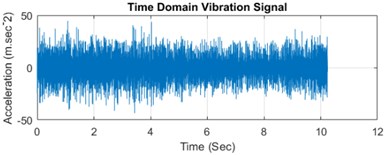
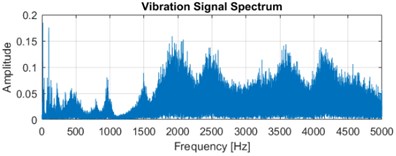
The experimentation comprises a MATLAB 2019a simulation environment equipped on a computer system with 8GB RAM, Intel processor, NVIDIA GB graphics card. The proposed work is carried out by initially using the time domain vibration signal generation and then the combination of EMD and NN is used to extract the 2D image features followed by the feature selection module. The 1D vibration signal is measured using acceleration sensor at various operating states and the time domain vibration signal as well as frequency domain signal spectrum is depicted in Fig. 5.
Fig. 5a), c), e) Represents the time domain vibration signal and b), d) and f) denotes the corresponding frequency spectrum
a)
b)
c)
d)
e)
f)
This represents the time domain vibration signals as Fig. 5(a), (c) and (e) and the corresponding frequency spectrum is indicated in Fig. 5(b), (d) and (f). The original vibration signal spectrum is decomposed utilizing the EMD method and the statistical features are extracted from the input signal. This feature extraction process using NN extracts the 96 features in total which are further reduced using the feature selection procedure. This procedure further reduces the feature dimensionality and a total of 30 relevant and optimal features are selection which can provide better average accuracy performance.
4.1. Classification results of proposed fault recognition and classification system
The classification is done using the CNN architecture and the experimentation is performed utilizing the MATLAB software. The CNN classification results are obtained in terms of various performance matrices like accuracy, sensitivity, specificity, precision, cross entropy and time complexity. The performance outcomes for fault recognition are depicted in Table 4 and are graphically presented in Fig. 6.
Table 4Performance outcomes for proposed fault recognition and classification system using CNN
Performance parameters | Values obtained |
Accuracy | 99.01 % |
Sensitivity | 99.01 % |
Specificity | 99.00 % |
Precision | 99.50 % |
Cross entropy loss | 0.325 |
Time complexity | 18 mins 31 secs |
Fig. 6Visual representation of performance parameters obtained for proposed system
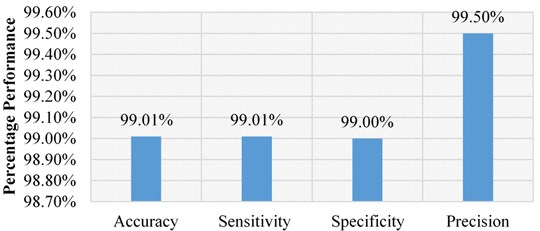
Both tabular and visual representation depicts that the favourable outcomes are achieved for the proposed fault recognition and classification system. The method achieves the performance parameters as; 99.01 % accuracy, 99.01 % sensitivity, 99.00 % specificity and 99.50 % precision value. The cross-entropy loss and time complexity are used as cost analysis parameters for the proposed framework, which should be minimized for the reliable network. The cross-entropy value of 0.325 and time complexity of 18 mins and 31 seconds is seen for the proposed fault recognition method.
4.2. Comparison with different main-stream CNN models
There are various main-stream pre-trained CNN architectures which are used by various researchers for fault and image recognition purpose. A comparative analysis of the proposed framework is done with the existing main-stream CNN models like AlexNet [36], GoogleNet [37], ResNet [38] and VggNet [39] in terms of network accuracy performance, and time complexity. The comparison is drawn in Fig. 7.
Fig. 7Comparative analysis of proposed fault recognition system with other mainstream models
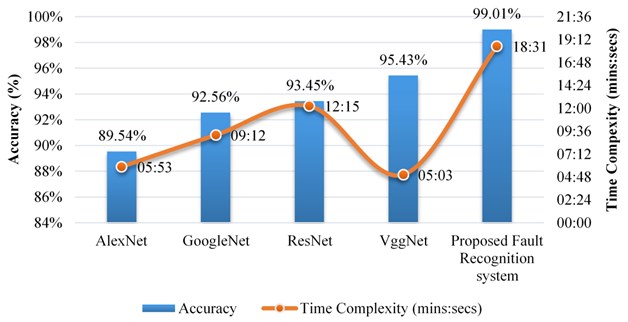
This graphical analysis reveals that the proposed fault recognition system provides the most significant outcomes among all the pre-trained mainstream CNN models. The performance through network parameters is maximum for the proposed fault recognition framework. However, while comparing the time complexity, the proposed framework maintains a trade-off in this case and is a bit complex comparative to the other mainstream models.
4.3. Comparison with the state-of-the-art methods
In this work, a comparison is also done with the other state-of-the-art methods reported in the literature for fault recognition and classification employing the CNN based methodology. This comparison is drawn in Table 5.
Table 5Comparison of existing state-of-the-art methods with the proposed system
Method used | Sensitivity | Specificity | Precision | Accuracy | Percentage improvement in terms of accuracy |
Shao et al., 2017 [24] | 96.62 % | 91.59 % | 91.74 % | 94.05 % | 5.27 % |
Tao et al., 2016 [29] | 96.62 % | 98.00 % | 98.04 % | 97.50 % | 1.54 % |
Zhou et al., 2018 [32] | 94.34 % | 91.59 % | 91.74 % | 93.06 % | 6.39 % |
Pandarakone et al., 2018 [33] | 90.09 % | 87.50 % | 87.72 % | 88.17 % | 12.29 % |
Li et al., 2018 [34] | 95.24 % | 96.08 % | 96.15 % | 95.90 % | 3.24 % |
Proposed system | 99.01 % | 99.00 % | 99.50 % | 99.01 % | Selected |
The comparison reveals that the proposed model outperforms the other state of the art methods in terms of all the performance parameters thereby, shows its competence for faulty state classification. A reliable fault recognition and classification solution is achieved using the proposed framework.
5. Conclusions
This article proposes a CNN based fault recognition and classification framework that uses the feature extraction process exploiting EMD followed by the selection of highly sensitive features which are combined to recognise the different fault states of the rotating machinery using the DNN. The experimental outcomes obtained by combining the EMD, feature selection and CNN provides the detailed fault information for further fault classification. The method achieves a good quality performance in terms of all the parameters yielding 99.01 % accuracy with respective cross-entropy loss of 0.325 and time complexity of 18 mins and 31 seconds. The comparative analysis is also done with other mainstream models by considering the network performance accuracy and time complexity, which reveals the trade-off among the two parameters. The performance validation with the other existing methods reveals that the maximum accuracy improvement of 12.29 % is achieved for the proposed fault recognition framework. The proposed fault recognition method is robust in terms of reduction of network size, improvement of mechanical fault recognition and provides high classification accuracy along with a viable fault diagnostic solution. Using the proposed approach for real time fault recognition classification scenario will be the key emphasis of research in the future perspective of this work.
References
-
Wason R. Deep learning: Evolution and expansion. Cognitive Systems Research, Vol. 52, 2018, p. 701-708.
-
Palaz D., Collobert R., Doss M. M. Estimating phoneme class conditional probabilities from raw speech signal using convolutional neural networks. arXiv preprint arXiv:1304.1018, 2013.
-
Gerek O. N., Ece D. G. 2-D analysis and compression of power-quality event data. IEEE Transactions on Power Delivery, Vol. 19, Issue 2, 2004, p. 791-798.
-
Dhiman G., Oliva D., Kaur A., Singh K. K., Vimal S., Sharma A., Cengiz K. BEPO: A novel binary emperor penguin optimizer for automatic feature selection. Knowledge-Based Systems, Vol. 211, 2021, p. 106560.
-
Dhiman G., Singh K. K., Soni M., Nagar A., Dehghani M., Slowik A., et al. MOSOA: a new multi-objective seagull optimization algorithm. Expert Systems with Applications, Vol. 167, 2021, p. 114150.
-
Wong P. K., Zhong J., Yang Z., Vong C. M. Sparse Bayesian extreme learning committee machine for engine simultaneous fault diagnosis. Neurocomputing, Vol. 174, 2016, p. 331-343.
-
Poongodi M., Sharma A., Vijayakumar V., Bhardwaj V., Sharma A. P., Iqbal R., Kumar R. Prediction of the price of Ethereum blockchain cryptocurrency in an industrial finance system. Computers and Electrical Engineering, Vol. 81, 2020, p. 106527.
-
Bhardwaj C., Jain S., Sood M. Diabetic retinopathy severity grading employing quadrant‐based Inception‐V3 convolution neural network architecture. International Journal of Imaging Systems and Technology, Vol. 31, Issue 2, 2021, p. 592-608.
-
Rathee G., Sharma A., Kumar R., Ahmad F., Iqbal R. A trust management scheme to secure mobile information centric networks. Computer Communications, Vol. 151, 2020, p. 66-75.
-
Bhardwaj C., Jain S., Sood M. Deep learning based diabetic retinopathy prediction of colored fundus images with parameter tuning. Advances in Computational Intelligence Techniques, 2020, p. 53-62.
-
Yuvaraj N., Srihari K., Dhiman G., Somasundaram K., Sharma A., Rajeskannan S., et al. Nature-inspired-based approach for automated cyberbullying classification on multimedia social networking. Mathematical Problems in Engineering, Vol. 2021, 2021, p. 6644652.
-
Bhardwaj C., Jain S., Sood M. Hierarchical severity grade classification of non-proliferative diabetic retinopathy. Journal of Ambient Intelligence and Humanized Computing, Vol. 12, 2021, p. 2649-2670.
-
Manikandan S., Duraivelu K. Fault diagnosis of various rotating equipment using machine learning approaches – a review. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, Vol. 235, Issue 2, 2020, p. 629-642.
-
Han D., Liang K., Shi P. Intelligent fault diagnosis of rotating machinery based on deep learning with feature selection. Journal of Low Frequency Noise, Vibration and Active Control, Vol. 39, Issue 4, 2020, p. 939-953.
-
Li X., Jiang H., Hu Y., Xiong X. Intelligent Fault Diagnosis of Rotating Machinery Based on Deep Recurrent Neural Network. International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), 2018, p. 67-72.
-
Qi Y., Shen C., Wang D., Shi J., Jiang X., Zhu Z. Stacked sparse autoencoder-based deep network for fault diagnosis of rotating machinery. IEEE Access, Vol. 5, 2017, p. 15066-15079.
-
Li J., Li X., He D., Qu Y. A novel method for early gear pitting fault diagnosis using stacked SAE and GBRBM. Sensors, Vol. 19, Issue 4, 2019, p. 758.
-
Li X., Li J., He D., Qu Y. Gear pitting fault diagnosis using raw acoustic emission signal based on deep learning. Eksploatacja i Niezawodność, Vol. 21, Issue 3, 2019, p. 403-410.
-
Kane P. V., Andhare A. B. End of the assembly line gearbox fault inspection using artificial neural network and support vector machines. International Journal of Acoustics and Vibration, Vol. 24, Issue 1, 2019, p. 68-84.
-
Li X., Li J., Qu Y., He D. Gear pitting fault diagnosis using integrated CNN and GRU network with both vibration and acoustic emission signals. Applied Sciences, Vol. 9, Issue 4, 2019, p. 768.
-
Elyassami Y., Benjelloun K., Er Rajouany M. Gear fault diagnosis and classification using data vibration. Journal of Engineering and Applied Sciences, Vol. 12, 2017, p. 5617-5625.
-
Gai J., Shen J., Wang H., Hu Y. A parameter-optimized DBN using GOA and its application in fault diagnosis of gearbox. Shock and Vibration, Vol. 2020, 2020, p. 429409.
-
Wang S., Xiang J., Zhong Y., Tang H. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mechanical Systems and Signal Processing, Vol. 112, 2018, p. 154-170.
-
Shao H., Jiang H., Zhao H., Wang F. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis. Mechanical Systems and Signal Processing, Vol. 95, 2017, p. 187-204.
-
Verstraete D., Ferrada A., Droguett E. L., Meruane V., Modarres M. Deep learning enabled fault diagnosis using time-frequency image analysis of rolling element bearings. Shock and Vibration, Vol. 2017, 2017, p. 5067651.
-
Gan M., Wang C. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings. Mechanical Systems and Signal Processing, Vol. 72, 2016, p. 92-104.
-
He M., He D. Deep learning based approach for bearing fault diagnosis. IEEE Transactions on Industry Applications, Vol. 53, Issue 3, 2017, p. 3057-3065.
-
Mao W., Feng W., Liang X. A novel deep output kernel learning method for bearing fault structural diagnosis. Mechanical Systems and Signal Processing, Vol. 117, 2019, p. 293-318.
-
Tao J., Liu Y., Yang D. Bearing fault diagnosis based on deep belief network and multisensor information fusion. Shock and Vibration, Vol. 2016, 2016, p. 9306205.
-
Li C., Sanchez R. V., Zurita G., Cerrada M., Cabrera D., Vásquez R. E. Gearbox fault diagnosis based on deep random forest fusion of acoustic and vibratory signals. Mechanical Systems and Signal Processing, Vol. 76, 2016, p. 283-293.
-
Yao B., Zhen P., Wu L., Guan Y. Rolling element bearing fault diagnosis using improved manifold learning. IEEE Access, Vol. 5, 2017, p. 6027-6035.
-
Zhou F., Hu P., Yang S., Wen C. A multimodal feature fusion-based deep learning method for online fault diagnosis of rotating machinery. Sensors, Vol. 18, Issue 10, 2018, p. 3521.
-
Pandarakone S. E., Masuko M., Mizuno Y., Nakamura H. Deep neural network based bearing fault diagnosis of induction motor using fast Fourier transform analysis. IEEE Energy Conversion Congress and Exposition (ECCE), 2018, p. 3214-3221.
-
Li H., Zhao J., Ni X., Zhang X. Fault diagnosis for machinery based on feature extraction and general regression neural network. International Journal of System Assurance Engineering and Management, Vol. 9, Issue 5, 2018, p. 1034-1046.
-
Xu G., Liu M., Jiang Z., Söffker D., Shen W. Bearing fault diagnosis method based on deep convolutional neural network and random forest ensemble learning. Sensors, Vol. 19, Issue 5, 2019, p. 1088.
-
Krizhevsky A., Sutskever I., Hinton G. E. Imagenet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems, Vol. 25, 2012, p. 1097-1105.
-
Szegedy C., Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., et al. Going deeper with convolutions. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015.
-
He K., Zhang X., Ren S., Sun J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016.
-
Simonyan K., Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.
About this article
Scientific research and technological guidance project of colleges and universities in Hebei Province in 2020 (Z2020232), General project supported by the team of Tangshan Normal University in 2020 (2020C13), Science and technology research youth fund project of colleges and universities in Hebei Province in 2020 (QN2020513), The Research Fund Project of Tangshan Normal University in 2021 (2021B29).
