Abstract
A model having two degrees of freedom and incorporating a specific type of nonlinearity is proposed for the analysis of dynamics of a pipe robot. Specific type of nonlinearity has different values of viscous friction depending on the sign of velocity of the system. Numerical investigations for various parameters of the system are presented. Optimal frequency of excitation of a pipe robot is determined. The obtained results are used in the process of design of pipe robots: it is especially important to choose the frequency of excitation in order to ensure effective operation of a pipe robot.
1. Introduction
Resonances in nonlinear systems play an important role in dynamics of different mechanisms [1]. Impacts and dynamics of systems for various types of excitations are investigated in [2]. Stabilisation of nonlinear systems is analysed in [3]. Dynamical systems with impacts are investigated in [4]. Periodic orbits in mechanical systems are described in [5]. Vibro-impact energy sink and its nonlinear qualities are analysed in [6]. Dynamics of particle interacting with a wall is investigated in [7]. Frequencies of a multibody dynamical system are analysed in [8]. Mechanism of a specific type having a pendulum is investigated in [9]. Piecewise linearity in a model of a dynamical system is analysed in [10]. Resonant zones of a nonlinear vibrating system are investigated in [11]. Sommerfeld effect in a nonlinear dynamical system is analysed in [12]. Isolated resonances of a vibrating system are investigated in [13]. Robot travelling inside the pipe is described in [14]. Review of modeling of pipe robots is presented in [15]. Pipe inspection robot is developed and investigated in [16]. Pipe leak detection robot is analysed in [17]. Method of design of a pipe robot is described in [18]. Modeling and control of a pipe inspection robot is investigated in [19]. Design of pipe inspection robots is developed in [20]. Mechanisms of pipe robots that inspect various pipe types are investigated in [21].
A model comprising two degrees of freedom and incorporating a specific type of nonlinearity is proposed for the analysis of dynamics of a pipe robot. Specific type of nonlinearity has different values of viscous friction depending on the sign of velocity of the system. Numerical investigations for various parameters of the system are presented. Optimal frequency of excitation of a pipe robot is determined. The obtained results are used in the process of design of pipe robots.
The major objective of this paper is to propose the model of a pipe robot. The motions of a pipe robot on the basis of a proposed model are investigated and graphical relationships are obtained. They enable to choose desirable parameters of a pipe robot.
2. A phenomenological model of a pipe robot
The governing equations of the model of a pipe robot read:
where and are non dimensional displacements of the first and second degrees of freedom of the investigated system, is the non dimensional coefficient of viscous damping between the two interacting elements of the investigated system, is the non dimensional amplitude of the exciting force, is the non dimensional frequency of the exciting force, is the non dimensional time variable, is the non dimensional mass of the system, and are non dimensional coefficients of viscous friction and denotes differentiation with respect to the non dimensional time.
3. The dynamics of the system – computational experiments
The following values of the parameters of the system were assumed in the investigation:
Investigations were performed for three values of non dimensional frequency of excitation:
as well as for two values of non dimensional coefficient of viscous friction :
Two periods of steady state motion are investigated. This enables to visually estimate if the steady state regime has been reached.
3.1. The dynamics of the system at
Graphical results of investigation of dynamics of the system at are presented in Fig. 1.
Fig. 1Dynamics of the system for the first value of h2 (the first degree of freedom represented by continuous lines and the second degree of freedom represented by dashed lines)
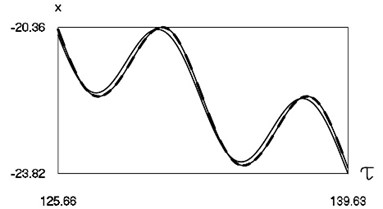
a) Non dimensional displacements as functions of non dimensional time
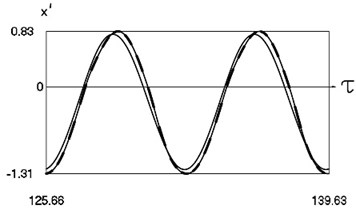
b) Non dimensional velocities as functions of non dimensional time
Graphical results of investigation of dynamics of the system at are presented in Fig. 2.
Fig. 2Dynamics of the system for the second value of h2 (the first degree of freedom represented by continuous lines and the second degree of freedom represented by dashed lines)
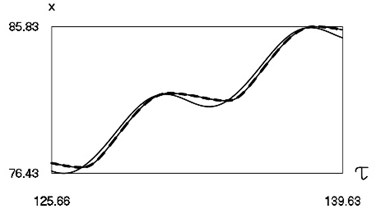
a) Non dimensional displacements as functions of non dimensional time
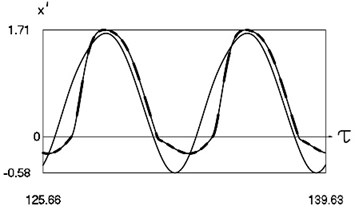
b) Non dimensional velocities as functions of non dimensional time
3.2. The dynamics of the system at
Graphical results of investigation of dynamics of the system at are presented in Fig. 3.
Fig. 3Dynamics of the system for the first value of h2 (the first degree of freedom represented by continuous lines and the second degree of freedom represented by dashed lines)
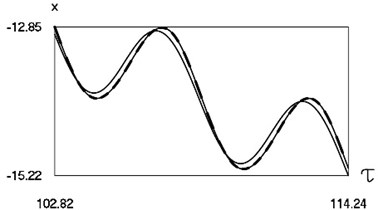
a) Non dimensional displacements as functions of non dimensional time
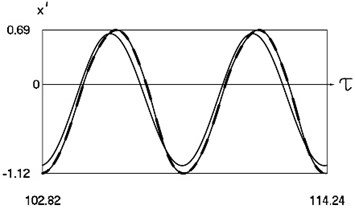
b) Non dimensional velocities as functions of non dimensional time
Graphical results of investigation of dynamics of the system at are presented in Fig. 4.
Fig. 4Dynamics of the system for the second value of h2 (the first degree of freedom represented by continuous lines and the second degree of freedom represented by dashed lines)
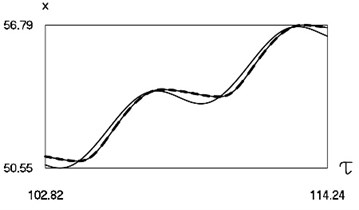
a) Non dimensional displacements as functions of non dimensional time
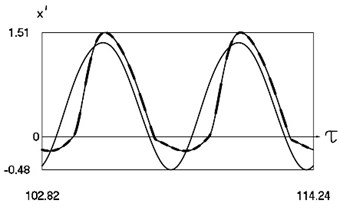
b) Non dimensional velocities as functions of non dimensional time
3.3. The dynamics of the system at
Graphical results of investigation of dynamics of the system at are presented in Fig. 5.
Graphical results of investigation of dynamics of the system at are presented in Fig. 6.
Fig. 5Dynamics of the system for the first value of h2 (the first degree of freedom represented by continuous lines and the second degree of freedom represented by dashed lines)
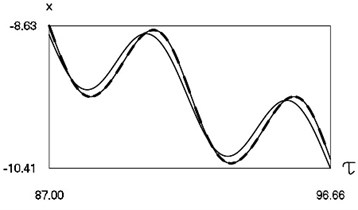
a) Non dimensional displacements as functions of non dimensional time
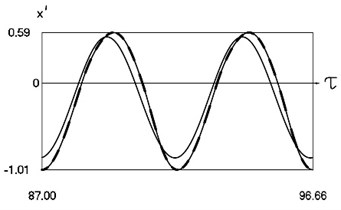
b) Non dimensional velocities as functions of non dimensional time
Fig. 6Dynamics of the system for the second value of h2 (the first degree of freedom represented by continuous lines and the second degree of freedom represented by dashed lines)
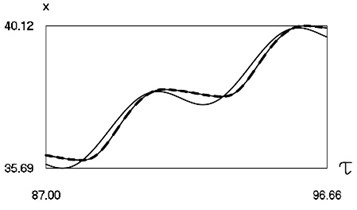
a) Non dimensional displacements as functions of non dimensional time
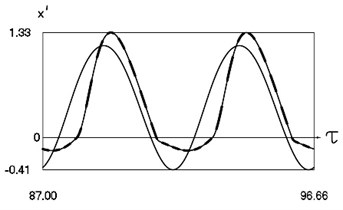
b) Non dimensional velocities as functions of non dimensional time
From the presented graphical results one can note that for the first value of the non dimensional coefficient of viscous friction motion of the pipe robot takes place in the negative direction, while for the second value of the non dimensional coefficient of viscous friction motion of the pipe robot takes place in the positive direction. From the presented results it can be seen that variation of velocity in steady state regime is periodic. Dependence of the obtained results from the frequency of excitation is observed in the obtained graphical relationships.
4. Investigation of non dimensional average velocity as function of viscous friction
The following values of the parameters of the system were assumed in the investigation:
Investigations were performed for four values of non dimensional frequency of excitation:
Non dimensional coefficient of viscous friction was assumed to be in the interval:
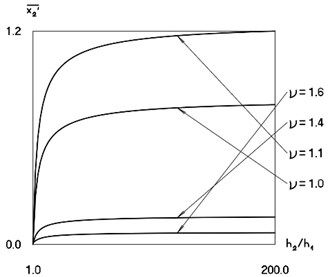
Non dimensional average velocity as function of viscous friction is represented in Fig. 7.
The presented graphical relationships enable to determine the value of non dimensional viscous friction which can be used in the model of the pipe robot for investigations of its dynamics.
Fig. 7Non dimensional average velocity of the system as function of viscous friction
5. Determination of optimal non dimensional frequency of excitation
The following values of the parameters of the system were assumed in the investigation:
Non dimensional frequency of excitation was assumed to be in the interval:
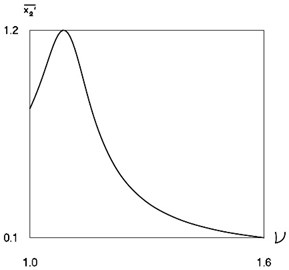
Non dimensional average velocity as function of non dimensional frequency of excitation is represented in Fig. 8.
Fig. 8Non dimensional average velocity of the system as function of non dimensional frequency of excitation
It can be noted that the values of 0.1, 20 were chosen on the basis of the results presented in Fig. 7. Large value of non dimensional coefficient of viscous friction enables to represent the behaviour of the self – stopping mechanism.
The presented graphical relationship determines optimal non dimensional frequency of excitation which corresponds to maximum non dimensional average velocity of the system: it is especially important to choose the frequency of excitation in order to ensure effective operation of a pipe robot.
6. Conclusions
In this paper a model having two degrees of freedom and incorporating a specific type of nonlinearity is proposed for the analysis of dynamics of a pipe robot. Numerical investigations for various parameters of the system are presented and graphical relationships are obtained. They enable to choose desirable parameters of a pipe robot.
The presented graphical relationship of non-dimensional average velocity as function of viscous friction enables to determine the value of non-dimensional viscous friction which can be used in the model of the pipe robot for investigations of its dynamics.
The presented graphical relationship of non-dimensional average velocity of the system as function of non-dimensional frequency of excitation determines optimal non dimensional frequency of excitation which corresponds to maximum non dimensional average velocity of the investigated system. Thus, optimal frequency of excitation of a pipe robot is determined.
The obtained results are used in the process of design of pipe robots. In practical applications it is especially important to choose the frequency of excitation in order to ensure effective operation of a pipe robot.
References
-
Wedig W. V. New resonances and velocity jumps in nonlinear road-vehicle dynamics. Procedia IUTAM, Vol. 19, 2016, p. 209-218.
-
Li T., Gourc E., Seguy S., Berlioz A. Dynamics of two vibro-impact nonlinear energy sinks in parallel under periodic and transient excitations. International Journal of Non-Linear Mechanics, Vol. 90, 2017, p. 100-110.
-
Zaitsev V. A. Global asymptotic stabilization of periodic nonlinear systems with stable free dynamics. Systems and Control Letters, Vol. 91, 2016, p. 7-13.
-
Dankowicz H., Fotsch E. On the analysis of chatter in mechanical systems with impacts. Procedia IUTAM, Vol. 20, 2017, p. 18-25.
-
Spedicato S., Notarstefano G. An optimal control approach to the design of periodic orbits for mechanical systems with impacts. Nonlinear Analysis: Hybrid Systems, Vol. 23, 2017, p. 111-121.
-
Li W., Wierschem N. E., Li X., Yang T. On the energy transfer mechanism of the single-sided vibro-impact nonlinear energy sink. Journal of Sound and Vibration, Vol. 437, 2018, p. 166-179.
-
Marshall J. S. Modeling and sensitivity analysis of particle impact with a wall with integrated damping mechanisms. Powder Technology, Vol. 339, 2018, p. 17-24.
-
Salahshoor E., Ebrahimi S., Zhang Y. Frequency analysis of a typical planar flexible multibody system with joint clearances. Mechanism and Machine Theory, Vol. 126, 2018, p. 429-456.
-
Starossek U. Forced response of low-frequency pendulum mechanism. Mechanism and Machine Theory, Vol. 99, 2016, p. 207-216.
-
Wang S., Hua L., Yang C., Zhang Y., Tan X. Nonlinear vibrations of a piecewise-linear quarter-car truck model by incremental harmonic balance method. Nonlinear Dynamics, Vol. 92, 2018, p. 1719-1732.
-
Alevras P., Theodossiades S., Rahnejat H. On the dynamics of a nonlinear energy harvester with multiple resonant zones. Nonlinear Dynamics, Vol. 92, 2018, p. 1271-1286.
-
Sinha A., Bharti S. K., Samantaray A. K., Chakraborty G., Bhattacharyya R. Sommerfeld effect in an oscillator with a reciprocating mass. Nonlinear Dynamics, Vol. 93, 2018, p. 1719-1739.
-
Habib G., Cirillo G. I., Kerschen G. Isolated resonances and nonlinear damping. Nonlinear Dynamics, Vol. 93, 2018, p. 979-994.
-
Yeh C.-Y., Chen C.-Y., Juang J.-Y. Soft hopping and crawling robot for in-pipe traveling. Extreme Mechanics Letters, Vol. 39, 2020, p. 100854.
-
Rashid M. Z. A., Yakub M. F. M., Salim S. A. Z. B. S., Mamat N., Putra S. M. S. M., Roslan S. A. Modeling of the in-pipe inspection robot: a comprehensive review. Ocean Engineering, Vol. 203, 2020, p. 107206.
-
Bhadoriya A. V. S., Gupta V. K., Mukherjee S. Development of in-pipe inspection robot. Materials Today, Vol. 5, Issue 9, 2018, p. 20769-20776.
-
Uyanik C., Erdemir E., Kaplanoglu E., Sekmen A. A deep learning approach for motion segment estimation for pipe leak detection robot. Procedia Computer Science, Vol. 158, 2019, p. 37-44.
-
Qiao J., Shang J. Application of axiomatic design method in in-pipe robot design. Robotics and Computer-Integrated Manufacturing, Vol. 29, Issue 4, 2013, p. 49-57.
-
Ciszewski M., Buratowski T., Giergiel M. Modeling, simulation and control of a pipe inspection mobile robot with an active adaptation system. IFAC – Papers on Line, Vol. 51, Issue 22, 2018, p. 132-137.
-
Ibrahimov B. Development of a decision making guide for locomotion design for in-pipe inspection robots – one step towards open innovation in robotics. IFAC – Papers on Line, Vol. 49, Issue 29, 2016, p. 77-82.
-
Lee D., Park J., Hyun D., Yook G. H., Yang H.-S. Novel mechanisms and simple locomotion strategies for an in-pipe robot that can inspect various pipe types. Mechanism and Machine Theory, Vol. 56, 2012, p. 52-68.
