Abstract
The arrangement optimization algorithm of blades can reduce the vibration localization of mistuned bladed disk in a compressor of aero-engine, however, it will destroy the dynamic balance of bladed disk. A new arrangement optimization method of isolation zone on bladed disk system considering unbalance moment is proposed, on the basis the reduced order modeling technology. This method is based on the finite element model and can be implemented as fast and accurate vibration reduction optimization without destroying the mass balance of the bladed disk system, the method considers both mass and stiffness mistuning. Firstly, the discrete particle swarm optimization algorithm is used to sort the mass-mistuned blades according to unbalanced moment, then, the arranged bladed disk is divided into 6 isolation zones, then, in each isolation zone, the stiffness mistuned bladed disk is arranged optimally by the stiffness mistuning optimization algorithm. Under the premise of satisfying the dynamic balance of bladed disk, this algorithm optimizes the arrangement of blades with mass mistuning and stiffness mistuning, and achieves the purpose of vibration reduction optimization of mistuned bladed disk. The results show that, the maximum amplitude of the bladed disk system is reduced by 23.9 %. The vibration localization degree of the optimized blade are reduced by 46.3 %.
Highlights
- A new arrangement optimization method of isolation zone on bladed disk system considering unbalance moment is proposed.
- The method is based on the finite element model and can be implemented as fast and accurate vibration reduction optimization without destroying the mass balance of the bladed disk system.
- The method considers both mass and stiffness mistuning.
1. Introduction
Mistuning is a common phenomenon in the bladed disk system of aero-engine compressor, mistuning is also the inconsistency of the blade mass, stiffness and frequency due to material, manufacture and wear. Mistuning increases the vibration amplitude of a few blades, and aggravates the vibration of the bladed disk system, resulting in severe vibration localization. It is found that by adjusting the installation position of blades it is possible to reduce the vibration amplitude of the mistuned bladed disk system [1, 2].
Because of mistuning, the cyclic symmetry of the bladed disk system is destroyed and the circular symmetry structure cannot be analyzed. If the finite element model is adopted for the blisk, it will be difficult to calculate accurately the tuning parameters. Due to the advantages of the finite element reduced order modeling technique, it is widely applied in solving large scale dynamic calculation problems. The finite element reduced order modeling technique is based on the substructure component mode synthesis method, which can greatly reduce the degree of freedom of the dynamic model on the premise of satisfying the requirements of the engineering accuracy. The substructure component mode synthesis method can be divided into three categories: the fixed interface method [3-5], free interface method [6-8] and mixed method [9-11].
For the studies of the vibration reduction optimization algorithm for the mistuned bladed disk system, some experts and scholars proposed a lot of improved algorithms in recent years. Fu [12] proposed an algorithm for blade sorting based on that for rotor blades for turbo-machinery. By adopting this algorithm, the smaller resultant moments can be obtained by interchanging the left and right positions of some blades and the upper and lower positions. In view of the unbalance problem caused by the mass mistuning of the bladed disk, the genetic algorithm is used to study the optimization of the mass-mistuned blade and to compare it with the exhaustion method. The results show that the genetic algorithm and the simulated annealing method have the advantages of short time and fast convergence speed [13]. Genetic algorithm is used to sort and optimize the unbalance between blades caused by mass and inertia [14]. Tang [15] divided 24 blades into 6 quadrants. The genetic algorithm is used to make the optimal target for the minimum difference of the total blade mass and the maximum frequency difference between adjacent blade. Jia [16] used a genetic algorithm to consider the initial unbalances and blade mass moments, and to verify the correctness of the method by analyzing the blade installation of a compressor.
Choi [17-19] aimed at solving the problem of blade weight balance, adopted an intentional mistuned bladed disk to reduce the sensitivity of random mistuning, limit the number of different blades and use a heuristic algorithm to study the order of blades. Thompson and Becus [20] studied the optimal sorting problem of the mistuned blade, and restricted the blade to the mistuning of the torsion stiffness in a small range, and used the simulated annealing algorithm to solve the blade position. Bisegna [21] studied the optimization problem of the innovative passive vibration damping system that requires sophisticated models [22-24] and consists of blades installed on equidistant flexible rings. The blades are equipped with piezoelectric devices to convert the vibration energy into electrical energy, and the electrical energy is dissipated through an electrical shunt which contains resistance elements. Hohl [25] proposed a method to reduce the degree of localization of mistuned disks. This method can allow finding the pattern of blade arrangement which is insensitive to energy localization. Monte Carlo simulation is carried out by the reduced order model, and the influence law of the variance of the mistuned blades is discussed. This rule can restrain the localization of energy. Yuan [26, 27] adopted the intelligent optimization algorithm to optimize the blade installation sequence according to the vibration localization problem of the bladed disk system. Li and Deng [28-30] suppress the vibration localization of the mistuned bladed disk structure based on the piezoelectric network and the lumped parameter model of the cycle period. The effect of mistuning of mechanical and electrical systems on the forced response of the disks was studied. The effect of the piezoelectric network was evaluated by adopted MMAC (the modified modal assurance criterion). Deng [31] took the minimum walking distance of passengers, the minimum variance of free time for each door, the minimum number of flights on the apron and the most reasonable utilization rate of the door as the optimization objective, and proposed an effective multi-objective door allocation optimization model. Then, based on the advantages of α stable distribution and dynamic fractional calculus, he studied an improved adaptive particle swarm optimization (DOADAPO) algorithm. In order to balance the convergence speed and solution diversity, and Deng [32] improved the optimization performance in solving the large-scale optimization problem, by proposing an improved ant colony optimization (ICMPACO) algorithm based on the multi-population strategy, co-evolution mechanism, pheromone updating strategy, and pheromone diffusion mechanism.
Based on the above-mentioned studies on the vibration reduction optimization for a mistuned bladed disk, most scholars adopt a lumped parameter model; however, the lumped parameter model and finite element model have some deviations in the calculation results. Some scholars did not consider the condition of mistuning for both the mass and stiffness comprehensively. The dynamic results of the finite element model of the bladed disk system are more convincing, on the basis of this model, under the premise of keeping the minimum unbalance moment of bladed disk system, considering the mass and stiffness mismatch, it is significant to use an intelligent optimization algorithm to study the vibration reduction optimization of mistuned bladed disk system.
In the summary based on the reduced order model Method described in Ref. [33], this study mainly focuses on the vibration reduction optimization for blades affected by mistuning which are not involved in Ref. [33]. Moreover, besides the pre-stressed condition shown in Ref. [33], the coriolis force also influences the bladed disk system dynamic model. Besides the mistuning of blades stiffness as in Ref. [33], an intelligent optimization algorithm is adopted to optimize the arrangement of mistuned blades in terms of both mass and stiffness. Firstly, the particle swarm optimization algorithm is adopted to optimize the mass mistuned blades, and the best optimized arrangement scheme is divided into six isolation zones, secondly, the arrangement optimization of the location of stiffness mistuned blades in each isolation zone. Finally, the optimal arrangement of the mistuned bladed disk system is obtained under the condition that the unbalance moment of the bladed disk system and the vibration localization degree are minimal.
2. Dynamic reduced order models
An aeroengine compressor bladed disk system consists of 38 blades and disks connected by mortise and tenon structure. If the finite element model of blisk structure is adopted, the number of elements will be huge, and the nonlinear contact state of mortise and tenon will be considered, that will lead to calculation problems. For large complex rotor systems, the cyclic symmetry structure is often used; however, the mistuning destroys the cyclic symmetry of the bladed disk structure, so the cyclic symmetry analysis method cannot be used.
The reduced order modeling technique provides a method to solve the dynamic problems of mistuned bladed disk system. The reduced order models for a bladed disk of an aero-engine compressor were established by adopting the reduced order modeling technique according to the installation angle of the blade; the blade and the corresponding disk are taken as a substructure model, and the whole bladed disk system is divided into 38 substructure models. The cutting surface of the disk in each substructure is taken as the interface, the nodes on the interface are selected to define the master degree of freedom, and the nodes on the non-interface are taken as the slave degrees of freedom.
The bladed disk dynamic reduced order models considering the coriolis force was adopted. The blisk and substructure model of the bladed disk is shown in Fig. 1.
Fig. 1Blisk and substructure model of bladed disk

The aero-engine’ compressor blades under the centrifugal force, the natural frequency and dynamic response of the structure will be affected, considering the influence of the rotor system’s centrifugal stiffening effect on the dynamic characteristics, and the equation can be expressed as:
where, , , , , , , , and are mass matrix, damping matrix, Coriolis force matrix, the stiffness matrix of the structure, centrifugal stiffening effect matrix of rotating blades, rotation softening matrix, force acting on the substructure model, displacement vector, and number of blades correspondingly. The material properties of the bladed disk are listed in Table 1.
The general forced vibration equation of the -th substructure finite element reduced order models can be expressed as:
where , is damping matrix, and is Coriolis force matrix.
Where:
where and are the first-order and second-order natural frequencies, respectively, and are the corresponding modal damping ratios.
Table 1Material properties of bladed disk
Blade material property | Property value | Disk material property | Property value |
Mass density | 4400 kg⋅m−3 | Mass density | 4700 kg⋅m−3 |
Modulus of elasticity | 113 GPa | Modulus of elasticity | 150 GPa |
Poisson’s ratio | 0.3 | Poisson’s ratio | 0.3 |
The Coriolis force matrix is generated as:
where is the shape function matrix; is the total number of elements; is the rotational matrix:
where is the stiffness matrix of the structure, is the centrifugal stiffening effect matrix of the rotating blades, and is the rotation-softening matrix.
The displacement vector is composed of the degree of freedom at the boundary and the internal freedom of the non-interface, that is:
The Eq. (2) can be expressed as:
where, is the interface force. Let the substructure of the interface to be fixed, even if , it is possible toobtain as follows:
From this, the normalized mode is solved, that is , where, – low order modal, – high order modal.
This modal set satisfies the following conditions:
where, , , is a identity matrix.
When the higher order mode sets are omitted, and the lower order mode set is selected to form the master modal set of the substructures, that is:
If the fixed interface method is used, can be expressed as follows:
Definition is the constrained modal set:
The Ritz base vector of the substructure:
Coordinate transformation is:
Through the Eq. (15), it can achieve the transformation of the equation of motion from physical coordinates to modal coordinates:
where:
The coordinate transformation of Eq. (15) ,which uses only low-order mode and ignores the high-order mode, that is used to adapt the mode truncation, so the node degree of freedom is greatly reduced, will be made for obtaining the substructure formula deduced from the Eq. (15):
If the rigid connection interface is considered, through the force balance and displacement coordination condition, it is possible to obtain as follows:
The non-independent coordinate can be transformed into the equation of motion of the generalized coordinate in the following form:
That is:
The Eq. (21) is transformed into the equation of motion of the generalized coordinate by using this form :
where:
The Eq. (22) can be adopted to solve the natural frequency of the system and the vibration mode under the generalized coordinates . The vibration mode under the generalized coordinates can be returned to the physical coordinates by the coordinate transformation from Eq. (21) and form transformation from Eq. (15), thus the vibration mode of the physical system coordinates can be obtained.
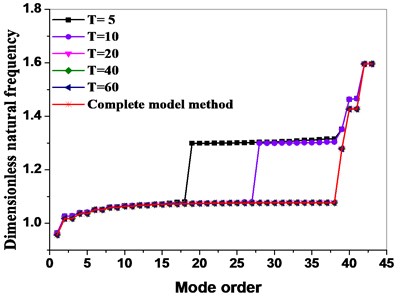
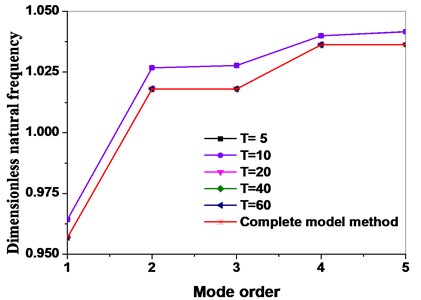
In practic, because the higher-order modals of the main interface modal are omitted, and only some low order modals are taken, thus the size of analysis and calculation are greatly reduced. By selecting different modal truncation numbers, the dynamic frequencies of the bladed disk system are obtained as shown in Fig. 2(a). When the number of mode truncation is 5 and 10, the result of natural frequency calculation in higher order mode has a larger error than that of the complete model. The influence of different modal truncation numbers on the natural frequencies within 1-5 orders are compared and analyzed, the results are shown in Fig. 2(b). The results show that the natural frequencies of low order modes are in good agreement when the mode truncation number is greater than 10.
The blades of the aeroengine compressor disk system are inevitably affected by the Coriolis force during operation. The Coriolis force effect on the vibration characteristics of the bladed disk shall be further studied on the basis of the PCMSM. Fig. 2 depicts the effect of the Coriolis force on the dynamic frequency.
Fig. 2Comparison of complete model method with dynamic reduced order models method in terms of different mode truncation numbers
a) 45-order
b) 5-order
Fig. 3Effect of coriolis force on dynamic frequency
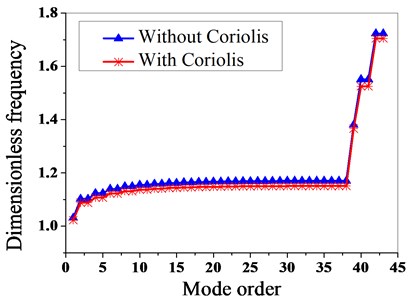
From Fig. 3, it can be seen that the dynamic frequency for a bladed disk without considering the Coriolis force effect is larger than with it, and it can be seen that the Coriolis force effect can reduce the dynamic frequency of the disk system.
3. Vibration reduction optimization of mistuned bladed disk
3.1. Vibration reduction optimization of mass mistuned bladed disk
The mass of blades is slightly different due to material and machining errors, that is, mass mistuning. The mass mistuning will lead to the unbalance effect of bladed disk system when rotated at a high speed, and then the vibration response amplitude of bladed disk system will be affected. If the blades are sorted according to the mass moment before the sorting of the mistuned blade stiffness is considered, it can effectively reduce the unbalance effect of bladed disk system.
The unbalanced moment of the th blade due to the centrifugal force is shown in Eq. (23):
where is the mass of the th blade; is the rotation angular velocity of the bladed disk system; is the th blade’ disk radius of mass centre.
The total unbalance moment of the bladed disk system is:
For the rotating bladed disk system, the total unbalance moment shall be minimized. Particle swarm optimization (PSO) is an iterative optimization algorithm, where the potential solution is first adopted as a particle, and then it initializes a group of random particles. The fitness value of the particle is determined by the optimized function.
When the minimum value of the total unbalance moment is adopted as the evaluating indicator, the fitness function is constructed as follows:
where is the total unbalance moment, is the coefficient of the penalty function, is the penalty function. According to the characteristics of the constraints, the constraints are transformed into a penalty function and added to the objective function, thus the constraint optimization problem is transformed to the unconstrained optimization problem.
The minimum unbalance moment of the bladed disk system is selected as the optimization objective function, the discrete particle swarm optimization algorithm is adopted to optimize the installation position of the blades, and a finite element model is used to calculate and verify the position of the mistuned blade position before and after the optimization. Table 2 is the blades arrangement after optimization.
Table 2Blades arrangement after optimization
Blade position | Blade number | Blade position | Blade number | Blade position | Blade number | Blade position | Blade number |
1 | 6 | 11 | 8 | 21 | 21 | 31 | 31 |
2 | 2 | 12 | 12 | 22 | 22 | 32 | 32 |
3 | 3 | 13 | 13 | 23 | 26 | 33 | 35 |
4 | 4 | 14 | 14 | 24 | 24 | 34 | 34 |
5 | 5 | 15 | 15 | 25 | 25 | 35 | 33 |
6 | 1 | 16 | 18 | 26 | 23 | 36 | 36 |
7 | 7 | 17 | 17 | 27 | 27 | 37 | 37 |
8 | 11 | 18 | 16 | 28 | 30 | 38 | 38 |
9 | 9 | 19 | 19 | 29 | 29 | – | – |
10 | 10 | 20 | 20 | 30 | 28 | – | – |
According to the data obtained from the experiment, the optimization algorithm is adopted to optimize the blade mass, and the maximum amplitude of each blade before and after optimization is calculated, as shown in Fig. 4.
It can be seen from Fig. 4 that the maximum amplitude of the mass mistuned blade decreases greatly after optimization, and the optimization effect is obvious. The maximum non-dimensional amplitude of the blade before optimization is 3.15, and the maximum amplitude occurs in blade 1. The maximum amplitude after optimization is 2.45, which occurs in blade 8. Through a comparative analysis, it can be seen that after the optimization, the maximum amplitude of the bladed disk system is reduced by 22.2 %.
The localization degree of the mistuned bladed disk system is usually evaluated by localizing the factor [1, 34, 35] as the evaluating indicator. This paper adopted the localization factor of Yuan from [1], as shown in Eq. (26), the factor takes into account the mean amplitude and variance of the maximum amplitude for each blade as the evaluating indicator:
where is the maximum amplitude vector of each blade, is the maximum amplitude average for each blade, and is the maximum amplitude variance for each blade.
Fig. 4Comparison of maximum amplitude of blades before and after optimization
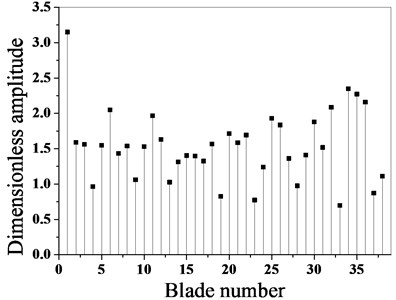
a) Before optimization
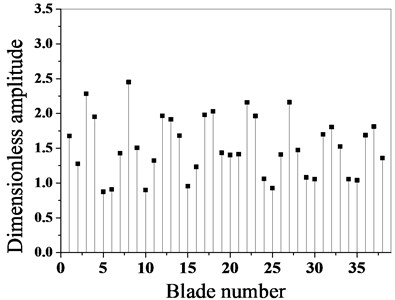
b) After optimization
In order to verify the effectiveness of the algorithm for vibration localization control of mistuned bladed disk system, in this paper, the formula of localization factor of Wang from [35] and the vibration localization factor are applied to test the algorithm, as shown in Eq. (27):
where is the number of blades, is the maximum amplitude blade number, is the maximum amplitude of blades.
According to Eq. (26) and Eq. (27), the vibration localization factors of the bladed disk system before and after optimization are calculated respectively, as shown in Table 3.
Table 3Vibration localization factor of blades before and after optimization
Localization factor calculation method | Before optimization | After optimization | Optimization range / % |
Yuan’s localization factor | 1.0292×10-8 | 7.7001×10-9 | 25.0 |
Wang’s localization factor | 3.8233×10-5 | 2.6474×10-5 | 30.8 |
From the comparative analysis of Table 2, it is found that the vibration localization factor of the optimized blade was greatly reduced by using two local factor calculation formulas as 25 % and 30.8 % respectively, and the degree of vibration localization of the bladed disk system was also reduced.
3.2. Vibration reduction optimization for simultaneous mistuning of blade mass and stiffness
In actual engineering, the blades of the bladed disk system are often under the effect of the mass mistuning and the stiffness mistuning. Most scholars have determined the form of blade stiffness mistuning for the simulation of mistuned blades, when the unbalance of a blade mass would lead to the unbalance of the whole bladed disk system. It an innovation as compared with previous engineering method to deal with blade mistuning only in the form of blade stiffness mistuning.
If an intelligent optimization algorithm is used to eliminate the unbalance of the blade system according to the mass moment of the blade, and then arrange the blade position according to the stiffness mistuning, however, the unbalance of the blade system will be disturbed, resulting in a new unbalance. In order to avoid this, the mass moment balance of mistuned blades is ensured by isolation zone. The so-called isolation zone is used to divide the whole bladed disk system into several zones, in order to ensure that the total torque of all blades in each zone and the combined torque of blades in other zones is as small as possible.
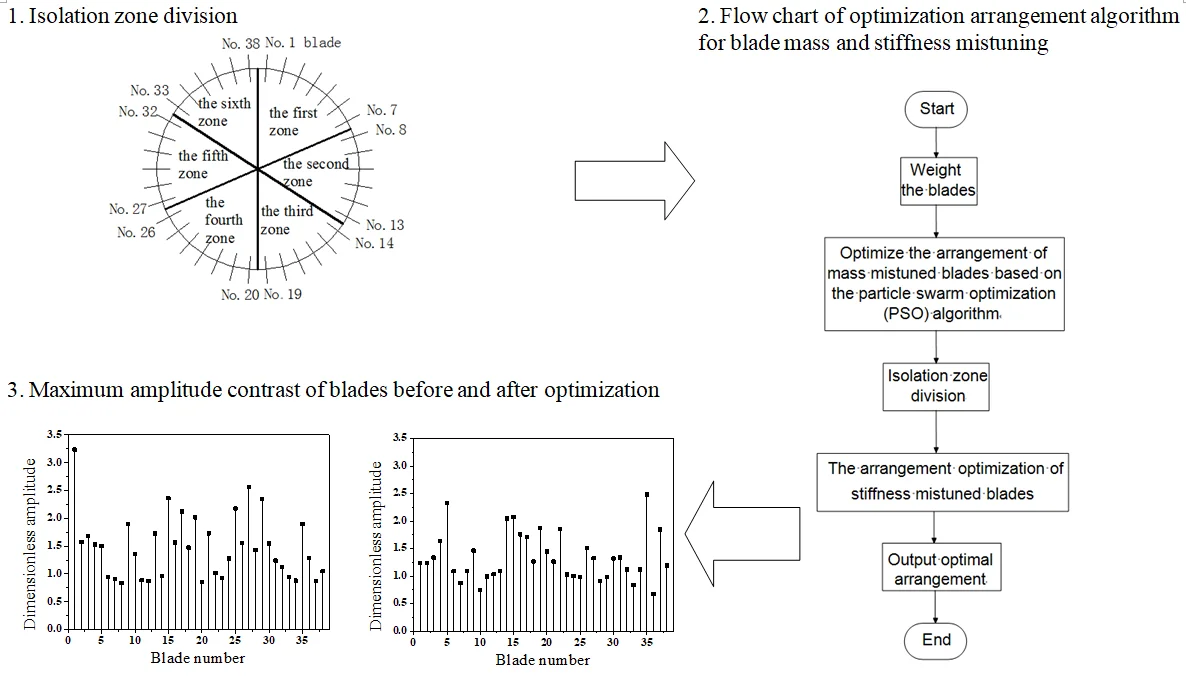
According to the model of bladed disk system adopted in this paper, the whole bladed disk system is divided into 6 zones. The 38 blades were allocated into six zones according to the form of 7, 6, 6, 7, 6, 6. Among them, the 1st-7th blades were placed into the first zone, the 8th -13th blades were into the second zone, the 14th -19th blades were into the third zone, the 20th -26th blades were into the fourth zone, the 27th-32th blades were into the fifth zone, the 33th-38th blades were into the sixth zone. The partition is shown in Fig. 5.
Fig. 5Isolation zone division
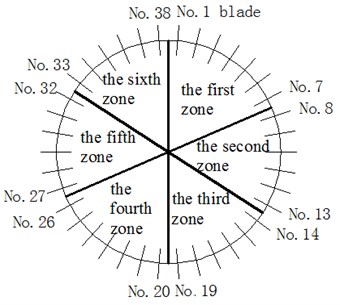
Considering the mass mistuning and stiffness mistuning of a blade, firstly, the particle swarm optimization (PSO) algorithm is used to optimize the arrangement of mass mistuned blades; the optimal arrangement scheme consists of six isolation zones. Then, the arrangement of stiffness-mistuned blades is optimized in each isolation zone based on the arrangement optimization algorithm of stiffness-mistuning according to reference [36]. The algorithm adopted the localization factor of Yuan as shown in Eq. (21) as an objective function. The algorithm is based on the finite element reduction model of mistuned bladed disk, in each iteration, only the substructure data files of blades which positions are exchanged are updated, greatly reduce the optimization time.
Finally, the optimal arrangement of mistuned bladed disk system is satisfied under the condition of minimum equilibrium torque and minimum vibration localization degree.
The flow chart of blade system optimization arrangement algorithm with both mass and stiffness mistuning is shown in Fig. 6.
3.3. Result analysis before and after optimization
The optimization algorithm is used to optimize the vibration response of mistuned bladed disk system, and the arrangement position of a mistuned blade before and after optimization is calculated and verified in a model made as per the finite element method. Table 4 is the blades arrangement after optimization of both the mass mistuning and the stiffness mistuning with the isolation zone.
Fig. 6Flow chart of optimization arrangement algorithm for blade mass and stiffness mistuning
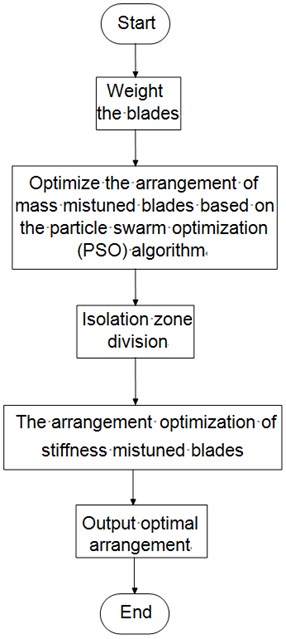
Table 4Blades arrangement after optimization of both mass mistuning and stiffness mistuning with isolation zone
Blade position | Blade number | Blade position | Blade number | Blade position | Blade number | Blade position | Blade number |
1 | 8 | 11 | 11 | 21 | 12 | 31 | 31 |
2 | 2 | 12 | 21 | 22 | 22 | 32 | 32 |
3 | 3 | 13 | 13 | 23 | 23 | 33 | 33 |
4 | 4 | 14 | 27 | 24 | 24 | 34 | 34 |
5 | 5 | 15 | 15 | 25 | 25 | 35 | 35 |
6 | 6 | 16 | 16 | 26 | 26 | 36 | 29 |
7 | 7 | 17 | 17 | 27 | 14 | 37 | 37 |
8 | 2 | 18 | 18 | 28 | 28 | 38 | 38 |
9 | 9 | 19 | 19 | 29 | 36 | – | – |
10 | 10 | 20 | 1 | 30 | 30 | – | – |
The maximum amplitude of each blade before and after optimization is calculated by using the proposed optimization algorithm, as shown in Fig. 7.
As it can be seen from Fig. 7 and Fig. 8, the maximum amplitude of the mistuned blade decreases greatly after optimization, and the optimization effect is obvious. Before optimization, the maximum dimensionless amplitude of the blade is 3.237, the maximum amplitude occurs in the blade No. 1, and the maximum amplitude after optimization is 2.483, which occurs in the blade No. 35. Through a comparative analysis, it can be seen that after optimization, the maximum amplitude of the bladed disk system is reduced by 23.9 %.
According to Eq. (26), the vibration localization factor of the bladed disk system before and after optimization is calculated, as shown in Table 5.
Fig. 7Amplitude frequency characteristics of bladed disk system before and after optimization
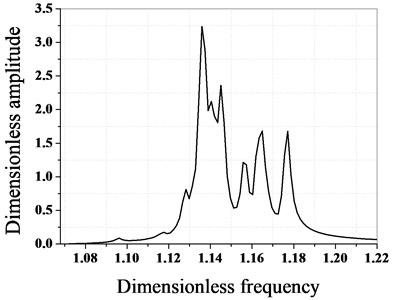
a) Before optimization
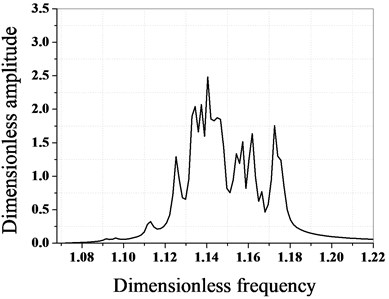
b) After optimization
Fig. 8Maximum amplitude contrast of blades before and after optimization
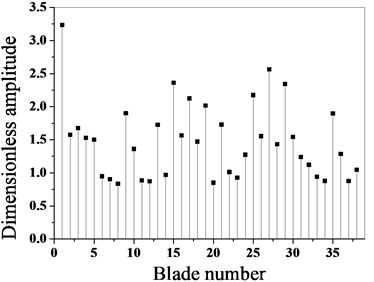
a) Before optimization
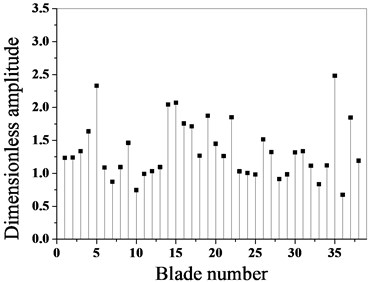
b) After optimization
Table 5Localization factor of blades vibration before and after optimization
Before optimization | After optimization | Optimization range / % |
1.2871×10-8 | 6.9146×10-9 | 46.3 |
By comparing the results of Table 5, it is found that the vibration localization factors of the optimized blade are reduced by 46.3 %, and the vibration localization degree of the bladed disk system is reduced.
4. Conclusions
In this paper, a new vibration reduction optimization method of mistuned bladed disk system, and, based on the reduced order modeling technique is proposed and the following conclusions can be made from the simulation results:
1) The unbalance moment of bladed disk is taken into account when the vibration reduction optimization is applied for the mistuned bladed disk system, which method consists in avoiding the new imbalance caused by the arrangement of blades.
2) Through a comparative analysis, it can be seen that the Coriolis force effect can reduce the dynamic frequency of the disk system.
3) The results show that the arrangement optimization method can effectively reduce the degree of vibration localization for a mistuned bladed disk system, and the effect is remarkable.
References
-
Yuan H. Q., Zhang L., Han Q. K., Song L. Optimization of mistuning blades arrangement for vibration absorption in an aero-engine based on artificial ant colony algorithm. Journal of Vibration and Shock, Vol. 31, Issue 11, 2012, p. 169-172, (in Chinese).
-
Zhao T. Y., Yuan H. Q., Yang W. J., Sun H. G. Genetic particle swarm parallel algorithm analysis of optimization arrangement on mistuned blades. Engineering Optimization, Vol. 49, Issue 4, 2017, p. 1-22.
-
Craig R. R., Bampton M. D. D. Coupling of substructures for dynamic analyses. AIAA Journal, Vol. 6, Issue 7, 1968, p. 1313-1319.
-
Bladh R., Castanier M. P., Pierre C. Component-mode-based reduced order modeling techniques for mistuned bladed disks – Part I: theoretical models. Journal of Engineering for Gas Turbines and Power, Vol. 123, Issue 1, 2000, p. 89-99.
-
Bladh R., Castanier M. P., Pierre C. Component-mode-based reduced order modeling techniques for mistuned bladed disks – Part II: application. Journal of Engineering for Gas Turbines and Power, Vol. 123, Issue 1, 2000, p. 100-108.
-
Craig R. R., Chang C. J. Free-interface methods of substructure coupling for dynamic analysis. AIAA Journal, Vol. 14, Issue 11, 1976, p. 1633-1635.
-
Craig R. R., Chang C. J. Substructure Coupling for Dynamic Analysis and Testing. NTRS, 389, p. 392-1977.
-
He H., Chen G. P., Lu Y. H. Free-interface component mode synthesis methods for damped vibration systems. Chinese Journal of Computational Mechanics, Vol. 26, Issue 6, 2009, p. 951-955, (in Chinese).
-
Ying Z. G., Qiu J. B. Hybrid modal synthesis techniques based on free interfacial and fixed interfacial substructural modes and its application. Chinese Journal of Computational Mechanics, 1997, (in Chinese).
-
Bai G. C., Li C., Zhao H. Y., Yao W. Vibratory characteristic analysis of integral mistuned bladed disk assemblies for aeroengine. Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, Vol. 229, Issue 16, 2015, p. 2921-2938.
-
Bai B., Bai G. C., Fei C. W., Zhao H. Y., Tong X. C. Application of improved hybrid interface substructural component modal synthesis method in dynamic characteristics analysis of mistuned bladed disk assemblies. Journal of Mechanical Engineering, Vol. 51, Issue 9, 2015, p. 73-81, (in Chinese).
-
Fu G. Y. A practical algorithm for assembling blades on turbine rotator. Journal of Applied Sciences, Vol. 4, 1988, p. 57-61, (in Chinese).
-
Dai Y. P., Jiang C. J., Lu S. M. Development and application of blades installation arrangement order optimizing system based on genetic algorithm. Turbine Technology, Vol. 45, Issue 5, 2003, p. 270-272, (in Chinese).
-
He E. M., Geng Y., He L., Wang P., Zhang G. D. Application of genetic algorithm in blade arrangement of engine. Mechanical Science and Technology, Vol. 22, Issue 4, 2003, p. 553-555, (in Chinese).
-
Tang S. J., Wang X., Zhu B. Research on genetic algorithm applied to sequencing of compressor vanes. Journal of Aerospace Power, Vol. 20, Issue 3, 2005, p. 518-522, (in Chinese).
-
Jia J. X., Li Q. T., Gao X. W., Chen W. Application of genetic algorithm in optimizing arrangement of engine blades based on initial unbalance. Journal of Aerospace Power, Vol. 26, Issue 1, 2011, p. 204-209, (in Chinese).
-
Choi W., Storer R. H. Heuristic algorithms for a turbine-blade-balancing problem. Computers and Operations Research, Vol. 31, Issue 8, 2004, p. 1245-1258.
-
Choi B. K. Pattern optimization of intentional blade mistuning for the reduction of the forced response using genetic algorithm. Journal of Mechanical Science and Technology, Vol. 17, Issue 7, 2003, p. 966-977.
-
Choi B. K., Lee H. S., Kim H. E. Optimization of intentional mistuning for bladed disk. Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 15, Issue 4, 2005, p. 429-436.
-
Thompson E., Becus G. Optimization of blade arrangement in a randomly mistuned cascade using simulated annealing. 29th Joint Propulsion Conference and Exhibit, 1993.
-
Bisegna P., Caruso G. Optimization of a passive vibration control scheme acting on a bladed rotor using an homogenized model. Structural and Multidisciplinary Optimization, Vol. 39, Issue 39, 2009, p. 625-636.
-
Vaiana N., Sessa S., Marmo F., Rosati L. A class of uniaxial phenomenological models for simulating hysteretic phenomena in rate-independent mechanical systems and materials. Nonlinear Dynamics, Vol. 93, 2018, p. 1647-1669.
-
Sessa S., Vaiana N., Paradiso M., Rosatia L. An inverse identification strategy for the mechanical parameters of a phenomenological hysteretic constitutive model. Mechanical Systems and Signal Processing, Vol. 139, 2020, p. 106622.
-
Vaiana N., Sessa S., Rosati L. A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena. Mechanical Systems and Signal Processing, Vol. 146, 2021, p. 106984.
-
Hohl Wallaschek A. J. A Method to reduce the energy localization in mistuned bladed disks by application–specific blade pattern arrangement. ASME Turbo Expo: Turbine Technical Conference and Exposition, 2015.
-
Yuan H. Q., Yang S. M., Wu Z. Y., Zhang L. X. Vibration reduction of mistuned blade-disc by ant colony algorithm and modal localization parameter. Journal of Northeastern University (Natural Science), Vol. 31, Issue 11, 2010, p. 1611-1614, (in Chinese).
-
Yuan H. Q., Zhang L., Han Q. K. Reducing vibration mounting optimization for aero-engine rotor mistuned blade. Journal of Vibration, Measurement and Diagnosis, Vol. 31, Issue 5, 2011, p. 647-651, (in Chinese).
-
Li L., Deng P. C., Li C., Fan Y. Research on vibration suppression of bladed disk structure with bi-periodic piezoelectric networks. Journal of Propulsion Technology, Vol. 37, Issue 1, 2016, p. 156-165.
-
Li L., Liu J. Z., Li C. Analysis on vibration suppression of mistuned bladed disk via bi-periodic distributed piezoelectric shunt damping. Journal of Aerospace Power, Vol. 32, Issue 3, 2017, p. 666-676.
-
Deng P. C., Li L., Li C. Study on vibration of mistuned bladed disk with bi-periodic piezoelectric network. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, Vol. 231, 2017, p. 350-363.
-
Deng W., Zhao H. M., Yang X. H., Xiong J. X., Sun M., Li B. Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment. Applied Soft Computing, Vol. 59, 2017, p. 288-302.
-
Deng W., Xu J. J., Zhao H. M. An Improved ant colony optimization algorithm based on hybrid strategies for scheduling problem. IEEE Access, Vol. 7, 2019, p. 20282-20292.
-
Zhang H. Y., Yuan H. Q., Yang W. J., Zhao T. Y. Study on localization influences of frequency veering on vibration of mistuned bladed disk. Journal of Mechanical Science and Technology, Vol. 31, Issue 11, 2017, p. 5173-5184.
-
Wang J. J., Yu C. B., Li Q. H. Localization characteristics of vibratory mode for bladed disk assemblies. Journal of Aerospace Power, Vol. 24, Issue 4, 2009, p. 788-792, (in Chinese).
-
Wang H. J., He Zhao E. M. Z. B. Effects of frequency veering features on mode localization of mistuned bladed disks. China Mechanical Engineering, Vol. 20, Issue 1, 2009, p. 82-85, (in Chinese).
-
Zhang H. Y., Yuan H. Q., Yang W. J., Zhao T. Y. Vibration reduction optimization of the mistuned bladed disk considering the prestress. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Vol. 233, Issue 1, 2009, p. 226-239.
About this article
This research is supported by project of the National Natural Science Foundation of China (No. 51775093), China Postdoctoral Science Foundation (2019M651147), Doctoral research initiation fund of Liaoning Provincial (2020-BS-156), Shenyang Youth Science and technology innovation talent project (RC200006) and Scientific research fund project of Liaoning Provincial Department of Education (LG202008).
