Abstract
Destructive Testing, like core drilling, remains today the only reliable method to calculate with accuracy concrete’s strength parameters. However, the damage of the constructions is always a limitation. On the contrary, Non-Destructive Tests (NDT) are fast and cost-effective which make them attractive nowadays. Nevertheless, the results of Ultrasonic Pulse Velocity (UPV) test are highly dispersed. Therefore, it is necessary to combine them along with destructive tests. The purpose of this study is to investigate the feasibility to adopt the Sonic Resonance (SR) test to determine the strength parameters of the concrete. UPV and SR were used in conjunction with the Uniaxial Compression Test. Experimental and numerical analysis were conducted. More than 200 concrete cores from existing constructions were tested and more than 70 Finite Element Method (FEM) models were simulated. The results were correlated, and two empirical equations derived. It was observed that the dispersion of the of SR alone is smaller than the UPV, but also the UPV dispersion can be narrowed as long as the Poisson’s ratio is known.
Highlights
- It is proposed UPV - SR tests to be used simultaneously, for determining the Poisson ratio and the dynamic mechanical parameters of concrete specimens
- The Concrete Core size correction factor is directly depended on the Poisson’s ratio
- The determination of the Dynamic Young’s Modulus by UPV test shows a large dispersion of results due to the range of variation of the Poisson’ ratio
- The determination of the Dynamic Young’s Modulus by SR test is derived directly from the rod’s velocity determination
- The determination of ultrasonic velocity requires the adoption of a unique Poisson's ratio value
1. Introduction
It is often necessary for engineers, to test the concrete structures in order to determine their strength and therefore constructions’ structural condition, integrity and adequacy. The most common indirect method used worldwide is the UPV which gives highly dispersed results. On the other hand, coring and testing is the most accurate and direct method but their cost might allow only a small number of tests to be carried out, which on large structures might lead to wrong results and uncertainties [1].
1.1. Ultrasonic pulse velocity (UPV)
The UPV method is an important non-destructive technique that provides reliable results based on rapid measurements using cost effective equipment. The Dynamic Elastic Modulus is associated with Ultrasonic velocity by density and Poisson’s ratio of the materials as shown in Eq. (1) and therefore, it is possible to associate it with concrete’s strength. The dynamic Young’s modulus () can be determined as follows:
where is mass density of the material, is ultrasonic pulse velocity and is Poisson’s ratio [2]. Fig. 1 shows that the velocity , relative to the compressive strength , is highly dispersed, indicating a strong dependence of the results on Poisson’s ratio [3].
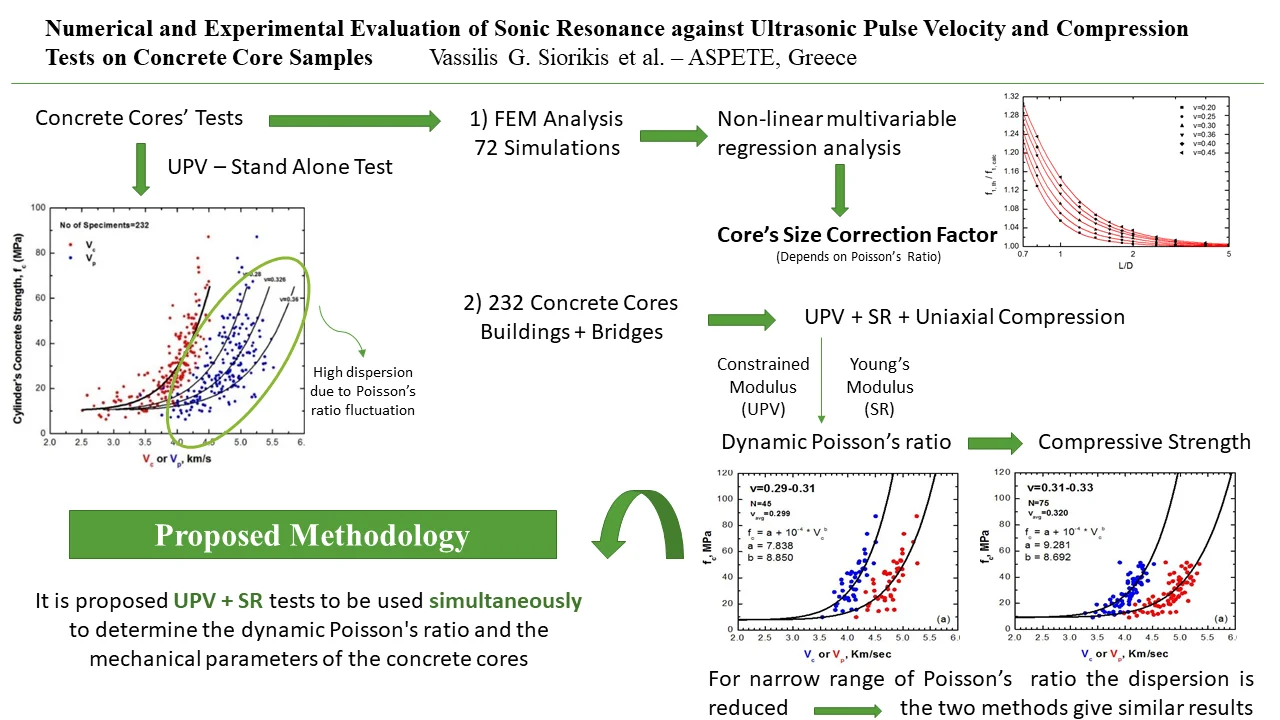
Fig. 1Correlation diagram of compressive strength fc, velocity Vp and Poisson’s ratio
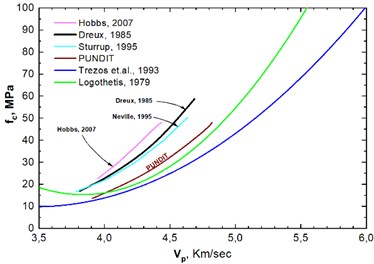
Fig. 2Correlation diagram of compressive strength fc, velocity Vp and Poisson’s ratio as resulted from the present study
1.2. Sonic resonance (SR)
The SR method is a dynamic acoustic method associated with a frequency analysis of the short-time response of a media to an impact load [4]. The principle of the method is mainly based on the calculation of the propagation velocity in finite length circular cross section rods. The propagation velocity is calculated from the resonance frequency during free oscillation of the specimen following an excitation as in Eq. (2):
where is wave propagation velocity in a cylinder with ratio > 5, is fundamental frequency of the first harmonic, is specimen’s length, is specimen’s diameter. Young’s modulus, , is directly related to the wave propagation velocity through the Eq. (3):
where is mass density of the material. Eq. (3) can be considered as the solution for a slender solid rod with a sufficient long length . In this condition the longitudinal vibration becomes a one-dimensional wave equation irrelevant to Poisson’s ratio [5].
The main drawback of SR is that in order to calculate from Eq. (2), it is necessary to have specimens with ratio > 5. In cylinders whose lengths are of the same order of magnitude as their diameters, a contraction or an extension causes non-negligible radial displacements, which depend on Poisson’s ratio [6].
When the > 5 condition is not met, a correction factor must be considered. In similar studies the dynamic Young’s modulus is calculated through the fundamental transverse frequency of a rectangular bar using Eq. (4). A correction factor is taken into account depending on the radius of gyration to the length of the specimen ratio and on Poisson’s ratio, as stated in ASTM C215 [7]:
where is Young’s modulus (Pa), is mass of the bar (kg), , are dimensions of cross section of prism (m), is length of the specimen (m), is correction factor that depends on the radius of gyration to the length of the specimen ratio and on Poisson’s ratio, is fundamental transverse frequency (Hz).
2. Numerical and experimental analysis
In this research 232 concrete cores were drilled from buildings and bridges. The construction year of the buildings was ranged between 1960 and 1990, the concrete’s compressive strength according to the European Standard EN 206 ranged between C12/15 and C20/25 and the maximum aggregate grain between 25 mm and 30 mm. In addition, four bridges were sampled. Three of them were made of conventional reinforced concrete constructed between 1960 and 1970 with compressive strength of C20/25 and natural aggregates with maximum grain of 30 mm to 35 mm. The fourth bridge was made of prestressed concrete constructed in 1970 with compressive strength of C20/25 and natural aggregates with maximum grain of 25 mm.
The cores’ length, diameter and weight were measured and tested using UPV, SR and uniaxial compression. For 95 % of the cores the diameter ranged between 9.5 cm and 10.5 cm, so that can be considered the = 1.
2.1. Numerical analysis
A finite element (FEM) numerical analysis has been carried out in order to overcome the shape influence of the cores on the results. Plaxis 2D software was used to create simulations of concrete cores using axisymmetric (Free-Free) models.
A total number of 72 simulations were created varying the following parameters: (a) Ratio = 0.7, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.5, 3.0, 4.0, 5.0, (b) Poisson’s Ratio = 0.25, 0.30, 0.36, 0.40, 0.45.
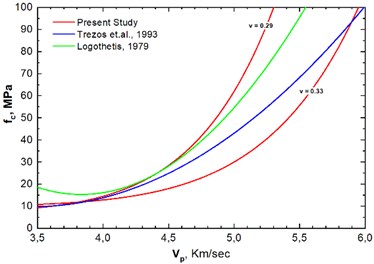
The longitudinal resonance frequencies during the free oscillation were determined from the Fast Fourier Transformation (FFT) spectra. Fig. 3 illustrates an example of a free oscillation spectrum with the values of the first and second longitudinal resonance frequencies.
The influence of the ratio of the models on the measured rod velocity can be calculated by taking a correction factor equal to the ratio of the theoretical () to the calculated (.) 1st mode through FEM analysis. In Fig. 4 the variation of the above ratio as a function of the ratio for each value of the Poisson’s ratio is shown. A non-linear multivariable regression analysis was performed according to the Levenberg and Marquardt algorithm as can be seen in Fig. 4.
Fig. 3Fourier Transform of accelerations’ timeline with first and second longitudinal resonance frequencies marked
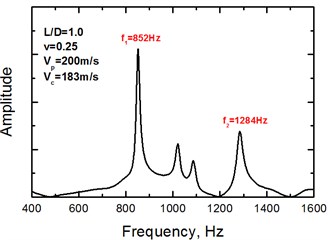
Fig. 4Theoretical to calculated 1st frequency ratio as function of L/D ratio and Poisson ratio diagram
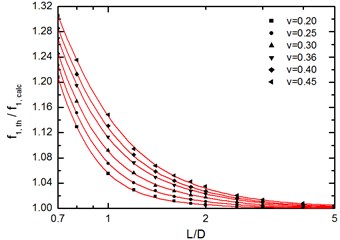
The best-fit curve that represents the variation of correction factor vs ratio has the following equation Eq. (5):
where is shape’s correction factor, ratio, , , , , coefficients that are depended on Poisson’s ratio, , derived from the same analysis and can be seen in Eqs. (6-10):
The shape’s correction factor can be calculated using Eqs. (5-10) by using the ratio and the Poisson’s ratio values.
2.2. Experimental analysis
In the experimental analysis the cores were initially tested with the NDT methods. For the UPV tests, the Proceq -Tico apparatus with a pair of 54 kHz P-wave transducers was used. The travel time of the ultrasonic pulse through the cores of known length was measured and thus the ultrasonic pulse velocity was calculated. Then the constrained dynamic modulus, through UPV was calculated using Eq. (11):
where is mass density of concrete (kN/m3), is ultrasonic pulse velocity (km/sec).
For the SR tests 54 kHz Kistler’s Accelerometer was used with a measuring range of ±50 g, sensitivity of 100.3 mV/g and weight of 10.6 grams. The signal from the accelerometers was analyzed by a Digital Signal Analyzer (DSA), resulting in the frequencies’ spectrum. From the FFT spectrum the frequency of the 1st mode, was then determined. Based on the results of the numerical analysis and applying the empirical Eq. (5) for the shape correction, the value of the was corrected. The rod velocity is calculated from the following Eq. (12):
where is specimen’s length (m) and is corrected frequency (Hz).
The Young’s modulus from Eq. (3) was then calculated using the value from Eq. (12). The Poisson’s ratio was indirectly determined from the calculated values of the two moduli (Constrained and Young’s) according to Eqs. (13-14) [8].
where , is Young’s dynamic modulus and is constrained dynamic modulus.
Finally, the uniaxial compression test was conducted and the compressive strength of concrete was calculated. In order to determine the final compressive strength, a correction was made due to the variation of the specimens’ size. The correction was based on Greek Bulletin E7 which is applicable when evaluating the strength class of existing concrete structures [9].
3. Correlation between UPV, SR and uniaxial compression strength of concrete
A correlation of the results of the three methods mentioned above was carried out. Fig. 5 illustrates the change in rod velocity vs the compressive strength seen in red while the ultrasonic velocity vs the compressive strength plotted in blue. The latter came up from three different Poisson’s dynamic ratio values determined experimentally via UPV, SR tests. It can be observed that the UPV results are significantly depended (highly dispersed) on the Poisson’s ratio.
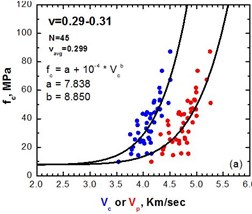
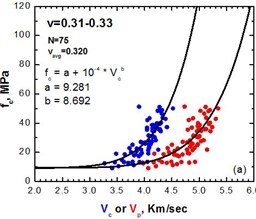
However, by solving the Eqs. (1, 3) for and narrowing the range of Poisson’s ratio we get eventually a good correlation and the dispersion is reduced to the point where the two methods give similar results as illustrated on Fig. 6.
In the compressive strength data with the propagation velocities , a curve was fitted using the least mean squares method resulting in Eqs. (14-16) as also shown on Fig. 6:
where is specimen’s compressive strength (MPa) and is rod velocity (km/sec), , are coefficients depended on Poisson’s ratio as shown in Eqs. (15, 16):
The results of the UPV tests were compared with published data [10-14]. Fig. 2 illustrates the correlation curves of compressive strength and velocity of ultrasonic propagation. The regression equations of Logothetis [10] and Trezos et al. [11-13] which also refer to concrete specimens from Greece include the results of the present study.
Fig. 5Correlation diagram of compressive strength fc, velocities Vc and Vp and Poisson’s ratio
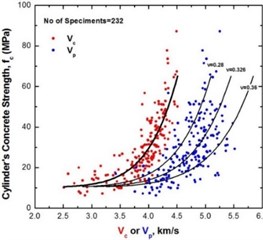
Fig. 6Diagrams of compressive strength fc vs velocity Vc for a narrow range of Poisson’s ratio, 0.29-0.31 on the left and 0.31-0.33 on the right
4. Conclusions
The UPV test is used worldwide as NDT method to evaluate the mechanical parameters of the concrete. However, the results of this method are highly dispersed. For this reason, in this research direct and indirect methods were conducted and correlated in order to determine the compressive strength of the concrete and consequently of the constructions. Two empirical equations derived, Eqs. (5, 14). More specific, a FEM numerical analysis of 72 concrete core models has been carried out in order to determine the influence of the Length to Diameter ratio on the rod’s velocity. As a result, Eq. (5) calculates the specimen’s shape correction factor. Experimental analysis was followed on 232 concrete cores from buildings and bridges. The cores were tested via UPV and SR along with Uniaxial Compression. The propagation velocities were measured through UPV and SR and the Poisson’s ratio was indirectly calculated.
As indicated in the results, the SR gives a significantly smaller scatter than the UPV. Likewise, when the two methods are combined the indirect calculate of Poisson’s ratio decreases also that dispersion. The main outcome of this research is that the Poisson’s dynamic ratio determination is crucial in order to reduce UPV dispersion and calculate the concrete’s compressive strength through SR. Therefore, it is proposed these two tests to be used simultaneously, eliminating in this way the uncertainty of the stand-alone test and thus the dispersion of results.
References
-
Guidebook on Non-Destructive Testing of Concrete Structures. International Atomic Energy Agency, Vol. 17, 2002, p. 231.
-
Panzera T. H., Christoforo A. L., Cota F. P., Borges P. H. R., Bowen C. R. Ultrasonic pulse velocity evaluation of cementitious materials, advances in composite materials – analysis of natural and man-made materials. IntechOpen, 2011, https://doi.org/10.5772/17167.
-
Christovasili K. Correlation of Ultrasonic Pulse Velocity and Sonic Resonance Test Results in determination of Compressive Strength in Concrete Cores. MSc Thesis, Hellenic Open University, Greece, 2018, (in Greek).
-
Lu X., Sun Q., Feng W., Tian J. Evaluation of dynamic modulus of elasticity of concrete using impact-echo method. Construction and Building Materials, Vol. 47, 2013, p. 231-239.
-
Wang J. J., Chang T. P., Chen B. T., Wang H. Determination of Poissons ratio of solid circular rods by impact-echo method. Journal of Sound and Vibration, Vol. 331, Issue 5, 2012, p. 1059-1067.
-
Nieves F. J., Gascón F., Bayón A. Measurement of the dynamic elastic constants of short isotropic cylinders. Journal of Sound and Vibration, Vol. 265, Issue 5, 2003, p. 917-933.
-
Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens 1. ASTM Standard C215, 2015.
-
Mavko G., Mukerji T., Dvorkin J. P-wave modulus – Wikipedia, 2003, https://en.wikipedia.org/wiki/P-wave_modulus.
-
Assessment of Concrete’s Strength Classification of Existing Structures. Greek Ministry of Environment Physical Planning and Public Works, 1997, http://fakisc.weebly.com/uploads/3/2/7/6/3276490/Εγκύκλιος_7_28-3-1997.pdf, (in Greek).
-
Logothetis L. A Contribution to the In-Situ Assessment of Concrete Strength by Means of Combined Non-Destructive Methods. Ph.D. Thesis, National Technical University, Athens, 1978, (in Greek).
-
Trezos C., Papakyriakopoulos P., Spanos C. Calibration of the Rebound Hammer and Pulse Velocity Methods Through in Situ Concrete Cores and Standard Cube Specimens. Technical Chamber of Greece, 1993, p. 1-8, http://portal.tee.gr/portal/page/portal/teeait/drast/hmerida-11-12-2004/TAB5851916/CalibrationUpvRebound.pdf, (in Greek).
-
Trezos K. Assessment of in Situ Concrete’s Durability. Technical Chamber of Greece, 1999, p. 1-33, http://portal.tee.gr/portal/page/portal/teeait/drast/hmerida-11-12-2004/TAB5851916/InsituCoresUpvRebound.pdf, (in Greek).
-
Spanos C., Spithakis M., Trezos C. In Situ Assessment of Materials’ Charactheristics. Technical Chamber of Greece, 2001, p. 53–62, http://portal.tee.gr/portal/page/portal/teeait/drast/hmerida-11-12-2004/TAB5851916/TEEInsituAssessmentTextBook.pdf, (in Greek).
-
Hobbs B., Tchoketch Kebir M. Non-destructive testing techniques for the forensic engineering investigation of reinforced concrete buildings. Forensic Science International, Vol. 167, Issues 2-3, 2007, p. 167-172.
About this article
This work has been financed by the Greek School of Pedagogical and Technological Education through the operational program “Research strengthening in ASPETE”– Project 80154: “Determination of Compressive Strength and Other Mechanical Concrete Parameters by Sonic Resonance (Experimental and Numerical Investigation)”.
