Abstract
This paper described a continuous load one-dimensional consolidation apparatus developed and improved, conducted an axial cyclic loading and unloading test of saturated soft clay. It can be known from the experimental comparison that during the unloading period, a stress strain curve of saturated soft clay is made hyperbolic. During the reloading period, when the loading quantity is less than the unloading quantity, the curve is hyperbolic, and when the loading quantity is greater than unloading quantity the curve is a straight line which keeps hardening. The plastic deformation and elastic deformation of test samples produced in the test have linear relation with the unloading level. On the basis of the original constitutive relation, axial circulation loading and unloading constitutive equation have been established using the loading axial stresses, initial tangent modulus, maximum unloading axial strain and its initial secant modulus as parameters. The reliability of equations was verified as well. The analysis of various plastic hysteresis reveals that as the unloading stress level increases, the hysteresis increases too and conforms to the quadratic curve relationship. This provides a certain engineering practice value for the strength and deformation characteristics of soft soil under cyclic loading.
Highlights
- Described a continuous load one-dimensional K0 consolidation apparatus developed and improved.
- On the basis of the original constitutive relation, axial circulation loading and unloading constitutive equation have been established.
- This provides a certain engineering practice value for the strength and deformation characteristics of soft soil under cyclic loading.
1. Introduction
With the rapid development of the economy, the construction of transportation infrastructure along the coast and along the Yangtze River has also developed rapidly. More and more ports, airports, highways and railway projects, bridge and tunnel projects, subways and river tunnel projects, underground shopping malls, hydropower stations, and large oil tanks have been built. These projects are often subject to variable loads. Therefore, the unloading effect can be seen, such as tunnel excavation and support, geological tectonic movement, pier foundation rock, etc., which are actually the process of repeated loading and unloading of rock and soil.
Soft clay has obvious rheology. For buildings built on soft soil, the deformation and strength characteristics of soft clay are closely related to its stress state and loading history. Compared with the common uniaxial and triaxial tests, the loading and unloading test can reveal more mechanical phenomena. At present, there are many studies on the deformation characteristics of rock and soil under cyclic loading, while the one-dimensional consolidation axial cyclic loading and unloading tests under state are still less [1, 2]. Therefore, correct understanding of the strength and deformation characteristics of soft soil under cyclic loading has a certain engineering practice value [3, 4].
In this paper, through the self-developed continuous loading consolidation instrument, a cyclic loading and unloading test of a certain depth of saturated soil was carried out, and the deformation characteristics of saturated soft clay under cyclic loading, unloading and reloading conditions were analyzed. The relationship between soil elasticity, plastic deformation and stress level during the loading and unloading process is established, and the corresponding expression is established to facilitate the practical application of the project. Finally, based on the experimental results, the cyclic loading and unloading constitutive equation was established [2, 5, 6]; and the plastic hysteresis energy was calculated and fitted. It provides a theoretical basis for deformation prediction of saturated clay foundation, and provides guidance for practical application of engineering.
2. Cyclic loading and unloading test
The test uses soft soil, which is gray, soft and plastic, and has a large amount of organic matter. According to indoor geotechnical tests, the sample height is 40 mm, and the cylinder diameter is 61.8 mm, the plastic limit of the sample is 31, and the liquid limit is 59, plastic index 28. This sample was saturated with vacuum saturated gas. After saturation, the saturation level of soil sample was 99 %, 1.69 g/cm3, and 1.44. After the sample is saturated, the cyclic loading and unloading test is performed. The test is made as per the “load-unload-reload” principle. The test has 5 levels of incremental loading and unloading, as shown in Table 1.
Table 1Loading and unloading test program
Loading and unloading level | Loading (kPa) | Unloading (kPa) |
1 | 0-100 | 100-0 |
2 | 0-200 | 200-0 |
3 | 0-300 | 300-0 |
4 | 0-400 | 400-0 |
5 | 0-500 | Test stopped |
3. Test results and analysis
3.1. Unloading curve analysis of – consolidated saturated clay
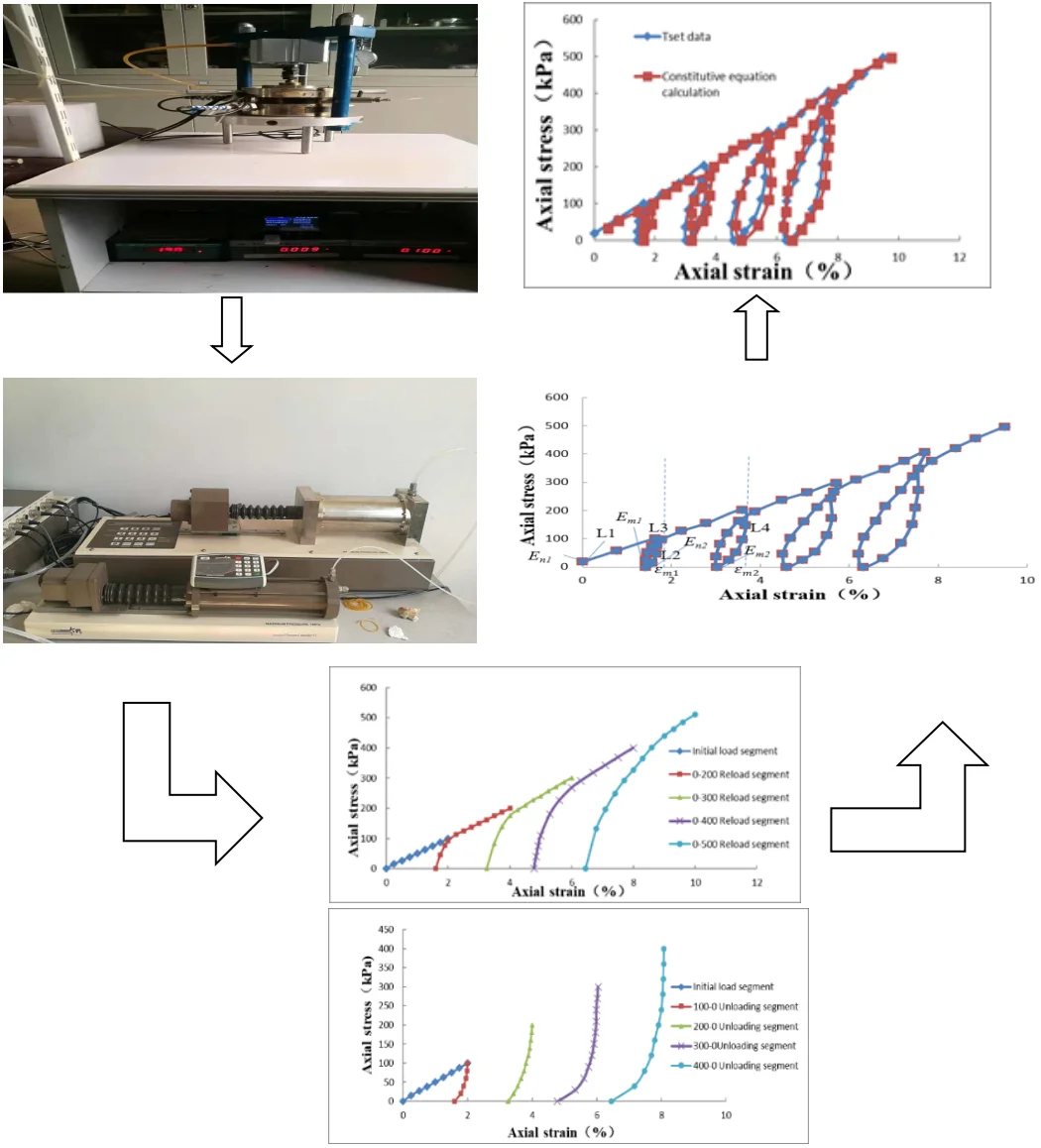
The axial stress and strain of – consolidated saturated clay in the unloading conditions at all levels is shown in Fig. 1. The test results show that the change trend of the unloading curves at all levels is the same. The trend of the initial unloading curve is steep, which can be approximated as a straight line. while unloading time is increasing, the unloading is in the form of a curve. The unloading curve is mainly composed of curved segments, which also explains the non-linear characteristics of saturated soft soil, which is different from the rock unloading curve. The deformation modulus of saturated soft soil and the plastic soil deformation of the soil can be obtained by the unloading curve. The surrounding rock of the tunnel is in the unloading environment for a long time. By obtaining the unloading curve in the – consolidated, the deformation modulus of unloading curve used in modeling calculation is closer to the actual project.
Fig. 1Axial stress and strain diagram in unloading phase
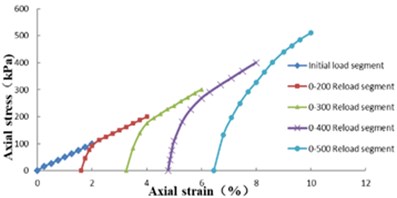
Fig. 2Axial stress and strain diagram in Reloading phase
3.2. Reloading curve analysis of – consolidated saturated clay
The axial stress and strain of – consolidated saturated clay in the Reloading conditions at all levels is shown in Fig. 2. Compared with Fig. 1, the reloading curve and the unloading curve are not caused by the soil plasticity. From the point of view of the reloading curve, the reloading curve approximates a curve before rising to the load of the upper unloading curve. When the load exceeds the load of the upper unloading curve, the reloading curve approximates a straight line and rises along the initial load curve. The loading-unloading curves of unsaturated soils and general foundation soils are basically the same or similar to the initial tangent slope of the initial loading curve, but the slope of the loading-unloading curves of saturated soft soils studied in this experiment is quite different, mainly because the loading-unloading process has a great influence on the physical and mechanical properties of saturated soft soils. The result also shows that the elastic deformation of saturated soft soils is relatively small. In general, the tangent slope of the reloading curve is used to represent the deformation modulus of the reloading curves at all levels, and the deformation characteristics of the reloading curve are described by the average value of the deformation modulus of the reloading curves at all levels [3].
During the operation of oil tank, the foundation soil was in the state of cyclic loading and unloading, and when the pressure applied in the tank was less than the initial stress of the foundation soil, the modulus of deformation of the reloading curve under – consolidated was closer to the actual situation when calculating and selecting parameters.
3.3. Constitutive relation of loading and unloading
3.3.1. Loading-unloading constitutive equation
In the stress-strain relationship curve of axial cyclic loading and unloading, the tangent slope corresponding to the axial force of 0 on the curve is usually taken as the initial deformation modulus of the specimen during loading or unloading. The hyperbolic equation is determined by the modulus, and the initial deformation modulus of the next unloading curve and the reloading curve is determined by the former loading curve and unloading curve [5-8], thus establishing the cycle.
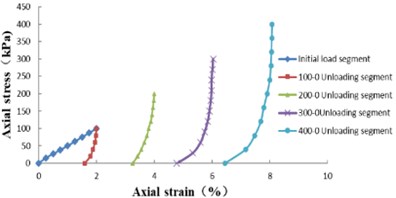
In this work, two-stage cyclic loading and unloading are described, as shown in Fig. 3. It can be seen that is the initial loading curve, is the unloading curve, is the reloading curve, is the second stage unloading curve, and the initial deformation modulus corresponding to the four curves is , , , ; unloading vertices are (,) and (,), and and are the strains corresponding to zero axial stress during unloading, i.e., the plastic deformation of the sample; is the maximum axial stress when the axial strain tends to infinity in the loading stage, and and are the maximum axial strains when the axial stress of the unloading curve tends to infinity. The loading curve equation can be expressed by hyperbolic equation as follows:
The equation of the unloading curve can be written as follows:
The modulus of deformation during unloading can be expressed as:
According to the same method, the expressions of stress and modulus of deformation can be obtained as follows:
According to the above method, the stress-strain equation and deformation modulus of saturated soft soil under cyclic loading and unloading can be expressed as follows.
Initial loading curve:
Unloading curve:
Reloading curve:
In which, 1, 2,…, Eqs. (6-10) contain the constitutive equations of cyclic loading-unloading curve and the expression of deformation modulus of saturated soft soil. The parameters in the formula can be obtained from cyclic loading-unloading test in conventional consolidation apparatus. The axial strain at a certain time can be calculated by applying the applied axial stress.
Fig. 3Axial stress and axial strain diagram
3.3.2. Verification of constitutive equation
The above Eqs. (6), (7), (9) are constitutive equations for cyclic loading and unloading tests of saturated soft soils. The equation parameters are obtained by conventional cyclic loading and unloading tests. These parameters are arranged as shown in Table 2.
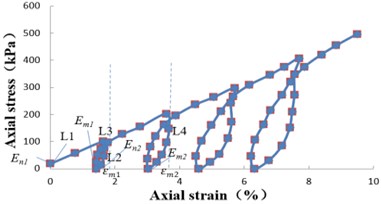
By substituting the parameters in Table 2 into Eqs. (6), (7), (9), the axial strain corresponding to arbitrary axial stress under cyclic loading and unloading can be obtained. The constitutive equation calculation and experimental data are compared and analyzed, as shown in Fig. 4.
Fig. 4Constitutive equation calculation and test data contrast – analysis diagram
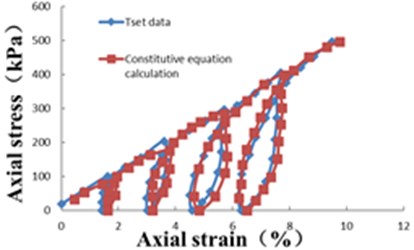
From Fig. 4, it can be seen that there are some differences between the calculated results and the test results, but the overall trend is the same, that shows that the constitutive equation can be used to describe the cyclic loading and unloading characteristics of saturated soft soil.
Table 2Constitutive equation parameters
Loading (KPa) | Loading curve | Unloading curve | |||
(KPa) | (%) | (%) | |||
100 | 88.5 | 193 | 67.8 | 2.14 | 1.597 |
200 | 370.4 | 227 | 57.3 | 4.33 | 3.195 |
300 | 476.2 | 345 | 36.5 | 6.33 | 4.723 |
400 | 555.5 | 477 | 35.7 | 8.52 | 6.385 |
500 | 588.2 | 625 | – | – | – |
4. Conclusions
Based on the analysis of the test data of saturated soft soil under axial cyclic loading and unloading, the following conclusions are drawn:
1) The change trend of the unloading and reloading curves at all levels is the same. The specimen deformation shows a non-linear characteristic. The unloading and reloading curves mainly consist of curve segments. When the load of a reloading curve exceeds the unloading load of the higher level, the curve approximates to a straight line and rises along the initial loading curve. These laws can be verified by the analysis of deformation modulus in the test process.
2) The hyperbolic constitutive equations of axial stress and strain in unloading and reloading processes are derived by using the initial deformation modulus of loading and unloading curves, and their reliability is verified. This provides a certain engineering practice value for the strength and deformation characteristics of soft soil under cyclic loading.
3) According to the cyclic test, the law that the strain of the saturated soil increases with the number of cyclic loading and unloading under the cyclic load is obtained, and the ratchet effect due to strain lag and other reasons is obtained. The first cycle of loading and unloading has a significant effect on the sample. For saturated soft soils, plastic deformation is mainly caused by the first cyclic loading and unloading, and the elastic deformation of the subsequent cyclic loading and unloading still accounts for a large proportion.
References
-
Huo Hai-Feng Mechanical Properties of Saturated Clay Under Circulating Load. Tianjin University, Tianjin, 2012.
-
Li Zhi-Xing Saturated Soft Clay Foundation Under Cyclic Loading One Dimensional Nonlinear Consolidation Theory and Pore Water Pressure Calculation. Wuhan University of Technology, Wuhan, 2006.
-
Zhou Jian, Gong Xiao-Nan, Li Jian-Qiang Experimental study of saturated soft clay under cyclic loading. Industrial Construction, Vol. 30, Issue 11, 2000, p. 43-47.
-
Liang Xu, Cai Yuan-Qiang, Wu Shi-Ming, Pan Xiao-Dong One dimensional consolidation analysis of saturated soil in the Half-permeable boundary under circulating load. Journal of Hydraulic Engineering, Vol. 31, Issue 7, 2002, p. 31-35.
-
Luo Ting Constitutive Relation of Soils. China Communications Press, Beijing, 2010.
-
Zhu Zhao-Xiang Material Constitutive Relation Theory Handout. Science Press, Beijing, 2015.
-
Yang Chun-He, Ma Hong-Ling, Liu Jian-Feng Study of deformation of rock salt under cycling loading and unloading. Rock and Soil Mechanics, Vol. 30, Issue 12, 2009, p. 3562-3567.
-
He Shi-Xiu, Long Li-Hua, Yang Xue-Qiang Study on the unloading yield characteristic test of clay soil. Rock and Soil Mechanics, Vol. 29, 2008, p. 449-452.
-
Qian Jiahuan, Yin Zongze Geotechnical Principle and Calculation. Hydraulic Power Press, Beijing, 1999.
