Abstract
In order to study the reasonable cable force of a highway and rail dual-purpose steel truss cable-stayed bridge in the completion state, this paper employs four methods, i.e. the rigid supported continuous beam method, bending minimum energy method, influence matrix method and BP neural network method combined with a genetic algorithm. The Baijusi Yangtze river bridge, with a main span of 660 m in the completion state, is chosen as the object of study. Through comparative analysis, it is found that the rigid supported continuous beam combined with the influence matrix method can determine the reasonable cable force of the highway and rail dual-purpose steel truss cable-stayed bridge more quickly and effectively.
Highlights
- The reasonable cable force of a highway and rail dual-purpose steel truss cable-stayed bridge in the completion state is investigated using four methods
- The cable force of the bridge in the completion state is optimized by the rigid supported continuous beam combined with the influence matrix method
- The rigid supported continuous beam combined with the influence matrix method can determine the reasonable cable force
1. Introduction
With the development of steel strength and steel truss cable-stayed bridge construction technology, the steel truss cable-stayed bridge has aroused increasing attention in the field of long-span highway and rail dual-purpose cable-stayed bridges [1]. The distribution of the bridge’s internal forces in the completion state is the most obvious indicator of the design quality of a cable-stayed bridge [2]. Accordingly, it is critical to determine a set of cable forces which ensure a cable-stayed bridge satisfies reasonable completion state requirements [3].
There are numerous methods of optimizing the cable force of cable-stayed bridges in a reasonable completion state at home and abroad. The primary methods are the rigid support continuous beam method, zero displacement method, specified stress method, internal force balance method [4], bending energy minimum method [5], bending moment square and minimum method, influence matrix method [6]and BP neural network method [7]. Steel truss cable-stayed bridges are often very complex in structure and have thousands of discrete members. Thus, traditional research methods are no longer applicable for optimizing the cable force in a reasonable completion state. The existing methods of improving the cable force of steel truss cable-stayed bridges are rare and difficult to promote [8].
By summarizing the previous studies and taking the Baijusi Yangtze river bridge in Chongqing as the object of study, the reasonable cable force of a highway and rail dual-purpose steel cable-stayed bridge in the completion state is analyzed, and a method for quickly determining the reasonable cable force is determined.
The novelties of this paper are as follows: firstly, compared with the traditional methods, the rigid supported continuous beam method combined with the influence matrix method can take into consideration the influence of the horizontal component of the stay cable forces when determining the reasonable cable force. Secondly, in most cases, the cable force in the reasonable completion state is optimized by a single method. There are few cases where two or more methods are combined for cable force optimization analysis.
2. Project overview
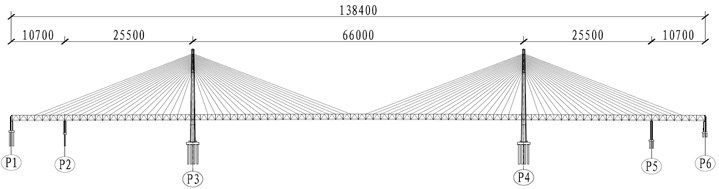
The bridge is a steel truss double-tower, double-cable plane highway and rail dual-purpose cable-stayed bridge. The ratio of the side to the middle span reaches 0.341. The span combination of the bridge is 107+255+660+255+107 = 1384 m and the ratio of the side to the middle span reaches 0.341. The geometry and main dimensions of the bridge are shown in Fig. 1.
Fig. 1Standard deck shape and dimensions (unit: cm)
3. Finite element model
In this study, the special Midas Civil 2015 finite element software for bridge structures is employed to build the computational model. The main beam trusses, beams, longitudinal beams and pylons are simulated by the spatial beam element. Taking shear deformation into account, the orthotropic bridge decks are simulated by the ribbed plate element, and the stay cables are simulated by tension-only trusses. The bridge is a cable-stayed bridge with a supporting system and a total of 15588 nodes and 35088 units. The full-bridge finite element model is shown in Fig. 2.
Fig. 2The finite element model of the Baijusi Yangtze river bridge

4. Rigid supported continuous beam method cable force improvement calculation
4.1. Bridge cable force output
The bridge has 160 cable-stayed cables in total. For the convenience of the following discussion, according to the structure’s principle of symmetry, it is assumed that the forces of the two cables in the transverse direction of the bridge are equal. The number of stay cables decreases from T20 to T1 from the shore side to the bridge tower and increases from M1 to M20 from the bridge tower to the middle of the span, as shown in Fig. 3.
The vertical reaction forces are calculated and analyzed, and the initial bridge cable forces are then determined. The results are shown in Table 1.
Fig. 3Labels of the cables
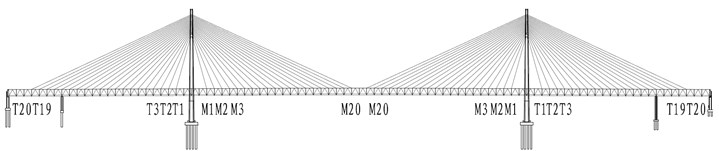
Table 1The initial bridge cable force table
Cable labels | Cable force (kN) | Cable labels | Cable force (kN) | Difference value | Percentage |
T1 | 6426 | M1 | 6428 | –2 | 0 |
T2 | 4582 | M2 | 4589 | –7 | 0 |
T3 | 4281 | M3 | 4344 | –62 | –1 |
T4 | 4295 | M4 | 4297 | –2 | 0 |
T5 | 4449 | M5 | 4451 | –1 | 0 |
T6 | 4683 | M6 | 4688 | –5 | 0 |
T7 | 4931 | M7 | 4944 | –12 | 0 |
T8 | 5164 | M8 | 5198 | –34 | –1 |
T9 | 5349 | M9 | 5430 | –82 | –2 |
T10 | 5613 | M10 | 5605 | 8 | 0 |
T11 | 5952 | M11 | 5851 | 101 | 2 |
T12 | 6387 | M12 | 6185 | 203 | 3 |
T13 | 6974 | M13 | 6439 | 535 | 8 |
T14 | 8275 | M14 | 6679 | 1596 | 19 |
T15 | 8265 | M15 | 6920 | 1345 | 16 |
T16 | 5160 | M16 | 7168 | –2008 | –39 |
T17 | 9000 | M17 | 7452 | 1548 | 17 |
T18 | 10024 | M18 | 7909 | 2116 | 21 |
T19 | 10002 | M19 | 8574 | 1428 | 14 |
T20 | 14151 | M20 | 11575 | 2575 | 18 |
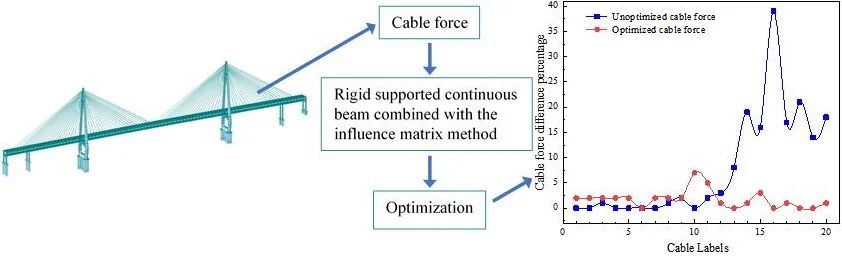
It can be concluded from the data in Table 1 that the cable-stayed cable force varies significantly around the auxiliary pier. The difference between the cable force of the symmetrical cable-stayed cables to the left and right of the bridge tower at the position of the auxiliary pier (T16) reaches 39 %. The cable force value shows a large jump, which is not consistent with the symmetry principle and the cable force distribution requirements in the reasonable completion state. It should be adjusted twice.
4.2. Cable force adjustment combined with the influence matrix method
The cable force adjustment should follow the distribution principle of the reasonable bridge cable force [9]. In the meantime, the difference between the force of the symmetrical cable-stayed cables to the left and right of the bridge tower should not be large due to the symmetrical arrangement of the cables. The adjusted cable force is shown in Table 2.
Table 2 suggests that the cable force is uniform and does not experience a jump. The cable forces on both sides of the bridge tower are basically symmetrical and satisfy the requirements of the reasonable completion state.
5. Comparative analysis
5.1. Comparison with the minimum bending energy method
The rigid supported continuous beam method mainly considers the alignment and internal force of the main girder and usually neglects the force of the bridge tower. The bending minimum energy method considers the forces of the main beam and the bridge tower, but its major beam alignment control is inferior to that of the rigid supported continuous beam method. The starting points of the two methods are inconsistent, resulting in a great difference in the initial values of the cable forces adjusted by the influence matrix combined with the rigid support continuous beam method and the bending minimum energy method.
The results show that, based on the two methods and combined with the adjustment of the influence matrix, the control conditions, such as the alignment and stress of the main girder and the deformation and stress of the bridge tower, all meet the requirements of the design specifications, and there are sufficient reserves for the live load. The former is relatively superior to the latter in controlling the alignment of the main beam, whereas the latter is better than the former in controlling the main beam stress.
Table 2Cable force adjusted by the rigid continuous beam supporting method
Cable labels | Cable force (kN) | Cable labels | Cable force (kN) | Difference value | Percentage |
T1 | 5537 | M1 | 5627 | –90 | –2 |
T2 | 4780 | M2 | 4871 | –91 | –2 |
T3 | 4848 | M3 | 4744 | 105 | 2 |
T4 | 4739 | M4 | 4635 | 104 | 2 |
T5 | 4937 | M5 | 4831 | 107 | 2 |
T6 | 4947 | M6 | 4936 | 11 | 0 |
T7 | 5253 | M7 | 5339 | –86 | –2 |
T8 | 5465 | M8 | 5352 | 113 | 2 |
T9 | 5877 | M9 | 5760 | 116 | 2 |
T10 | 5600 | M10 | 5973 | –374 | –7 |
T11 | 6110 | M11 | 6386 | –275 | –5 |
T12 | 6618 | M12 | 6700 | –81 | –1 |
T13 | 6826 | M13 | 6811 | 15 | 0 |
T14 | 7322 | M14 | 7411 | –89 | –1 |
T15 | 7224 | M15 | 7414 | –191 | –3 |
T16 | 7717 | M16 | 7713 | 3 | 0 |
T17 | 7920 | M17 | 7817 | 103 | 1 |
T18 | 8226 | M18 | 8222 | 4 | 0 |
T19 | 8234 | M19 | 8230 | 5 | 0 |
T20 | 8337 | M20 | 8233 | 105 | 1 |
5.2. Comparison with the influence matrix method
In this study, Midas Civil is employed to build the finite element model while ignoring the nonlinear influence of the cable in the completion state. The truss element is adopted to simulate the cable-stayed cable, and the “unknown load factor method” in Midas Civil is employed to solve and yield the influence matrix. It incorporates the “adjust cable function” to adjust the full-bridge alignment and internal force.
The results suggest that the cable forces obtained using the two methods follow the reasonable bridge cable force distribution law, and there is a huge difference at T1 (M1). However, when the rigid support continuous beam method is combined with the influence matrix method, the difference is smaller at T1 and M1, which can better satisfy the stress requirements of the main beam during construction. In general, the two methods differ slightly in controlling the alignment and stress of the main beam, but the distribution law is the same. Both methods satisfy the requirements of the reasonable completion state.
5.3. Comparison with BP neural network combined with genetic algorithm
In the present paper, based on the cable force optimization principle of the genetic algorithm and BP neural network (i.e., using the powerful nonlinear mapping function of the BP neural network to build a network model of the mapping relationship between the bridge cable force and the control parameters), the crossover, mutation and selection algorithms of the genetic algorithm are used for global optimization.
The results suggest that the cable forces obtained by the two methods satisfy the distribution law of reasonable cable force. The difference between the two is small, and the maximum percentage is less than 2 %. The two methods adequately control the stress and alignment of the main beam and satisfy the specification requirements. The overall distribution of the cable force of the rigid supported continuous beam combined influence matrix method is smaller than that of the BP neural network combined with the genetic algorithm method, and the stress distribution is slightly uniform.
6. Conclusions
The finite element model of the Baijusi Yangtze River Bridge is established using Midas Civil 2015. Four methods are employed to determine the reasonable cable force of the bridge in the completion state, including the rigid support continuous beam method, bending energy minimum method, influence matrix method and BP neural network method combined with genetic algorithm. By comparing and analyzing the calculation results of each method and the complexity of the solution process, the following conclusions are drawn:
1) The force of the rigid support continuous beam method is clear and the alignment control of the main beam is good. However, this method does not consider the impact of the horizontal component of the cable-stayed cable. The displacement at the top of the bridge tower and the stress at the bottom of the bridge tower is too large. The cable force should be adjusted.
2) The minimum bending energy method considers the stress of the main beam and the bridge tower. The bending moment distribution of the main beam is uniform, but the main beam alignment control is poor, and it is difficult to modify the section bending stiffness for a highway and rail dual-purpose steel cable-stayed bridge with discrete members and variable cross-sections.
3) The influence matrix method is capable of controlling the multi-objective parameters by the single variable of the bridge cable force, and it is convenient for the realization of the objective function. The internal force, stress and deformation conditions of the bridge tower in the completion state are relatively moderate. This method can also simultaneously satisfy the requirements of the force and alignment of the tower beam. However, the control parameters should be calculated or have empirical values, and the solution process is complicated and cumbersome.
4) The BP neural network combined with genetic algorithm can quickly solve multiple sets of reasonable cable forces in the completion state, but it depends too heavily on the sample and the sampling process is complicated and time-consuming. The objective function directly determines the prediction accuracy and should be adjusted repeatedly.
5) By fully considering the stress of the main beam, and correcting the influence of the horizontal component force on the bridge tower and the unevenness of the cable force, the rigid support continuous beam combined with the influence matrix method is able to quickly determine the reasonable cable force of the steel truss cable-stayed bridge in the completion state. In comparison with the trial of the control parameters by the single influence matrix, the modification of the bending stiffness of the section by the bending minimum energy method, and the generation of the BP neural network and genetic algorithm samples, this method is simple and applicable, and can satisfy the actual needs of the project.
References
-
Haifan X., Dingjun W. The present situation and prospect of railway bridge in China. Railway Construction Technology, Vol. 2, 2001, (in Chinese).
-
Wang P. H., Tseng T. C., Yang C. G. Initial shape of cable-stayed bridges. Computers and Structures, Vol. 47, Issue 1, 1993, p. 111-123.
-
Kim K., Lee H. S. Analysis of target configurations under dead loads for cable-supported bridges. Computers and Structures, Vol. 79, Issues 29-30, 2001, p. 2681-2692.
-
Dong-Huang Y., Xue-Wen L., Guang-Dong L., et al. Deciding the reasonable finished dead state of the main beam of cable-stayed bridges using stress balanced method. China Journal of Highway and Transport, Vol. 13, Issue 3, 2000, (in Chinese).
-
Xiyao Y., Shuping Y., Min C. Determining of rational completion cable forces of cable-stayed bridges by minimum bending energy method. Anhui Architecture, Vol. 2, 2014, (in Chinese).
-
Peng L., Ru-Cheng X., Xue-Song Z. Practical method of optimization of cable tensions for cable-stayed bridges. Journal of Tongji University, Vol. 31, Issue 11, 2003, (in Chinese).
-
De-Wei C., Zhi-Zhou B., Zheng H. Determination of initial cable forces for prestressed concrete cable-stayed bridges with genetic algorithm. Journal of Tongji University, Vol. 31, Issue 1, 2003, (in Chinese).
-
Xiaohui X. Cable Force Optimization under Finished State and Determining of Reasonable Construction State of Multi-Pylon Cable-Stayed Bridge. Southwest Jiaotong University, 2010, (in Chinese).
-
Jia-Wu M. Study for Design Theories of Superlong Span Cable-Stayed Bridges. Tongji University, 2006, (in Chinese).
About this article
This study was funded by the Science and Technology Research Program of Chongqing Municipal Education Commission under the Grant number KJZD-K201802501 and the Graduate Scientific Research Innovation Foundation of Chongqing under the Grant number CYB17042 and CYB18022.
