Abstract
In the service period, a crack may appear in some engineering structures. The development of accurate and effective methods for crack damage detection has become a topic of great importance. In this paper, a nonlinear damage detection method based on the improved Dempster-Shafer (D-S) theory and time domain model is presented. First, acceleration responses in the undamaged and damaged states are measured by using accelerometers. Then, acceleration responses are utilized to establish an autoregressive (AR) model, and residual time series of acceleration responses are used to establish an autoregressive conditional heteroskedasticity (ARCH) model. A cepstral metric conversion (CMC) method based on the AR model is employed to obtain local damage solution and an autoregressive conditional heteroskedasticity conversion (ARCHC) method based on ARCH model is presented to acquire another local damage solution. Finally, the D-S theory is applied to detect damages by integrating these local damage solutions, and an improved D-S theory is further presented to enhance the detection accuracy. The numerical and experimental examples show that the improved D-S theory has high detection accuracy and good performance.
Highlights
- An efficient method based on Dempster-Shafer theory and time domain model is proposed to detect crack damage.
- A cepstral metric conversion method based on the AR model is employed to obtain local damage solution.
- An autoregressive conditional heteroskedasticity conversion method based on ARCH model is presented to acquire another local damage solution.
- An improved probability quantity method based on different importance is presented to enhance the detection accuracy of the D-S theory.
1. Introduction
Vibration-based damage diagnosis and detection have received considerable attention in recent years [1]. The feasibility of vibration-based damage detection is that the damage usually changes the structural characteristics, such as stiffness, which are reflected in the measured vibration characteristics of the structure [2]. The vibration characteristics include measured frequency, mode shape and strain energy, which are often used in damage detection [3-5]. One category of vibration-based damage detection methods is the application of time domain analysis by constructing a time series model, which has been widely used in feature exaction to realize structural damage diagnosis and detection. Muślewski et al. [6] analyzed the vibration characteristics using vibration time histories in the time domain for propulsion systems of ships. Grządziela et al. [7] proposed a non-coaxiality identification method for shaft line systems of engines propelling the ships. Das et al. [8] made a comparative study among the different vibration-based damage detection methods: modal examination, local diagnostic approach, non-probabilistic methodology and time series method, and the results showed that the time series method results were more credible in damage detection than the other methods.
Generally, the time domain damage can be divided into two categories: linear damage and nonlinear damage. The linear damage got more attention and AR, ARX and ARMA models were widely applied in damage detection by fitting the response data of linear systems [9-12]. Zheng et al. [13] proposed a damage indicator based on the distance between ARMA models to detect structural damage including its location and severity. Xing et al. [14] utilized low-order AR models and cepstral metric to find damage locations. The principle of the method is that the distance between the models of damaged and undamaged states is correlated with the damage location information. Liu et al [15] proposed a non-probabilistic damage detection method, which employed the coefficient matrix of vector auto-regressive model to extract diagnosis elements and used Mahalanobis distance of these diagnosis elements to detect damages. Mei et al. [12] presented a substructure-based damage identification method to find damage locations and severity, and autoregressive moving average with exogenous variables model residual was utilized to correct the damage indicator.
Most of the damages in engineering structures actually possesses nonlinear characteristic, such as fatigue cracks that open and close due to dynamic loading. Although some methods and theories have been utilized for structural nonlinear damage detection [16-18], there are no damage detection methods with high reliability and sufficient research depth. The ARCH model was proposed by Engle [19], and subsequently was studied and applied by many researchers in the field of economics and finance. Pham et al [20] used a hybrid ARMA/GARCH model to diagnose the machine health state based on vibration signals. Chen et al. [21] also utilized the hybrid ARMA/GARCH model to diagnose the nonlinear damage of a three-storey structure and compared this model with the linear ARMA model. Yu et al. [22] presented a combination method based on the time domain model and statistical moments of structural responses to extract nonlinear damage information. Cheng et al [23] proposed the second order variance indicator based on the AR/ARCH model to identify nonlinear damage. These methods are mainly based on the degree of freedom (DOF) to identify structural damage locations, and it is still necessary to improve the identification reliability of nonlinear damage. Therefore, in this paper, a conversion technique is proposed to detect inter-storey stiffness damage and an improved D-S theory based on time domain model is presented to raise the identification reliability.
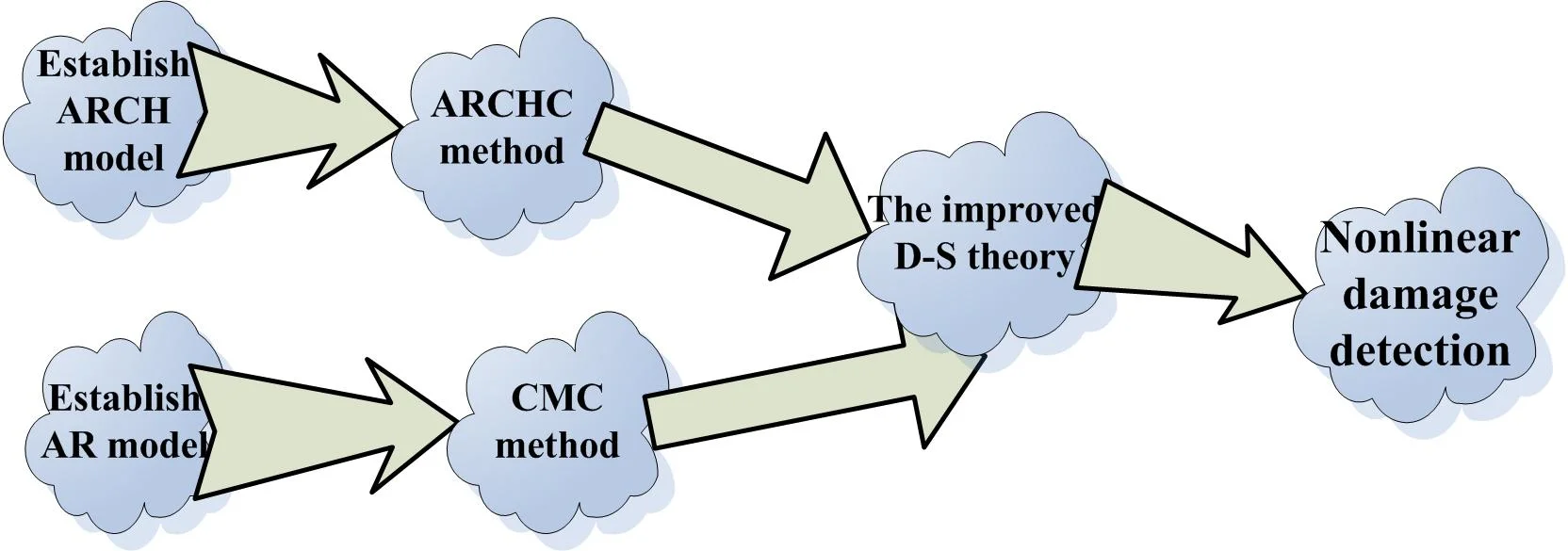
In this study, a nonlinear damage detection method based on the D-S theory and time domain model is proposed. First, the ARCH model is analyzed, and an autoregressive conditional heteroskedasticity conversion method is proposed. Then, the cepstral metric theory based on the autoregressive model is given, and a cepstral metric conversion method is described. Finally, the D-S theory is used to realize damage detection, and an improved strategy is presented. This paper consists of seven sections. In Section 2, the ARCH model is described, and the ARCHC method is proposed to localize nonlinear damage. In Section 3, the cepstral metric is analyzed, and the CMC method is given. The improved D-S theory and its application to damage detection are proposed in Section 4. Numerical and experimental examples are provided in Sections 5 and 6, respectively. Finally, Section 7 summarizes the conclusions.
2. ARCH model and ARCHC method
2.1. Nonlinear ARCH model
ARCH model is a volatility model that uses observed values of returns or residuals as volatility shocks. The basic theory of ARCH model is: Let denote a discrete time series set and let denote the information set available at time . The prediction value at time can be acquired by using the conditional expectation . Thus, the prediction residual or error can be expressed as:
Then, the conditional variance at time can be written as:
The values of past squared errors can be used to form the conditional variance function as follows:
In general, the error can be acquired from measured nonlinear time series , and the conditional expectation can be obtained by an autoregressive analysis. Thus, the Eq. (1) can be written as:
where is a constant, is the autoregressive coefficient, and is the number of autoregressive order. Similarly, the conditional variance of past squared errors can be specified as a linear function as follows:
where and (1,…, ) are the parameters of ARCH model, is a zero-mean unit-variance white noise. The values of the parameters are constrained by , , , .
The first two constraints ensure that conditional variances are positive, and the third constraint ensures covariance stationarity.
It is necessary to determine the order of ARCH model and estimate model parameters. The maximum likelihood estimation method can be used for estimating the parameters of an ARCH model. Akaike information criterion (AIC) can be used to determine the order of ARCH model. It utilizes a function based on the likelihood to choose the best order. The mathematical form of AIC can be expressed as:
where is the value of likelihood function, and is the number of estimated parameters. AIC represents a trade-off between the log-likelihood value and the number of parameters. In practice, we prefer to select the models with smaller AIC values.
2.2. ARCHC method
Generally, the structural damage identification can be implemented by comparing some features of a structure in different states, (i.e., undamaged state and damaged state). The structural acceleration time series in the undamaged and damaged states must be acquired from simulated or experimental vibration structure. The main steps of ARCH model application to establish the damage index are summarized as follows:
(1) Acquire the acceleration time series data in undamaged state and damaged state, so that the acquired time series meet stationarity.
(2) Extract residual sequences from the above acceleration data, and check if the residual sequences have ARCH effects.
(3) Estimate model parameters and determine the order of ARCH models. And then construct the ARCH models using the residual sequences and in the undamaged and damaged states.
(4) Acquire the conditional variance sequences and of the residual sequences and in the undamaged and damaged states, and calculate the corresponding variance and .
(5) Establish autoregressive conditional heteroskedasticity conversion (ARCHC) method based on calculated values in the undamaged and damaged states to identify the nonlinear damage. The ARCHC method is described as follows:
For an -storey structure with nonlinear damage, the residual sequences of acceleration responses are no longer white noise processes, i.e., conditional variances sequences vary with time. The variance of conditional variances sequences is much greater than zero. On the other hand, for an undamaged structure, the conditional variance sequences are stable. Therefore, nonlinear damage can be diagnosed by using some methods based on the ARCH model. Here, the ARCHC method is proposed to directly identify damage locations. The damage probability value of the th stiffness storey is given by:
where:
When 1, . Thus, the bottom effect is considered. is the stiffness storey number of shear structure. The ARCHC method can directly identify structural nonlinear damage location or provide local decision information for the following fusion.
3. Cepstral metric and CMC method
3.1. Cepstral metric of AR model
Martin [24] proposed cepstral metric of ARMA models. Xing et al [14] further developed the Martin’s method and proposed cepstral metric of AR model. An autoregressive model can be written as:
where is the coefficient of AR model, is the order of AR model, and is a white noise time sequence. The cepstral metric of AR model is described as follows [14]:
where and are AR models before and after damage, respectively. and are the order of models and . and are the pole parameters of models and .
3.2. CMC method
In general, it is difficult to identify stiffness damage through the cepstral metric based on DOFs. Therefore, it is necessary to establish the damage detection method based on the stiffness storey. Here, the CMC method is proposed to directly identify damage locations. The damage probability value of the th stiffness storey can be written as:
where:
When 1, . Thus, the bottom effect is considered. The CMC method can directly identify structural damage location.
4. Improved D-S theory and its application to damage detection
4.1. D-S theory and its application to damage detection
Dempster-Shafer theory is an effective information fusion approach for combining multiple data sources [25]. It has been widely utilized in the fields of pattern recognition.
Let be a finite set including hypotheses. The set is the frame of discernment. Basic probability quantity of focal element should meet the following constraint:
where expresses the focal element or evidence. The sum of basic probability quantity is 1. Dempster’s combination rule is the key part of D-S theory, which can combine multi-source data. Here, two sets of data sources and are considered. Let and be basic probability quantity given by sources and , respectively. The combination rule can be written as:
where:
where and are focal elements. is conflict factor between the data sources and . The item () is utilized to compensate for probability loss caused by non-intersecting subsets. Thus, the generated probability quantity is normalized to one.
In this study, two different data sources, the residual time series data and autoregressive time series data of acceleration responses are applied to damage detection. The local decisions can be acquired by using ARCHC method and CMC method, respectively. Then, the basic D-S theory can be used to obtain the global solution and localize damages.
4.2. Improved D-S theory and its application to damage detection
Generally, different information sources shall have different importance or reliability, but the basic D-S theory uses the equal importance strategy to deal with the fusion problem. Therefore, an improved strategy, which considers the effect of different importance, is proposed.
Consider two information sources and with different importance. Let and be the basic probability quantity given by sources and and let and be the probability importance coefficients which are the probability importance degree of sources and , respectively. Here, has a higher importance degree than , i.e., . In addition, the probability importance coefficients should meet the following constraint:
The and could not be directly utilized as modified probability quantity of sources and . The reason is the or could not meet the probability condition that the sum is 1. Here, an improved probability quantity method based on different importance is given as follows:
The generated probability quantity and all meet the normalization condition. Then, Dempster’s combination rule can be used by:
where
If the importance degrees of sources and are equal (i.e., ), the improved D-S theory can automatically become basic D-S theory.
In this study, residual time series data and autoregressive time series data of acceleration response are considered as two sources. In general, the residual time series data contain more nonlinear information than autoregressive time series data. Therefore, residual time series data is the source and autoregressive time series data is the source . can be acquired by using the ARCHC method and can be obtained by using the CMC method. Nonlinear ARCH model of ARCHC method can perfectly deal with nonlinear signals. Therefore, for nonlinear damage problem, the probability importance coefficient of ARCHC method is greater than of CMC method. Probability importance coefficients can be acquired by the relative recognition rate of the damage detection method. Of course, the coefficients can also be obtained in practice.
5. Numerical examples
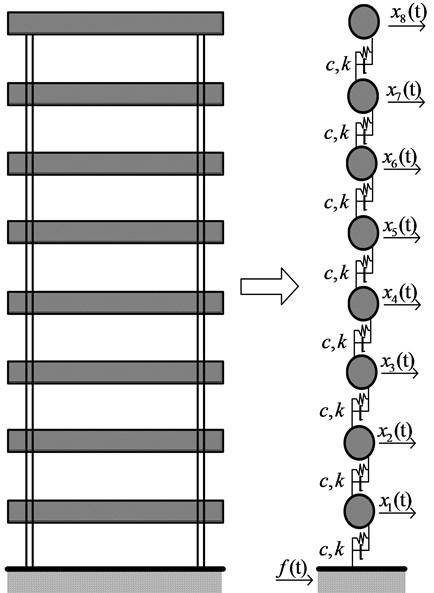
An eight-storey shear structure, which is shown in Fig. 1, is utilized to verify the effectiveness of the improved D-S theory. This structure can be simplified as an eight degree-of-freedom system. The parameters of the shear structure are: mass of every storey is 100 kg, lateral stiffness is 1 MN/m, and Rayleigh damping parameters and are 0.9842 and 0.00036. Nonlinear damage is simulated by means of the bilinear stiffness approach [26], which is given as follows:
where and are the displacement of the th and th storey, and denotes the th inter-storey stiffness. If 1, , expressing the displacement of structure basement. is damage coefficient. The bilinear stiffness approach is used to realize the simulation of breathing crack.
In this study, the damage coefficient has been assigned with two degrees of damage, i.e., 20 % and 30 %. Single damage occurs on the column from the 1st storey to 8th storey in turns. Thus, in total there are 16 damage scenarios. We can use the ‘stiffness storey’ to denote the inter-storey stiffness damage location. White noise which is filtered by Butterworth low-pass filter has the similar features as wind load or small earthquake. Therefore, the filtered white noise data is utilized as excitation loads, and the Wilson- method is adopted for calculating structural response. In addition, the disturbance of measurement noise cannot be ignored. Random noise, whose amplitude is adjusted to the same level as structural response, is added into the acceleration response time series as measurement noise. Thus, the acceleration time series with measurement noise can be written as:
where is acceleration time series with measurement noise, is acceleration time series calculated by the Wilson- method, is noise level, and is a random noise which amplitude has been adjusted to the same level as structural response. The noise level is 5 %.
Fig. 1Eight-storey shear structure
The ARCHC and CMC methods are utilized for damage detection. For the ARCHC method, the order of ARCH model should be determined. AIC is used for order determination of ARCH model, and the maximum likelihood estimation method is adopted for parameter estimation. Here, the acquired order of ARCH model is 5. For the CMC method, the Xing’s method [14] is used to obtain the order of AR model. The literature [14] already described the order determination method of AR model in detail. For the D-S theory, residual time series data is considered as source and autoregressive time series data is considered as source . So can be acquired by using the ARCHC method and can be obtained by using the CMC method. Then, the basic D-S theory and improved D-S theory can be utilized to realize damage detection. For the improved D-S theory, the probability importance coefficients and are 0.7 and 0.3, respectively.
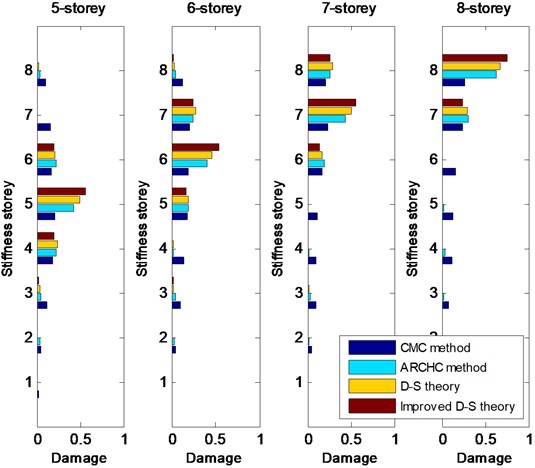
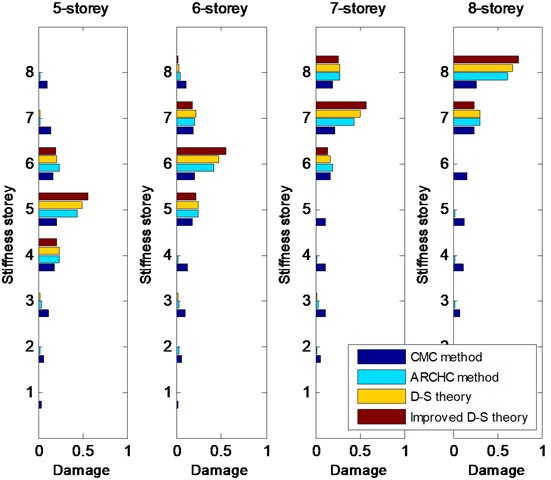
First, 20 % damage is considered. Single damage with 20 % stiffness reduction occurs from the 1st to 8th storey in turns. The CMC method, ARCHC method, D-S theory (or basic D-S theory) and improved D-S theory are applied for damage detection. The greater the calculation value of stiffness storey is, the higher the probability of damage is. The detection results from the 1st storey to the 8th storey with 20 % damage are shown in Figs. 2 and 3. From Figs. 2 and 3, it can be observed that the two methods based on the D-S theory exhibit better results than the CMC and ARCHC methods, except for the 1st storey. For the 1st-storey damage, the value of basic D-S theory is lower than that of ARCHC method, but the result of improved D-S theory is still higher than that of ARCHC method. Of course, for nonlinear damage problem, the ARCHC method is better than the CMC method and the calculated results of the improved D-S theory are superior to those of the basic D-S theory. Therefore, the improved D-S theory is better than the other three methods.
Fig. 2Detection results from the 1st-storey to 4th-storey damage with 20 % stiffness reduction
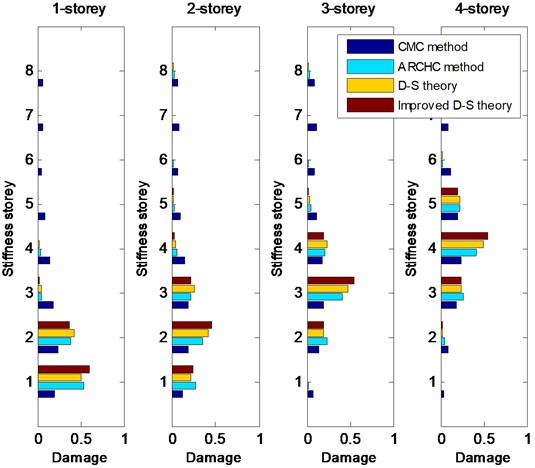
Fig. 3Detection results from the 5th-storey to 8th-storey damage with 20 % stiffness reduction
Then, 30 % damage is also considered. Single damage with 30 % stiffness reduction occurs from the 1st to 8th storey in turns. The CMC method, ARCHC method, D-S theory and improved D-S theory are used to realize nonlinear damage detection. The detection results from the 1st storey to the 8th storey with 30 % damage are depicted in Fig. 4 and 5. From Figs. 4 and 5, it can be seen that the two methods based on the D-S theory exhibit better results than both the CMC method and ARCHC method, except for the 1st storey. For the 1st-storey damage, the result of the basic D-S theory is inferior to that of the ARCHC method, but the result of improved D-S theory is obviously better than that of the ARCHC method. Therefore, the improved D-S theory is the best one among the four damage detection methods.
Fig. 4Detection results from the 1st-storey to 4th-storey damage with 30 % stiffness reduction
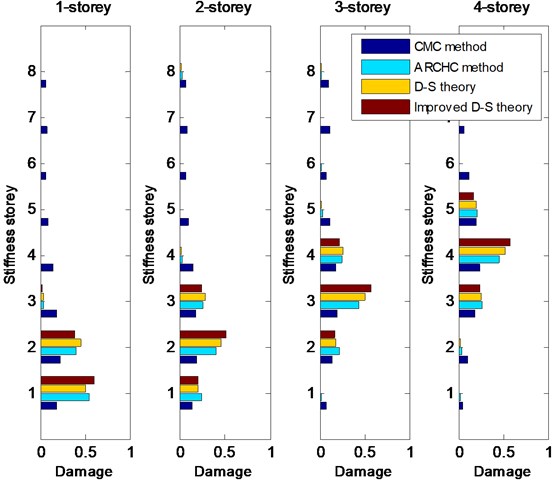
Fig. 5Detection results from the 5th-storey to 8th-storey damage with 30 % stiffness reduction
For nonlinear damage problem, the CMC method utilizes autoregressive time series data to identify damage, and the ARCHC method mainly utilizes residual time series data to identify damage. In general, the residual time series data contains more nonlinear information than autoregressive time series data. Therefore, the identification results of the ARCHC method are better than those of CMC method. Then, D-S theory is applied to further improve the identification results.
6. Experimental examples
A three-storey frame structure is utilized to verify the proposed method. The experimental frame structure with sensors is shown in Fig. 6 [27]. Nonlinear damage is modeled by a mechanism constituted of a bumper and a center column, which are used to generate nonlinear characteristic such as breathing crack prediction. The mechanism simulates the opening or closing of crack due to dynamic loads. The distance between the tip of the center column and the bumper is adjustable. In general, the greater the gap distance is, the weaker the nonlinear damage degree becomes. Therefore, in the experiment, nonlinear damage degree can be changed through adjusting the gap distance.
Fig. 6Three-storey frame

a) Three-storey frame

b) Adjustable bumper and suspended column
Table 1Sensor channels and parameters
Channel Number | Transducer | Reference | Nominal Sensitivity |
Channel 1 | Load cell | PCB 208 C03 SN 22569 | 2.2 mV/N |
Channel 2 | Accelerometer | PCB 336C SN 10099 | 1000 mV/g |
Channel 3 | Accelerometer | PCB 336C SN 10120 | 1000 mV/g |
Channel 4 | Accelerometer | PCB 336C SN 9916 | 1000 mV/g |
Channel 5 | Accelerometer | PCB 336C SN 10100 | 1000 mV/g |
Table 2Damaged states of three-storey frame structure
Damaged states | Description |
State 1 | Gap (0.05 mm) |
State 2 | Gap (0.10 mm) |
State 3 | Gap (0.13 mm) |
State 4 | Gap (0.15 mm) |
State 5 | Gap (0.20 mm) (weak nonlinearity) |
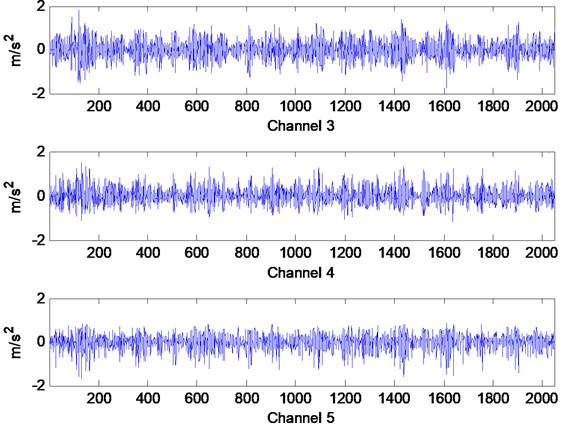
Accelerometers are installed on each floor including the bottom floor to record the time domain acceleration responses. The sensor channels and parameters are depicted in Table 1. The acceleration responses of the 1st storey, 2nd storey and 3rd storey of the structure are the measured data of Channels 3, 4 and 5. The damaged states are listed in Table 2. The greater the gap distance is, the weaker the nonlinear damage degree becomes. If the gap distance is great enough, the bumper will not contact the center column and nonlinear characteristic caused by stiffness change will disappear. The acceleration responses in undamaged state are depicted in Fig. 7, and the acceleration responses in damaged state 1 are depicted in Fig. 8. It can be seen that their response curves are apparently different.
Fig. 7Acceleration responses in undamaged State
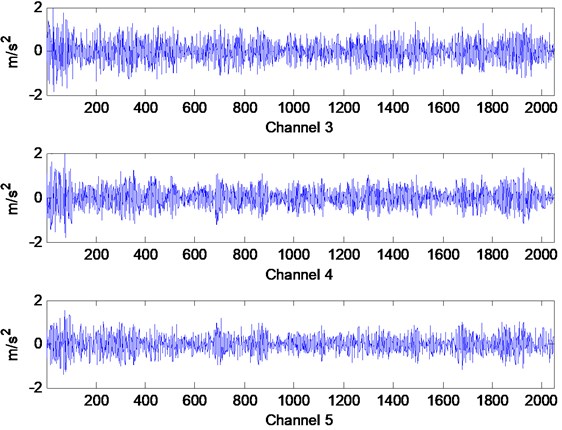
Fig. 8Acceleration responses in damaged State 1
Then, the order of time series model should be determined. Akaike information criterion is utilized to determine the order of ARCH model, and the maximum likelihood estimation method is adopted for parameter estimation. Here, the acquired order of ARCH model is 5. For the CMC method, the Xing’s method [14] is utilized to obtain the order of AR model. The order of AR model is 30. For the D-S theory, residual time series data is considered as source , and autoregressive time series data is considered as source . And can be acquired by using the ARCHC method, and can be obtained by using the CMC method. Then, the basic D-S theory and improved D-S theory can be used to detect structural damage. For the improved D-S theory, the probability importance coefficients and are 0.7 and 0.3, respectively.
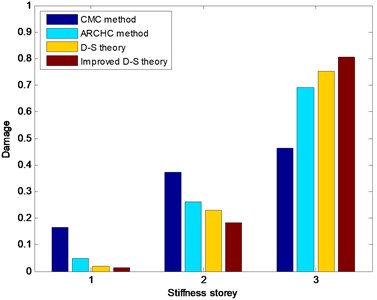
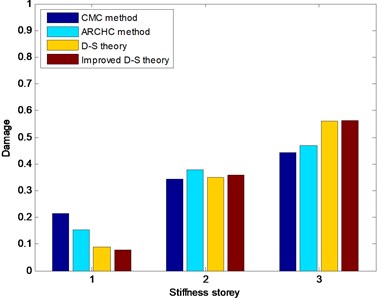
For damaged state 1, measured acceleration response signals are utilized to realize nonlinear damage detection. The third stiffness storey is the damaged location. The CMC method, ARCHC method, D-S theory (or basic D-S theory) and improved D-S theory are used to identify the structural damage location. The detection results for damaged state 1 are depicted in Fig. 9. From Fig. 9, it can be seen that all four methods possess the capacity of nonlinear damage detection. The two methods based on the D-S theory have relatively higher values than the CMC and ARCHC methods do for the damaged third storey. The reason is that the methods based on the D-S theory combine multiple source information. In addition, the calculated value of the improved D-S theory is higher than that of the basic D-S theory for the damaged third storey. Therefore, the improved D-S theory is the best one among all four damage detection methods.
Fig. 9Nonlinear damage detection results in damaged State 1
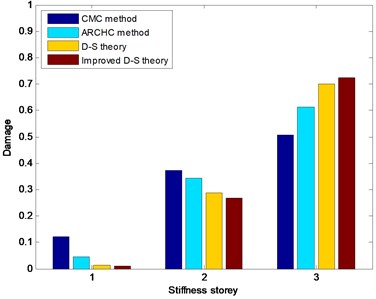
For damaged states 2-4, the damage is located in the third stiffness storey. The CMC method, ARCHC method, basic D-S theory and improved D-S theory are also utilized to detect structural damage location. The damage detection results with stiffness storey are depicted in Figs. 10-12. From Figs. 10-12, it can be seen that the two methods based on the D-S theory exhibit better results than both CMC method and ARCHC method do. In addition, the calculated value of the improved D-S theory is obviously higher than those of the other three methods for the damaged third storey. Although the other three methods can also approximately find the damage location, the improved D-S theory is obviously superior to the other three methods.
Fig. 10Nonlinear damage detection results in damaged State 2
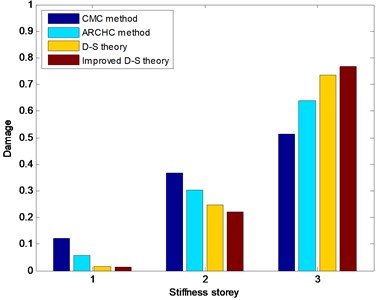
Fig. 11Nonlinear damage detection results in damaged State 3
Generally, the greater the gap distance is, the weaker the nonlinear damage degree becomes. Therefore, the damaged state 5 can be considered as a weak nonlinearity problem. For damaged state 5, the damage detection results are shown in Fig. 13. For the weak nonlinearity problem, the results of CMC and ARCHC methods are not good enough, and the nonlinear identification results of D-S theory are still superior to those of both CMC method and ARCHC method. The value of improved D-S theory is slightly higher than that of the basic D-S theory for the damaged third storey. Therefore, the improved D-S theory is still the best one among the four methods for the weak nonlinearity damage problem.
From numerical and experimental examples, for the nonlinear damage problem with measured error, the CMC method, ARCHC method, basic D-S theory and improved D-S theory have the capacity of detecting the damage location. The ARCHC method based on the ARCH model is better than the CMC method based on the cepstral metric and AR model. The detection results of two D-S theories are superior to those of both CMC method and ARCHC method. The reason is that the D-S theory integrates the damage information of two sources. In addition, the results of improved D-S theory are better than those of the basic D-S theory. So, it is obvious that the improved D-S theory is the best one among the four methods.
Fig. 12Nonlinear damage detection results in damaged State 4
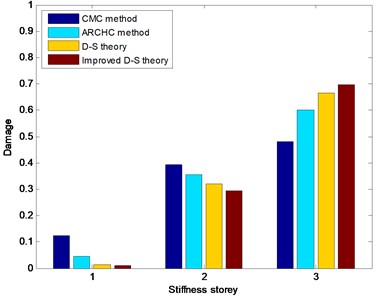
Fig. 13Nonlinear damage detection results in damaged State 5 (weak nonlinearity)
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
7. Conclusions
In this study, an improved D-S theory based on the time series model has been proposed to raise the detection accuracy of nonlinear damage. First, acceleration responses in the undamaged and damaged states are measured by using accelerometers. Then, acceleration responses are utilized to establish an AR model and residual time series of acceleration responses are used to establish an ARCH model. The CMC method based on the AR model is proposed to obtain local damage solution, and the ARCHC method based on the ARCH model is also proposed to acquire another local damage solution. Finally, the D-S theory is applied to damage detection by integrating these local damage solutions from the ARCHC and CMC methods. An improved D-S theory is further presented to enhance the detection accuracy. The main advantage of the improved D-S theory is that the proposed theory can effectively solve the problem that different information sources have different importance. By taking into account the results of simulation and experiment, the following conclusions can be drawn: (1) For the nonlinear damage problem, the ARCHC method based on the ARCH model is better than the CMC method based on the AR model. (2) The detection results of the improved D-S theory are not only superior to those of the basic D-S theory, but also better than those of the ARCHC and CMC methods. In a word, the improved D-S theory exhibits better performance and higher accuracy than other methods.
References
-
Sarrafi A., Mao Z., Niezrecki C., et al. Vibration-based damage detection in wind turbine blades using phase-based motion estimation and motion magnification. Journal of Sound and Vibration, Vol. 421, Issue 12, 2018, p. 300-318.
-
Li P. J., Xu D. W., Zhang J. Probability-based structural health monitoring through Markov chain Monte Carlo sampling. International Journal of Structural Stability and Dynamics, Vol. 16, Issue 7, 2016, p. 1550039.
-
Xu Y., Qian Y., Chen J., et al. Probability-based damage detection using model updating with efficient uncertainty propagation. Mechanical Systems and Signal Processing, Vol. 60, Issue 8, 2015, p. 958-970.
-
Tatar A., Niousha A., Rofooei F. R. Damage detection in existing reinforced concrete building using forced vibration test based on mode shape data. Journal of Civil Structural Health Monitoring, Vol. 7, Issue 1, 2017, p. 123-135.
-
Guo H. Y., Yuan H. F., Huang Q. Structural damage identification based on gray cloud rule generator algorithm. Advances in Mechanical Engineering, Vol. 11, Issue 1, 2019, https://doi.org/10.1177/1687814018819904.
-
Muślewski L., Pająk M., Grządziela A., et al. Analysis of vibration time histories in the time domain for propulsion systems of minesweepers. Journal of Vibroengineering, Vol. 17, Issue 3, 2015, p. 1309-1316.
-
Grządziela A., Musiał J., Muślewski L., et al. A method for identification of non-coaxiality in engine shaft lines of a selected type of naval ships. Polish Maritime Research, Vol. 22, Issue 1, 2015, p. 65-71.
-
Das S., Saha P., Patro S. K. Vibration-based damage detection techniques used for health monitoring of structures: a review. Journal of Civil Structural Health Monitoring, Vol. 6, Issue 3, 2016, p. 477-507.
-
Eloi F., Joaquim F., Gyuhae P., et al. Influence of the autoregressive model order on damage detection. Computer – Aided Civil and Infrastructure Engineering, Vol. 26, Issue 3, 2011, p. 225-238.
-
Bernal D., Zonta D., Pozzi M. ARX residuals in damage detection. Structural Control and Health Monitoring, Vol. 19, Issue 4, 2012, p. 535-547.
-
Bao C., Hao H., Li Z. X. Integrated ARMA model method for damage detection of subsea pipeline system. Engineering Structures, Vol. 48, Issue 3, 2013, p. 176-192.
-
Mei L., Mita A., Zhou J. An improved substructural damage detection approach of shear structure based on ARMAX model residual. Structural Control and Health Monitoring, Vol. 23, Issue 2, 2016, p. 218-236.
-
Zheng H., Mita A. Damage indicator defined as the distance between ARMA models for structural health monitoring. Structural Control and Health Monitoring, Vol. 15, Issue 7, 2008, p. 992-1005.
-
Xing Z., Mita A. Locating the damaged storey of a building using distance measures of low-order AR models. Smart Structures and Systems, Vol. 6, Issue 9, 2010, p. 991-1005.
-
Liu G., Mao Z., Luo J. Damage detection with interval analysis for uncertainties quantification. International Conference on Performance-based and Life-cycle Structural Engineering, Queensland, Australia, 2015, p. 272-281.
-
Prawin J., Rao A. R. M. Nonlinear structural damage detection based on adaptive Volterra filter model. International Journal of Structural Stability and Dynamics, Vol. 18, Issue 2, 2018, p. 1871003.
-
Ebrahimian H., Astroza R., Conte J. P. Nonlinear finite element model updating for damage identification of civil structures using batch Bayesian estimation. Mechanical Systems and Signal Processing, Vol. 84, Issue 1, 2017, p. 194-222.
-
Farrar C. R., Worden K., Todd M. D., et al. Nonlinear System Identification for Damage Detection. Technical Report, Los Alamos National Laboratory (LANL), Los Alamos, 2007.
-
Engle R. F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica, Vol. 50, Issue 4, 1982, p. 987-1007.
-
Pham H. T., Yang B. S. Estimation and forecasting of machine health condition using ARMA/GARCH model. Mechanical Systems and Signal Processing, Vol. 24, Issue 2, 2010, p. 546-558.
-
Chen L. J., Yu L. Structural nonlinear damage identification algorithm based on time series ARMA/GARCH model. Advances in Structural Engineering, Vol. 16, Issue 9, 2013, p. 1597-1609.
-
Yu L., Zhu J. H. Nonlinear damage detection using higher statistical moments of structural responses. Structural Engineering and Mechanics, Vol. 54, Issue 2, 2015, p. 221-237.
-
Cheng J. J., Guo H. Y., Wang Y. S. Structural nonlinear damage detection method using AR/ARCH model. International Journal of Structural Stability and Dynamics, Vol. 17, Issue 8, 2017, p. 1750083.
-
Martin R. J. A metric for ARMA processes. IEEE Transactions on Signal Processing, Vol. 48, Issue 4, 2000, p. 1164-1170.
-
Sun L., Srivastava R. P., Mock T. J. An information systems security risk assessment model under the Dempster-Shafer theory of belief functions. Journal of Management Information Systems, Vol. 22, Issue 4, 2006, p. 109-142.
-
Rébillat M., Hajrya R., Mechbal N. Nonlinear structural damage detection based on cascade of Hammerstein models. Mechanical Systems and Signal Processing, Vol. 48, Issue 1, 2014, p. 247-259.
-
Figueiredo E., Park G., Figueiras J., et al. Structural Health Monitoring Algorithm Comparisons Using Standard Data Sets. Report No.: LA-14393, Los Alamos National Laboratory (LANL), Los Alamos, United States, 2009.
Cited by
About this article
This work was supported by the National Natural Science Foundation of China (Grant No. 51578094).
