Abstract
The geometric irregularities present inside a structure results in an improper stress distribution caused during manufacturing, which not only affects the strength of the component but also its vibrational behaviour when operated in a fluctuating environment. The emphasis of this paper is to evaluate the stress behavioral characteristics of plates with different cutout shapes. Two different loading conditions with three different types of plates made of Mild Steel are used for this analysis. From the present investigation, it may be concluded that where the max stress occurs. The methodology adopted in this research work is based on the numerical technique of finite element method, which uses SOLID 185 in ANSYS 19.1 solver. For further analysis, the obtained results are validated with previous literature works which were found satisfactory when related to the present study. It may be noted that FEM provides good insight for the determination of stress and deflection, with different parameters.
1. Introduction
Plates are the structural members which are generally manufactured for fabrication purpose. The presence of cut out in plates is especially carried out for inserting bolt and nuts. In order to reduce the weight of the structural members, these cutouts play a crucial role. The stress concentration caused due to cutouts with improper alignment in fastening may lead to high stresses, even sometimes it may cause the failure of the structural members. In order to assess the failure of these components stated in terms of deflection and stresses finite element analysis, a numerical method used as an important tool for finding out the stress behaviour characteristics.
2. Literature review
Active researchers in the field of structural engineering carried out enormous work on stress analysis of plates with various configurations. The stress analysis of a rectangular plate with a central hole was carried out by Dhanjal [1]. Using finite element method from the research they observed that the value of SEF tends to increase whereas the value of vonMises stress tends to decrease with an increase in / ratio. The calculation of stresses and deflection for a rectangular plate with central hole subjected to transverse loading was done by Jain [2]. He considered both isotropic and orthotropic materials for his analysis. Ahmed [3] used tensile load for assessing the deflection and stresses over circular plate made of isotropic material and orthotropic materials. He used FEM based Ansys tool for performing the analysis. The stress analysis of composite plates with varying cutouts was carried out by Riyah and Ahmed [4]. Various orientation angles in the ply sequence are experimented in their analysis. The Elasto-plastic stress analysis with varying boundary conditions was done by Sayman and Askoy [5]. They used clamped free and simply supported boundary conditions for metal matrix laminated plates positioned with a central hole. The stress analysis has been carried out based on classical lamination plate theory. Using finite element method as a basis the determination of Von misses and deflection for a rectangular plate with elliptical home was carried out by Dheeraj and Singh [6].With the plate dimensions remaining the same and varying the diameter of the hole to the width of the plate the effect on orientation angle on shear, axial stresses and their corresponding deflections for the clamped free boundary conditions are examined. Shaik and Mirzana [7] performed the static analysis for a plate with a central hole with different materials. Mekalke [8] investigated the stress analysis of a plate with a central hole subjected to uniform stress distribution. From his examination, he determined the deviation in the results by varying the mesh sizes and types. Brahmbhatt [9] analyzed the rectangular plate with an elliptical hole for stress analysis. From the results, he concluded that the stress intensity factor gives less error for the lower values of aspect ratio.
3. Problem definition
For present work, various shapes of plates with mild steel as the base material is used for calculating the induced stresses and deformations produced due to the uniformly distributed pressure. Also, the effect of various cutout shapes of rectangular, square, triangular, circular, elliptical with two different boundary conditions clamped free and simply supported conditions have been analyzed. The stress concentration factor for a rectangular plate made of Magnesium alloy and Polyethylene material subjected to clamped boundary conditions are determined, taken from the literature. The material properties are shown in Table 1and Table 2 gives the dimensions of the plate with cutouts.
Table 1Properties of rectangular plate
Properties | Mild Steel |
Young’s modulus | 205 GPa |
Poisson’s ratio | 0.35 |
Density | 7850 Kg/m3 |
Table 2Dimensions of plates with various cutout dimensions
Plate type | No cutout | Cutout shape | ||||
Rectangular | Square | Elliptical | Circular | Triangular | ||
Rectangular | 500×300×25 mm | 100×50 | 100×100 | 100×50 | 75 | 100×100 |
Square | 500×500×25 mm | 100×50 | 100×100 | 100×50 | 75 | 100×100 |
4. Results and discussions
The stress analysis of a rectangular and square plate with a case of clamped free and simply supported boundary conditions has been studied in the present study for which the deflections and corresponding stresses are obtained. The effects of different cutouts positioned centrally in these plates are observed. The following observations are made to meet the desired result is as follows:
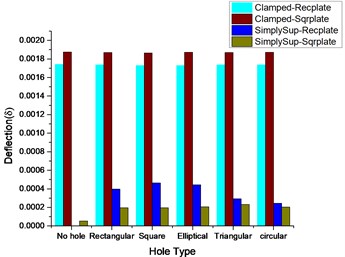
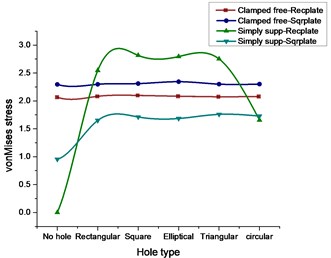
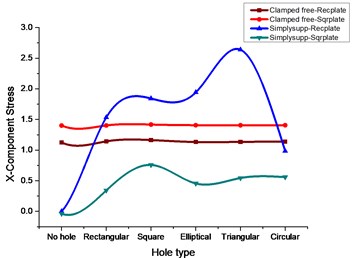
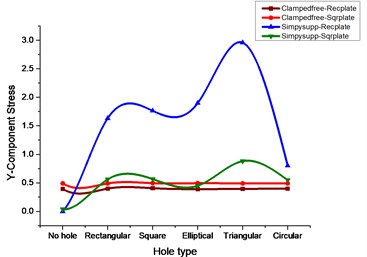
1) Table 3 gives the values of stress and its corresponding deflections for a rectangular plate subjected to clamped free boundary conditions. From the results, it can be observed that the deformation value will be same for all the cutouts with a marginal difference, whereas the values of vonMises stress, Principal stresses, and Componential stresses are more for a rectangular plate with the square type of cutout.
2) From Table 4 with the change of plate from rectangular to square type applying the same clamped free boundary condition, the value of stress components is more for the square type of cutout followed by the elliptical type.
3) Table 5 signifies that with the change of boundary condition from clamped free to simply supported type applied to rectangular plate the deformation and maximum stress are more for the square type of cutout whereas components stress and principal stresses are more for triangular type cutout.
4) From Table 6 the square plate with simply supported type boundary condition it makes clear that the value of deformation and maximum stress are more for the square type of cutout whereas components stress and principal stresses are more for triangular type cutout.
Table 3Stress analysis for a clamped-free rectangular plate with various central cutouts
Parameters | No hole | Rectangular | Square | Elliptical | Triangular | Circular |
Deformation () | 0.001741 | 0.001738 | 0.00173 | 0.00173 | 0.001736 | 0.001736 |
-component | 1.12474 | 1.14322 | 1.16374 | 1.132243 | 1.13419 | 1.13977 |
-component | 0.39364 | 0.39957 | 0.40707 | 0.38998 | 0.395145 | 0.397935 |
1st principal stress | 1.8639 | 1.88265 | 1.90387 | 1.89552 | 1.87297 | 1.87908 |
2nd principal stress | 0 | 0 | 0 | 0 | 0 | 0 |
3rd principal stress | –0.345524 | –0.34017 | –0.333056 | –0.33345 | –0.343583 | –0.341373 |
Von Mises stress | 2.05853 | 2.07377 | 2.09089 | 2.07647 | 2.06656 | 2.07098 |
Table 4Stress analysis for clamped-free square plate with various central cutouts
Parameters | No hole | Rectangular | Square | Elliptical | Triangular | Circular |
Deformation () | 0.001874 | 0.001870 | 0.001865 | 0.0018725 | 0.001870 | 0.001871 |
-component | 1.40021 | 1.40209 | 1.4169 | 1.405699 | 1.40483 | 1.40596 |
-component | 0.490073 | 0.489927 | 0.495154 | 0.494545 | 0.490549 | 0.490547 |
1st principal stress | 2.15326 | 2.1551 | 2.17038 | 2.15886 | 2.15776 | 2.15884 |
2nd principal stress | 0 | 0 | 0 | 0 | 0 | 0 |
3rd principal stress | 2.41624 | –0.263085 | –0.2584 | –0.275885 | –0.262383 | –0.262327 |
Von Mises stress | 2.29607 | 2.29797 | 2.31049 | 2.344021 | 2.3002 | 2.30124 |
Table 5Stress analysis for simply supported rectangular plate with various central cutouts
Parameters | No hole | Rectangular | Square | Elliptical | Triangular | Circular |
Deformation () | 0 | 0.398e-03 | 0.463e-03 | 0.443e-03 | 0.292e-03 | 0.245e-03 |
-component | 0 | 1.53381 | 1.84204 | 1.94223 | 2.63823 | 0.984279 |
-component | 0 | 1.63257 | 1.76389 | 1.89893 | 2.95788 | 0.800575 |
1st principal stress | 0 | 2.72194 | 3.03275 | 3.02547 | 3.12267 | 0.986324 |
2nd principal stress | 0 | 0.400506 | 0.565484 | 0.6548 | 1.07301 | –0.05275 |
3rd principal stress | 0 | 0 | –1.1086 | 0 | –1.15961 | –0.345e-04 |
Von Mises stress | 0 | 2.5461 | 2.81564 | 2.79521 | 2.7529 | 1.65708 |
Table 6Stress analysis for simply supported square plate with various central cutouts
Parameters | No hole | Rectangular | Square | Elliptical | Triangular | Circular |
Deformation () | 0.537e-04 | 0.197e-03 | 0.195e-03 | 0.206e-03 | 0.231e-03 | 0.203e-03 |
-component | –0.037595 | 0.342494 | 0.758062 | 0.455877 | 0.544554 | 0.558754 |
-component | 0.037612 | 0.561612 | 0.566197 | 0.448755 | 0.881004 | 0.548757 |
1st principal stress | 0.083589 | 0.905531 | 1.24483 | 0.915531 | 0.95565 | 1.14435 |
2nd principal stress | –0.037595 | –0.036444 | –0.048254 | –0.034557 | –0.035774 | –0.035567 |
3rd principal stress | –0.187378 | –0.181914 | –0.182976 | –0.181759 | –0.179844 | –0.187944 |
Von Mises stress | 0.954199 | 1.65003 | 1.71198 | 1.684454 | 1.75966 | 1.728855 |
Fig. 1Deflection and vonMises comparison for rectangular and square plates for various cutouts
a)
b)
Fig. 2X, Y-component stress comparison for rectangular and square plates for various cutouts
a)
b)
Fig. 3I, II-Principal stress comparison for rectangular and square plates for various cutouts
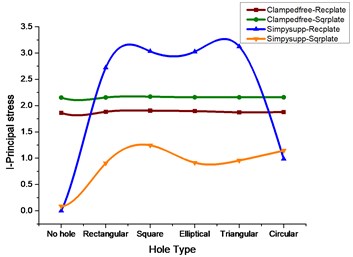
a)
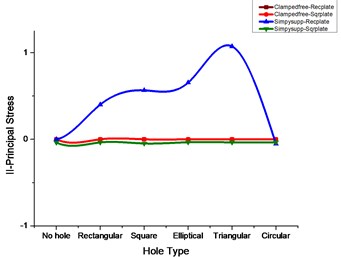
b)
Fig. 4III-Principal stress comparison for rectangular and square plates for various cutouts
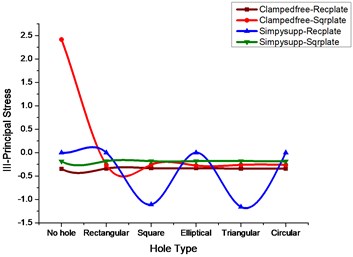
5. Conclusions
The stress analysis of plates with a centrally positioned cutout is of practical importance in designing the engineering structures, closed form of solutions for different types of cutouts for plates are not generally available, for these types of cutouts the solutions are determined either experimentally or numerically using finite element methods. This study has presented a numerical solution for various stresses i.e. rectangular and square plates with specially shaped cutouts. The stress analysis of isotropic material based rectangular and square plates with a variety of centrally located cutouts was investigated. Numerical studies were conducted to investigate the effects of variation on cutout shape, geometries in the location and the value of the maximum stress in the plate under uniformly distributed pressure. Two types of boundary conditions simply supported and clamped free is applied to the plates consisting of special cutout shape. The adapted numerical scheme can be used for evaluating the stress concentration and finding out the stress distribution in isotropic and laminated plates. The effect of cutout shape for static analysis of plates can significantly change by varying the material properties, cutout parameters.
References
-
Dhanjal S., Arora R. Stress analysis of a rectangular plate with circular hole using three dimensional finite element model. International Journal of Engineering, Business and Enterprise Applications (IJEBEA), Vol. 12, Issue 1, 2015, p. 77-80.
-
Jain N. K. Analysis of stress concentration and deflection in isotropic and orthotropic rectangular plates with central circular hole under transverse static loading. International Journal of Mechanical and Mechatronics Engineering, Vol. 3, Issue 12, 2009, p. 1513-1519.
-
Ahmed M. A. Comparison the stresses and deflections of anisotropic and orthotropic rectangular plates with a central circular hole under a tension load. AL Rafdain Engineering Journal, Vol. 20, Issue 4, 2011, p. 137-153.
-
Riyah N. K., Ahmed N. E. Stress analysis of composite plates with different types of cutouts. Anbar Journal for Engineering Sciences, Vol. 2, Issue 1, 2009, p. 11-29.
-
Sayman O., Aksoy S. Elastic-plastic stress analysis of simply supported and clamped aluminum metal-matrix laminated plates with a hole. Composite Structures, Vol. 53, 2001, p. 355-364.
-
Gunwant D., Singh J. P. Stress and displacement analysis of a rectangular plate with a central elliptical hole. International Journal of Engineering and Innovative Technology, Vol. 3, Issue 3, 2013, p. 387-392.
-
Shaik S., Mirzana I. M. Stress concentration of rectangular plate with a hole made with composite material using finite element analysis. IOSR Journal of Mechanical and Civil Engineering. (IOSR-JMCE), Vol. 13, Issue 4, 2016, https://doi.org/10.9790/1684-13040740105.
-
Mekalke G. C., Kavade M. V., Deshpande S. S. Analysis of a plate with a circular hole by FEM. IOSR Journal of Mechanical and Civil Engineering (IOSR-JMCE), Vol. 1, Issue 5, 2012, p. 25-30.
-
Brahmbhatt D., Brahmbhatt K., Patel D. Stress concentration factor converts into stress intensity factor using ANSYS. European Journal of Advances in Engineering and Technology, Vol. 2, Issue 1, 2015, p. 46-49.
