Abstract
In this paper, numerical analysis for free vibration of simply supported thin rectangular plates has been simulated using Ansys. The vibration of plate follows Kirchhoff plate theory. The natural frequency calculated using Ansys has been compared with Levy type solution results available in the literature. It is observed that the natural frequencies of the simply supported rectangular plate is in close agreement with exact solution results as reported in literature.
1. Introduction
A thin plate is a solid structural body where the thickeness of the plate is small as compared to other two dimensions.
In modern science explorations, rectangular thin plate structures are used in aerospace industries, mechanical, automotive sectors, civil and marine industries etc. In the actual engineering environment, there are many external forces which cause vibrations in the thin plate structures. These forced vibrations are the cause of failure and damage to the engineering structures. To investigate the dynamic response due to forced vibration of the plate structure, natural frequencies and their mode shape estimations are very important. So, this paper is about the analysis of free vibrations of rectangular thin plates in simply supported condition using finite element with Ansys software.
Tanaka et al. [2] solved the free vibrations of elastic plates using integral equation process. Karunasena and Kitipornchai et al. [3] determined the free vibration analysis of deformable triangular element. Wu and Liu et al. [4] have been studied the new numerical solution technique called as differential cubature method for free vibration analysis of arbitrary shaped plates. Moon and Choi et al. [5] have formulated the transfer dynamic stiffness coefficient method for vibration analysis of frame structures. Myung [6] has developed the finite element transfer stiffness coefficient method for free vibration analysis of plate structures. The approach is based on the combination of the modelling techniques in FEM and the transfer technique of the stiffness coefficient in the transfer stiffness coefficient method. Kumar et al. [7] use dynamic stiffness method to extract natural frequency and mode shapes of thin plate. Piyush et al. [8] used Rayleigh-Ritz method to compute the natural frequencies of thin plate.
2. Methodology
The Kirchhoff plate theory is a two dimensional mathematical model that is used to determine the stresses and deformation in thin plates when they are subjected to force and moments.
The assumptions made in Kirchhoff plate theory are:
1) Straight lines normal to the mid surface remains straight after deformation.
2) The thickness of the plate does not change during a deformation.
3) Straight lines normal to the mid surface remain normal to the mid surface after deformation.
This theory is used to model the transverse vibration of the plate. According to Kirchhoff plate theory, the equations for the transverse vibration of plate is given by:
where is flexural rigidity:
The finite element method is used to calculate the natural frequency. The general equation of finite element for the transverse deflection of thin plate is given by:
where [] is the mass matrix, [] is stiffness matrix, is the nodal acceleration vector and is nodal displacement vector.
The analytical calculation of natural frequencies are also carried out using Eq. (4):
where – natural frequencies, – density, , – length and width of rectangular plate, – thickness of plate.
The material properties and dimensions that are considered for the analysis of simply supported rectangular plate are referred from Ramu et al. [1].
The material properties of rectangular plate are:
Material = Aluminium;
Young’s modulus 70×109 N/m2;
Density 2700 kg/m3;
Poisons ratio 0.3.
The dimensions of plate taken are:
Length of plate 600 mm;
Width of plate 400 mm;
Thickness 6.25 mm, 12.5 mm, 25 mm, 50 mm.
Fig. 1Dimensions of the rectangular plate
Finite element analysis formulation for rectangular element have four nodes. There are three degrees of freedom at each node, one is along the thickness of the plate and the other two are rotations along and directions. The solid rectangular plate is modelled in Ansys software and the size of the mesh is 1.e-002 m. The number of elements taken are 2400 and the number of nodes are 5002. The face meshing of the rectangular plate gives the solutions which are close agreement to the theoretical values.
The geometry of plate 600 mm×400 mm with varying thickness.
Fig. 2Finite element model of plate

3. Results and discussion
In this section, the first six natural frequencies and mode shapes of simply supported rectangular plates are estimated using Finite Element Method. The present natural frequencies results are compared with those available in literature and with exact solutions.
Tables 1-4 shows that the first six natural frequencies of thin rectangular plate. These results are nearly same as Ramu [1] and analytical solutions under different thickness of the plate.
Fig. 3First six mode shapes of simply supported rectangular plate
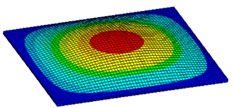
a) 1st mode shape
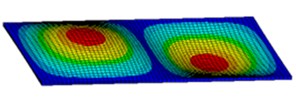
b) 2nd mode shape
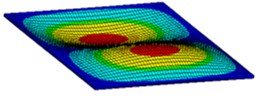
c) 3rd mode shape

d) 4th mode shape
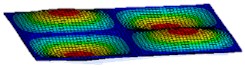
e) 5th mode shape
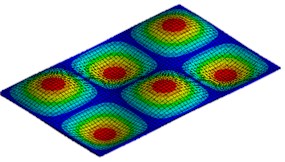
f) 6th mode shape
Table 1Comparison of the natural frequency parameter with analytical solution and Ramu [1] for simply supported rectangular plate with the thickeness of 6.25 mm
Results | Mode number | |||||
1 | 2 | 3 | 4 | 5 | 6 | |
Analytical | 136.56 | 262.75 | 420.41 | 472.96 | 546.53 | 756.73 |
Ramu [1] | 135.8 | 259.9 | 417.6 | 466.8 | 535.9 | 733.7 |
Present (FEA) | 136.92 | 263.27 | 422.27 | 474.53 | 547.86 | 758.07 |
Table 2Comparison of the natural frequency parameter with analytical solution and Ramu [1] for simply supported rectangular plate with the thickness of 12.5 mm
Results | Mode number | |||||
1 | 2 | 3 | 4 | 5 | 6 | |
Analytical | 273.12 | 525.51 | 840.82 | 945.92 | 1093.06 | 1513.477 |
Ramu [1] | 271.7 | 519.8 | 835.2 | 933.7 | 1071.9 | 1467.5 |
Present (FEA) | 272.17 | 522.27 | 833.59 | 940.3 | 1083.3 | 1493.7 |
Table 3Comparison of the natural frequency parameter with analytical solution and Ramu [1] for simply supported rectangular plate with the thickness of 25 mm
Results | Mode number | |||||
1 | 2 | 3 | 4 | 5 | 6 | |
Analytical | 546.25 | 1051.02 | 1681.64 | 1891.84 | 2186.13 | 3026.95 |
Ramu [1] | 543.5 | 1039.7 | 1670.5 | 1867.5 | 2143.7 | 2935.1 |
Present (FEA) | 535.26 | 1019.8 | 1634.9 | 1823.1 | 2088.3 | 2847.7 |
Table 4Comparison of the natural frequency parameter with analytical solution and Ramu [1] for simply supported rectangular plate with the thickness of 50 mm
Results | Mode number | |||||
1 | 2 | 3 | 4 | 5 | 6 | |
Analytical | 1092.51 | 2102.05 | 3363.28 | 3783.69 | 4372.26 | 6053.91 |
Ramu [1] | 1087 | 2079.4 | 3341 | 3735 | 4278.4 | 5870.2 |
Present (FEA) | 1024 | 1906.8 | 3008.8 | 3100.6 | 3316 | 3748.1 |
4. Conclusions
In this paper, numerical analysis for free vibration analysis of thin rectangular solid plate is carried out using Finite Element Method under simply supported condition with varying the thickness. It is found that those natural frequency results are quite close to the reported literatures. As the thickness of the rectangular plate increases, the values are not so close to the analytical values.
References
-
Ramu I., Mohanty S. C. Study on free vibration analysis of rectangular plate structures using finite element method. Procedia Engineering, Vol. 38, 2012, p. 2758-2766.
-
Tanaka M., Yamagiwa K., Miyazaki K., Ueda T. Free vibration analysis of elastic plate structures by boundary element method. Engineering Analysis, Vol. 5, Issue 4, 1988, p. 182-188.
-
Karunasena W., Kitipornchai S. Free vibrations of shear deformable general triangular plates. Journal of Sound and Vibration, Vol. 199, Issue 5, 1997, p. 595613.
-
Wu L., Liu J. Free vibration analysis of arbitrary shaped thick plates by differential cubature method. International Journal of Mechanical Sciences, Vol. 47, 2005, p. 6381.
-
Moon D. H., Choi M. S. Vibration analysis for frame structures using transfer of dynamic stiffness coefficient. Journal of Sound and Vibration, Vol. 234, Issue 5, 2000, p. 725736.
-
Myung Soo Choi Free vibration analysis of plate structures using finite element-transfer stiffness coefficient method. KSME International Journal, Vol. 17, Issue 6, 2003, p. 805-815.
-
Kumar S., Vinayak Ranjan, Jana P. Free vibration analysis of thin functionally graded rectangular plates using the dynamic stiffness method. Composite Structures, Vol. 197, 2018, p. 39-53.
-
Pratap Singh P., Azam M. S., Ranjan Vinayak Vibration analysis of a thin functionally graded plate having an out of plane material inhomogeneity resting on Winkler-Pasternak foundation under different combinations of boundary conditions. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018.
