Abstract
A non-ideal connection of mechanical assembly with linear assembling interface is firstly considered in the coupling dynamic stiffness identification by applying the second scheme of indirect inverse substructuring analysis. The experimental model of the mechanical assembly is designed, and the interface is then discretized equivalently as ideal point-coupling for testing the frequency response functions (FRFs) involved in the scheme. As the results of the experimental study, applying the scheme is verified to be feasible for the stiffness identification of a mechanical assembly with linear connection, and the identified stiffness approaches to be stable with increase of the number of discretized points.
1. Introduction
Complex electro-mechanical products are generally assembled by a number of parts or components in terms of design specifications. Conventional quality inspection of mechanical assembly is primarily concentrated on its ‘static quality’ criterions, such as tolerances and or size-coordination, [1, 2] etc. However, the dynamic quality of the products, e.g., vibration, noise and stability, is often contributed directly by the ‘dynamic quality’ of the mechanical assembly, which is supposed to be inspected supplementarily in estimating the assembly quality.
The dynamic characteristics of assembling interface or connecting parts dominates the dynamic quality of a mechanical assembly. Determining the characteristics or identifying the dynamic stiffness as one of the characteristics of mechanical connections or joints is always paid lots of attentions. For instances, Majid [3] used inverse conduction coupling to consider the model of mechanical joint as ‘point-mass connection’ and identified the dynamic characteristics of connection by combining tested frequency response functions (FRFs) with FEM; Targeting at the difficulty of modeling structural connecting dynamic property by pure theoretical analysis, Damjan and Miha [4] tried to identify the dynamic flexibility of beam with bolt-connections; Hwang [5] studied the parameter identification modeling of structural connections based on FRFs, and eliminated the low precision resulted from high sensitive modes, which avoids the defect of establishing the model of ‘mass-damping-stiffness’ matrices in modal analysis. Summarily, these theories or methods belong to “positive problem” by use of dynamic substructuring analysis, and need predetermined dynamic parameters, resulting in large amount of computations, complicated process, and thus both accuracy and efficiency are to be enhanced.
In view of the existing problems mentioned above, Lim proposed FRF-based inverse substructuring method [6] and applied to vibro-response analysis of vehicle system [7]. It belongs to the inverse issue of structural dynamic analysis – using tested FRF-spectra at system level to ‘inversely find’ the dynamic characteristics of substructures and their coupling interface(s) or connection(s). Either modal tests and computations or modification by statistical approaches are thus avoided. It is so-called ‘direct scheme of inverse substructuring analysis’, simply called ‘direct scheme’. Lu Guangqing applied it firstly to the dynamic characteristic analysis of transportation packaging systems [8] and computed the dynamic stiffness of the packaging unit-of-coupling [9]. In addition, the inverse substructuring analysis of mechanical assembly was also carried out [10], including using the coupling dynamic stiffness of the assembly [11] and eigenvalues of assembling matrix [12] as the quantitative criterions for dynamic quality estimation of a mechanical assembly, respectively. Considering testing operational limitation of the direct scheme in engineering application, five ‘indirect schemes of inverse substructuring analysis’, simply called ‘indirect scheme’) were established [13] to identify the coupling dynamic stiffness of mechanical assembly. In the literature, their theoretical completeness is validated by analytical simulations, the feasibility and effectiveness of the first indirect scheme were additionally verified by an experimental model of the mechanical assembly with “point-coupling” interface of connection.
Targeting at the second indirect scheme, this study designs an experimental model of mechanical assembly with linear connection, which is one of commonly-used non-ideal coupling interfaces. The connection of the model is equivalently discretized into a number of ‘point-couplings’ at first. Then, the feasibility of the scheme in identifying the coupling dynamic stiffness of the assembly with linear connection is verified by experimental study. This work is further to provide a basis for engineering application of the scheme.
2. The second indirect scheme identifying the coupling dynamic stiffness
A mechanical assembly system with discrete couplings can be analyzed by the equivalent model of two-level substructures, i.e., ‘substructure A-coupling connection-substructure B’, as shown in Fig. 1.
Fig. 1Two-level substructural model with discrete couplings
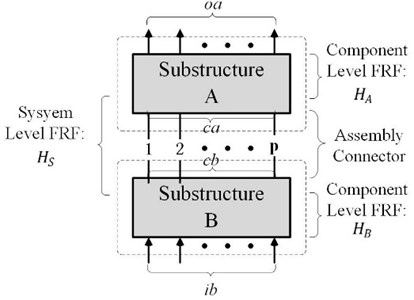
The two substructures A and B are considered as the two components of mechanical assembly respectively. Where, the discrete couplings are denoted by and , and the external input force of excitation on component B and the output response of dynamic displacement on component A are denoted by and . The FRF from the excitation to the response on the coupling system of assembly is denoted by , called FRF at system level, while the FRFs from excitations to responses on the non-coupling components A and B are denoted by and , respectively. And the coupling dynamic stiffness of the assembly is represented as . They are generally in form of a matrix.
In terms of substructural analysis, the FRF spectral matrices of the model before and after assembly have the following relations [7]:
where, –1 represents inverse operation of matrix, or or −1(), and is the coupling dynamic stiffness matrix. In terms of the equality of the entries on both sides of Eq. (1), if choosing the same numbers of (, ), (, ) and (, ), then five indirect schemes of inverse substructuring analysis for determining coupling dynamic stiffness of mechanical assembly can be derived [13], where, the second scheme is expressed as:
Eq. (3) shows that the difficulty of testing FRFs on the connection of assembly can be avoided. Its analytical completeness has been validated in literature [13]. Applying Eq. (3) to identify the stiffness of mechanical assembly needs 6 FRF-matrices totally, including that at component level before assembly, , , , and , and one at system level after assembly, , see Fig. 2.
Fig. 2The FRFs involved in the second indirect scheme
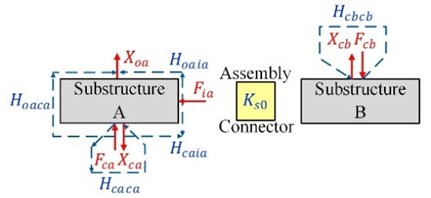
a) FRF at component level
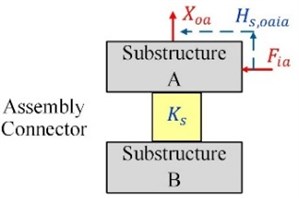
b) FRF at system level
3. Experimental model of mechanical assembly with linear connection
In order to verify the feasibility of applying the second indirect scheme to identify the coupling dynamic stiffness, of mechanical assembly, here designs an experimental model of mechanical assembly with linear connection, as shown in Fig. 3. Component A consists of two steel plates and welded together (size of : 120×300×10 mm3; size of 300×260×16 mm3), component B (steel plate with size of 300×260×10 mm3). Both are added different mass of blocks attached onto the plates by damping rubber cylindrical bars ( 35 mm). Component A is assembled through one lateral of plate , which is adhered onto the middle line of component B, in the form of linear connection.
All the FRF-entries involved in the second indirect scheme of Eq. (3) are tested by “point-viro-excitation to point-displacement-response” on the components with linear connection. Therefore, the coupling interface of the connection must be discretized to be equivalently to ‘point-to-point connections’. Consequently, the coupling interface of the linear connection in-between components A and B is divided into two, three, four, five and six segments. There are mono-, bi-, tri-, quad- and pent-coupled ‘point-to-point connections’ on the interface, correspondingly. By vibro-excitation tests, all the FRF-matrices of Eq. (3) are obtained respectively in these five cases of experimental models with “point-coupling connection” in free state. The point-distributions of vibro-excitation and displacement response are shown in Fig. 4, correspondingly, and the testing frequencies are set in 0-300 Hz.
Fig. 3Experimental model of mechanical assembly with linear connection

a) Before connection

b) After connection
Fig. 4Testing point-distributions in five cases of ‘point-to-point connections’ of the experimental model

a) Mono-coupling connection

b) Bi-coupling connection

c) Tri-coupling connection

d) Quad-coupling connection

e) Pent-coupling connection
4. Experimental results
After testing all the entries of the 6 FRF-matrices involved in Eq. (3) in the above five cases of “point-to-point connections” on the experimental model of mechanical assembly with linear connection, the matrix of the coupling dynamic stiffness of the assembly is computed by Eq. (3) for the cases, respectively. The mean module spectra, , of diagonal entries of the matrix, ( is the ordinal number of coupling points), in the five cases are plotted in Fig. 5, which is amplified in range of 130-170 Hz, as shown in Fig. 6.
To show the differences of the identified stiffnesses, here takes the average of the mean ( 1, 2, …, 5) in the five cases as a reference, denoted by . The relative errors, , of the five cases in full testing frequency range (0-300 Hz) are computed by:
where 400 is the number of discrete frequencies. The computed is listed in Table 1.
Fig. 5Mean |Ks(f)| in five cases of discrete connection
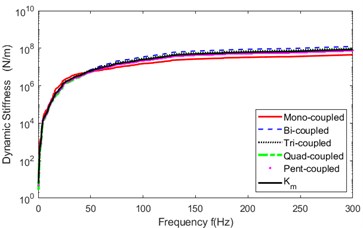
Fig. 6Amplified |Ks(f)| in 130-170 Hz for the five cases
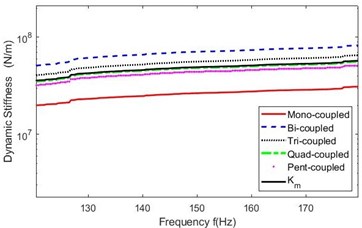
Table 1Relative errors Em of mean Ksf in the five cases with reference Kmf
Relative error of the second indirect scheme | Case of point-to-point connections | ||||
Mono-coupled | Bi-coupled | Tri-coupled | Quad-coupled | Pent-coupled | |
(%) | 47.8 | 46.3 | 15.0 | 2. 2 | 11.3 |
It can be seen that:
(1) The identified stiffnesses in the five cases are on the same order of magnitude, which is about 107 N/m and on the order of the steel stiffness, as shown in Fig. 5. This verifies that discretizing the linear connection of the coupling interface into “point-to-point connections” equivalently and applying the second indirect scheme to identify the stiffness of mechanical assembly is feasible in practice.
(2) Fig. 6 shows that the identified stiffness draws close to be stable with increase of the number of discretized points, close up to their average stiffness of the five cases.
(3) Table 1 shows that, for the experimental model in this study, discretizing its linear connection into four equivalent “point-to-point connections” results in the minimum relative error ( 2.2 %) to the average of the five cases. This illustrates implicitly that there exists probably an optimum number of discrete points for a specific mechanical assembly.
5. Conclusions
In order to apply the second indirect scheme of inverse substructuring analysis to identify the coupling dynamic stiffness of mechanical assembly with non-ideal connection, an experimental model with linear connection in-between the two components involved in the assembly is designed. Its connection is equivalently discretized into “point-to-point connections” in five cases at first. Then, the stiffness is computed by the scheme using the FRF-matrices tested by vibro-excitation. As the results of the experimental study, the scheme is firstly verified to be feasible in engineering application to the assembly with linear connection. With increase of the number of discretized points, the identified stiffness approaches to a stable value, e.g., the average of the five cases in this study. For the designed experimental model, four discrete points result in minimum relative error to the average. This means implicitly that an optimum number of discretizing the non-ideal connection of a mechanical assembly exists probably and is to be investigated further in detail next.
References
-
Implementation Manual of the Procedures and Specifications of Modern Machining and the National Assessment Standards of Mechanical Assembly Quality Inspection. China Machinery Industry Press, Beijing, 2011, (in Chinese).
-
Wang Bo, Tang Xiaoqing Decision-making of quality control for mechanical assembly activities. China Mechanical Engineering, Vol. 21, Issues 2, 2010, p. 164-168, (in Chinese).
-
Majid M., Graham E., Park S. S. FRF based joint dynamics modeling and identification. Mechanical Systems and Signal Processing, Vol. 39, Issues 1-2, 2013, p. 265-279.
-
Damjan C., Miha B. Identification of the dynamic properties of joints using frequency response functions. Journal of Sound and Vibration, Vol. 317, Issues 1-2, 2008, p. 158-174.
-
Hwang H. Y. Identification techniques of structure connection parameter using frequency response functions. Journal of Sound and Vibration, Vol. 212, Issue 3, 1998, p. 469-479.
-
Teik Lim C., et al. An improved numerical procedure for the coupling of dynamic components using frequency response functions. Proceedings of the 9th International Modal Analysis Conference, Florence, Italy, 1991, p. 902-908.
-
Zhen J. T., Lim T. C., Lu G. Q. Determination of system vibratory response characteristics applying a spectral-based sub-structuring approach, part I: analytical formulation. International Journal of Vehicle Noise and Vibration, Vol. 1, Issues 1-2, 2004, p. 1-30.
-
Lu Guang Qing, Wang Zhi Wei, Wang Lei Inverse sub-structuring analysis and computations of dynamic characteristics of transportation packaging system. Packaging Engineering, Vol. 27, Issue 4, 2006, p. 12-14, (in Chinese).
-
Lu Guang Qing Inverse sub-structuring analysis of dynamic stiffness of discretized coupling unit-of-packaging. Noise and Vibration Control, Vol. 29, Issue 2, 2009, p. 16-18, (in Chinese).
-
Lu Guangqing Yi Chuijie, Fang Ke Analysis and inverse substructuring computation on dynamic quality of mechanical assembly. Chinese Journal of Mechanical Engineering, Vol. 29, Issue 3, 2016, p. 539-548.
-
Lu Guangqing, Fang Ke, Pang Dongmei Substructuring analysis and quantitative computation on dynamic quality of mechanical assembly. Mechanical Science and Technology for Aerospace Engineering, Vol. 35, Issue 6, 2016, p. 840-845, (in Chinese).
-
Guang Qing Lu, Ke Fang, Dong Mei Pang Eigenvalue analysis and estimation on dynamic quality of mechanical assembly. Journal of Vibroengineering, Vol. 17, Issue 8, 2015, p. 4390-4403.
-
Lu Guangqing Yi Chuijie, Fang Ke Inverse substructuring methods for identifying coupling dynamic stiffness of mechanical assembly. Journal of Mechanical Engineering, Vol. 52, Issue 9, 2016, p. 86-95, (in Chinese).
About this article
The authors acknowledge gratefully National Natural Science Foundation of China for supporting research Project (Grant No. 51475211), and Provincial-ministerial University-industry Cooperation Project (Grant No. 2013B090600142) of Guangdong Provincial Department of Science and Technology, including the study of this paper.
