Abstract
In this paper, considering the moment of inertia and shear deformation, the partial differential equation sets governing the vibration of viscoelastic Timoshenko beam subjected to random excitations were derived. The excitation form is the concentrated force, and its random characteristic is the ideal white noise in the time domain. Two damping mechanisms, namely, the external viscous damping and the internal viscoelastic damping (Kelvin-Voigt model), are both taken into account simultaneously. Comparing with the existing literature, there are two improvements: on the one hand, considering the interaction of the rotational inertia and shear deformation, that is, there is a fourth derivative term for time in the partial differential equation sets of Timoshenko beam, while the Bresse-Timoshenko truncated model ignores the fourth derivative term of time. On the other hand, by the method of residue integral, the infinite integral in the mean response is transformed into the expression of the modal damping ratio and the natural frequency. The exact solution of the mean square response is obtained in the form of an infinite series finally. Numerical example is supplied, and the numerical results acquired verify the validity of the theoretical analysis.
1. Introduction
Prior to the 1980s, only two scholars, Houdijk and Eringen [1, 2], had derived the closed-solution of the probabilistic characteristics of the response of finite-length beam. The former provided the closed-form solutions of the mean square displacement of the tip of a uniform cantilever Bernoulli-Euler beam under space- and time-wise ideal white noise. In this paper, only the transverse damping was taken into account. The latter deduced the closed expressions for the space-time correlation functions of the supported beam.
After the 1980s, Elishakoff studied in detail the closed solution of the stochastic statistical properties of the finite length beams. In 1984, they studied the statistical characteristics of random vibrations of the Euler-Bernoulli simply supported beam under the different damping mechanisms, and founded that the displacement mean square response converges under the various damping mechanisms, while the stress mean square value does not converge when the rotational damping is considered [3]. In 1989, the former two experts used the truncated Bresse-Timoshenko simply supported beam as the research object, and derived the expressions of the mean square response of displacement and velocity [4]. In 2018, Hache and Elishakoff et al. studied further the critical comparisons of the exact solutions in random vibration of the supported beams using three versions of the Bresse-Timoshenko theory [5].
In this paper, the interactions of the moment of inertia and the shear deformation are considered, and the fourth derivative term of time in the governing equation of the Timoshenko beam is not ignored. Two types of damping mechanism, i.e. the external viscous damping and the internal viscoelastic damping, are both taken into account simultaneously. Both damping mechanisms are taken into account simultaneously, and this approach is more in line with objective reality. By using the residue integral method, the infinite integral in the mean square response is transformed into the expression of the modal damping ratio and the natural frequency, and then the mean square response is expressed in the form of infinite series finally. The accuracy of the theoretical analysis is verified by providing a numerical example.
2. Damping vibration theory
2.1. Governing equations
In this paper, the Kelvin-Voigt model is used to described the constitutive relation of material, and its expression is listed as follows:
where , , , , , , , are the normal stress, the shear stress of the material, the normal strain, the shear strain, the Young’s elastic modulus, the shear elastic modulus, the Poisson ratio and the Voigt damping coefficient respectively. is the first derivative with respect to time, namely, the comma of the subscript indicates the partial derivative, and the letter followed by the comma denotes the partial derivative of the physical quantity represented by the letter. In this paper, the partial derivatives are all written in this form.
A uniform cantilever beam of length is shown in Fig. 1. The beam is subjected to a lateral concentrated force at a distance .
Fig. 1A cantilever beam subjected to a concentrated force
, are the bending moment and the shear force at the microelement cross section severally. Based on the elementary deflection theory and the constitutive relation of materials Eq. (1), the expressions of the bending moment and the shear force can be obtained as:
where , denote the transverse displacement and the slope of the deflection curve respectively, – the section area, – the shear coefficient, – the moment of inertia of cross-section.
In terms of the D’alembert principle, the differential equations of the viscoelastic Timoshenko beam subjected to a concentrated force can be deduced, as follows:
2.2. Free vibration analysis
When , the expressions of the displacement model function and the rotation model function can be written as [6]:
where, , , , , , , , – the natural frequency, the integral constant and can be determined by boundary conditions.
0 are the boundary conditions of the cantilever beam, and substituting the expressions into Eqs. (5) and (6), the frequency equation of the cantilever beam is obtained as follows:
where , .
From the literature [7], the orthogonal relations of the modal modes are gained:
where, and are the th main mass and stiffness, the symbol denotes the Dirac function and is consistent with the notation in Eq. (4).
2.3. Forced vibration analysis
The displacement function and the deflection function are expanded to the infinite series according to the regular mode, , . is the steady regular modal response. In the light of the orthogonal conditions in Eq. (8), the differential equations in Eq. (4) can be decoupled as follows:
where denotes the regular mode excitation, is the modal damping ratio. Their expressions can be deduced as:
On the basis of the Duhamel integral [8], the transverse displacement solution in Eq. (4) can be derived as follows:
where denotes the th unit impulse response function and its expression is:
Depending on Eq. (11), the value of the modal damping ratio increases with the growth of the modal order and the internal viscoelastic damping makes it happen. Because of the role of the internal damping, the higher order modal responses will attenuate faster, which lead to the infinite series in Eq. (12) converge faster.
3. Random vibration theory
In this paper, the applied load is the concentrated force, which is the ideal white noise in the time domain. For the sake of simplicity and universality, it is assumed that the mathematical expectation of the stochastic concentrated force excitation is zero, so does the random response for the linear system.
3.1. Statistical characteristics of the concentrated force
It is assumed that the autocorrelation function and the power spectral density function of the concentrated force excitation are and , respectively.
Make use of the stochastic process theory, combing with Eq. (10), it is easy to obtain the cross-correlation function of the arbitrary regular mode excitation and :
where the symbol represents the mathematical expectation. denotes the time interval.
Applying the Fourier transform to Eq. (14), the cross-power spectral density function can be deduced as:
3.2. Statistical characteristics of the transverse displacement response
In the light of the mean square calculus, combing with Eq. (12) and Eq. (14), the autocorrelation function of the transverse displacement response can be acquired as:
Applying the Fourier transform to Eq. (16), combing with Eq. (15), the power spectral function of the transverse displacement response can be derived as follows:
where denotes the th amplitude frequency response function and its expression is:
On the basis of the stochastic process theory, if the mean square value exists, make use of Eq. (17), the mean square displacement, velocity and acceleration responses can be deduced as follows:
where:
The bandwidth of the ideal white noise power spectral density function is spread all over the horizontal axis, and the infinite integral is converted into the expression of the natural frequency and the modal damping ratio by utilizing the residue integral theorem [9]. Their results are:
where .
4. Numerical example
The material of the homogeneous cantilever beam is steel. The physical parameters are shown in Table 1, and the geometric parameters are shown in Table 2.
Table 1Physical parameters
(GPa) | (GPa) | (kg/m3) | (N·s/m) | (N·s/rad) | (Pa·s) |
206 | 80 | 7900 | 0.1 | 0.1 | 7×104 |
Table 2Geometric parameters
(m) | (m2) | (m4) |
1 | 0.02 | 6.67×10-5 |
where the section height = 0.2 m and the width = 0.1 m | ||
Table 3Vibration parameters
Vibration parameters | First order | Second order | Third order | Fourth order | Fifth order |
(Hz) | 160.02 | 862.63 | 2054.61 | 3412.96 | 4855.17 |
0.002 | 0.013 | 0.032 | 0.053 | 0.076 | |
0.077 | 0.065 | 0.050 | 0.035 | 0.022 |
In terms of the theory of chapters 2 and 3, the natural frequency, the modal damping ratio and the integral constants can be obtained by calculation, and their results are shown in Table 3. However, it only shows the values of vibration parameters of the first five orders.
According to Eq. (20) and (21), combing with 5, the values of and constitute severally a 5×5 real symmetric matrix, and the numerical results are as follows:
The numerical results show that, when 1, the value in each matrix accounts for about 95 % of the total value, indicating that the first-order mode has the greatest impact on the whole system. According to the values in each matrix, we can further reduce the index value of the infinite series in the mean square response, and take 3 not 5. Hence, the values of and can be used as a basis for the truncation of the mode in random vibration.
Assuming that a concentrated force is located at 0.6, the power spectral density function of the acceleration response can be derived as in terms of Eq. (16). Let 1 m2s, the graph of the power spectral density function of the acceleration response is shown in Fig. 3. There are three peaks in Fig. 3, respectively at the first three natural frequencies. The energy of the first mode is the largest, and far greater than the rest, which corresponding to the values of the matrix and . As the modal order increases, the energy gradually decreases.
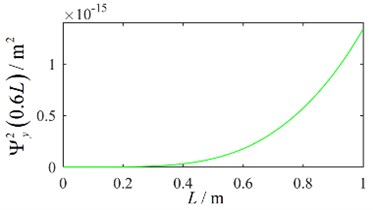
The displacement square response under the concentrated force excitation of ideal white noise is drawn in Fig. 4. The mean square value of the displacement response varies monotonously along the length of the cantilever beam, and reaches the maximum at the free end.
Fig. 3Acceleration response spectrum
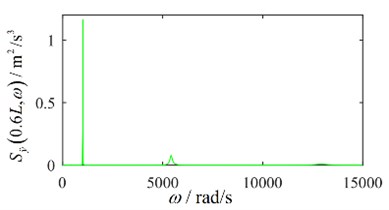
Fig. 4Displacement square response
5. Conclusions
In this paper, the random vibration characteristics of Timoshenko cantilever beam are studied. Considering the joint influence of the external viscous damping and the internal viscoelastic damping, two types of damping mechanism are introduced into the partial differential equations concurrently to make the damping mechanism more in line with the actual situation.
Compared with the existing literature, in the process of calculating the mean-square response, the method of residue integral is used to transform the infinite integral in the mean square response into the expression of the modal damping ratio and the natural frequency, so as to obtain the exact solution of the infinite series form of the mean square response. In addition, the numerical results of and can be used as a basis for mode truncation.
The numerical results show that with the growth of modal order, the modal damping ratio gradually increases, that is, the viscoelastic damping inhibits the response of higher order mode. The power spectrum of the acceleration response has obvious peak value at the natural frequency, and the maximum value of the displacement mean square response occurs at the free end.
References
-
Houdijk A. Le mouvement brownien d’un fill. Archives Neerlandaises des Science Exactes et Naturelles, Vol. 3, 1928, p. 212-277.
-
Eringen A. C. Response of beams and plates to random loads. Journal of Applied Mechanics, Vol. 24, 1957, p. 46-52.
-
Elishakoff I., Livshits D. Some closed-form solutions in random vibration of Euler-Bernoulli beams. Journal of Probabilistic Engineering Mechanics, Vol. 4, Issues 11-12, 1986, p. 1291-1301.
-
Elishakoff I., Livshits D. Some closed-form solutions in random vibration of Bresse-Timoshenko beams. Journal of Probabilistic Engineering Mechanics, Vol. 4, Issue 1, 1989, p. 49-54.
-
Hache F., Elishakoff I., Challamel N. Critical comparison of exact solutions in random vibration of beams using three versions of Bresse-Timoshenko theory. Journal of Probabilistic Engineering Mechanics, Vol. 53, 2018, p. 95-108.
-
Huang T. C. The effect of rotatory inertia and of shear deformation on the frequency and normal model equation of uniform beams with simple end conditions. Journal of Applied Mechanics, Vol. 28, Issue 4, 1961, p. 579-584.
-
Huang T. C. Effect of rotatory inertia and shear on the vibration of beams treated by the approximate methods of Ritz and Galerkin. Proceedings of The Third U.S. National Congress of Applied Mechanics, 1958, p. 189-194.
-
Thomson W. T., Dahleh M. D. Theory of Vibration with Applications. 5th edition, Pearson Prentice Hall, New Jersey, 1998.
-
Lang S. Complex Analysis. 4th Edition, Springer-Verlag, New York, 1999.
