Abstract
Identifying coupling dynamic stiffness of structural connection is often needed in substructural dynamic analysis. To overcome the faultiness of conventional approaches existed, five indirect schemes of inverse substructuring analysis by using tested frequency response functions (FRFs) are provided. And the first indirect scheme is verified by three mass-rubber models constructed as two-level substructures with mono-coupling, bi-coupling and tri-coupling connection. Compared to existing direct scheme of inverse substructuring analysis, it shows better performance with acceptable precision of determining the stiffness.
1. Introduction
Dynamic substructuring analysis based on frequency response function (FRF) has been paid attentions widely in mechanical structural dynamics. There were a number of researches reported in parameter identification of coupling dynamic characteristics of connected structures [1-6]. For instances, to overcome the faultiness of modal analysis that needs to establish mass-damping-stiffness matrices for modeling, HWANG [3] applied FRF-model to identify parameters of the connection between structures, and eliminate low-precision of the identification at high-sensitive frequency range by use of statistical averages; Targeting at the difficulty of precisely modeling structural connecting dynamic properties by pure analytical approaches, DAMJAN and MIHA [5] identified the dynamic flexibility of bolted connection of beam structures and proposed modeling method in consideration of both translational degrees of freedom (TDOF) and rotational degrees of freedom (RDOF); MAJID et al. [6] used inverse receptance coupling(IRC) and point-mass-connecting model, which considers the connection as an element of mass-damping-stiffness, to identify connecting characteristics, and combined FEM-simulation with FRF-tests to prove the results. These research works obtained the connecting parameters with errors to different extent for sorts of structural connections. However, they are essentially of “positive” substructuring analysis at all, which needs to pre-determine the connecting boundary conditions and or some of structural dynamic metrics. Therefore, the computations and or their algorithms are complicated, testing and computational expenses in application are heavy, resulting in partial identified outcomes affected by modal coupling need to be modified via FEM and or statistical schemes.
Inverse substructuring dynamic analysis based on FRF-spectra can be used to determine both substructural and coupling dynamic characteristics of structural system with different sorts of connection. It is simple with less computations, and has no needs of complicated modal tests, synthesis, pre-determined constraint boundary conditions, such as structural coupling parameters [7]. LU introduced the direct scheme of inverse substructuring dynamic analysis firstly to fix the dynamic stiffness of coupling-unit-of-packaging [8]. And he also applied FRF-based inverse substructuring approach to analyze the dynamic characteristics [9] and do eigenvalue analysis on mechanical assembly [10]. Afterwards both direct scheme and indirect schemes of inverse substructuring analysis were introduced to analyze the dynamic quality of a mechanical assembly [11], including identification on its coupling dynamic stiffness [12], but lack of verification experimentally on them.
This study provides five potential indirect schemes of inverse substructuring analysis to determine the coupling dynamic stiffness of structural connection. Compared to existing direct scheme of inverse substructuring analysis, the first indirect scheme is verified experimentally by tested FRFs on three mass-rubber models of two-level substructures with mono-coupling, bi-coupling and tri-coupling connection. As result of this study, the first indirect scheme shows better performance with acceptable precision of determining the stiffness of structural connection.
2. Determining coupling dynamic stiffness of structural connection by inverse schemes
Fig. 1 shows a dynamic structural system with two-level substructures A and B connected via connector. Fig. 1(a) and Fig. 1(b) indicate the dynamic excitation-force (), displacement response (), and representative transfer-function () before and after connection of A and B, named as “FRF at component level” (without subscript ) and “FRF at system level” (with extra subscript ), respectively. The connection is characterized by “coupling dynamic stiffness ()”. Lowercase , and indicate substructures A, B and their coupling connector, and and represents excitation-force input and displacement-response output, respectively. Thus, for examples, FRFs and represents transfer-functions from excitation force on coupling interface on substructure A () to output displacement-response on A () without connecting with B, and from excitation input excitation-force on B to output displacement-response on A connecting with B, respectively.
Fig. 1FRFs of two-level substructures at component level a) and system level b)
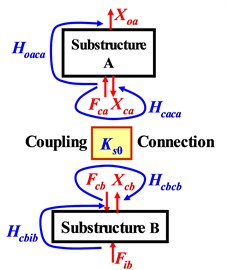
a) Before connection
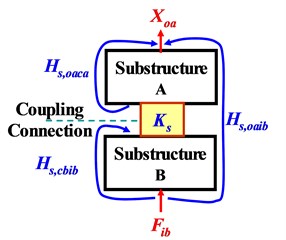
b) After connection
The dynamic stiffness matrix, [], of structural connection can be inversely determined by [7, 12]:
where, denotes inverse and transpose operation of matrix. Eq. (1) is often classified as “direct scheme of inverse substructuring dynamic analysis”. Determining [] needs the tested FRFs, , and on both sides of the coupling interfaces of substructures A and B in connection with each. Sometimes, it is hard to do the tests in practice, even impossible in case of very close-connection.
To overcome the difficulty of the direct scheme for FRF-tests in engineering applications, Five indirect schemes of inverse substructuring analysis are formulated here. The FRFs at system level can be related to the FRFs at component level by [7]:
where, , +1, −1 for and , and +1, −1 for and , respectively.
Considering all independent equalities in Eq. (2), and substructure A can be mutually exchanged in practice, if choose the number of input excitation-force (, ) to be the same as those of both displacement-response ouputs (, ) and the connection points at coupling interfaces (, ), then, five indirect schemes of inverse substructuring analysis to determine coupling dynamic stiffness matrix [] of a structural connection can be formulated as follow:
where:
and [] is unity matrix with same size of the FRF-matrices. For mono-coupling connection, there is only one entry in the matrices of Eqs. (4)-(8), i.e., they can be expressed in algebraic form as follow:
where:
Eqs. (4)-(8) and or Eqs. (9)-(13) are named here as the first to fifth indirect schemes of inverse substructuring analysis for determining coupling dynamic stiffness of structural connection, due to use of FRFs at both system level and component level in computation. FRFs involved in Eqs. (4)-(13) are needed to be tested before computing the stiffness.
3. Experimentally verification on the first indirect scheme
To verify the effectiveness of the indirect schemes of inverse substructuring analysis in determining coupling dynamic stiffness of a structural connection, three experimental models of two-level substructures are established and constructed as shown in Fig. 2. Where, single, two and three point(s) of structural connection are named as “mono-, bi- and tri-coupling”, respectively, in this study. Their lumped-parameters are measured and listed in Table 1.
Using analytical lumped-parameter study, all of the five indirect schemes are analytically validated at first by applying them to the tri-coupling connection, as shown in Fig. 2(c). The moduli of coupling dynamic stiffness are computed by Eqs. (4)-(8) using the lumped-parameters in Table 1. The results are shown in Fig. 3, compared to that by direct scheme Eq. (1) and the measured ones (calculated by , pure imaginary unit, and , analytical frequency in Hertz). From Fig. 3, it can be seen that, the dynamic stiffness computed by both direct and indirect schemes are exactly identical, and they are also right the same as the measured ones. Therefore, the five indirect schemes are analytically valid in determining coupling dynamic stiffness of structural connection, as it does by direct scheme.
Fig. 2Experimental models of two-level substructures
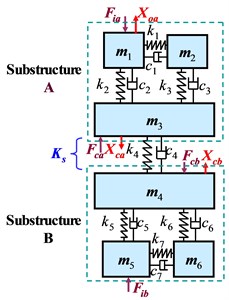
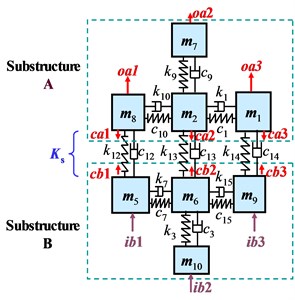

a) Mono-coupled connection

b) Bi-coupled connection

c) Tri-coupled connection
To experimentally verify the indirect schemes, here target only the first one as an example. Using the tested FRFs involved in the direct scheme Eq. (1) and the 1st indirect scheme Eqs. (4) and (9) on the three models in Fig. 2, the coupling dynamic stiffness are computed by the equations respectively, and shown in Fig. 4, compared with the measured ones. The computed stiffness are also fitted by LS curve fittings. Table 2 lists the fitted stiffness, compared with the measured ones, including their relative errors.
It can be seen that, (i) both direct and indirect schemes can be applied to determine the coupling dynamic stiffness of structural connection with acceptable precision for the three models, especially the mean relative error for static stiffness can be lower than 10 %; (ii) The 1st indirect scheme shows better performance with mean relative errors of 1.9 % and 46 % in determining static stiffness and damping factor , compared to that of direct scheme with the errors of 8.1 % and 68.1 % respectively; (iii) The relative errors of determining damping factors are much greater than that of determining static stiffness. They are probably resulted from LS curve fitting, damping ratio tests and or nonlinear effects of both static stiffness and damping factor.
Table 1Measured lumped-parameters of the three experimental models
Mass (kg) | Static stiffness (kN/m) | Samping factor (kNs/m) | Mass (kg) | Static stiffness (kN/m) | Samping factor (kNs/m) | ||||||
1.86 | 799 | 0.365 | 1.17 | 680 | 0.286 | ||||||
1.64 | 646 | 0.346 | 1.62 | 663 | 0.356 | ||||||
1.75 | 655 | 0.242 | 189 | 0.163 | |||||||
1.76 | 198 | 0.135 | 188 | 0.146 | |||||||
1.41 | 682 | 0.495 | 206 | 0.201 | |||||||
1.28 | 698 | 0.465 | 202 | 0.188 | |||||||
1.18 | 691 | 0.437 | 698 | 0.302 | |||||||
1.25 | 671 | 0.369 | |||||||||
Fig. 3Measured and computed [Ks] using analytical FRFs of tri-coupled model Fig. 2(c) by direct scheme, Eq. (1), and five indirect schemes, Eqs. (4)-(8)
![Measured and computed [Ks] using analytical FRFs of tri-coupled model Fig. 2(c) by direct scheme, Eq. (1), and five indirect schemes, Eqs. (4)-(8)](https://static-01.extrica.com/articles/18016/18016-img9.jpg)
Table 2Measured and fitted Ks=ki kN/m+jωci(kNs/m) and their relative errors (%)
Connection | Mono-coupled | Bi-coupled | Tri-coupled | |||||||||
Measured | 198 | 0.135 | 198 | 0.135 | 189 | 0.163 | 188 | 0.146 | 206 | 0.201 | 202 | 0.188 |
Fitted by Direct scheme | 188.4 | 0.246 | 197.2 | 0.300 | 140.7 | 0.249 | 177.5 | 0.239 | 187.1 | 0.264 | 196.5 | 0.294 |
Relative error | 4.8 | 82.2 | 0.4 | 122.2 | 25.6 | 52.8 | 5.6 | 63.7 | 9.2 | 31.3 | 2.7 | 56.4 |
Fitted by 2nd Indirect scheme | 197.5 | 0.229 | 192.5 | 0.201 | 179.4 | 0.191 | 185.8 | 0.233 | 201.8 | 0.247 | 196.5 | 0.296 |
Relative error | 0.3 | 69.6 | 0.25 | 48.9 | 5.1 | 17.2 | 1.2 | 59.6 | 2.0 | 22.9 | 2.7 | 57.5 |
Mean relative error | Scheme | Direct | 1st Indirect | |||||||||
8.1 | 1.9 | |||||||||||
68.1 | 46.0 | |||||||||||
Fig. 4Measured and computed [Ks] using tested FRFs on mono-, bi- and tri-coupling models in Fig. 2 by direct and the 1st indirect scheme
![Measured and computed [Ks] using tested FRFs on mono-, bi- and tri-coupling models in Fig. 2 by direct and the 1st indirect scheme](https://static-01.extrica.com/articles/18016/18016-img10.jpg)
a) Mono- coupling
![Measured and computed [Ks] using tested FRFs on mono-, bi- and tri-coupling models in Fig. 2 by direct and the 1st indirect scheme](https://static-01.extrica.com/articles/18016/18016-img11.jpg)
b) Bi- coupling
![Measured and computed [Ks] using tested FRFs on mono-, bi- and tri-coupling models in Fig. 2 by direct and the 1st indirect scheme](https://static-01.extrica.com/articles/18016/18016-img12.jpg)
c) Tri-coupling
4. Conclusions
To determine coupling dynamic stiffness of substructural connection, this study provides five indirect schemes of inverse substructuring analysis. Compared to existing direct scheme, they are well validated analytically, and as example, the first indirect scheme is further verified experimentally. Results from the study are concluded as follow:
1) The five indirect schemes are analytically valid in determining coupling dynamic stiffness, for which they are right identical to the direct scheme.
2) The first indirect scheme has better precision in determining coupling dynamic stiffness than the direct scheme. The relative errors for static stiffness and damping factor of the models are 1.9 % and 46 % respectively, much less than that of direct scheme. The verifications on the rest four indirect schemes are to be completed by next work.
3) The relative error for determining damping factor is much greater than that for static stiffness. This may be resulted from LS curve fitting, damping test, and or nonlinear effect of the stiffness, and is to be investigated and improved in further study.
References
-
Yang K. T., Park Y. S. Join structural parameter identification using a subset of frequency response function measurement. Mechanical Systems and Signal Processing, Vol. 7, 1993, p. 509-530.
-
Ren Y., Beards C. F. Identification of joint properties of a structure using FRF data. Journal of Sound and Vibration, Vol. 186, 1995, p. 567-587.
-
Hwang H. Y. Identification techniques of structure connection parameters using frequency response functions. Journal of Sound and Vibration, Vol. 212, Issue 3, 1998, p. 469-479.
-
Yang T., Fan H. S., Lin S. C. Joint stiffness identification using FRF measurements. Computers and Structures, Vol. 81, 2003, p. 2549-2556.
-
Damjan C., Miha B. Identification of the dynamic properties of joints using frequency-response functions. Journal of Sound and Vibration, Vol. 317, Issue 3, 2008, p. 158-174.
-
Majid M., Eldon G., Park S. S. FRF based joint dynamics modeling and identification. Mechanical Systems and Signal Processing, Vol. 39, 2013, p. 265-279.
-
Zhen J. T., Lim T. C., Lu G. Q. Determination of system vibratory response characteristics applying a spectral-based inverse sub-structuring approach. Part 1: Analytical formulation. International Journal of Vehicle Noise and Vibration, Vol. 1, Issues 1-2, 2004, p. 1-30.
-
Lu Guangqing Inverse substructuring analysis of dynamic stiffness of discretized coupling unit-of- packaging. Noise and Vibration Control, Vol. 29, Issue 2, 2009, p. 16-18, (in Chinese).
-
Lu Guang-qing, Wang Jun, Pang Dong-mei Investigation on dynamic characteristics of mechanical assembly. Vibroengineering Procedia, Vol. 5, 2015, p. 53-58.
-
Lu Guang-qing, Fang Ke, Pang Dong-mei Eigenvalue analysis and estimation on dynamic quality of mechanical assembly. Journal of Vibroengineering, Vol. 17, Issue 8, 2015, p. 4390-4403.
-
Lu Guangqing, Yi Chuijie, Fang Ke Analysis and inverse substructuring computation on dynamic quality of mechanical assembly. Chinese Journal of Mechanical Engineering, Vol. 29, Issue 3, 2016, p. 539-548.
-
Lu Guangqing, Yi Chuijie, Fang Ke Inverse substructuring methods for identifying coupling dynamic stiffness of mechanical assembly. Journal of Mechanical Engineering, Vol. 52, Issue 9, 2016, p. 86-95, (in Chinese).
About this article
The authors acknowledge gratefully National Natural Science Foundation of China for supporting research Project (#51475211), and Graduates Innovation Training Projects of Guangdong (#1055915007) and Jinan University (#CX15040), including the study of this paper.
