Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates

Ike, Charles Chinwuba; Mama, Benjamin Okwudili

doi:10.21595/mme.2018.19750

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 31 March 2018

Check for updates

Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates

Charles Chinwuba Ike¹

Benjamin Okwudili Mama²

¹Department of Civil Engineering, Enugu State University of Science and Technology, Enugu, Enugu State, Nigeria

²Department of Civil Engineering, University of Nigeria, Nsukka, Nigeria

Corresponding Author:

Charles Chinwuba Ike

Cite the article Download PDF

Downloads 1678

CrossRef Citations 5

Abstract

The Kantorovich variational method was used in this study to solve the flexural problem of Kirchhoff-Love plates with two opposite edges $x = \pm a / 2$ clamped and the other two edges $y = \pm b / 2$ simply supported, for the case of uniformly distributed transverse load over the entire plate domain. The plate considered was assumed homogeneous, and isotropic. The total potential energy functional for the Kirchhoff-Love plate was found as the sum of the potential energy of the applied distributed load and the strain energy functional of the plate. The symmetrical nature of the plate and the load was used to choose the deflection function as a single series of infinite terms involving the cosine function of the y coordinate variable with the unknown function being dependent on the $x$ coordinate variable. Integration with respect to the $y$ coordinate variable simplified the total potential energy functional to be dependent on the unknown function of $x$ , and its derivatives. Euler-Lagrange differential equations were used to find the differential equations of equilibrium of the plate as a system of homogeneous fourth order ordinary differential equations (ODE) in the unknown function. The system of fourth order ODE was solved using the method of differential D operators, or the method of trial functions to obtain the general solution as the linear superposition of the homogeneous and particular solutions. The demands of symmetry of unknown function about the point $x =$ 0, and the boundary conditions at the clamped edges were used to obtain all the four integration constants; thus, completely determining the deflection. Bending moment distributions were determined using the bending moment deflection relations. The deflection was determined at the centre of the plate. The bending moment values were also determined at the centre of the plate, and at the middle of the clamped edges. Expressions obtained for the deflection at the centre, and bending moment values were found to be single series of infinite terms with highly converging properties. The solutions obtained converged to the exact solutions with the use of only four terms of the series.

1. Introduction

Plates are three dimensional structures that have one (transverse) dimension that is very small relative to the other two (in-plane) dimensions [1, 2]. They are commonly used in structural applications in buildings, machine parts, ships, aircrafts, aerospace structures and naval facilities. They are commonly subjected to transversely applied distributed and/or point forces and thus carry such forces by the development of bending moments in the two in-plane directions and a twisting moment. They can be required to carry in-plane forces applied in in-plane directions.

The analysis of plates employs the three-dimensional theory of elasticity [1]. They are governed by the simultaneous requirements of the generalized Hooke’s law of linear elasticity, the strain – displacement relations, and differential equations of equilibrium, subject to the boundary conditions imposed by the restraints and the load [3-6]. The exact three-dimensional elasticity theory has often been simplified using approximations offered by the smallness of the transverse coordinate dimension, thus reducing the problem to two dimensional approximations [7, 8].

In general, three broad theories exist for modelling plates. They are:

(i) Thin plate theories (8...10 $\leq a / h \leq$ 8...100), where $a$ is the least in-plane dimension, and $h$ is the plate thickness:

– small deformation thin plate theories (Kirchhoff-Love plate theory);

– large deformation thin plate theories (von Karman Plate theory).

(ii) Moderately thick plate theories (Reissner [9] plate theory, Mindlin [10] plate theory) and,

(iii) Thick plate theories ( $a / h \leq$ 8...10).

2. Review of plate theories

There are several types of plate theories. The basic idea of all plate theories is to simplify the three-dimensional (3D) plate problem defined by the mathematical theory of elasticity to two dimensional approximations. This is usually achieved by integrating out one of the dimensions. Usually, the plate’s transverse dimension is integrated out by expressing stresses using stress resultants.

Thick plates can only be solved using the mathematical theory of elasticity, involving a simultaneous solution of a system of fifteen equations – namely the stress – strain laws, the strain displacement relations and the differential equations of equilibrium. The solutions of thick plate problems are mathematically rigorous, and only few thick plate problems involving simple plate geometries, load and boundary conditions have so far been successfully solved.

Moderately thick plates are described using plate theories due to Reissner, [9] Mindlin, [10] Reddy; Shimpi [11] Levinson and Chandrashekhara [12]. Reissner [9] presented a stress formulation of the problem of moderately thick plates using the Castigliano’s energy minimization principle by assuming that the in-plane stresses are linear, the transverse shear stresses are quadratic and the transverse normal stresses are cubic in the plate transverse direction. Using the stress – equilibrium equations of the 3D theory of elasticity, and the stress – strain laws, Reissner applied the Castigliano’s principle and obtained the governing equations of Reissner plates as an integration problem of sixth order. The advantages of Reissner’s plate theory include:

(i) The theory incorporates first order shear deformation effects.

(ii) It is suitable for moderately thick plates where thickness is of the order of one tenth of the governing (least) planar dimension.

(iii) The linear distribution of bending stress and the quadratic distribution of shear stress used in the theory are consistent with the theory of elasticity.

The disadvantages (limitations) of Reissner’s plate theory are:

(i) The theory results in a sixth order boundary value problem (BVP) which is mathematically rigorous.

(ii) The plate problem is represented in terms of three unknown degrees of freedom involving generalized displacements.

(iii) The BVP is given as a system of three coupled partial differential equations for which solutions are mathematically demanding.

Mindlin [10] presented a first order shear deformation plate theory by extending the kinematics of the classical plate theory (CPT) by including transverse shear strains and removing the normality restriction. He further assumed that the displacement field can be described in terms of three generalized displacement parameters. Using the stress – strain laws, the strain displacement relations and the differential equations of equilibrium, Mindlin derived the governing differential equations of equilibrium as a system of three coupled differential equations in terms of the unknown generalized displacement parameters. The advantages of the Mindlin plate theory are:

(i) The theory includes shear deformation and rotary inertia effects.

(ii) The Kirchhoff-Love plate theory is recovered from the Mindlin plate theory by imposing the normality conditions. Thus, the Kirchhoff plate theory can be considered a special case of the Mindlin plate theory.

The limitations of the Mindlin plate theory include:

(i) The assumption of constant shear strain over the plate thickness violates the theory of elasticity results. Mindlin introduced shear correction factors to ensure the correct amount of internal energy is predicated by the Mindlin theory.

(ii) Shear free boundary conditions on the plate surfaces are violated.

(iii) The theory offers no mathematically logical way to determine the shear correction factor, $k$ .

This study adopts the classical Kirchhoff-Love plate theory. The theory used the Kirchhoff’s three hypotheses to simplify and approximate the three-dimensional elasticity problem to two dimensions. They are:

(a) Straight cross-sections perpendicular to the neutral surface of the plate before flexure remain straight and orthogonal after the deformation.

(b) The normal stress in the transverse direction is so insignificant and is neglected; thus, simplifying the three dimensional generalised Hooke’s stress – strain relations to two dimensions.

(c) The transverse shearing strains $γ_{x z}$ and $γ_{y z}$ are assumed to be zero. This implies that the plate thickness does not change under flexural deformation.

Several methods have been used to solve the Kirchhoff-Love plate bending problem. The methods are categorized into two, namely: classical methods and approximate (numerical) methods. The classical methods used include: the Navier’s double trigonometric series methods [13], the symplectic elasticity methods [14], the Levy’s single trigonometric series methods [13], the methods of eigen function expansions, the method of integral transformations [15]. The approximate (numerical) methods used include variational method [16-19] weighted residual method, Finite Difference method [20] finite element method, finite grid methods, Improved finite difference methods.

2.1. Review of methods of solving thin plate bending problems

Navier’s [21] double trigonometric series method was originally proposed to solve the Kirchhoff-Love plate bending problem with simply supported edges ( $x =$ 0, $a$ , $y =$ 0, $b$ ). The method assumes that (i) the load $p (x, y)$ is represented by a double Fourier sine series of infinite terms, where the Fourier coefficients of the load function are determined using the Fourier series theory (ii) the unknown deflection $w (x, y)$ is similarly expressed by a double Fourier sine series where the Fourier coefficients of the deflection are found from the governing partial differential equation of the Kirchhoff-Love plate problem [22]. The major limitation of the Navier’s method is the inability to be applied to plates with mixed boundary conditions.

Levy’s method was originally developed for rectangular Kirchhoff-Love plates with two opposite edges simply supported and the remaining two edges subject to arbitrary boundary conditions [23]. For the bending problem of rectangular thin plates $a \times b$ with simple supports at $x =$ 0, $a$ , and arbitrary support conditions at $y = \pm b / 2$ , Levy assumed that the unknown deflection can be assumed as a single Fourier sine series of infinite terms that automatically satisfies the simply supported boundary conditions at $x =$ 0, $a$ , where the unknown single Fourier series coefficients (a function of the y coordinate variable) are found by substitution of the single Fourier series representation for the deflection into the governing fourth order elliptic partial differential equation of the Kirchhoff-Love plate bending problem [22]. Levy further assumed the applied load is represented by a similar single Fourier series. Levy’s method reduced the fourth order PDF of the Kirchhoff-Love plate problem to a set of ordinary differential equations; which are solved to find the homogeneous and particular solutions. Enforcement of boundary conditions on the edges $y = \pm b / 2$ are used to find the constants of integration. The primary merit of Levy’s method is the advantage of a single Fourier sine series representation which is convenient and computationally effective.

Other advantages are:

(i) The boundary conditions along the edges $y = \pm b / 2$ are unspecified in the general solution and the integration constants can be determined for arbitrary support conditions at those edges.

(ii) Plates of finite width and semi-infinite extent can be solved by appropriate selection of integration constants.

(iii) The solutions are rapidly converging for distributed loads.

The disadvantages of the method are:

(i) It involves complicated mathematical analysis.

(ii) It encounters problems in dealing with point loads and problems involving discontinuities.

The numerical methods for solving the thin plate bending problems rely on finding approximate solutions to the problem. Thin plate bending problems have been alternatively formulated as variational problems, using the calculus of variations. Plate problems have been formulated using the minimum energy theorems which can be derived from the variation of strain energy of the elastic plate through variation in displacements or variations in the stresses.

The Ritz method for the analysis of thin plates in bending assume that the equilibrium equation of the plate is obtained by minimizing the total potential energy functional for the problem with respect to unknown displacement parameters. The Ritz method assume the deflection function is given in terms of a truncated linear combination of shape functions which satisfy the end conditions. The Ritz formulation reduces the problem of plate bending to an algebraic problem of finding the unknown displacement parameters of the deflection function. Aginam et al. [19] have used the Ritz variational method for thin plate bending problems.

Tian, Zhong and Li [24] used the double finite integral transform method to derive exact bending solutions of rectangular cantilever thin plates under arbitrary loading, which is one of the most difficult and intricate problems in the theory of elasticity due to its complexity in both the governing partial differential equations and the boundary conditions. The finite integral transformation analysis is performed rationally without any assumptions of trial functions for the unknown displacements, which demonstrates the advantage of the method of double finite integral transform over other methods. They showed the method presents an efficient and unified procedure for accurate plate bending analysis with potentials for extension to the solution of other boundary value problems such as buckling and vibration.

Johnarry [25] presented the method of acceleration displacement ratio transform of differentials for solving the bending problem of Kirchhoff-Love plates. He illustrated the use of the method with simply supported thin plates under uniformly distributed transverse loads over the plate domain and obtained solutions that were identical with the Navier’s solutions. He presented a similar illustration with the problem of simply supported thin plate under point load and obtained reasonably acceptable solutions.

The Galerkin method is a class of methods in numerical analysis for converting a continuous operator problem to a discrete problem [26]. In principle, it is the equivalent of applying the method of variation of parameters to a function space; thus, rendering the boundary value problem (BVP) to become a weak formulation. The method assumes an approximate solution to the unknown function in the BVP of thin plate bending to be expressed by a linear combination of $N$ base (basis or coordinate) functions that are linearly independent and satisfy the boundary conditions of the plate [27].

Galerkin weighted residual integral statement of the problem then converts the BVP to a system of linear algebraic equations in terms of the unknown displacement parameters of the trial function. The basis functions are the weighting functions in the Galerkin integral. The Galerkin method is more systematic and more general than many numerical methods and has been found to be computationally efficient. Osadebe et al. [16] have used the Galerkin method to solve thin plate problems.

This paper adopts the Kantorovich variational method because of the advantages of the method.

2.2. Advantages of the Kantorovich variational method

The Kantororvich variational method is used in this study because of the advantages over other analytical and numerical methods, namely:

(i) The method generally results in a rapidly converging solution and is an efficient computational method.

(ii) It has a close resemblance to the Rayleigh-Ritz and finite element methods due to the energy minimization principle which is at the heart of the method.

(iii) The method considerably reduces the amount of computational and numerical work involved due to the use of eigen functions of harmonically vibrating Euler-Bernoulli as the basis functions. This reduction in computational work is achieved because of the orthogonal properties of the eigen functions.

(iv) Kantorovich method is useful in the manual solution of thin plate problems.

Kantorovich method has been used in the literature to solve thin plate flexure problems. Ike [18] used the Kantorovich method to solve the thin plate flexure problem with fixed edge at $y =$ 0 and simple supports at $x =$ 0, $x = a$ , $y = b$ for the case of uniform load. Nwoji et al. [17] used the Kantorovich-Vlasov method to solve the flexural problem of simply supported Kirchhoff-Love plates under uniformly distributed load on the entire plate domain.

3. Research aim and objectives

The general aim is to use the Kantorovich variational method to solve the flexural problem of Kirchhoff-Love plates with CSCS edges for the case of uniformly distributed transverse load. The specific objectives include:

(i) To present the flexural Kirchhoff-Love plate problem as a variational problem and write the total potential energy functional.

(ii) To apply the Kantorovich variational technique in choosing suitable deflection functions in terms of one unknown coordinate function of the inplane variables.

(iii) To express the total potential energy functional in terms of the unknown function.

(iv) To use the Euler-Lagrange differential equations to write the equation of equilibrium of the plate.

(v) To solve the Euler-Lagrange differential equations, and thus obtain $f_{n} (x)$ that ensures the equilibrium of the plate.

(vi) To apply the conditions for symmetry of deflection and the boundary conditions to fully determine the unknown integration constants, and thus fully determine $f_{n} (x)$ .

(vii) To obtain the bending moments $M_{x x}$ , $M_{y y}$ from the bending moment displacement relations.

(viii) To obtain deflection and bending moment expressions for the center of the plate and bending moment values at the middle of the clamped plate.

4. Methodology/application of the Kantorovich variational method

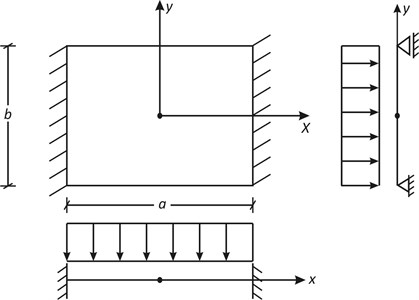
A uniformly loaded rectangular Kirchhoff-Love plate, $a \times b$ , simply supported on the edges $y = \pm b / 2$ , and clamped on the opposite edges $x = \pm a / 2$ , as shown in Fig. 1 was considered.

The plate is subject to a uniformly distributed transverse load of intensity $p$ over the entire plate domain, $R$ defined by $- a / 2 \leq x \leq a / 2$ , $- b / 2 \leq y \leq b / 2$ . The origin of the Cartesian coordinates system is chosen at the plate center, and the $x$ – and $y$ – coordinate axes are chosen to be parallel to the plate edges as shown in Fig. 1. This choice of Cartesian coordinates takes maximal advantage of the symmetry of the plate and the symmetry of the loading.

By the Kantorovich variational method, the deflection function $w (x, y)$ is represented as a single series of infinite terms involving variable – separable functions of the inplane coordinates $x$ , and $y$ , as follows:

1

w (x, y) = \sum_{n = 1}^{\infty} f_{n} (x) g_{n} (y) .

Fig. 1Uniformly loaded rectangular Kirchhoff-Love plate with clamped edges at y=± a/2, and simply supported edges at y=± b/2

The assumption of $w (x, y)$ in the form of Eq. (1) as a single series of infinite term is deliberate in order to seek an exact solution to the flexural problem of the Kirchhoff-Love plate. In the Kantorovich variational method, one of the functions is determined using the restraint and loading boundary conditions along either the x or the y coordinate directions.

In this work, the expected symmetrical deformation about $y =$ 0 and the boundary conditions at $y = \pm b / 2$ for $g_{n} (y)$ suggest that a suitable shape function in the $y$ direction is:

2

g_{n} (y) = c o s \frac{n π y}{b}, n = 1, 3, 5, 7, \dots .

Since $g_{n} (y)$ satisfies all the boundary conditions at $y = \pm b / 2$ . Then:

3

w (x, y) = \sum_{n = 1}^{\infty} f_{n} (x) c o s \frac{n π y}{b}, n = 1, 3, 5, 7, \dots,

where $f_{n} (x)$ is an unknown function of $x$ we seek to determine such that $w (x, y)$ minimizes the total potential energy functional for the Kirchhoff-Love plate and also satisfies the boundary conditio0ns at the clamped edges $(x = \pm a / 2)$ of the plate for each term of the infinite series.

The total potential energy functional $Π$ for the Kirchhoff-Love plate under flexural deformation is the sum of the strain energy in flexure and the potential energy of the applied transverse loads. Thus:

4

Π = U + V,

5

Π = \frac{1}{2} \iint_{R} D \{(\nabla^{2} w)^{2} - 2 (1 - μ) (w_{x x} w_{y y} - w_{x y}^{2})\} d x d y - \iint_{R} p (x, y) w (x, y) d x d y,

where $μ$ is the Poisson’s ratio, also:

6

w_{x x} = \frac{\partial^{2} w}{\partial x^{2}},

7

w_{y y} = \frac{\partial^{2} w}{\partial y^{2}},

8

w_{x y} = \frac{\partial^{2} w}{\partial x \partial y},

and $D$ is the flexural rigidity of the plate:

9

D = \frac{E h^{3}}{12 (1 - μ^{2})},

and $E$ is the Young’s modulus of elasticity, $h$ is the plate thickness, $\nabla^{2}$ is the Laplacian in $x$ , $y$ coordinates.

For the Kirchhoff-Love plate considered, the total potential energy functional simplifies further since the Gaussian curvature is zero for CSCS plates considered. Thus:

10

Π = \frac{1}{2} \iint_{R} D (\nabla^{2} w)^{2} d x d y - \iint_{R} p w d x d y,

since for CSCS thin plates:

11

w_{x x} w_{y y} - w_{x y}^{2} = 0 .

Eq. (10) is also expressed as Eq. (12):

12

Π = \iint_{R} \{\frac{D}{2} {((\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}) w (x, y))}^{2} - p w (x, y)\} d x d y .

Substitution of Eq. (3) into Eq. (12) yields Eq. (13):

13

Π = \iint_{} \{\frac{D}{2} {((\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}) \sum_{n = 1}^{\infty} f_{n} (x) c o s \frac{n π y}{b})}^{2} - p \sum_{n = 1}^{\infty} f_{n} (x) c o s \frac{n π y}{b}\} d x d y .

Simplification of Eq. (13) yields Eq. (14):

14

Π = \sum_{n = 1}^{\infty} \int_{- a / 2}^{a / 2} \int_{- b / 2}^{b / 2} \{\frac{D}{2} {(f_{n}^{''} (x) c o s \frac{n π y}{b} - f_{n} {(\frac{n π}{b})}^{2} c o s \frac{n π y}{b})}^{2} - p f_{n} (x) c o s \frac{n π y}{b}\} d y d x,

where primes denote differentiation (derivative) with respect to $x$ .

Further simplification of Eq. (14) yields Eq. (15):

15

Π = \sum_{n = 1}^{\infty} \int_{- a / 2}^{a / 2} \int_{- b / 2}^{b / 2} \{(\frac{D}{2} ((f_{n}^{''} (x))^{2} c o s^{2} \frac{n π y}{b} - 2 {f''}_{n} (x) f_{n} (x) {(\frac{n π}{b})}^{2} c o s^{2} \frac{n π y}{b} + {(\frac{n π}{b})}^{4} c o s^{2} \frac{n π y}{b})) - p f_{n} (x) c o s \frac{n π y}{b}\} d y d x .

From Eq. (15), evaluation of the integration with respect to $y$ simplifies the total potential energy functional to Eq. (16):

16

Π = \frac{b}{2} \int_{- a / 2}^{a / 2} \{((f_{n}^{''} (x))^{2} - 2 {(\frac{n π}{b})}^{2} f_{n}^{''} (x) f_{n} (x) + {(\frac{n π}{b})}^{4} f_{n} (x)) - (- 1)^{\frac{n - 1}{2}} \frac{8 p}{n π D} f_{n} (x)\} d x = \frac{b}{2} \int_{- a / 2}^{a / 2} F (x, f_{n} (x), {f''}_{n} (x)) d x .

The Euler-Lagrange differential equations for the functional Eq. (16) is obtained from Eq. (17):

17

\frac{\partial F}{\partial f_{n} (x)} - \frac{d}{d x} (\frac{\partial F}{\partial {f^{'}}_{n} (x)}) + \frac{d^{2}}{d x^{2}} (\frac{\partial F}{\partial {f^{''}}_{n} (x)}) = 0 .

The Euler-Lagrange differential equation is obtained as the fourth order ordinary differential equation, ODE, Eq. (18):

18

f_{n}^{i v} (x) - 2 {(\frac{n π}{b})}^{2} f_{n}^{''} (x) + {(\frac{n π}{b})}^{4} f_{n} (x) = (- 1)^{\frac{n - 1}{2}} \frac{4 p}{D n π}, n = 1, 3, 5, 7, \dots .

The general solution to Eq. (18) is given by Eq. (19):

19

f_{n} (x) = (A_{n}^{*} s i n h \frac{n π x}{b} + B_{n}^{*} \frac{n π x}{b} c o s h \frac{n π x}{b})

+ C_{n}^{*} c o s h \frac{n π x}{b} + D_{n}^{*} \frac{n π x}{b} s i n h \frac{n π x}{b} + (- 1)^{\frac{n - 1}{2}} \frac{4 p b^{4}}{(n π)^{5} D},

where $A_{n}^{*}$ , $B_{n}^{*}$ , $C_{n}^{*}$ and $D_{n}^{*}$ are the four constants of integration.

For symmetry about $x =$ 0:

20

A_{n}^{*} = B_{n}^{*} = 0,

and the general solution for $f_{n} (x)$ becomes Eq. (21):

21

f_{n} (x) = C_{n} c o s h \frac{n π x}{b} + D_{n} x s i n h \frac{n π x}{b} + (- 1)^{\frac{n - 1}{2}} \frac{4 p b^{4}}{D (n π)^{5}},

where:

22

C_{n} = C_{n}^{*},

23

D_{n} = D_{n}^{*} (\frac{n π}{b}) .

The boundary conditions at the clamped edges, given by Eqs. (24) and (25) are applied to Eq. (21):

24

f_{n} (x = \pm \frac{a}{2}) = 0,

25

{f'}_{n} (x = \pm \frac{a}{2}) = 0 .

Enforcement of boundary conditions yield Eq. (26):

26

D_{n} = \frac{4 p b^{4} (- 1)^{\frac{n - 1}{2}}}{D (n π)^{5} G_{n}},

where:

27

G_{n} = \frac{b}{n π} c o s h \frac{n π a}{2 b} + \frac{a}{2 s i n h \frac{n π a}{2 b}},

28

G_{n} = (\frac{b}{n π} c o s h \frac{n π r}{2} + \frac{a}{2 s i n h \frac{n π r}{2}}),

where:

29

r = \frac{a}{b},

30

C_{n} = - D_{n} (\frac{b}{n π} + \frac{a}{2 t a n h \frac{n π r}{2}}) = - D_{n} b (\frac{1}{n π} + \frac{r}{2 t a n h \frac{n π r}{2}}) .

Thus, $w (x, y)$ is fully determined using Eq. (3).

5. Results

5.1. Center deflection

The centre deflection $w (0,0)$ is obtained as Eq. (31):

31

w (0,0) = \sum_{n = 1}^{\infty} (C_{n} + (- 1)^{\frac{n - 1}{2}} \frac{4 p b^{4}}{D (n π)^{5}}) .

5.2. Bending moments

The bending moment displacement equations – Eqs. (32) and (33) – are used to obtain the bending moments at the centre and at the middle of the clamped edges. Thus from:

32

M_{x x} = - D (w_{x x} + μ w_{y y}),

33

M_{y y} = - D (w_{y y} + μ w_{x x}) .

The bending moments at the plate centre are obtained as Eqs. (34) and (35):

34

M_{x x} (0,0) = - D \{\sum_{n = 1}^{\infty} ({(\frac{n π}{b})}^{2} C_{n} + \frac{2 n π}{b} D_{n}) - μ \sum_{n = 1}^{\infty} {(\frac{n π}{b})}^{2} (C_{n} + (- 1)^{\frac{n - 1}{2}} \frac{4 p b^{4}}{D (n π)^{5}})\},

35

M_{y y} (0,0) = - D \{- \sum_{n = 1}^{\infty} {(\frac{n π}{b})}^{2} (C_{n} + (- 1)^{\frac{n - 1}{2}} \frac{4 p b^{4}}{D (n π)^{5}}) + μ \sum_{n = 1}^{\infty} ({(\frac{n π}{b})}^{2} C_{n} + \frac{2 n π}{b} D_{n})\} .

The bending moments at the middle of the clamped edge $(x = a / 2, y = 0)$ are obtained as Eqs. (36) and (37):

36

M_{x x} (\frac{a}{2}, 0) = - D \{\sum_{n = 1}^{\infty} ({(\frac{n π}{b})}^{2} C_{n} c o s h \frac{n π a}{2 b}) + D_{n} (\frac{2 n π}{b} c o s h \frac{n π a}{2 b} + {(\frac{n π}{b})}^{2} \frac{a}{2} s i n h \frac{n π a}{2 b})

- μ \sum_{n = 1}^{\infty} (C_{n} c o s h \frac{n π a}{2 b} + D_{n} \frac{a}{2} s i n h \frac{n π a}{2 b} + (- 1)^{\frac{n - 1}{2}} \frac{4 p b^{4}}{D (n π)^{5}}) {(\frac{n π}{b})}^{2}\},

37

M_{y y} (\frac{a}{2}, 0) = - D \{- \sum_{n = 1}^{\infty} (C_{n} c o s h \frac{n π a}{2 b} + \frac{D_{n} a}{2} s i n h \frac{n π a}{2 b} + \frac{(- 1)^{\frac{n - 1}{2}} 4 p b^{4}}{D (n π)^{5}}) {(\frac{n π}{b})}^{2}

+ μ (\sum_{n = 1}^{\infty} ({(\frac{n π}{b})}^{2} C_{n} c o s h \frac{n π a}{2 b} + D_{n} (2 (\frac{n π}{b}) c o s h \frac{n π a}{2 b} + {(\frac{n π}{b})}^{2} \frac{a}{2} s i n h \frac{n π a}{2 b})))\} .

From Eq. (31) the centre deflection is calculated for $n =$ 1, $r =$ 1, as Eq. (38):

38

w (0,0) = 0.001961886 \frac{p a^{4}}{D} = 1.961886 \times 1 0^{- 3} \frac{p a^{4}}{D} .

For $n =$ 3, $r =$ 1, the centre deflection is calculated as Eq. (39):

39

w (0,0) = 1.913609 \times 1 0^{- 3} \frac{p a^{4}}{D} .

For $n =$ 5, $r =$ 1, the centre deflection is calculated as Eq. (40):

40

w (0,0) = 1.917753 \times 1 0^{- 3} \frac{p a^{4}}{D} .

The exact solution for the centre deflection of square Kirchhoff-Love plates is given by Eq. (41):

41

W_{e x a c t} = 1.92 \times 1 0^{- 3} \frac{p a^{4}}{D} .

The use of Eqs. (34) and (35) for obtaining the centre bending moments give: for square Kirchhoff-Love plates: For $n =$ 1, $r =$ 1:

42

M_{x x} (0,0) = 0.034615 p a^{2} .

For $n =$ 3, $r =$ 1:

43

M_{x x} (0,0) = 0.03301 p a^{2} .

For $n =$ 1, $r =$ 1:

44

M_{y y} (0,0) = 0.028005 p a^{2} .

For $n =$ 3, $r =$ 1:

45

M_{y y} (0,0) = 0.0236212 p a^{2} .

Convergence to the exact bending moment values is achieved for $n =$ 7.

6. Discussion

The Kantorovich variational method was successfully applied in this study to the flexural problem of Kirchhoff-Love plate subjected to uniformly distributed transverse load over the entire plate domain. The problem was expressed in variational form as the problem of finding the deflection $w (x, y)$ that minimizes the total potential energy functional given as Eq. (5). Kantorovich procedure was adopted to express the unknown deflection $w (x, y)$ in terms of two variable separable functions $f_{n} (x)$ and $g_{n} (y)$ such that one of the functions is chosen to aprori satisfy all the boundary conditions along the corresponding coordinate direction; while the other function remained unknown. The expected symmetrical nature of the deflection about the $y =$ 0 axis, and the need to obtain exact solutions within the Kirchhoff-Love theory led to the choice of the deflection function in single infinite series form as Eq. (3).

Substitution of Eq. (3) into the total potential energy functional and integration with respect to $y$ simplified the functional as Eq. (16). The integration in Eq. (16) was found to depend on $x$ , $f_{n} (x)$ and $f_{n}^{'} (x) .$ The conditions for equilibrium of the Kirchhoff plate, represented by the Euler-Lagrange differential equation – Eq. (16) – was applied to obtain the equation of equilibrium as the fourth order ordinary linear differential equation given by Eq. (18). The general solution given as Eq. (19) was obtained using the method of trial functions, undetermined parameters, $D$ operator or variation of parameters as the linear superposition of the homogenous and the particular solution. The four constants of integration in the general solution (for each $n$ ), were obtained using theconsiderations of symmetry of $f_{n} (x)$ about $x =$ 0, and the restraint and loading boundary conditions at the clamped edges ( $x = \pm a / 2$ ). The deflection function was thus completely determined with the determination of the constants of integration. The centre deflection was obtained as Eq. (31). The bending moments $M_{x x}$ and $M_{y y}$ at the plate centre were found as Eqs. (34) and (35) respectively. The bending moments at the middle of the clamped edge ( $x = \pm a / 2$ , $y =$ 0) were found as Eqs. (36) and (37).

The solutions for deflection and bending moments were obtained as single series of infinite terms involving hyperbolic functions and depending on $a / b$ , the aspect ratio of the plate. Numerical values of the converged deflection coefficients and bending moment coefficients at the centre of the plate were evaluated for given values of the plate aspect ratio and presented in Table 1 together with similar values obtained by Timoshenko and Woinowsky-Krieger [11] and Cui-Shuang [12], for purposes of comparison and validation.

A comparison of the results for the centre deflection coefficients and bending moments coefficients $β_{x x}$ and $β_{y y}$ show that the Kantorovich-variational method gives the exact solutions at convergence. Convergence studies show that the single series for the centre deflection and centre bending moments are rapidly convergent as sufficient convergence to the exact solutions result with the use of three terms of the series.

Table 1Deflection and bending moment coefficients for a uniformly loaded CSCS Kirchhoff-Love plate with μ= 0.30

$\frac{a}{b}$	Deflection $(\times 1 0^{- 3} \frac{p b^{4}}{D})$			Bending moment $β_{x x} (\times 1 0^{- 2} p b^{2})$			Bending moment coefficients $β_{y y}$ $(\times 1 0^{- 2} p b^{2})$ .
	Timoshenko and Woinowsky- Krieger	Cui Shuang	Present study	Timoshenko and Winowsky- Krieger	Cui Shuang	Present study	Timoshenko and Winowsky-Krieger	Cui Shuang	Present study
1/2	2.60	2.61079	2.6108	1.42	1.41716	1.4172	4.20	4.20629	4.2063
2/3	2.47	2.4757	2.4757	1.79	1.78003	1.78	4.06	4.06276	4.0628
1	1.92	1.91714	1.9171	2.44	2.43874	2.4387	3.32	3.32449	3.3245
3/2	5.31	5.32645	5.3265	5.85	5.84803	5.858	4.60	4.59444	4.5944
2	8.44	8.445	8.445	8.69	8.6868	8.6868	4.74	4.73622	4.7362

The major contributions of this study are as follows:

(i) The study gave an exact solution (Eq. (31)) for the deflection at the centre of uniformly loaded Kirchhoff-Love plates clamped at two opposite edges $x = \pm a / 2$ , and simply supported at the other two edges $y = \pm b / 2$ . The solution is a single series of infinite terms with rapidly converging properties. Sufficient accuracy and convergence is achieved by the use of three terms of the series for centre deflection, $w (0,0)$ . Exact solutions are achieved with five terms of the series for $w (0,0)$ .

(ii) The study gave exact solutions for the bending moments at the centre $M_{x x} (0,0)$ and $M_{y y} (0,0)$ of uniformly loaded Kirchhoff-Love plates with clamped edges ( $x = \pm a / 2$ ) and simply supported edges ( $y = \pm b / 2$ ) as Eqs. (34) and (35) respectively. The centre bending moments were rapidly converging single series of infinite terms. Sufficient convergence to the exact solutions were obtained using five terms of the series.

(iii) The study presented exact solutions for the bending moments at the middle of the clamped edges $M_{x x}$ ( $x = \pm a / 2$ , $y =$ 0) and $M_{y y}$ ( $x = \pm a / 2$ , 0) as Eqs. (36) and (37). The expressions were similarly single series of infinite terms.

7. Conclusions

From the study, the following conclusions are made:

(i) The Kantorovich variational method is an effective technique for solving the flexural problem of Kirchhoff-Love plates with CSCS edges and under uniform transverse load.

(ii) The Kantorovich variational method gives solutions for deflections that are single series of infinite terms.

(iii) The solutions for deflections obtained are rapidly convergent and converge to the exact solutions with the use of three terms of the infinite series.

(iv) The solutions obtained for bending moments are also single series of infinite terms containing hyperbolic functions. The single series expressions for the bending moments are similarly rapidly convergent, yielding exact solutions with four terms of the series.

References

Introduction to Plate bending Problems. Indian Institute of Technology Kharagpur, www.nptel.ac.in/courses/105105041/module%206.pdf.

Search CrossRef
Kelly P. A. Mechanics Lecture Notes: an Introduction to Solid Mechanics, http://homepages.engineering.auckland.ac.nz/~pkel015/SolidMechanicsBooks/index.html.

Search CrossRef
Ike C. C. Equilibrium method in the derivation of differential equations for homogeneous isotropic Mindlin plates. Nigerian Journal of Technology, Vol. 36, Issue 2, 2017, p. 346-350.

Publisher
Nwoji C. U., Onah H. N., Mama B. O., Ike C. C. Theory of elasticity formulation of the Mindlin plate equations. International Journal of Engineering and Technology, Vol. 9, Issue 6, 2017, p. 4344-4352.

Publisher
Ike C. C., Nwoji C. U., Ofondu I. O. Variational formulation of Mindlin plate equation and solution for deflection of clamped Mindlin plates. International Journal for Research in Applied Sciences and Engineering Technology, Vol. 5, Issue 1, 2017, p. 340-353.

Search CrossRef
Nwoji C. U., Ikwueze E. U., Ofondu I. O. Bending analysis of simply supported Kirchhoff plates under linearly distributed transverse load. Explorematics Journal of Innovative Engineering and Technology, Vol. 1, Issue 1, 2017, p. 28-36.

Search CrossRef
Onah H. N., Mama B. O., Ike C. C., Nwoji C. U. Kantorovich-Vlasov method for the flexural analysis of Kirchhoff plates with opposite edges clamped and simply supported (CSCS plates). International Journal of Engineering and Technology, Vol. 9, Issues 6, 2017, p. 4333-4343.

Publisher
Nwoji C. U., Mama B. O., Ike C. C., Onah H. N. Galerkin-Vlasov method for the flexural analysis of rectangular Kirchhoff plates with clamped and simply supported edges. IOSR Journal of Mechanical and Civil Engineering, Vol. 14, Issues 2, 2017, p. 61-74.

Publisher
Reissner E. The effect of transverse shear deformation on the bending of elastic plates. Journal of Applied Mechanics, Vol. 12, 1945, p. 69-77.

Publisher
Mindlin R. D. Influence of rotary inertia and shear on flexural motions of isotropic elastic plates. Journal of Applied Mechanics, Vol. 18, Issue 1, 1951, p. 31-38.

Publisher
Shimpi R. P. Refined plate theory and its variants. AIAA Journal, Vol. 40, 2002, p. 137-146.

Publisher
Chandrashekhara K. Theory of Plates. University Press, India, 2001.

Search CrossRef
Timoshenko S., Woinowsky Krieger Theory of Plates and Shells. 2nd Edition, McGraw Hill Book Co., New York, 1959.

Search CrossRef
Cui Shuang Symplectic Elasticity Approach for Exact Bending Solution of Rectangular Thin Plates. Master Thesis, City University of Hong Kong, 2007.

Search CrossRef
Mama B. O., Nwoji C. U., Ike C. C., Onah H. N. Analysis of simply supported rectangular Kirchhoff plates by the finite Fourier sine transformation method. International Journal of Advanced Engineering Research, Vol. 4, Issue 3, 2017, p. 285-291.

Publisher
Osadebe N. N., Ike C. C., Onah H., Nwoji C. U., Okafor F. O. Application of the Galerkin-Vlasov Method to the flexural analysis of simply supported rectangular Kirchhoff plates under uniform loads. Nigerian Journal of Technology, Vol. 35, Issue 4, 2016, p. 732-738.

Publisher
Nwoji C. U., Mama B. O., Onah H. N., Ike C. C. Kantorovich-Vlasov method for simply supported plates under uniformly distributed load. International Journal of Civil, Mechanical and Energy Science, Vol. 3, Issue 2, 2017, p. 69-77.

Publisher
Ike C. C. Kantorovich-Euler Lagrange-Galerkin method for bending analysis of thin plates. Nigerian Journal of Technology, Vol. 36, Issue 2, 2017, p. 351-360.

Publisher
Aginam C. H., Chidolue C. A., Ezeagu C. A. Application of direct variational method in the analysis of isotropic thin rectangular plates. ARPN Journal of Engineering and Applied Sciences, Vol. 7, Issue 9, 2012, p. 1128-1138.

Search CrossRef
Eze J. C., Ibearugbulem O. M., Onyechere C. I. Pure bending analysis of thin rectangular flat plates using ordinary finite difference method. International Journal of Emerging Technology and Advanced Engineering, Vol. 3, Issue 3, 2013, p. 20-23.

Search CrossRef
Navier C. L. M. N. Extrait des recherché sur la flexion des plans elastiques. Bulletin Des Science, Par La Societe Philomatique De Paris, Vol. 5, 1823, p. 95-102.

Search CrossRef
Szilard R. Theories and Applications of Plate Analysis: Classical Numerical and Engineering Methods. John Wiley and Son Inc, 2004.

Publisher
Levy M. Memoire sur la theorie des plaques elastiques planes. Journal De Mathematiques Pures Et Appliquees, Vol. 30, 1899, p. 219-306.

Search CrossRef
Tian B., Zhong Y., Li R. Analytic bending solutions of rectangular cantilever thin plates. Archives of Civil and Mechanical Engineering, Vol. 11, Issue 4, 2011, p. 1043-1052.

Publisher
Johnarry T. N. Acceleration displacement ratio transform of differentials for transverse plates and constant stiffness buckling solution. Innovative Systems Design and Engineering, Vol. 2, Issue 4, 2011, p. 250-263.

Search CrossRef
Balasubrainanian Ashwin Plate Analysis with Different Geometries and Arbitrary Boundary Conditions. M.Sc. Thesis, Faculty of the Graduate School, University of Texas at Arlington, 2011.

Search CrossRef
Kaliakin V. N. Introduction to Approximate Solution Techniques, Numerical Modelling and Finite Element Methods. Marcell Dekker Inc., New York, USA, 2002.

Search CrossRef

Cited by

An Approximation Solution of Linear Differential Equation using Kantorovich Methods

Wasan Ajeel Ahmood | Marwa Mohamed Ismaeel

(2023)

Alternative surface treatments for the repair of through-wall corrosion damage in metallic pipes with bonded plates

M.J. Oliveira | F.F. Enne | J.M.L. Reis | H.S. da Costa Mattos

(2022)

Computing static behavior of flexible rectangular von Kármán plates in fast and reliable way

J. Awrejcewicz | V.A. Krysko | L.A. Kalutsky | V.A. Krysko

(2022)

Review of the Methods of Transition from Partial to Ordinary Differential Equations: From Macro- to Nano-structural Dynamics

J. Awrejcewicz | V. A. Krysko | L. A. Kalutsky | M. V. Zhigalov | V. A. Krysko

(2021)

Generalized Integral Transform Method for Bending and Buckling Analysis of Rectangular Thin Plate with Two Opposite Edges Simply Supported and Other Edges Clamped

Charles Chinwuba Ike | Michael Ebie Onyia | Eghosa Oluwaseyi Rowland-Lato

(2021)

About this article

Received

16 February 2018

Accepted

13 March 2018

Published

31 March 2018

DOI

https://doi.org/10.21595/mme.2018.19750

Keywords

Kantorovich variational method

Kirchhoff-Love plate

total potential energy functional

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 02 22

Galerkin-Kantorovich variational method for solving saint venant torsion problems of rectangular bars

Charles Chinwuba Ike

Research article

2024 02 20

Solving Saint Venant torsion problems for rectangular beams using single finite Fourier sine transform method

Charles Chinwuba Ike

Research article

2019 11 28

Free vibration analysis of simply supported rectangular plates

Ganesh Naik Guguloth, Baij Nath Singh, Vinayak Ranjan

Research article

2018 12 13

Comparison of natural frequencies of isotropic plate using DSM with Wittrick-Williams algorithm

Manish Chauhan, Vinayak Ranjan, Baij Nath Singh

C. C. Ike and B. O. Mama, “Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates,” Mathematical Models in Engineering, Vol. 4, No. 1, pp. 29–41, Mar. 2018, https://doi.org/10.21595/mme.2018.19750

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/mme.2018.19750
UR  - https://doi.org/10.21595/mme.2018.19750
TI  - Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates
T2  - Mathematical Models in Engineering
AU  - Ike, Charles Chinwuba
AU  - Mama, Benjamin Okwudili
PY  - 2018
DA  - 2018/03/31
PB  - JVE International Ltd.
SP  - 0-0
IS  - 1
VL  - 4
SN  - 2351-5279
SN  - 2424-4627
ER  - 

Copy Ris

Copied to clipboard!

@article{Ike_2018,
	doi = {10.21595/mme.2018.19750},
	url = {https://doi.org/10.21595/mme.2018.19750},
	year = 2018,
	month = {mar},
	publisher = {{JVE} International Ltd.},
	volume = {4},
	number = {1},
	pages = {0--0},
	author = {Charles Chinwuba Ike and Benjamin Okwudili Mama},
	title = {Kantorovich variational method for the flexural analysis of {CSCS} Kirchhoff-Love plates},
	journal = {Mathematical Models in Engineering}
}

Copy Bibtex

Copied to clipboard!

[1]C. C. Ike and B. O. Mama, “Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates,” Mathematical Models in Engineering, vol. 4, no. 1, pp. 0–0, Mar. 2018, doi: 10.21595/mme.2018.19750.

Copy IEEE

Copied to clipboard!

Ike, Charles Chinwuba, and Benjamin Okwudili Mama. “Kantorovich Variational Method for the Flexural Analysis of CSCS Kirchhoff-Love Plates.” Mathematical Models in Engineering 4, no. 1 (March 31, 2018): 0–0. https://doi.org/10.21595/mme.2018.19750.

Copy Chicago

Copied to clipboard!

Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates

Abstract

1. Introduction

2. Review of plate theories

2.1. Review of methods of solving thin plate bending problems

2.2. Advantages of the Kantorovich variational method

3. Research aim and objectives

4. Methodology/application of the Kantorovich variational method

5. Results

5.1. Center deflection

5.2. Bending moments

6. Discussion

7. Conclusions

References

Cited by

About this article

Related Articles