Abstract
In order to achieve the non-stationary de-noising signal effectively, and to solve the prediction of less sample, a hybrid model composed of FCCA (Fuzzy C-means clustering algorithm) and FOM (Fractional Order Model) was constructed. The degree of each data point was determined by FCCA to de-noise and the order cumulative matrix was extended to fractional cumulative matrix, so that the fractional order cumulative grey model was established to make forecasting. The results of numerical example showed that the hybrid model can obtain better prediction accuracy.
1. Introduction
In the analysis of vibration abrasion, noise factor is a significant aspect to reduce the prediction accuracy. In order to discard noise in signal, scholars domestic and abroad have carried on many years of research, and the de-noising methods such as Fourier transform [1-3] and wavelet transform [4, 5] were proposed. However, although the stationary signal can be de-noised by Fourier transform well, but this method can hardly identify the high frequency part and noise of the signal, which is not conducive to the analysis of non-stationary signals. Compared with the Fourier transform, the wavelet transform can improve the performance of de-noising of non-stationary nonlinear time-varying signals, but the effect of wavelet filtering is unsatisfactory when the noise is large, or the energy is limited, and also the wavelet basis is not easy to select.
For improving the situation mentioned above, a fuzzy C-means clustering algorithm was established. After distinguishing large scale noise and sharp features, fuzzy C-means clustering algorithm was utilized to cluster the sharp features and obtain more accurate data. Besides, considering the characteristics of less samples, the fractional order cumulative model was established to reduce the perturbation bounds and improve the stability of the prediction model.
2. Fuzzy C-means clustering algorithm
Fuzzy C-mean clustering (FCM) is a method which utilizes the membership degree to determine the degree of each data point belonging to a certain cluster. A set of data can be divided into two or more cluster centers by FCM. Suppose that is a set of data points with dimensional which containsdata points. Then the set can be divided into clusters: , where is center of the cluster. Thus, the objective function of the fuzzy C-means clustering algorithm is defined as:
where:
– The membership degree of data point relative to cluster center ;
– Fuzzy control degree parameter;
– Euclidean distance between data point and cluster center , and .
The constraints of Eq. (1) are as follows:
In order to reflect the influence of different data points, the improved fuzzy clustering method was established, which defined the fuzzy weight coefficient of fuzzy weight distance, based on the different contribution of different data points to the same cluster center. And then the distance between the data points and the cluster centers is defined as:
In contrast, the fuzzy weight coefficient makes the distance farther more farther and closer, which can reduce the influence of noise, and make the clustering results better.
The basic steps of the algorithm are as follows:
1) Set the radius of the bounding sphere is , and the threshold of the number of data points in the sphere is determined according to the density of the point cloud;
2) Select a data point and calculate the number of the adjacent points in the sphere enclosed of which the center is and the radius is ;
3) Compare the number of data in sphere enclosed and the threshold value , if , the data point would be determined as noise and deleted directly;
4) If the data point is regarded as the qualified point, the improved FCM algorithm is utilized to cluster the enclosing sphere contains . Meanwhile, the data in the cluster is recorded, and all data in the sphere will be replaced by the data of the cluster center;
5) Return to step (2) and determine the remaining points in turn.
3. Fractional order model
In order to define the fractional order operation, the ascending order function was introduced:
where 1.
The fractional cumulative grey model is obtained after making the order of extended to the general positive real number . Then can be obtained by combining with Eq. (1):
Make extended to which is general positive real number and . The order cumulative generating series can be defined as:
When , is fractional order accumulation, which can be written in matrix form:
where:
is fractional order cumulative matrix.
Similar to the integer order cumulative matrix, the transposed matrix of is a fractional Inverse cumulative matrix.
The reverse fractional order cumulative generation of series can be obtained by , then the reverse cumulative gray model can be established.
The discrete form of fractional order model can be expressed as:
where .
Because , so the is nonsingular matrices. Therefore, the exists, and , where is unit matrix.
4. Numerical example
As shown in Table 1, in order to verify the validity and reliability of the established hybrid model, the data from [6] was used as original signal for analyzing.
Table 1The original signal from 2007 to 2015
Time | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
Consumption | 33 | 35 | 25 | 34 | 38 | 31 | 26 | 35 | 36 |
4.1. Data analysis
According to Table 1, the original series shows non-stationary characteristics. In order to test the prediction ability of established model, the consumption from 2007 to 2014 were utilized as input to forecast consumption in 2015.
4.2. Simulation
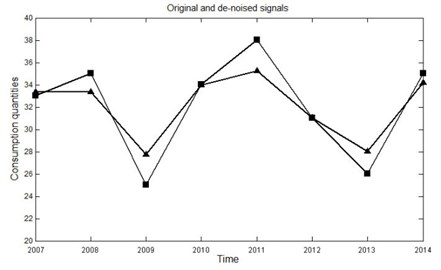
In order to eliminate the influence of noise in the series, the original data was utilized as input to Fuzzy C-means clustering algorithm. Before the prediction, the residual was discarded, and the de-noised data were constructed by FCCA. The original data and the de-noised data were shown in Fig. 1.
Fig. 1The de-noised and original consumption data
The prediction model was established by fractional order grey model GM(,1) and the optimal order was 0.703, which calculated by genetic algorithm. And then the prediction results of de-noised signal were calculated. Moreover, for facilitate analyzing the predictive capabilities of FCCA-FOM, GM(1,1), FOM model and EWT-BP neural network were employed for comparison. The relative error and mean relative error(MRE) were utilized to measure the forecasting accuracy, and the results were shown in Table 2.
Table 2The prediction results and performance evaluations of forecasting results by different models
Time and MRE | Actual data | FCCA-FOM | GM(1,1) | FOM | EWT-BP neural network | ||||
Prediction data | Relative error/% | Prediction data | Relative error/% | Prediction data | Relative error/% | Prediction data | Relative error/% | ||
2007 | 33 | 32.1 | –2.73 | 35.9 | 8.79 | 36.7 | 11.21 | 34.6 | 4.85 |
2008 | 35 | 36.5 | 4.29 | 33.3 | –4.86 | 33.4 | –4.57 | 36.9 | 5.43 |
2009 | 25 | 25.9 | 3.60 | 27.1 | 8.40 | 26.5 | 6.00 | 26.3 | 5.20 |
2010 | 34 | 35.5 | 4.41 | 32.1 | –5.59 | 31.7 | –6.76 | 36.1 | 6.18 |
2011 | 38 | 39.4 | 3.68 | 40.3 | 6.05 | 39.8 | 4.74 | 36.4 | –4.21 |
2012 | 31 | 30.3 | –2.26 | 28.8 | –7.10 | 29.9 | –3.55 | 29.5 | –4.84 |
2013 | 26 | 27.5 | 5.77 | 28.9 | 11.2 | 29.1 | 11.92 | 27.6 | 6.15 |
2014 | 35 | 35.8 | 2.29 | 36.9 | 5.43 | 37.5 | 7.14 | 36.5 | 4.29 |
2015 | 36 | 36.9 | 2.50 | 38.6 | 7.22 | 38.8 | 7.78 | 37.7 | 4.72 |
MRE /% | 3.50 | 7.18 | 7.07 | 5.10 | |||||
4.3. Comparisons and discussion
According to the results of the Table 1, the relative error and the average relative error of FCCA-FOM are all smaller than the other 3 models, which can reflect the better accuracy and practicability of the model. Furthermore, it can be seen that the Fuzzy C-means clustering algorithm can effectively improve the prediction accuracy through comparison between FCCA-FOM and FOM.
5. Conclusions
Considering the noise in consumption series, a hybrid forecasting method combining FCCA and Fractional order was proposed, which can eliminate the noise in the original series and improve the prediction accuracy. At the same time, the method requires less data and no complicated integral calculation, which is easier to implement and convenient for engineering application. The numerical example showed that the relative error and average relative error of FCM-FOM model are less than GM(1,1), FOM and EWT-BP neural network, which reflect the accuracy of the model established.
References
-
Alieva T., Bastiaans M., Stankovic L. Signal reconstruction from two close fractional Fourier power spectra. IEEE Transactions on Signal Processing, Vol. 51, Issue 1, 2003, p. 112-123.
-
Zhu B. H., Liu S. T., Ran Q. W. Optical image encryption based on multi-fractional Fourier transforms. Optics Letters, Vol. 25, Issue 16, 2000, p. 1159-1161.
-
Ran Q., Yeung D., Tsang E., et al. General multi-fractional Fourier transform method based on the generalized permutation matrix group. IEEE Transactions on Signal Processing, Vol. 53, Issue 1, 2005, p. 83-98.
-
Catalao J. P. S., Pousinho H. M. I. VMF Mendes. Short-term wind power forecasting in Portugal by neural networks and wavelet transform. Renew Energy, Vol. 36, 2011, p. 1245-1251.
-
Partal Turgay, Kisi Ozgur Wavelet and neuro-fuzzy conjunction model for precipitation forecasting. Journal of Hydrology, Vol. 342, 2007, p. 199-212.
-
Zhou Hao, Huang Shanzhong Equipment consumption based on GM(1,1) and gray prediction Markov model. Journal of Wuhan University of Technology, Transportation Science and Engineering, Vol. 39, Issue 6, 2015, p. 1166-1168.
-
Zhao Jianzhong, Xu Tingxue, Liu Yong, et al. Consumption forecasting of missile spare parts based on rough set, entropy weight and improved SVM. Acta Armamentarii, Vol. 33, Issue 10, 2012, p. 1258-1265.
-
Zhou Yimin, Wang Qian, Yang Shuo The application of dynamic gray forecast model on the consumption rule of aviation ammunition spares. Logistics Science Technology, Vol. 7, 2017, p. 135-141.
-
Chen Yan, Wang Zijian, Zhao Ze, et al. Gaussian process modeling and multi-step prediction for time series data in wireless sensor network environmental monitoring. Journal on Communications, Vol. 36, Issue 10, 2015, p. 1-11.
-
Liang Lihua, Xun Panpan, Wang Baohua Shock response spectrum prediction of underwater explosion based on an ARMA model. Journal of Vibration and Shock, Vol. 32, Issue 13, 2013, p. 23-26.
-
Cheng Jinjun, Xia Zhixun, Hu Leigang Prognostics for aeronautic equipment based on genetic neural network. Journal of Air Force Engineering University: Natural Science Edition, Vol. 12, Issue 1, 2011, p. 15-19.
-
Qi Deqing, Li Weimin, Wang Huanxiang, et al. Prediction of the ballistic missile position information based on improved GM(1,1) model. Journal of Air Force Engineering University: Natural Science Edition, Vol. 13, Issue 1, 2012, p. 37-41.
-
Li Dawei, Zhang Zhihua, Liu Tianhua A regulated method of initial spare parts based on Bayes method. System Engineering Theory and Practice, Vol. 33, Issue 11, 2013, p. 2967-2971.
