Abstract
In order to separate multiple random fault source signals adaptively only from mixed vibration measurement signals of mechanical system in the situation of time-varying source signals and mixture system, two adaptive blind identification and separation methods are proposed to solve this kind of problem. One is based on recursive least squares (RLS) algorithm and another is based on recursive EASI algorithm. The simulation results show that both of these methods can separate source signals from the mixed signal in the situation of time-varying source signals and mixture system very well.
1. Introduction
In practice of mechanical fault diagnosis, fault characteristic information extracting is a very key link [1]. Due to the complexity of mechanical equipment structure, there is usually mixing and multipath effect for mechanical vibration signals. So, vibration measurement response signals of mechanical system are mixed signals of multiple source vibration of mechanical equipment structure, rather than real vibration source signals of specific components or position. In addition, the frequency of the vibration source signals may also interlap from each other, which makes fault characteristic information extraction much more difficultly. With the statistical independence among multiple random source signals, blind source separation (BSS) can makes the output close to the source signals as much as possible only from a set of mixed signals received by sensors when position, number of source signals and transmission channel parameters are unknown [2].
BSS is a good way for multiple random fault sources separation only from mixed vibration measurement response signals of mechanical system. BSS was firstly applied to fault diagnosis of gearbox by Ypma [3] in 1998. Now, it has been widely used in fault diagnosis of rolling element bearing, electromotor and engine [4]. And EASI [5] is one of the famous algorithms to solve BSS problem.
However, multiple random fault sources and mixture system are often time-varying in practice of mechanical. Chen [6] et al proposed a retrospective on-line EASI blind source separation algorithm to solve the time-varying system in practice of mechanical. Zhu [7] et al proposed a natural gradient-based recursive least squares algorithm for adaptive blind source separation, using this method the source signals can be separated on line. Based on these methods, this paper proposed RLS and R-EASI based methods to solve blind source separation in situation that both source signals and the system parameter are time-varying.
2. Theoretical inference of RLS and R-EASI for time-varying mixed BSS
2.1. Model of linear instantaneous mixing and time-varying mixed blind source separation
Without consideration of observation noise, the problem of linear instantaneous mixing and time-varying mixed blind source separation in situation of both sources and mixed matrix are time-varying can be expressed as follows [8-10]:
In Eq. (1), stands for measured signals (or mixed signals), stands for the number of mixed signals, is sampling time and is sampling length. stands for the linear instantaneous mixed matrix and it changes with time , stands for the source signals.
With consideration of observation noise:
where stands for the noise. And the goal of time-varying blind source separation is to find the appropriate time-varying separation matrix and let:
To make sure is an effective estimation of source signals .
Fig. 1Model of linear instantaneous time-varying mixed blind source separation
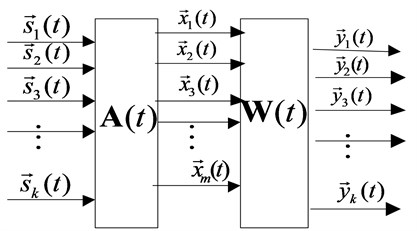
Actually, the BSS is a multiple solution problem, since for an observed signal , there may be an infinite group of mixing matrices when the source signals meet Eq. (2). So, to solve the problem valuably, we make two basic assumptions as below:
1) Mixing matrix is a column full rank matrix, presented as .
2) The source signal vector is a stationary random process with zero mean value, and the components of vector are statistically independent with no more than one component of obeying Gaussian distribution.
In absence of prior knowledge, there are two indeterminate problems about BSS problem:
1) The amplitude value of output signals is uncertain.
2) The order of output signals is uncertain.
3) The number of independent source signal vectors is uncertain.
If the contribution of independent source signal vectors is not enough, it is hard to identify and separate them. So, without any prior knowledge, determination of the number of independent source signal vectors by BSS algorithm is difficult.
The information in a signal is mainly contained in the waveform, and then how to recover the waveforms of each unknown source signal from mixed signal is the principal concern in blind source separation problems. And the original permutation of each signal and its real amplitude are the second concern. Indeed, both original permutation and real amplitude of the source signals are unsolvable in the case that only the mixed signals are available but the mixing matrix and source signals are unknown.
2.2. Theoretical inference of RLS for time-varying mixed BSS
The EASE algorithm is one of the widely used blind source separation algorithms [3], which uses the mutual information as the objective function and the natural gradient algorithm to optimize the separation matrix. The basic form of the iterative matrix is as follows [11]:
Where stands for learning step, is cost function and can be expressed as follows:
where expressed as nonlinear function. Unlike the batch gradient iterations of the least squares method, RLS can use natural gradient iterations and on-line processing which make it able to track system changes in the real-time.
2.3. Theoretical inference of R-EASI for time-varying mixed BSS
R-EASI has a low accuracy at the initial stage of separation. With the increase of the number of recursive, the accuracy of the separation matrix and separation sources are improved. After entering the tracking phase, the separation matrix and separation sources are basically the same. Therefore, it is necessary to find a separation matrix with higher separation accuracy in the tracking phase.
Due to the change of the system, it is necessary to find a suitable reference separation matrix for each mixed matrix to keep the mixed signal. We consider selecting a reference point between the current observation sample and the th observation sample, near the position of the current sample point. Let , where indicates rounding up, is a constant close to 1. In order to avoid the occurrence of large accidental errors in a separation matrix and make the separation effect worse, considering the selection of the reference point near the separation matrix as the basis of the separation matrix, as follows:
The th to observation samples are recursively recalculated using the baseline separation matrix :
And let .
3. Simulation verification
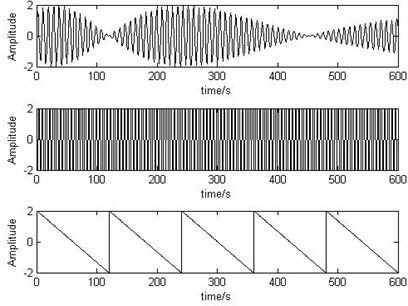
To verify the correctness of the two methods, the simulation is done. In the simulation, there are three source signals, one is rectangular wave, one is triangle wave and another is Sine wave and the amplitude changes with time as follows:
And the mixed matrix also changes with time, for convenience, only the first element of the matrix is time-varying. The time-invariant matrix should be generated randomly at first, and the first element changes with time as follows then:
The source signals, mixed signals and separated signals of recursive least squares (RLS) algorithm are shown as Fig. 2 to Fig. 4.
Fig. 2The time-varying source signals
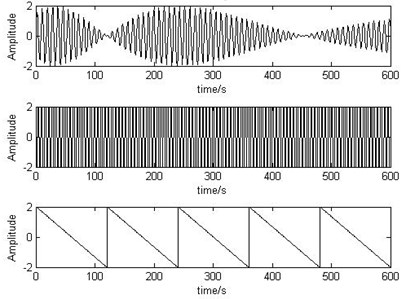
Fig. 3The mixed signals
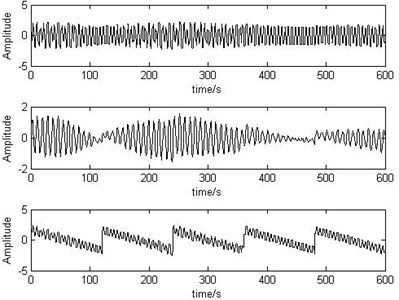
Fig. 4Output signals separated by recursive least squares
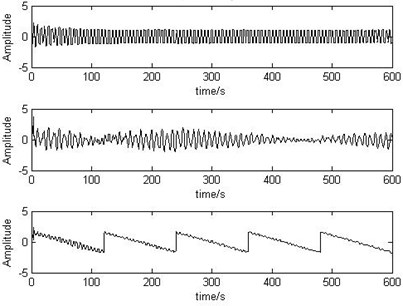
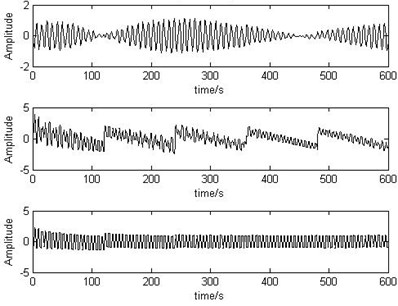
Fig. 5The time-varying source signals
The source signals, mixed signals and separated output signals of recursive EASI algorithm are shown as Fig. 5 to Fig. 7.
4. Conclusions
This paper proposes RLS and R-EASI based blind source separation algorithm in situation of both source signals and the system are time-varying. R-EASI improves the ability of the algorithm to track time-varying systems. How to ensure the convergence of optimization method and get higher precession are future reaches.
Fig. 6The mixed signals
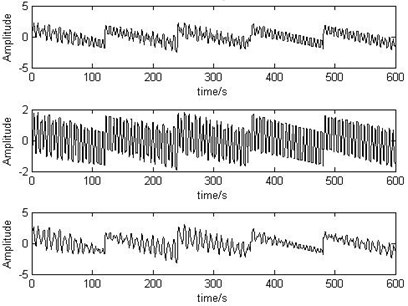
Fig. 7Output signals separated by recursive EASI
References
-
Mcfadden P. D., Smith J. D. Vibration monitoring of rolling element bearings by the high-frequency resonance technique – a review. Tribology International, Vol. 17, Issue 1, 1984, p. 3-10.
-
Li Z., Yan X., Tian Z., Yuan C., Peng Z., Li L. Blind vibration component separation and nonlinear feature extraction applied to the nonstationary vibration signals for the gearbox multi-fault diagnosis. Measurement, Vol. 46, Issue 1, 2013, p. 259-271.
-
Alexander Y. Learning methods for mechanical vibration analysis and health monitoring. Delft University of Technology Press, 1998, p. 15-16.
-
Cheng Wang, Jianying Wang, Bineng Zhong, et al. Negentropy and gradient iteration based fast independent component analysis for multiple random fault sources blind identification and separation. International Journal of Applied Electromagnetics and Mechanics, Vol. 52, Issues 1-2, 2016, p. 711-719.
-
Cardoso J.-F., Donoho D. L. Equivariant adaptive source separation. IEEE Transaction Signal Processing, Vol. 44, Issue 12, 1996, p. 3017-3030.
-
Chen H. P., Zhang H., Zhang J. Retrospective on-line EASI blind source separation algorithm. Journal of Signal Processing, Vol. 4, 2013, p. 24-31.
-
Zhu X., Zhang X., Ye J. Natural gradient-based recursive least-squares algorithm for adaptive blind source separation. Science in China, Vol. 47, Issue 1, 2004, p. 55-65.
-
Jiao L. C., Ma H. B., Liu F. Multiuser detector and independent component analysis: progress and natural gradient-based recursive least-squares algorithm for adaptive blind source separation prospective. Progress in Natural Science, Vol. 12, Issue 4, 2002, p. 365-371.
-
Feng D. Z., Bao Z., Zhang X. D. Multistage decomposition algorithm for blind source separation. Progress in Natural Science, Vol. 12, Issue 3, 2002, p. 324-328.
-
Zhang X. D., Zhu X. L., Bao Z. Grading learning for blind source separation. Science in China Series E, Vol. 32, Issue 5, 2002, p. 693-703.
-
Hyvarinen A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Transaction Neural Networks, Vol. 10, Issue 3, 1999, p. 626-634.
About this article
This work was financially supported by National Natural Science Foundation of China (Grant Nos. 51305142, 51305143), the General Financial Grant from the China Postdoctoral Science Foundation (Grant No. 2014M552429).
