Abstract
The severe ocean environment is obviously the source of many uncertain random loads on offshore structures. This harsh environment when acting on the slender top tensioned risers with high aspect ratio (L/D) causes multimodal vibration leading to fatigue failure. Thus, a reliable stress analysis procedure should be applied in the assessment of their long-term behaviors. This research is a study on the effect of boundary conditions on the total and local response of offshore risers due to loads in different sea states. A FEM code is developed for discretization of riser’s structural model and was run for the riser of Amirkabir semisubmersible vessel for 87 sea states in the Caspian Sea and four boundary conditions. The results show that the most severe stresses in the riser don’t happen essentially in the harshest environment. The comparison of boundary conditions shows that clamped-clamped boundaries lead to lowest stress values while the riser experiences a wider band of stress in the pinned-pinned boundary type. While the riser top end boundary condition highly influences the displacements and stresses even in the lower part of riser.
1. Introduction
Top-tensioned risers; the connecting line between offshore floating units and wellheads; are complex structures. They are exposed to a combination of stresses. The stress is associated with top tension and environmental loads bending moments. The aleatory nature of environmental loads from the waves, winds and currents, in addition to the epistemic nature of uncertainties caused by fluid induced vibrations and related loads, oblige the engineers to reduce the uncertainties toward a more reliable design.
Some researchers have studied the top tensioned risers. The most leading studies in this field can be categorized from different points of view. A crucial approach in classification of researches is the structural model of riser. A riser can be modeled as a tensioned rod [1] or a tensioned beam. The underlying assumption for modeling the riser as a beam is that the flexural rigidity of riser can’t be neglected [2-5]. Therefore, most researches have selected the Euler-Bernoulli beam theory for riser modeling [6, 7]. In this regard an essential part of structural modeling is selection of proper types of boundary conditions for governing equation of riser motion.
Top tensioned risers have complex and diverse kinds of connections. The connection to riser tensioner, wellhead global joint, heave compensator and other devices, besides the different working conditions exposes the riser to a wide variety of boundary conditions. Thus, for a long-term riser stress analysis, adequate accuracy should be considered for selection of boundary types.
Four different types of boundary conditions can be applied to riser structure. Most of researches applied pinned-pinned boundary conditions [3, 8]. But some have assumed clamped type [9, 10]. Other researches have also applied mixed types of boundary conditions and have considered the effect of vessel motion on the top end of riser [6].
To the best knowledge of authors, no published work has compared the effect of different types of joints on the riser. Although different types of boundary conditions have been considered in the previous researches, few physical interpretations for the assumptions were presented. In fact, risers experience different types of boundary conditions due to complexity of real joints. So, this paper focuses on the consequences of boundary type selection, in order to highlight its effect on the long-term behavior of risers.
To do this, at first the structural model and environmental loading is explained in Section 2. Then the long-term wave climate and selected sea states with a discussion on the analysis results are reported in Sections 3 and 4. The paper ends with the conclusion on pros and cons of each boundary type.
2. Riser analysis methodology
A top tension riser is a flexible pipe which connects the wellhead to offshore platform Fig. 1. It’s tensioned at top end on the vessel by means of a special apparatus called riser tensioner to prevent buckling under the effect of weight and to improve the stiffness. The analysis conducted in this research has been conducted on the data from the top tension riser of Amirkabir semisubmersible drilling platform which currently operates in the Caspian Sea. Analysis data is provided by Khazar Exploration and Production Company (KEPCO) and is listed in Table 1.
Fig. 1A schematic of riser in the marine environment
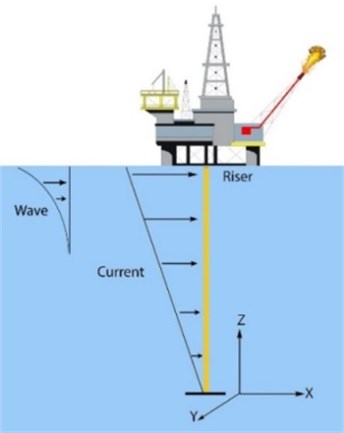
The origin of coordinates system is located on the center of riser in its contact point with the bottom wellhead as shown by Fig. 1. The transverse motion of a tensioned beam can be written as follows [5]:
where denotes the flexural rigidity, mass, the variable tension along the riser is defined by:
where is the submerged weight of riser defined as the difference between its dry weight and buoyancy. is the transverse force on the riser calculated via the following relation [6]:
In this equation is the marine current velocity along the riser:
and is the wave particle velocity, and are riser velocity and acceleration respectively while and denote the drag and added mass coefficients.
Table 1Riser properties
Property | Value |
Outer diameter () | 0.53 m |
Inner diameter () | 0.48 m |
Riser length | 800 m |
Modulus of elasticity | 2.07 GPa |
Water density | 1025 Kg/m3 |
Steel density | 7850 Kg/m3 |
Inner flow density | 998 Kg/m3 |
Added mass coefficient () | 2 |
Drag coefficient () | 0.7 |
Current velocity at surface () | 0.5 m/s |
Top tension () | 3000 KN |
Water depth () | 800 m |
Four types of boundary conditions for the riser were applied in this research. Both the top and bottom ends of riser can be constrained as pinned or clamped boundary types. So, there will be four possible combinations of boundary conditions. They are listed and described in Table 2.
A finite element based code was utilized for discretization of Eq. (1) and riser displacements were calculated. The stress in any point on riser can be obtained by the following relation:
where is the riser’s cross-sectional area.
Table 2Boundry types used in the analysis
Pinned-Pinned | Clamped-Pinned | Pinned-Clamped | Clamped-Clamped | |
Bottom Boundary Condition | ||||
Top Boundary Condition |
3. Long-term modeling of wave induced vibration of riser
To perform a long-term analysis of riser behavior, it’s assumed that the ocean environment in the lifetime of the structure can be characterized by a number of short-term sea states. The sea states and their probability of occurrences can be defined from direct measurements or hindcast methods [11]. Significant wave height () and peak spectral periods () are usually sorted in the form of wave scatter tables. Wave data used in this research was the data provided by Kepco. The table contains the probability of occurrence of 87 possible sea states. Fig. 2 shows these probabilities.
The riser’s equation of motion under the effect of wave and current has been solved in all the sea states. The results from four sea states are discussed in this paper. These sea states are listed in Table 3.
For each combination of and , the irregular wave is determined by a random irregular wave generated from a Pierson-Moskowitz spectrum. The spectrum is defined as [12]:
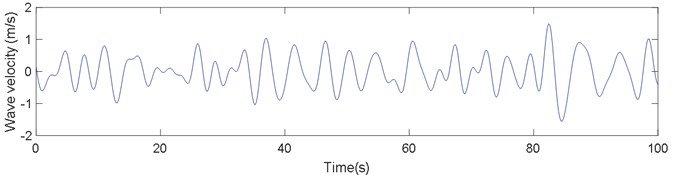
An example of time series of water particle velocities under wave in the sea state No. 41 is displayed in Fig. 3.
Table 3The representative sea states
Sea State ID | (m) | (s) |
41 | 1.75-2 | 5-6 |
66 | 3-3.25 | 8-9 |
86 | 4.75-5 | 9-10 |
87 | 5.25-5.5 | 9-10 |
Fig. 2Probability of occurence of combinations of Hs and Tp
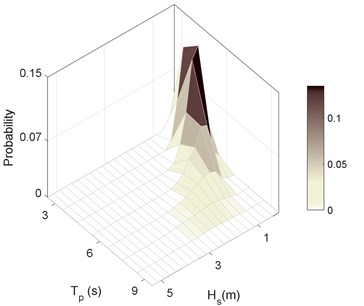
Fig. 3Surface wave velocity in No. 41 sea state
4. Results and discussion
As explained earlier, the finite element code [5] was solved for riser with four boundary conditions under the effect of 87 sea states. However before performing such a number of analysis, the code was verified with different tests. One of these tests is the comparison of natural frequencies with analytic relations. Among the prescribed boundary conditions the exact solution for natural frequency of a tensioned beam with constant tension over the length exists just for a beam with pinned-pinned boundary condition [13] and is defined by Rao as [14]:
Fig. 4 shows the accordance of natural frequencies from the present FEM code with the analytical solution of Eq. (7).
At the first stage of analyses, natural frequencies of the riser under four types of boundary conditions were calculated and are reported in Table 4.
Fig. 4Natural frequencies of risers
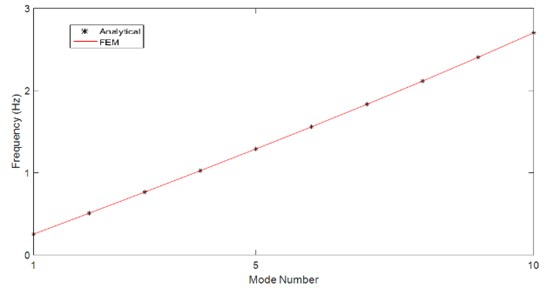
Table 4Natural frequencies of riser with four boundary conditions
Frequency (Hz) mode number | Pinned-Clamped | Clamped-Pinned | Clamped-Clamped | Pinned-Pinned |
1 | 0.1532 | 0.1607 | 0.1623 | 0.1518 |
2 | 0.3128 | 0.3265 | 0.3298 | 0.3098 |
3 | 0.4779 | 0.4966 | 0.5016 | 0.4733 |
4 | 0.6508 | 0.6730 | 0.6801 | 0.6442 |
5 | 0.8326 | 0.8574 | 0.8668 | 0.8239 |
A question may arise here from the difference between the results of C-P and P-C boundary types. Due to the variation of stiffness with the weight of riser, the natural frequencies of these two boundary types are different.
The second step is to check the validity of code. To do this, a comparison was made between the present code and data of Morooka, et al. [15]. The code shows good compatibility with their results. Fig. 5 is a comparison between the results of two works.
Fig. 5Comparison between the present model and Morooka et al. [15]
![Comparison between the present model and Morooka et al. [15]](https://static-01.extrica.com/articles/19110/19110-img5.jpg)
Comparisons were made to visualize the RMS of stress in different boundary conditions and different sea states. This analysis was a try to rapidly acquire the difference of riser behavior in different boundary conditions. The results were used for selection of some sea states for a more detailed study on the boundaries.
As can be deduced from Fig. 6, the riser experiences high stresses even in the mid-range sea states. The sea state No. 66 is thus selected as representative for these sea states. Selected Sea states were previously introduced in Table. 3. Another point that is inferable from Fig. 6 is the similarity between long-term stresses under the effect of different boundary conditions. The stress ranges in Figs. 6(b) and 6(d) (P-P and P-C boundary types) are more similar to each other and that is for Figs. 6(a) and 6(c) (C-C and C-P). This supports the idea that the effect of top boundary in general sounds to be much more than bottom boundary.
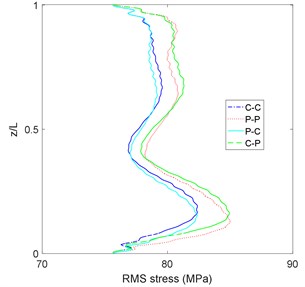
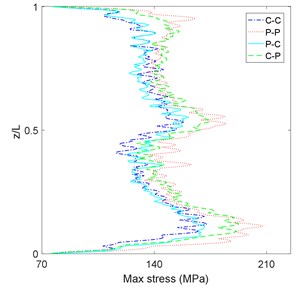
After defining the more critical sea states, the behavior of different location of riser should be checked. The RMS and maximum value of stress in the sea state No. 86 along the riser are displayed in Figs. 7(a) and 7(b).
Fig. 6RMS of riser stress in sea state No. 87 for different boundary types as: a) C-C, b) P-P, c) P-C, d) C-P. Stressess in (MPa)
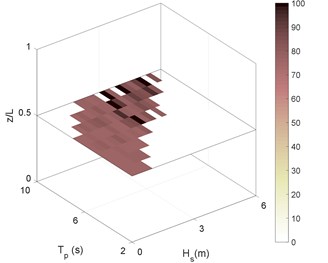
a)
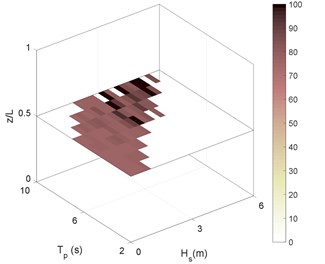
b)
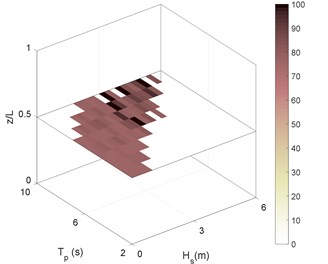
c)
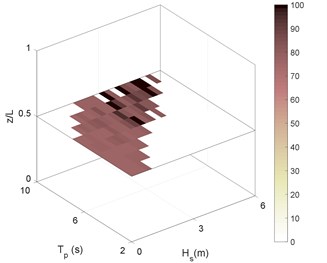
d)
Fig. 7Maximum and RMS of riser stress in sea state No. 86
a)
b)
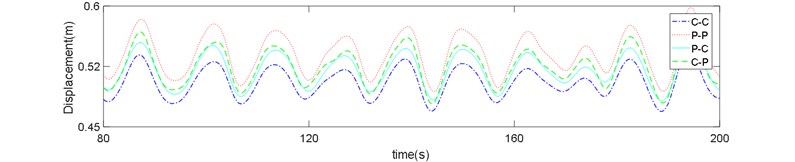
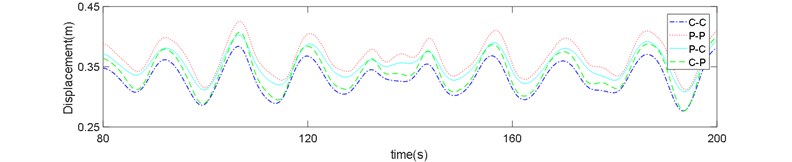
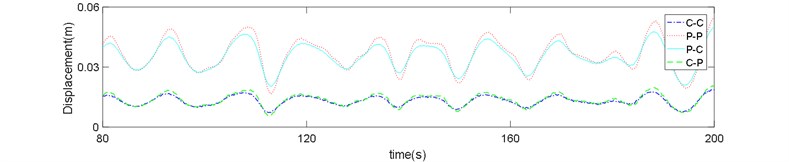
Fig. 8Risers response in sea state No. 66: a) z= 720 m, b) z= 400 m, c) z= 80 m
a)
b)
c)
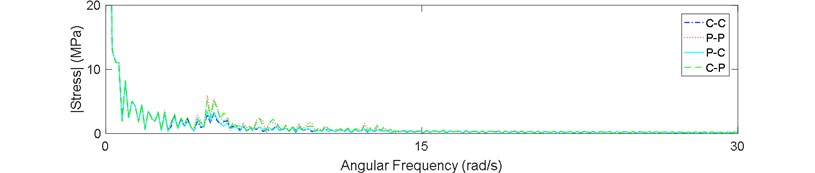
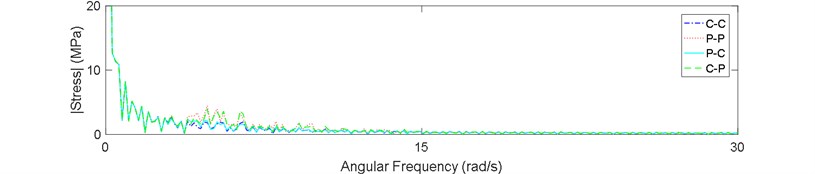
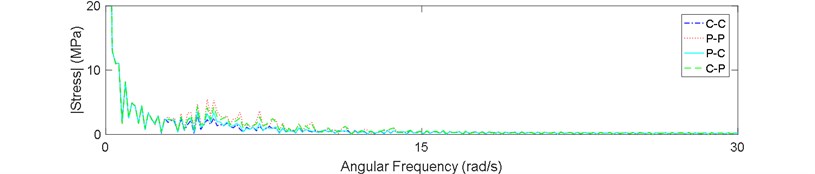
Fig. 9Stress spectrum of riser in sea state No. 87: a) z= 720 m, b) z= 400 m, c) z= 80 m
a)
b)
c)
The displacement time history of P-P boundary type shows higher displacements and variations compared to the other types.
Three points on the bottom, middle and upper section of riser were investigated and the time series of riser displacement in the sea state No. 66 is displayed in Figs. 8(a-c). It is clear from these figures that effect of boundary condition on the riser displacements is much greater in the bottom of riser. Although the mean difference between the displacement of C-C and C-P boundary types (both clamped in the bottom end) with the P-P and P-C types is nearly equal, but the value is noticeable compared with the absolute value of displacement at each point.
Finally, the stress spectrum was derived by a FFT for three points of riser in sea state No. 87. Figs. 9(a-c) show the results. It is clear in these figures that the spectrum has much more peaks in the P-P and C-P boundary types. The peaks are higher in the bottom part of the riser which means this part experiences a broader band of stresses.
Existence of these peaks in the spectrum of C-P and P-P boundary types shows that if the riser is assumed to be constrained with these boundary types, it probably experiences a more severe multi-modal type of vibration. It means that the effect of some modes dominates the whole structural response.
5. Conclusions
Top tensioned risers are critical elements of drilling and production offshore units. Due to different kinds of connections and operations they experience during their lifetime, they are opposed to various kinds of boundaries, many of which cannot simply be considered as typical kinds of boundary conditions. This research was a try to study the effect of boundary selection on the predicted stresses of risers in their lifetime.
The results also show that the riser top end boundary type plays an important role in the behavior of riser even in its lower part.
Finally, from comparison of RMS stress in different sea states, one can simply conclude that the highest levels of stress are not essentially inherent with more harsh sea states. Therefore, the riser behavior should also be carefully monitored during mid-range sea states.
References
-
Rustad A. M., Larsen C. M., Sørensen A. J. FEM modelling and automatic control for collision prevention of top tensioned risers. Marine Structures, Vol. 21, 2008, p. 80-112.
-
Khan R. A., Ahmad S. Bi-linear fatigue and fracture approach for safety analysis of an offshore structure. Journal of Offshore Mechanics and Arctic Engineering, Vol. 136, 2014, p. 1-7.
-
Low Y. M., Srinil N. VIV fatigue reliability analysis of marine risers with uncertainties in the wake oscillator model. Engineering Structures, Vol. 106, 2016, p. 96-108.
-
Xiaomin L. I., Haiyan G. U. O., Fanshun M. Fatigue life assessment of top tensioned risers under vortex-induced vibrations. Journal of Ocean University of China, Vol. 9, 2010, p. 43-47.
-
Huera Huarte F.-J. Multi-mode Vortex-Induced Vibrations of a Flexible Circular Cylinder. Ph.D. thesis, Imperial College London, 2006.
-
Xiaomin L. I., Haiyan G. U. O., Meng F. Stress analysis of top tensioned riser under random waves and vessel motions. Journal of Ocean University of China, Vol. 9, 2010, p. 251-256.
-
Xue H., Wang K., Tang W. A practical approach to predicting cross-flow and in-line VIV response for deepwater risers. Applied Ocean Research, Vol. 52, 2015, p. 92-101.
-
Chen W., Li M., Zhang L., Tan T. Study on multimode vortex-induced vibration of deepwater riser in different flow fields by finite element simulations. Journal of Offshore Mechanics and Arctic Engineering, Vol. 138, 2015, p. 1-9.
-
Murai M., Yamamoto M. An experimental analysis of the internal flow effects on marine risers. International Conference on Marine Technology, Dhaka, Bangladesh, 2010.
-
Skop R. A., Luo G. An inverse-direct method for predicting the vortex induced vibration of cylinders on uniform and nonuniform flows. Journal of Fluids and Structures, Vol. 15, 2000, p. 867-884.
-
Naess A., Moan T. Stochastic Dynamics of Marine Structures. Cambridge University Press, New York, 2013.
-
Patel M. H. Dynamics of Offshore Structures. Butterworth-Heinemann, 1989.
-
Bokaian A. Natural frequencies of beams under tensile axial loads. Journal of Sound and Vibration, Vol. 142, 1990, p. 481-498.
-
Rao S. S. Vibration of Continuous Systems. John Wiley and Sons, Hoboken, New Jersey, 2007.
-
Morooka C. K., Coelho F. M., Ribiero E. J. B., Ferrari J. A. J. Dynamic behavior of a vertical riser and service life reduction. 24th International Conference on Offshore Mechanics and Arctic Engineering, 2005.
About this article
The authors are grateful to Khazar Exploration and Production Company (Kepco) for the valuable riser structural and environmental data provided for this research.
