Abstract
Dynamic torsional vibration dampers are for a long time inherent integral components of internal combustion engines. One of the most common types of the dynamic dampers is a silicone damper. It has been, for many years, perceived as an exclusively viscous damper, thus it has been constructed and designed according to this perception. When compared to other types of dynamic dampers of the similar size with flexible components used for their construction, the standard viscous damper has a lower damping effect. Moreover, this damper type has been a significantly cheaper and simpler solution. Current silicone oils with high nominal viscosity, having not only the expected damping properties, but also significant elastic characteristics under alternate shear stress, enable construction of dynamic dampers with a higher damping effect than a viscous damper. Frequency and temperature dependent complicated rheological properties of high viscosity silicone fluids can only be identified experimentally using a suitable dynamic viscometer. However, the measured frequency dependencies of both components of the complex shear modulus are only defined for harmonic loading while internal combustion engine load is periodic and contains several tens harmonics. The key to the solution is therefore to find suitable multiparameter rheological models comprised of linear elastic and damping elements that would approximate in the specified frequency range both components of the complex shear modulus. Such a complicated task can be solved using efficient optimization algorithms. This article focuses on the mathematical description of convolute rheological properties of high viscosity silicone liquids and also contains an example of the application of created rheological models in the complex dynamic model of a V10 diesel engine. A computational tool for the determination of stiffness and damping coefficients of the multi-parameter rheological model was created and solved in the optimization software GAMS by means of the CONOPT solver. The possibility of these modern technologies is shown by the comparison of computation models and experimentally set torsional vibration spectres with standard viscous damper and damper utilizing a high viscosity silicone oil.
1. Introduction
Advancement in the automotive technology is characterized, in the long term, by power density increasing of internal combustion engines. The increase of the specific power and decrease of harmful emissions is gained by the application of supercharging and inclusion of new piston combustion engine concepts [1]. Simultaneously, the demands on their reliability and durability are increasing. When developing new types of internal combustion engines and when utilizing engines already mass-produced for different purposes, it is necessary to pay a considerable attention to the issues of complex dynamic analyses of engine powertrains and the devices connected to them. Predominantly, the issues of tuning, i.e. practically improved dynamic properties of these systems, are of constant and considerable importance. In the case of piston engine powertrains the tuning by changing the elements of the mass matrix and stiffness matrix of their mechanical structures is very difficult or impossible because of the construction, technology and economy context. In engineering practice so-called tuning subsystems, i.e. usually added dynamic systems with the number of degrees of freedom significantly smaller than the number of degrees of freedom of the base system are more often used. Their parameters can be set to the extent needed. Usually, simple systems of dynamic dampers are applied. These can be implemented by adding one mass element with viscoelastic coupling to the basic dynamic system. Characteristics of the individual types of dynamic dampers with one degree of freedom are presented in [2]. For their practical application, the crucial question is the extent to which the structural design enables the damper to achieve optimal parameters set out by their mathematical model.
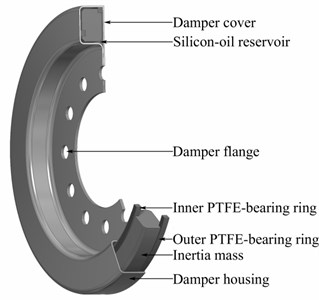
The most common type of dynamic torsional vibration damper of crankshafts is now a silicone damper which is used in engines of all sizes and specification; from engines for motor vehicles to the biggest stationary and ship engines. Previously used dampers that were structurally and technologically demanding, e.g. pendulum eliminators, were often replaced by the silicone dampers in these engines. A principal design of a silicone damper is shown in Fig. 1. The damper is formed by housing in which the ring is mounted with the centring rings. The space between the housing and the ring is filled with a viscous fluid, typically with a silicone oil. Possibilities of centring the ring in the housing, the way of filling the damper with silicone oil, and a number of other design and technological issues are the subject of a considerable number of patents.
Traditional calculation methods for the determination of the required viscosity of the liquid corresponding to optimal damping coefficient are based on the assumption that there is a laminar flow of viscous fluid between functional surfaces with a defined geometry [1, 2]. In the literature, the described methods of designing a viscous torsional vibration damper assume that the coupling of the damper ring and the housing is only a linear viscous element. Viscosity values determined in this way are then experimentally verified and eventually specified based on the measured torsional vibration spectra of a crankshaft with a viscous damper. In the early days of the application of viscous dampers to internal combustion engines, silicone fluids with relatively low viscosity values were available (from 0.02 m2s-1 to 0.06 m2s-1). Progress in the development of polymethylsilicone oils allowed for a gradual increase in the viscosity to values many times higher than the erstwhile values. In the measurement of torsional vibrations of engines using silicone dampers with oils of higher viscosities, it has been surprisingly found that the damping effect of the silicone dampers was greater than what corresponds to the so-called optimal damping [2]. The form of experimental results shows that it is possible to deduce the presence of a certain elastic element in the coupling of the ring and the damper housing. Considering the mechanical structure of silicone dampers, this may be only caused by properties of the liquid used, i.e. of silicone oils.
Fig. 1Design of a viscous type torsional vibration damper
2. Properties of silicone fluids under alternating shear stress
The main type of viscous liquid stress in a silicone damper according to Fig. 1 is the alternating shear. Standard procedures for the determination of properties of silicone fluids under alternating stress are not yet available. Literature data available indicate that there are laboratory researches for different purposes where the alternating stress was induced by various methods and in various frequency ranges which must be taken into account when using these results [3-11]. Under harmonic oscillating shear stress, the viscoelastic properties of the fluid may be described by a complex shear modulus:
Which defines the relation between the deformation angle and the shear stress as:
Or the complex viscosity:
Which shows the relation between the shear stress and the strain rate [12]. A comparison of definitions given in Eqs. (2) and (3) show the relationship between the complex shear modulus and complex viscosity components:
For applications in the field of silicone torsional vibration dampers, the usual frequency range is of several hundreds of Hz. Parameters of the elastic and damping coupling between the inertia ring and damper housing according to Fig. 1 are given by the shear stress integration on the corresponding inner surfaces of the damper. Based on the given geometry of the gaps between the inertia ring and the damper housing, a so-called “gap coefficient” may be determined. The complex stiffness of the coupling between the inertia ring and damper housing is then calculated as:
The real part of the complex stiffness given in Eq. (5) determines the storage of elastic energy, the imaginary part determines the viscous dissipation. Excitation forces and vibrations caused by them are predominantly periodic in the crankshaft mechanisms of internal combustion engines. In the dynamic computational models, several tens of harmonic components need to be taken into consideration to reach the necessary accuracy while solving in both frequency and time domains. Since the relations given in Eq. (1) and Eq. (5) are defined only for harmonic vibrations, they cannot directly be used for systems with periodic or general course of excitation forces. The solution could be a suitable multi-parameter linear viscoelastic model in which the frequency dependence of the real and imaginary part of the complex stiffness would, with necessary accuracy and within the given frequency range, approximate the courses based on Eq. (5) obtained from a measurement.
3. Rheological models and optimization of their structures and parameters
Rheological models are quite often used in automotive technology because they quite well approximate rheological properties and behaviour of a real material by a connection of simplest rheological elements – the spring and damper elements – in parallel or series order. The structure how the springs and dampers are connected and their values are dependent on a particular application. In this paper, high viscosity silicone oils used in viscous type torsional vibration dampers, initially studied in [13], are considered. Optimal spring and damper parameters were found by using an optimization model and with the use of measured complex shear modulus of silicone oils.
3.1. Measurement of the silicone oil complex shear modulus
The silicone oil with a high viscosity was considered for the investigation. The complex shear modulus was measured by a rotational dynamic viscometer for the frequency range between 10 Hz and 270 Hz with the step of 20 Hz. The measurements were carried out for four different temperatures of the oil. The simulations are shown for the temperature 110 °C which is the operating temperature of the silicone damper situated in the motor case of a V10 diesel engine.
3.2. Maxwell and general rheological models
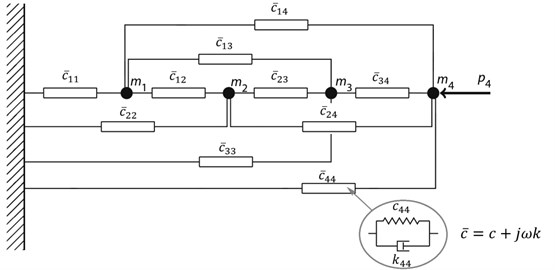
Two rheological models for the application with high viscosity silicone fluids were developed. One of the models is the fourth-order Maxwell model which can be understood as a frequently applied model in practice [2, 13], see Fig. 2. An element having the complex stiffness element represents a single serially-connected spring and damper elements and , respectively. All four elements with the complex stiffness are connected to the frame as well as to the mass point to which the force acts. The second model considered in the paper is the general model with no specific structure defined. The model consists of four mass points satisfying . Each mass point is connected to all the remaining mass points as well as to the frame by means of single Kelvin units, see Fig. 3. The number of elements in the general model is higher than in the case of the Maxwell model but the general model with all the elements is used only as a starting point for the optimization procedure - the optimization algorithm searches for a final structure of the general model having best results achieved with the lowest number of elements.
Fig. 2Fourth-order Maxwell model
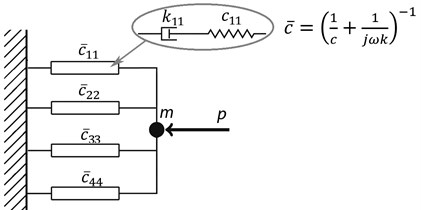
Fig. 3General rheological model with full structure
The complex stiffness of a single serial spring-damper element utilized in the Maxwell model can be calculated as [2]:
where is the damping coefficient, is the stiffness coefficient, is the imaginary unit and is the angular frequency. The complex stiffness of the Kelvin elements used in the general model can be described as [2]:
The real and imaginary parts of the complex stiffness () and (), respectively, are dependent on the frequency and as well as on the temperature. The complex stiffness of the system is then given as a solution of the linear set of equations:
where is the mass matrix, is the complex stiffness matrix, is the displacement vector and is the vector of forces. Finally, the complex stiffness is determined as:
where and are the last elements of the vectors and , respectively.
3.3. Parameter optimization of rheological models
An optimization model was developed with the aim to determine optimal values of rheological parameters (the stiffness and damping and , respectively) as well as an optimal structure of the general rheological model. The optimization approach is based on the mathematical programming method [14] applied to a nonlinear problem. The specialized optimization software called the General Algebraic Modelling System (GAMS) was used. The GAMS is a high-level modelling system for mathematical programming and optimization problems. It contains a number of integrated high-performance solvers for various types of optimization problems. In the problem investigated in the paper, the nonlinear solver CONOPT was applied [15]. Performed tests have proven significantly better results achieved with the use of GAMS than in case of heuristic methods [16, 17]. The CONOPT solver is based on the generalized reduced gradient (GRG) method [18, 19] applicable to nonlinear problems of mathematical programming with nonlinear constraints. The GRG method and its predecessor – the reduced gradient method – are algorithms based on the principle of feasible directions [20]. The objective function of the implemented optimization model was defined as:
With the constraints:
where and are the frequency-dependent real and imaginary parts of the complex stiffness, respectively, which were determined experimentally. and are the simulation values of the frequency-dependent real and imaginary part, respectively, calculated by the optimization model and is the number of samples in the frequency domain. Since the magnitudes of real and imaginary parts of the complex stiffness are of different orders, the relative error is incorporated in the objective function Eqs. (10). A closer look at the objective function reveals that the aim of the optimization is to find the values of the parameters and which minimize the sum of relative errors between the experimental and simulated data in the complete frequency range. From the view of the optimization model, the Maxwell model and the general model are virtually identical except of the fact that in the case of the Maxwell model some rheological parameters and are set to zero in order to form the predefined structure. The reason for such behaviour is that the Maxwell model is a special case of the general model.
The results gained from the optimization runs of the GAMS (in general, not only in case of the GAMS) are dependent on initial values of variables. Due to this reason, the optimization model was solved repeatedly 1000-times in a loop with the random generation of initial values. Then the best solution from the set of results from the loop was identified and considered as the final optimal solution.
3.4. Results of optimization procedure
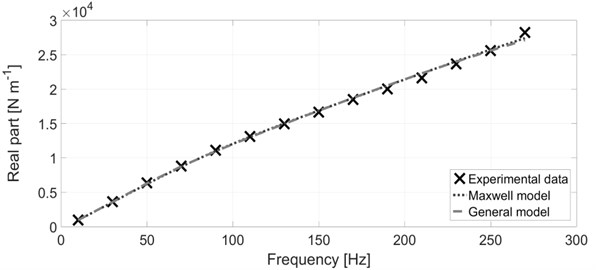
The silicone oil with a high viscosity was considered at the operating temperature of 110 °C which is the operating temperature of the silicone damper situated in the motor case of a V10 diesel engine. The frequency range between 10 Hz and 270 Hz with the step of 20 Hz is considered. Harmonic components of orders 7.5 and 5 are dominant in the V10 crank mechanism torsional spectrum. Since the nominal engine speed is 2200 min-1, the frequency range below 300 Hz shown in Fig. 4 and 5 is sufficient as an illustration. The results of the optimization procedure with the mass matrix 0 are presented in Figs. 4-7 and in Table 1. Fig. 4 shows the comparison between the experiment and simulation for the real part of the complex stiffness. As can be seen from the figure, the simulated results of the Maxwell model and of the general model are virtually identical and also in a very good agreement with the experimentally determined data. Fig. 5 presents the comparison for the imaginary part of the complex stiffness. Similarly, as in the case with the real part, both the Maxwell model and the general model are virtually identical and they greatly fit the experimental data.
Fig. 4The real part of the complex stiffness – comparison between experiment and simulation
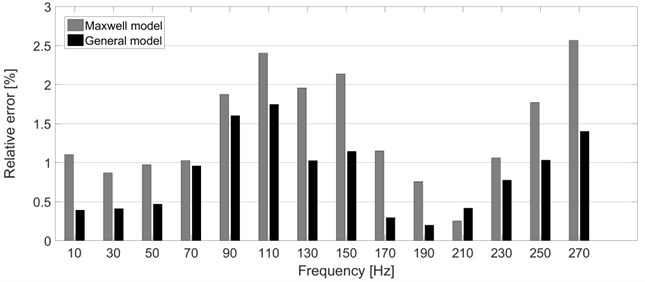
In order to investigate the results in more detail, the relative errors between the experimental and simulated data were investigated. The frequency-dependent relative error for the real and imaginary part of the complex stiffness are shown in Fig. 6-7. It can be seen from the figures that the relative error of results determined with the use of the general model is approximately a half of the relative error of results computed by the Maxwell model. As for the resultant objective function, the particular values denoted as OF are presented in Table 1 together with the particular values of the stiffness and damping coefficients and , respectively. The Maxwell model has eight parameters in total (four stiffness coefficients and four damping coefficients) from its nature. In case of the general model, the full model consists of 20 parameters in total (10 stiffness coefficients and 10 damping coefficients).
However, the best results were achieved with the structures consisting of eight parameters, i.e. the identical number as in case of the Maxwell model, see Fig. 8. It is worth pointing out that the objective function is considered as a quality indicator between the experiment and simulation; the lower the value of the objective function the better the approximation. As can be seen in Table 1. the general model allows for the approximation with about 20 % lower value of the objective function than in case of the Maxwell model. Since the general model is able to determine both the optimal structure and its parameters, these results make the general model easily applicable to a wide range of different materials used in various damping systems.
Fig. 5The imaginary part of the complex stiffness – comparison between experiment and simulation
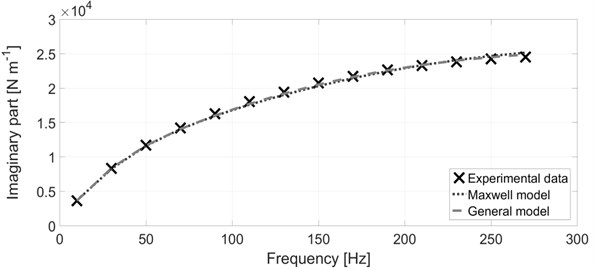
Fig. 6Relative error between the experimental and simulated data – real part of the complex stiffness
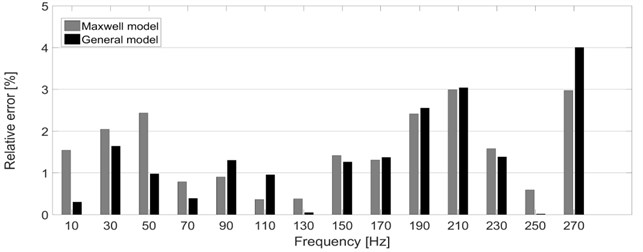
Fig. 7Relative error between the experimental and simulated data – imaginary part of the complex stiffness
4. Application of a high viscosity silicone damper
A viscous type of torsional vibration damper using silicone oil with a high nominal viscosity of 0.3 m2s-1 was applied to a V10 diesel engine which is used in heavy duty trucks. Fig. 9 shows the photo of the investigated V10 diesel engine and its crankshaft. The schematic of the crank mechanism of this engine with cylinder angle of 90 degrees is presented in Fig. 10. The finite element models of the main components of the crank mechanism, i.e. the crankshaft, the connecting rod, the piston group and others were subsequently converted into a multibody system. The crankshaft is mounted in rolling bearings with low frictional losses, their spring-damper computational models also respect the stiffness of the engine block in their locations. Computational models of the connecting rod sliding bearings are based on the Reynolds equation [2]. Measured indicator diagrams of the engine were used to calculate the excitation forces.
Fig. 8Optimized structure and its parameters for the general rheological model
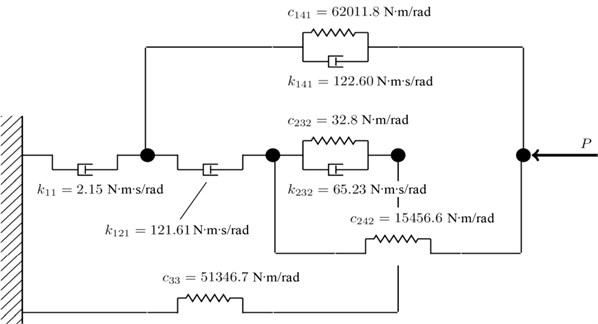
Table 1Optimized values of the stiffness and damping parameters
Parameter | Rheological model | |
General model | Maxwell model | |
[N·m·rad-1] | – | 3.91·104 |
[N·m·rad-1] | – | – |
[N·m·rad-1] | – | – |
[N·m·rad-1] | 6.20·104 | – |
[N·m·rad-1] | – | 1.49·1011 |
[N·m·rad-1] | 32.8052 | – |
[N·m·rad-1] | 1.55·104 | – |
[N·m·rad-1] | 5.13·104 | 1.37·103 |
[N·m·rad-1] | – | – |
[N·m·rad-1] | – | 9133.5 |
[N·m·s·rad-1] | 2.1514 | 20.21 |
[N·m·s·rad-1] | 121.6143 | – |
[N·m·s·rad-1] | – | – |
[N·m·s·rad-1] | 112.5965 | – |
[N·m·s·rad-1] | – | 2.11 |
[N·m·s·rad-1] | 65.2286 | – |
[N·m·s·rad-1] | – | – |
[N·m·s·rad-1] | – | 20.26 |
[N·m·s·rad-1] | – | – |
[N·m·s·rad-1] | – | 25.54 |
OF [N·m·rad-1] | 119.926 | 145.02 |
The damper ring according to Fig. 1 is centered to the housing using the PTFE-bearing rings. Therefore, it is enough to consider their mutual angular rotation in the 3D computational model of the crank mechanism. The coupling of the damper ring to housing is realized by the multi-parameter rheological model according to Fig. 8 in the 3D crank mechanism computational model. The individual linear elastic and damping elements according to Fig. 8 are modelled using 1D type elements, i.e. the torsion spring and the torsion damper from the element library of the multi-body system.
Fig. 9Investigated V10 diesel engine a) and its crankshaft b)

a)

b)
Fig. 10Schematic of the crank mechanism of the V10 diesel engine
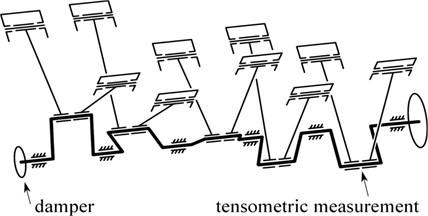
The results of this crank mechanism computational dynamic model show that substantial torsional vibrations with dominant harmonic orders 7.5 and 5 are formed in the crank mechanism. Fig. 11(a) shows the waveform of the maximum values that are evaluated from periodic signals of the torque at the crank pin by the flywheel. The results were subsequently verified by tensometric measurement as shown in Fig. 11. The strain gauges were affixed to the inside diameter of the hollow crankpin on the flywheel side. Inside the hollow crank web there was also installed a remote-controlled memory module for recording the measured data.
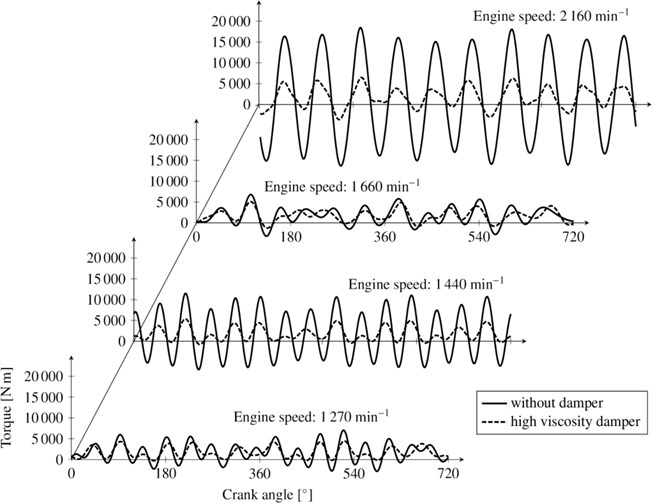
A viscous torsional vibration damper with the low viscosity of the silicone oil of 0.03 m2s-1 was proposed in the first step of the solution. The viscous damper optimal parameters were set according to the conventional procedure described in the literature [1, 2]. The results of the analysis of the computational model of the crank mechanism with this damper and the subsequent tensometry (see Fig. 11(b)) have shown that the torque reduction does not reach the level required. As a second step of the solution, the size of the torsional damper was doubled which was achieved by assembling two viscous dampers to the front end of the crankshaft. The computational model and the results of tensometric measurements show that the damping effect of the doubled damper is only slightly better than that of a single damper (see Fig. 11(c)) although the mass of the damper system has doubled. This negative result was assumed on the basis of knowledge followed from the optimal damping effect of a viscous damper in dependence to its relative size based on the analysis of a simple dynamic model [2]. As a more effective solution, a project of a viscous type damper using high viscosity silicone oil was then prepared. In the dynamic computational model of the V10 diesel engine crank mechanism, the general rheological model of the silicone oil according to Fig. 8 was used to create the coupling of the damper ring and housing, see Fig. 1. As variable parameters for the optimization algorithm, the moments of inertia of the damper ring and housing and the gap coefficient Λ according to Eq. (5) were set. The results of the computational model and the tensometric measurement are shown in Fig. 11(d). When compared with the traditional viscous damper of the same size (see Fig. 11(b)), the damping effect of the damper with the high viscosity silicone oil is significantly higher, which is also evident from the torque time behaviour in Fig. 12. This torsional vibration damper was subsequently applied in the production of the V10 diesel engine and based on the findings of long-term operation, it meets all requirements.
Fig. 11Maximum calculated and measured torque values at the crank pin by the flywheel
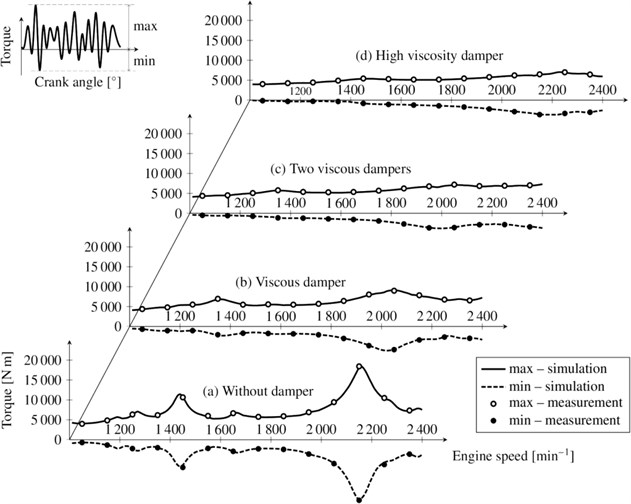
Fig. 12Periodical torques at the crank pin by the flywheel without damper and with high viscosity silicone damper
5. Conclusions
The approximation of the rheological properties of the silicone oil with the high viscosity was investigated with the use of the traditional fourth-order Maxwell model and with the use of the general rheological model. The Maxwell model with the fixed structure was allowed only for the determination of optimal stiffness and damping parameters while the general model was enabled to find an optimal structure and the corresponding optimal parameters. Although both the models provide a very good approximation, the results have shown that the general model allows for a better approximation and no special care is required to pre-design the structure of the model. These conclusions make the developed general model greatly applicable for various damping materials with various rheological properties. With the use of the rheological model of high viscosity silicone oil, the viscous type vibration damper for the V10 diesel engine was designed. The results of the complex dynamic computational model of its crank mechanism with one and two conventional viscous dampers and then with a damper using the high viscosity silicone oil were verified by tensometric torque measurement at the crank pin by the flywheel. High viscosity silicone oils enable to design unconventional torsional vibration dampers. Only their external view is similar to the known conventional viscous dampers but their damping effect is significantly greater.
References
-
Heisler H. Advanced Engine Technology. First Edition, Butterworth-Heinemann, Oxford, 1998.
-
Waller H., Schmidt R. Vibration theory for engineers: Theory, Simulation, Applications. First Edition, Wissenschaftsverlag, Zürich, 1989.
-
Barlow A. J., Harrison G. and Lamb J. Viscoelastic relaxation of polydimethylsiloxane liquids. Proceedings of the Royal Society of London, London: Royal Society, Vol. 1389, Issue 282, 1964, p. 228-251.
-
Iwamoto S. Experimental study on the effective viscosity of working oil for viscous torsional vibration damper. Journal of the Marine Engineering Society in Japan, 1974.
-
Ferry J. D. Viscoelastic Properties of Polymers. Wiley, New York, 1980.
-
Ghannam M. T., Esmail M. N. Rheological properties of poly (dimethylsiloxane). Industrial and Engineering Chemistry Research, Vol. 37, Issue 4, 1998, p. 1335-1340.
-
Tanner Roger I. Engineering Rheology. Oxford University Press, Oxford, 2000.
-
Sim H. G., Ahn K. H., Lee S. J. Large amplitude oscillatory shear behavior of complex fluids investigated by a network model: A guideline for classification. Journal of Non-Newtonian Fluid Mechanics, Vol. 112, Issue 2, 2003, p. 237-250.
-
Crassous J. J., Regisser R., Ballauff M., Willenbacher N. Characterization of the viscoelastic behaviour of complex fluids using the piezoelectric axial vibrator. Journal of Rheology, Vol. 49, Issue 4, 2005, p. 851-863.
-
Willenbacher N., Oelschlaeger C. Dynamics and structure of complex fluids from high frequency mechanical and optical rheometry. Current Opinion in Colloid and Interface Science, Vol. 12, Issue 1, 2007, p. 43-49.
-
Kokuti Z., Volker-Pop L., Brandstatter M., Kokavecz J., Ailer P., Palkovics L., Szabo G., Czirjak A. Exploring the nonlinear viscoelasticity of a high viscosity silicone oil with LAOS. Applied Rheology, Vol. 26, 2016, p. 14289.
-
Mezger T. G. The Rheology Handbook. Fourth Edition, Vincentz Network, Hannover, 2014.
-
Pistek V., Klimes L., Mauder T. Rheological models of high silicone fluids. Vibroengineering Procedia, Vol. 7, 2016, p. 25-30.
-
Bazaraa M. S., Sherali H. D., Shetty C. M. Nonlinear Programming: Theory and Algorithms. Third Edition, Wiley, 2006.
-
Drud A. Conopt – a GRG code for large sparse dynamic nonlinear optimization problems. Mathematical Programming, Vol. 31, Issue 2, 1985, p. 153-191.
-
Pistek V., Mauder T., Klimes L. Nonlinear optimization of generalized Kelvin-model parameters with the use of mathematical programming. Proceedings of International Conference Transport Means, 2014, p. 277-280.
-
Pistek V., Klimes L., Mauder T. Dynamic models of elastomer parts using mass-spring-damper system. Proceedings of International Conference Transport Means, 2015, p. 63-66.
-
Lasdon L.S., Fox R. L., Ratner M. W. Nonlinear optimization using generalized reduced gradient method. Revue Francaise D‘Automatique Informatique Recherche Operationnelle, Vol. 8, Issue NV3, 1974, p. 73-103.
-
Gabriele G. A., Ragsdell K. M. Large-scale non-linear programming using the generalized reduced gradient-method. Journal of Mechanical Design-Transactions of the ASME, Vol. 102, Issue 3, 1980, p. 566-573.
-
Bertsekas D. Nonlinear Programming. Third Edition, Athena Scientific, 2016.
About this article
This work is an output of the research project Netme Centre Plus (LO1202) by financial means from the Ministry of Education, Youth and Sports under the “National Sustainability Programme I”.
