Abstract
The paper is focused on the application of artificial neural networks (ANNs) in predicting the natural frequency of basalt fiber reinforced polymer (FRP) laminated, variable thickness plates. The author has found that the finite strip transition matrix (FSTM) approach is very effective to study the changes of plate natural frequencies due to intermediate elastic support (IES), but the method difficulty in terms of, a lot of calculations with large number of iterations is the main drawback of the method. For training and testing of the ANN model, a number of FSTM results for different classical boundary conditions (CBCs) with different values of elastic restraint coefficients () for IES have been carried out to training and testing an ANN model. The ANN model has been developed using multilayer perceptron (MLP) Feed-forward neural networks (FFNN). The adequacy of the developed model is verified by the regression coefficient () and Mean Square error (MSE) It was found that the R2 and MSE values are 0.986 and 0.0134 for train and 0.9966 and 0.0122 for test data respectively. The results showed that, the training algorithm of FFNN was sufficient enough in predicting the natural frequency in basalt FRP laminated, variable thickness plates with IES. To judge the ability and efficiency of the developed ANN model, MSE has been used. The results predicted by ANN are in very good agreement with the FSTM results. Consequently, the ANN is show to be effective in predicting the natural frequency of laminated composite plates.
1. Introduction
Continuous laminated plates and laminated composite plates with intermediate stiffeners are one of very common in composite structures that used in many engineering fields such as aerospace, civil and marine industries.
Natural frequencies of laminated composite structures are the classical tools for the intelligent diagnosis of composite defects (e.g. fiber breakage, matrix cracks, de-bonding and delamination). Vibration response has become an important tool in Structural health monitoring (SHM) in the last decades, the natural frequencies of composite structure are extracted and analyzed under each damage scenario as damage detection and localization technique based on the changes in vibration parameters. In the recent years, several approaches to find the natural frequencies and the mode shapes of laminated composite plates became a field that has attracted a lot of interest in the scientific community.
In order to find the natural frequencies and the mode shapes for different boundary conditions with IES, a numerical approach or an approximate method must be used. Several researchers are attracted to vibration of plates with IES. FSTM is one of a semi-analytical methods are welcomed in the many literatures as an alternative to the exact solution. In our previous paper by Altabey [1], a semi-analytical method, the FSTM approach has been used to investigate the free vibration of basalt FRP laminated variable thickness rectangular plates with IES. Since all of the coefficients in the FSTM method can be obtained, a lot of calculations with large number of iterations must be performed to obtain a frequency parameters, i.e. the time of solutions will be increased, and the large amount of data are required to study the changes of plate natural frequencies due to IES. This is the main drawback of the method identified so far.
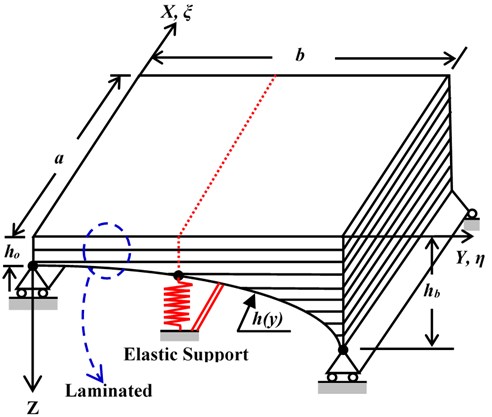
In the present study, the laminated composite plate shown in Fig. 1 has been modeled and analyzed using FSTM method. The laminated composite plate was manufactured using five symmetrically, angle-ply, laminates with the fiber orientations [45º/-45º/45º/-45º/45º] of basalt fiber and a polymer resin matrix. A predictive model for natural frequency in terms of fiber orientations is then developed using artificial neural networks. The developed model is tested with the FSTM data which were never used for developing the model. The FSTM results show that R2 and MSE are 0.986 and 0.0134 for train and 0.9966 and 0.0122 for test data respectively. Hence ANN model predicted results are in very good agreement with the FSTM results. Consequently, ANN are shown to be very effective in predicting the natural frequency of laminated composite plates under Four different CBCs are used in the analysis with different KT for IES.
Fig. 1The geometrical model of Basalt FRP laminated variable thickness rectangular plate with IES
2. Governing Equations
The normalized partial differential equation governing the vibration of symmetrically, angle-ply laminated, variable thickness, rectangular plates under the assumption of the classical deformation theory in terms of the plate deflection using the non-Dimensional variables and is given by [1, 2]:
where is the aspect ratio, also:
is the flexural rigidities matrix of the plate.
Since the treatment of IES conditions are the main objective of this paper we presented it in more details. At IES, , the displacement must vanish and the moment must be continuous, i.e. [1]:
3. Finite strip transition matrix (FSTM) with artificial neural network (ANN) method
3.1. Finite strip transition matrix (FSTM) method
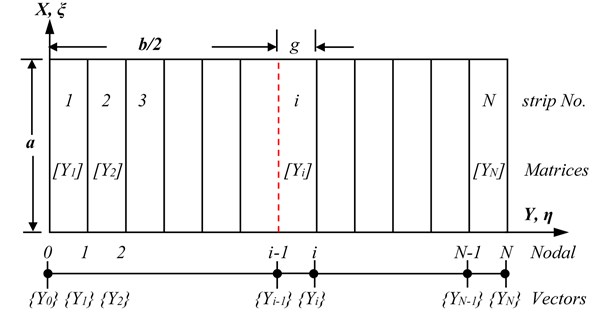
The method is made when such a shape function is not conveniently obtained in case of discussing the plate problems by series. The plate may be divided into N discrete longitudinal strips spanning between supports as shown in Fig. 2. By basic displacement interpolation functions may then be used to represent displacement field within and between individual strips.
For a plate striped in the -direction as shown in Fig. 2, the shape function may be assumed in the form:
where: is unknown function to be determined and is chosen a priori, the basic function in -direction.
Fig. 2Finite strip simulation on plate
3.2. Artificial neural network (ANN) modeling
Artificial neural network (ANN) is an attractive inductive approach for modeling non-linear and complex systems without explicit physical representation and thus provides an alternative approach for modeling hydrologic systems. Artificial neural network was first developed in the 1940s. Generally speaking, ANNs are information processing systems. In recent decades, considerable interest has been raised over their practical applications. Training of artificial neural network enables the system to capture the complex and non-linear relationships that are not easily analyzed by using conventional methods such as linear and multiple regression methods and the network is built directly from experimental or numerical data by its self-organizing capabilities. Based on the different applications, various types of neural network with various algorithms have been employed to solve the different problems. In this work will be using the preferred ANN structures to predict the frequency parameter of presented numerical conditions.
3.2.1. ANN configuration
Since the ANN configuration has a great influence on the predictive quality, various arrangements have been considered in previous work. It is necessary to define a simple code to describe the ANN configuration, as follows:
where and are the element numbers of input and output parameters, respectively, and is the number of hidden layers. and are numbers of neurons in each hidden layer, respectively. For example, means a one hidden layer ANN with seven input and one output parameters, with the hidden layer containing 21 elements (neurons); denotes a nine input and one output ANN, with 15 and 10 neurons, respectively, in two hidden layers.
The powerful function of an ANN is due to the neurons within the hidden layers, as well as to the related interconnections. Networks are also sensitive to the number of neurons in their hidden layers. It is believed that an ANN can represent any reasonable relationship between input and output if the hidden layers have enough neurons. However, for the practical case, more hidden neurons bring more interconnections, which require, in turn, larger training datasets for learning the relationships. It is therefore always necessary to optimize the number of neurons of the ANN hidden layers, as demonstrated by Demuth and Beale [3].
3.2.2. Performance evaluation measures
It is very useful from the designer point of view to have a neural system aids to decide whether his suggested design is suitable or not by Compute the MSE from equation:
where: is the predicted frequency parameter from ANN, is the target or computed values from FSTM method of frequency parameter, and is the number of FSTM computed data values.
Thus, the performance index will either have one global minimum, depending on the characteristics of the input vectors. Local minimum is the minimum of a function over a limited range of input values. Local minimum is an unavoidable when the ANN is fitted. So, a local minimum may be good or bad depending on how close the local minimum is to the global minimum and how low an MSE is required. In any case, the method applied to solve this problem and descent the local minimum with momentum. Momentum allows a network to respond not only to the local gradient, but also to recent trends in the error surface. Without momentum a network may get stuck in a shallow local minimum.
The estimation performances of frequency parameter is evaluated by the lack of fit with the regression coefficient of the multiple determination ; is defined as:
The value of is equal to or lower than 1.0. A higher value of implies a better fit. When the ANN shows a very good fit, approaches 1.0. A good fit of the ANN means that the ANN gives good estimations for the dielectric properties change used for the regression. Lower values means poorer estimations and the error band of the estimated result is wider.
3.3. Feed-forward neural networks (FFNN)
In this work we will use the suggested feed forward neural network, FFNN, to predict natural frequency of basalt FRP composite plate, because it has minimum mean square error (MSE), in composite structure applications [4, 5]. FFNN in general consist of a layer of input neurons, a layer of output neurons and one or more layers of hidden neurons [6]. Neurons in each layer are interconnected fully to previous and next layer neurons with each interconnection have associated connection strength or weight. The activation function used in the hidden and output layers neurons is nonlinear, where as for the input layer no activation function is used since no computation is involved in that layer. Information flows from one layer to the other layer in a feed-forward manner. Various functions are used to model the neuron activity such as liner transfer function (), Tan-Sigmoid transfer function () or Radial Basis (Gaussian) transfer functions ().
The training process is terminated either when the (MSE) between the observed data and the ANN outcomes for all elements in the training set has reached a pre-specified threshold or after the completion of a pre-specified number of learning epochs.
4. Results and discussion
In this work, The FSTM with ANNs techniques are used to predict the free vibration of the laminated composite plate shown in Fig. 1. The plate was manufactured using five symmetrically, angle-ply, laminates with the fiber orientations [////] is [45°/–45°/45°/–45°/45°] of basalt fiber and a polymer resin matrix. Physical and mechanical properties of the basalt FRP laminate composite plate are shown in Table 1.
Table 1Physical and mechanical properties of the basalt FRP
96.74 GPa | 22.55 GPa | 10.64 GPa | 8.73GPa | 0.3 | 0.6 | 2700 kg/m3 |
The non-dimensional frequency parameter are addressed in form [1]:
The plate has linear deformation in thickness woth non-dimensional form [1]:
where: is the tapered ratio of plate given by , () is the thickness of the plate at 0 and () is the thickness of the plate at 1.
4.1. Convergence study and accuracy
In this subsection, the author has carried out for convergening the proposed method, first six frequencies are calculated and compared with available results in literatures [1]. He compared the computational results of FSTM method from previous work [1] with values available from literatures [7, 8] for E-glass/ epoxy, square (1.0), uniform thickness (0) plates with elastic foundation support, the mechanical properties of the plate material are 0.23, , and . Two different CBCs (SSSS and CCCC) are used in calculations, KT is taken equal to 500, 1390.2 for SSSS and CCCC respectively. In this study are addressed in form . He found the results by FSTM method are in a very close agreement with results in References [7, 8] and the convergence speed can be achieved with terms of series solution ( 3 to 7).
4.2. Finite strip transition matrix (FSTM) results
In the present study, the numerical computations using FSTM approach is applied with an ANNs, which are combined to decrease detection effort to discern for different KT by minimizing the number of FSTM computations in order to keep save the time of calculations to a minimum. The method has successfully computations of the frequency parameter using only two different , the first one is located at 50 the second is 750, respectively, as shown in Table 2.
Table 2 presents the first six frequencies of the laminated composite plate shown in Fig. 1. The plate has the parameters of aspect ratio () and thickness tapered ratio () are 0.5. The Four different type of CBCs (SSSS, CCCC, SSFF and CCFF) and two different values of KT of IES are used in the calculations to study the changes of natural frequencies due to IES. The locations of the IES is at mid-line of the presented plate.
Table 2The first six frequencies of laminated, plate shown in Fig. 1 for two different values of KT, (Δ=0.5), (β=0.5)
SSSS | 50 | 22.1450 | 36.2210 | 53.5870 | 78.2360 | 105.5870 | 138.6970 |
750 | 55.0692 | 69.1452 | 86.5112 | 111.1602 | 138.5112 | 171.6212 | |
CCCC | 50 | 28.4310 | 46.5025 | 68.7979 | 100.4437 | 135.5584 | 178.0668 |
750 | 61.3551 | 79.4267 | 101.7221 | 133.3678 | 168.4826 | 210.9910 | |
SSFF | 50 | 12.2750 | 20.0773 | 29.7033 | 43.3663 | 58.5270 | 76.8799 |
750 | 45.1992 | 53.0015 | 62.6275 | 76.2905 | 91.4511 | 109.8041 | |
CCFF | 50 | 19.5928 | 32.0466 | 47.4112 | 69.2194 | 93.4182 | 122.7123 |
750 | 52.5170 | 64.9707 | 80.3353 | 102.1436 | 126.3424 | 155.6365 |
4.3. A feed-forward neural network (FFNN) design for predicting frequency parameters
A FFNN configuration in this case was , with tan-sigmoid neurons for the first layer while the second layer has pure linear ones. FFNN is trained by measuring values of , to predict for four different CBCs are SSSS, CCCC, SSFF and CCFF. Determination of the hidden layer, in addition to the number of nodes in the input and output layers, for providing the best training results, was the initial phase of the training procedure. The target for MSE to be reached at the end of the simulations was 0.001. Since the second step was largely a trial-and-error process, and involved FFNNs with the number of hidden layer neurons more than five, it did not show any sizeable improvement in prediction accuracy. Thus, the number of neurons for the single hidden layer was selected as five neurons. Selection of the number of hidden layer neurons, with respect to the MSE term is shown in Fig. 3. In the first FFNN structure is applied for training the results data of FSTM. Fig. 4 shows the training performance of suggested FFNN.
Fig. 5 represents the comparison between the FSTM data and the feed-forward neural network FFNN predicted data () for 50 of four different CBCs are SSSS, CCCC, SSFF and CCFF. The results of this NN show much satisfactory predication quality for this case study. Fig. 6 shows the comparison between the FSTM data and the feed forward neural network FFNN expected (tested) data for 750 of four different CBCs are SSSS, CCCC, SSFF and CCFF. From Fig. 6, it noted that the expected data from the suggested FFNN are applicable with the FSTM data.
Fig. 3Plot of MSE terms corresponding to the number of hidden layer neurons, used for selecting the optimum number of hidden layer neurons
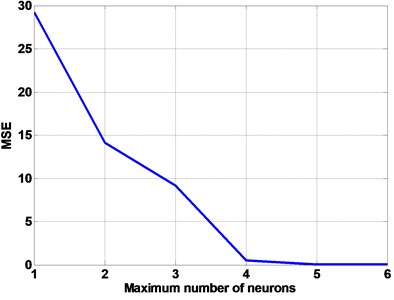
Fig. 4Training performance of suggested FFNN
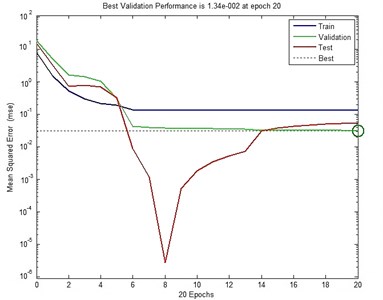
Fig. 5Comparison between the FSTM data and FFNN predicted data for Ω
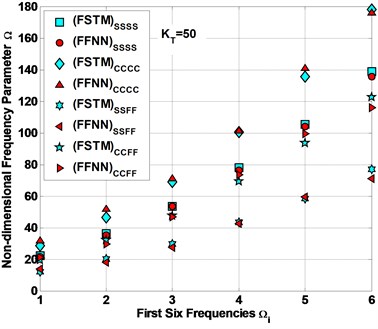
Fig. 6Comparison between the FSTM data and FFNN expected data for Ω
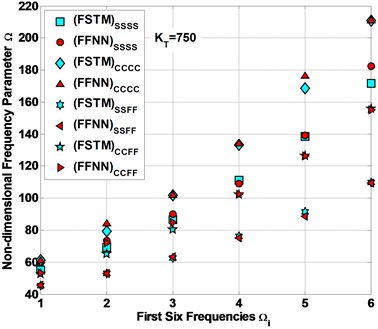
Fig. 7The performances of the present FFNN to predict data of Ω
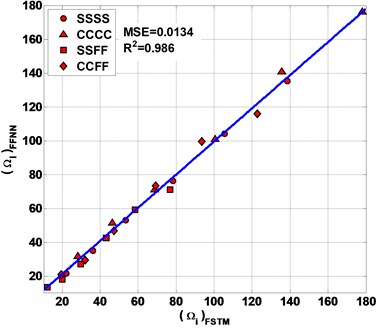
Fig. 8The performances of the present FFNN to expect data of Ω
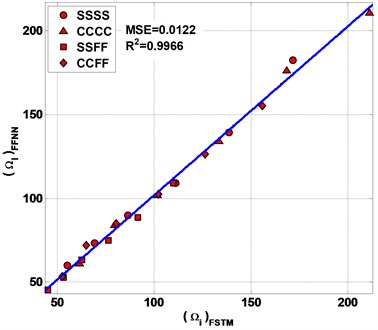
Table 3Mean square error (MSE) and regression coefficient (R2) values
Data | MSE | |
Predicted | 0.0134 | 0.986 |
Expected | 0.0122 | 0.9966 |
Table 3 and Figs. 7 and 8 represent the performances of the present FFNN by calculating the values of MSE and (see Eqs. (5, 6)) between FSTM data for both FFNN predicted and expected data for . As shown in Fig. 7 the value of MSE and between the FSTM and FFNN predicted data are 0.0134 and 0.986 respectively. From Fig. 8 the value of MSE and between the FSTM and FFNN expected data are 0.0122 and 0.9966 respectively.
4.4. The use of present FFNN for predicting non-FSTM data of non-dimensional frequency parameter
The main goal of the artificial neural network design is predicting non- FSTM data. In this section we will use the suggested FFNN to predict some non- FSTM data not included in FSTM evaluation. It is selected to use seven different , for four types of CBCs (SSSS, CCCC, SSFF and CCFF). The previous parameters , are the input vectors for artificial neural network, while the output is the signal vector is .
Fig. 9The FFNN predicted non-FSTM results of non-dimensional frequency parameter Ω
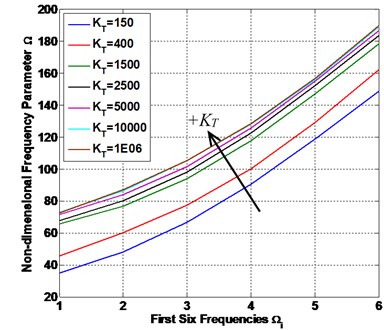
a) SSSS
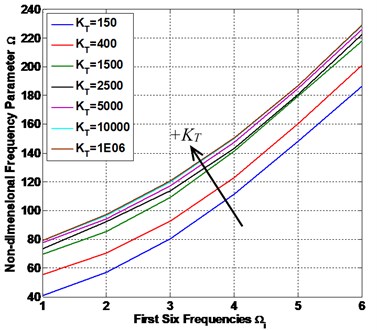
b) CCCC
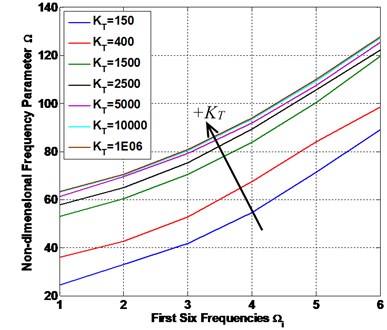
c) SSFF
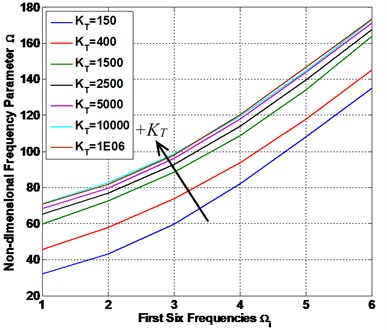
d) CCFF
Table 4The predicted non-FSTM results of the first six frequencies by FFNN
SSSS | 150 | Ref [1] | 34.6580 | 48.7340 | 66.1000 | 90.7490 | 118.1000 | 151.2100 |
FFNN | 34.8971 | 48.1343 | 66.6159 | 90.5891 | 118.8782 | 148.7286 | ||
400 | Ref [1] | 45.8453 | 59.9213 | 77.2873 | 101.9363 | 129.2873 | 162.3973 | |
FFNN | 45.8453 | 60.1268 | 77.2873 | 100.2624 | 129.2873 | 162.3973 | ||
1500 | Ref [1] | 62.4709 | 76.5469 | 93.9129 | 118.5619 | 145.9129 | 179.0229 | |
FFNN | 65.5428 | 76.7674 | 93.799 | 117.6289 | 147.1225 | 178.4941 | ||
2500 | Ref [1] | 67.5270 | 81.6030 | 98.9690 | 123.6180 | 150.9690 | 184.0790 | |
FFNN | 67.6715 | 80.0752 | 98.248 | 122.7383 | 152.2729 | 183.4709 | ||
5000 | Ref [1] | 70.7832 | 84.8592 | 102.2252 | 126.8742 | 154.2252 | 187.3352 | |
FFNN | 71.5277 | 83.8535 | 101.5647 | 125.5413 | 154.9449 | 186.8396 | ||
10000 | Ref [1] | 72.7065 | 86.7825 | 104.1485 | 128.7975 | 156.1485 | 189.2585 | |
FFNN | 72.8107 | 86.2942 | 105.2392 | 128.2564 | 156.1388 | 189.2703 | ||
1E+06 | Ref [1] | 73.1195 | 87.1955 | 104.5615 | 129.2105 | 156.5615 | 189.6715 | |
FFNN | 72.6947 | 87.0396 | 105.4209 | 128.5854 | 156.8348 | 189.6596 | ||
CCCC | 150 | Ref [1] | 40.9440 | 59.0155 | 81.3109 | 112.9567 | 148.0714 | 190.5798 |
FFNN | 41.0549 | 57.0992 | 80.3422 | 111.2997 | 148.2179 | 186.4952 | ||
400 | Ref [1] | 52.1313 | 70.2028 | 92.4983 | 124.1440 | 159.2587 | 201.7672 | |
FFNN | 55.4754 | 70.442 | 92.6468 | 123.0928 | 160.6131 | 201.1848 | ||
1500 | Ref [1] | 68.7569 | 86.8284 | 109.1239 | 140.7696 | 175.8843 | 218.3928 | |
FFNN | 69.7659 | 85.3865 | 109.1148 | 141.4497 | 179.6854 | 218.0006 | ||
2500 | Ref [1] | 73.8130 | 91.8845 | 114.1800 | 145.8257 | 180.9404 | 223.4489 | |
FFNN | 73.4808 | 92.2119 | 113.7449 | 143.3314 | 180.9021 | 222.5692 | ||
5000 | Ref [1] | 77.0692 | 95.1407 | 117.4361 | 149.0819 | 184.1966 | 226.7050 | |
FFNN | 77.8273 | 94.092 | 117.0825 | 147.6263 | 184.9599 | 226.1968 | ||
10000 | Ref [1] | 78.9925 | 97.0640 | 119.3594 | 151.0052 | 186.1199 | 228.6283 | |
FFNN | 79.3118 | 96.3864 | 119.7441 | 150.1071 | 187.0576 | 228.5796 | ||
1E+06 | Ref [1] | 79.4055 | 97.4770 | 119.7724 | 151.4182 | 186.5329 | 229.0413 | |
FFNN | 79.1422 | 97.2499 | 120.7791 | 150.5119 | 186.7872 | 229.1948 | ||
SSFF | 150 | Ref [1] | 24.7880 | 32.5903 | 42.2163 | 55.8793 | 71.0400 | 89.3929 |
FFNN | 24.4094 | 32.9047 | 41.7941 | 54.6268 | 71.2814 | 89.0171 | ||
400 | Ref [1] | 35.9753 | 43.7777 | 53.4036 | 67.0666 | 82.2273 | 100.5802 | |
FFNN | 35.9713 | 42.5469 | 52.8278 | 67.4484 | 83.9108 | 98.563 | ||
1500 | Ref [1] | 52.6009 | 60.4033 | 70.0293 | 83.6922 | 98.8529 | 117.2058 | |
FFNN | 52.904 | 60.2689 | 70.3874 | 83.7121 | 100.3213 | 119.6639 | ||
2500 | Ref [1] | 57.6570 | 65.4594 | 75.0853 | 88.7483 | 103.9090 | 122.2619 | |
FFNN | 57.9028 | 64.964 | 75.361 | 89.2589 | 105.6161 | 122.2164 | ||
5000 | Ref [1] | 60.9132 | 68.7155 | 78.3415 | 92.0045 | 107.1652 | 125.5181 | |
FFNN | 61.3157 | 69.5938 | 79.1805 | 91.7539 | 107.5848 | 125.4066 | ||
10000 | Ref [1] | 62.8365 | 70.6388 | 80.2648 | 93.9278 | 109.0885 | 127.4414 | |
FFNN | 63.0778 | 70.2994 | 80.2805 | 93.3565 | 109.3353 | 127.2809 | ||
1E+06 | Ref [1] | 63.2495 | 71.0518 | 80.6778 | 94.3408 | 109.5015 | 127.8544 | |
FFNN | 63.3054 | 70.5596 | 80.69 | 93.9744 | 110.0274 | 127.6158 | ||
CCFF | 150 | Ref [1] | 32.1058 | 44.5596 | 59.9242 | 81.7324 | 105.9312 | 135.2253 |
FFNN | 32.1827 | 43.2269 | 59.686 | 81.9174 | 108.2676 | 135.0946 | ||
400 | Ref [1] | 43.2931 | 55.7469 | 71.1115 | 92.9197 | 117.1185 | 146.4127 | |
FFNN | 45.562 | 57.8813 | 73.8431 | 93.8403 | 117.8631 | 145.3086 | ||
1500 | Ref [1] | 59.9187 | 72.3725 | 87.7371 | 109.5453 | 133.7442 | 163.0383 | |
FFNN | 59.6275 | 72.4773 | 88.4423 | 108.7844 | 134.0482 | 163.8665 | ||
2500 | Ref [1] | 64.9748 | 77.4286 | 92.7932 | 114.6014 | 138.8002 | 168.0944 | |
FFNN | 65.0645 | 76.7108 | 92.8809 | 114.0148 | 139.5554 | 167.6554 | ||
5000 | Ref [1] | 68.2310 | 80.6848 | 96.0494 | 117.8576 | 142.0564 | 171.3505 | |
FFNN | 68.3337 | 79.7057 | 96.0889 | 117.8545 | 143.8554 | 171.2413 | ||
10000 | Ref [1] | 70.1543 | 82.6081 | 97.9727 | 119.7809 | 143.9797 | 173.2738 | |
FFNN | 70.9017 | 82.7021 | 98.6556 | 119.3321 | 144.5419 | 173.0477 | ||
1E+06 | Ref [1] | 70.5673 | 83.0211 | 98.3857 | 120.1939 | 144.3927 | 173.6868 | |
FFNN | 70.6424 | 81.6968 | 98.1541 | 120.3744 | 146.7246 | 173.5624 |
Fig. 10The performances of the present FFNN to predicted non-FSTM results of non-dimensional frequency parameter Ω
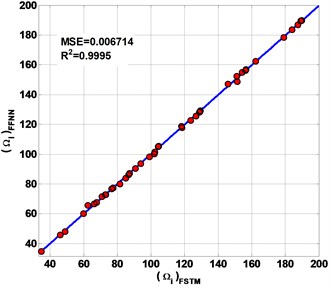
a) SSSS
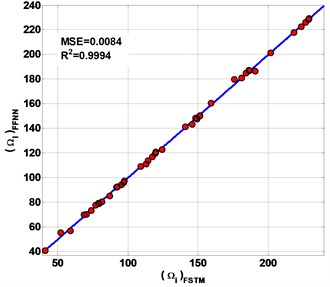
b) CCCC
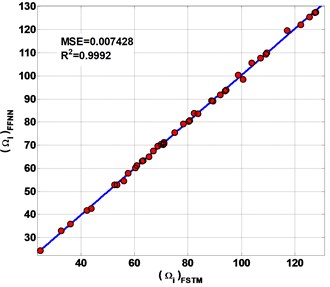
c) SSFF
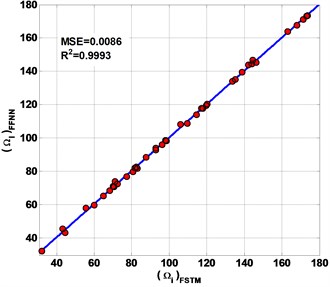
d) CCFF
Fig. 9 shows the FFNN predicted results of the first six frequencies of the laminated composite plate are presented in this study. The plate has 0.5 and 0.5 with four different types of CBCs.
The predicted non-FSTM results of the first six frequencies by FFNN and a comparison with the previous work results in literature of FSTM method by Altabey [1] are presented in Table 4. As a result, a FFNN gave good prediction for non-FSTM data even for extrapolations in presented laminated composite plate.
From Table 4 and Fig. 9, we can see, the first six frequencies increase with the increasing of the value of and we are observed that the gap between values of frequencies in the small and next values of are higher than the gap between values of frequencies in the large , and the frequencies at high values of are almost constant, for all conditions (SSSS, CCCC, SSFF and CCFF). On the other hand, the fully clamped (CCCC) and semi-simply supported (SSFF) condition have the higher and lower values of frequencies respectively and the other two conditions (SSSS) and (CCFF) are lie between them with an intermediate value. This conclusion was found in other work [1].
of non-FSTM results are 0.9995, 0.9994, 0.9992 and 0.9993 for SSSS, CCCC, SSFF and CCFF plate respectively. All of the predicting results are plotted on the diagonal line (Fig. 10) to observe the performances of the present FFNN to predict non-FSTM of . The MSE is defined of the predicted non- FSTM. The MSE is of non-FSTM results are 0.006714, 0.0084, 0.007428 and 0.0086 for SSSS, CCCC, SSFF and CCFF plate respectively.
5. Conclusions
The natural frequency values were found by analyses which were done of basalt FRP laminated variable thickness rectangular plates with IES by FSTM method and ANNs algorithm, which are combined to decrease computational effort to discern natural frequency in basalt FRP laminated composite plates, in order to save the time of the FSTM computational data to a minimum with high accuracy and easy. Based on the FSTM results and the results predicted by artificial neural networks, the following conclusions are drawn for laminated composite material plates.
1) The FFNN model has been developed by considering the and ply angle () as the input for predicting . The developed FFNN model could predict with the and MSE are 0.986 and 0.0134 for training data set and 0.9966 and 0.0122 for test data respectively.
2) The FFNN model could predict non-FSTM of with of non-FSTM results are 0.9995, 0.9994, 0.9992 and 0.9993 for SSSS, CCCC, SSFF and CCFF plate respectively. The MSE is defined of the predicted non-FSTM. The MSE is of non-FSTM results are 0.006714, 0.0084, 0.007428 and 0.0086 for SSSS, CCCC, SSFF and CCFF plate respectively.
3) The ANN predicted results are in very good agreement with the FSTM results.
References
-
Altabey W. A. Free vibration of basalt FRP laminated variable thickness plates with intermediate elastic support using finite strip transition matrix (FSTM) method. Journal of Vibroengineering, Vol. 19, Issue 4, 2017, (in Press).
-
Chakraverty S. Vibration of Plates. CRC Press, Taylor and Francis Group, 2009.
-
Demuth H., Beale M. Neural Network Toolbox User’s Guide for use with MATLAB Version 4.0. The Math Works, Inc., 2000.
-
Al-Tabey W. A. The Fatigue Behavior of Woven-Roving Glass Fiber Reinforced Epoxy under Combined Bending Moment and Hydrostatic Pressure. Ph.D. Theses, Alexandria University, Egypt, 2015.
-
Altabey W. A. Fatigue life prediction for carbon fiber/epoxy laminate composites under spectrum loading using two different neural network architectures. International Journal of Sustainable Materials and Structural Systems, 2017, (in Press).
-
Skapura D. Building Neural Networks. ACM Press, Addison-Wesley Publishing Company, New York, 1996.
-
Zhou D., Cheung Y. K., Lo S. H., Au F. T. K. Three dimensional vibration analysis of rectangular thick plates on Pasternak foundation. International Journal of Numerical Methods in Engineering, Vol. 59, 2004, p. 1313-1334.
-
Ferreira J. M., Roque C. M. C., Neves A. M. A., Jorge R. M. N., Soares C. M. M. Analysis of plates on Pasternak foundations by radial basis functions. Journal of Computational Mechanics, Vol. 46, 2010, p. 791-803.
