Abstract
In this paper, comparison between G-N model of type II (without energy dissipation) and G-N model of type III (with energy dissipation) has been shown in a three dimensional thermoelastic half space with rotation subjected to time dependent heat source on the traction free boundary. Eigenvalue methodology has been adopted to solve the equations resulting from the application of the Normal mode analysis to the non-dimensional coupled equations. Variation of the numerically computed values of thermal stresses and temperature with and without rotation has been illustrated graphically.
1. Introduction
The inconsistency of heat conduction equation of classical uncoupled theory of thermoelasticity with the experimental results is due to the fact that i. no elastic term is included to account for elastic changes producing heat effects; ii. parabolic nature of heat conduction equation indicating infinite speed of propagation of heat waves means that thermal disturbances (with infinite speed) and elastic disturbances (with finite speed) from the classical theory of thermoelasticity, are coupled together. This suggests that every solution of the equations has a part which extends to infinity.
Biot [1] developed a theory of irreversible thermodynamics and gave a satisfactory derivation of the linear theory of coupled thermoelasticity. In order to obtain a wave type heat conduction equation the concept of generalized thermoelasticity was introduced modifying CCTE and later extended by Dhaliwal and Sherief [3] for anisotropic body, and the uniqueness of the solutions was proved by Ignaczak [2, 4]. Green-Naghdi proposed a generalized thermoelasticity by modifying the energy equation. There are three types of constitutive relations in G-N model [6-8]. Type-I leads to classical heat conduction equation. Type-II provides solutions for thermal waves propagating finite speed without energy dissipation (TEWOED) and type-III also confirms propagation of thermal waves of finite speed with energy dissipation (TEWED). Several investigations with these extensions have been studied by Abd-Alla and Abo-Dahab [11], Kar and Kanoria [9] and Yousef [10]. Pal et al. [5, 14] studied the effect of homogeneity of the surface waves in anisotropic media.
In this paper, the stress distributions and temperature variation has been depicted in an anisotropic triclinic half space for G-N model II and III both with rotation.
2. Basic equations
For a linear thermoelastic anisotropic body subjected to rotation the field equations are as follows:
The equation of motion in the absence of inner heat source:
Heat – conduction equation in absence of body force:
The Duhamel-Neumann stress-strain relations are:
where
Strain – displacement relation:
where the differentiation with respect to space variable is denoted by and that with respect to time is denoted by notation.
3. Formulation of the problem
Let us consider a linear anisotropic thermoelastic half space within for a time dependent heat source on the boundary plane to the surface 0. The surface is assumed to be traction free and the body is assumed initially at rest. The components of displacement vectors of three dimensional plane waves in anisotropic elastic medium, are given as:
where is the time variable and , denotes the respective orthogonal Cartesian co-ordinate axes. The elastic medium is now considered as rotating uniformly with an angular velocity , where is the unit vector along the direction of rotation. The equation of motion of the rotating frame contains two additional terms: (×(×) representing the centripetal acceleration due to time varying motion only and (2×) representing the coriolis acceleration and (1, 0, 0).
Using Hook’s law, the stress- strain- temperature relations can be written as follows:
In absence of inner heat source and body force the equation of motion are given as:
With the help of Eqs. (5) and (6), the equations of motions Eq. (7) become:
The generalized heat-conduction Eq. (2) is written as:
The following non- dimensional variables are introduced to transform the above equations in non-dimensional form:
where is some standard length.
Using Eq. (10), the non dimensional forms of the Eqs. (8a)-(9) reduces to (omitting primes for convenience):
where:
Non – dimensional stress components can be calculated as:
4. Normal mode analysis
The physical variables are decomposed in terms of normal modes to obtain the solution of (11) and (12) (Sarkar and Lahiri [13]) in the following form:
where , being angular frequency and , are the wave numbers are and along and directions respectively.
Using Eq. (14) in Eqs. (11)-(13), we obtained (omitting ‘*’ for convenience):
where , , , and are given in Appendix I.
Equations (15)- (18) can be written in the vector- matrix differential equations (Sarkar and Lahiri [13]) as follows:
where:
where and are null matrix and identity matrix of order 4×4 and and are given in the Appendix I.
5. Solution of the vector- matrix differential equation: eigenvalue approach
Applying eigenvalue approach method as in Santra et al. [15] to solve the vector-matrix differential equation (25), we get the characteristic equation of the matrix as:
The roots of the Eq. (26) are of the form:
The eigenvector corresponding to the eigenvalue can be calculated as:
where , are given in the Appendix I.
The eigenvector corresponding to the eigenvalue can be calculated from equation (27). For our further reference, we use the following notations:
As in Lahiri et al. [12], the general solution of Eq. (25) which is regular as can be written as:
where the arbitrary constants are to be determined from the boundary conditions of the problem and because of regularity condition of the solution at the terms containing exponential of growing nature in the space variables have been neglected.
Thus, the field variables can be written from the Eq. (29) for as:
6. Boundary conditions
To determine the arbitrary constants , boundary conditions are considered at the surface on the half space as in Sarkar and Lahiri [13].
Mechanical boundary condition: On the traction, free boundary of the half-space:
Thermal boundary condition:
Since, , we get at , where is the normal components of the heat flux vector, is the Biot’s number, corresponding thermally insulated boundary, corresponding to isothermal boundary. is the intensity of the applied heat source.
With the help of Eq. (14), Eqs. (37) and (38) become (omitting ‘*’ for convenience):
7. Numerical analysis
For the purpose of illustrating the problem, we now consider a numerical example for which computational results are presented. Since is complex, we take , for studying the effect of wave propagation, we use the following physical parameters in SI units given in the following.
The numerical constants are given by:
Variations of the stress components and temperature distribution has been graphically shown from Fig. 1 to Fig. 7 for G-N model of type III comparing with G-N model of type II with rotation and without rotation with respect to for the constant values of 0.5 and 0.2.
(1) The nature of the stress component is contraction in nature for G-N model of type II and III with rotation 25 whereas without rotation stress is parallel to the axis. Stresses for G-N model type II and III are same and parallel in and then gradually decreasing.
(2) Fig. 2 shows that the stress component is extensive in nature. The maximum value occurs for G-N model of type III with rotation. Stresses are gradually increasing in and then decreasing.
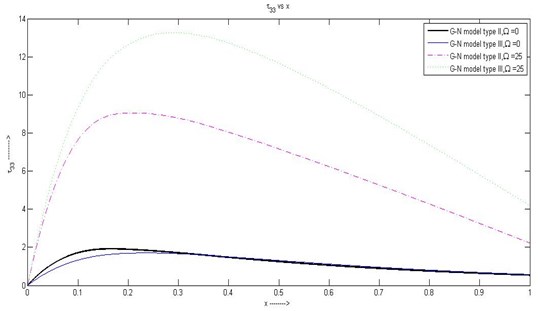
(3) Nature of the stress is same as .
Fig. 1Variation of τ11 with respect to x1 with rotation and without rotation
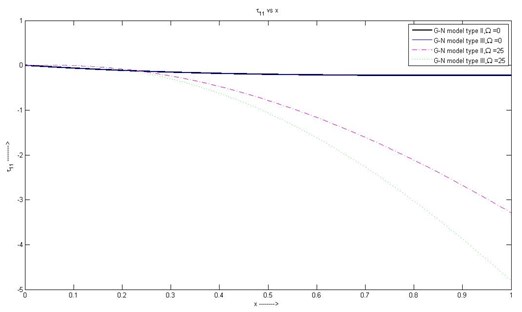
Fig. 2Variation of τ22 with respect to x1 with rotation and without rotation
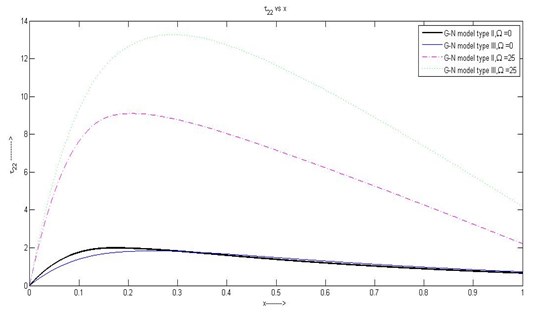
Fig. 3Variation of τ33 with respect to x1 with rotation and without rotation
(4) In Fig. 4 nature of the stress component is same for G-N model II and III without ritation. Small variation can be seen for the case of with rotation in the range . and then stresses are gradually decreasing for all the four cases.
(5) In Fig. 5 nature of is same as for the case of without rotation. And for the case of with rotation the stresses are parallel to the axis except for a small variation in the range in case of G-N model type III.
Fig. 4Variation of τ12 with respect to x1 with rotation and without rotation
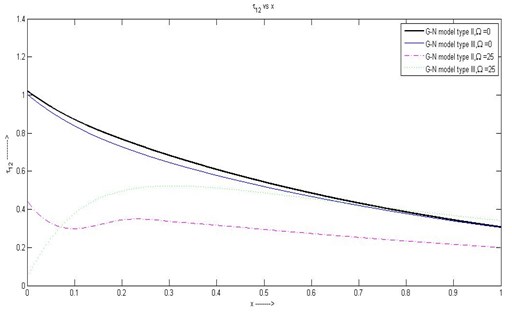
Fig. 5Variation of τ13 with respect to x1 with rotation and without rotation
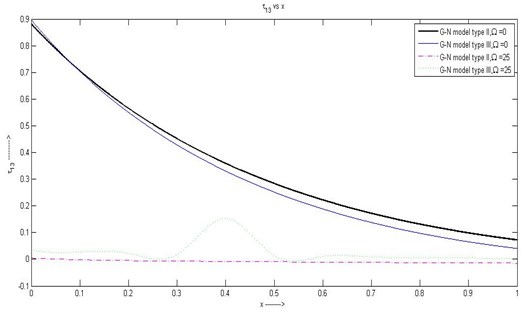
Fig. 6Variation of τ23 with respect to x1 with rotation and without rotation
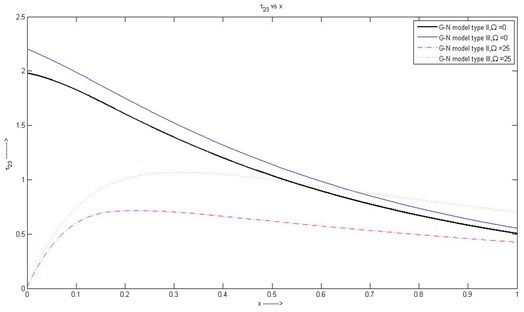
(6) Fig. 6 shows that initial value of for G-N model type II and III with rotation is 0 for whereas without rotation the initial values are 2 and 2.2 for G-N model II and III respectively. In the range , the stress component monotonically decreases without rotation whereas it increases initially starting from 0, attains a maximum value and then gradually decreases with rotation.
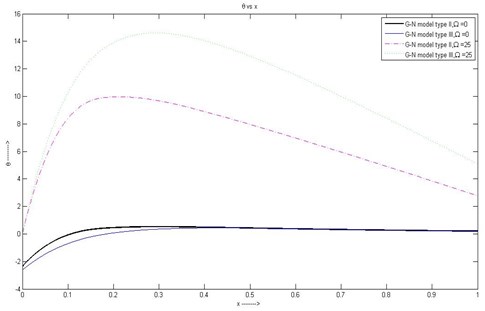
(7) From Fig. 7 we can see that the temperature is gradually increasing in and then maximum value occurs at 0.2 for the case of G-N model type III with rotation and after that temperature for all the four cases are gradually decreasing.
Fig. 7Variation of θ with respect to x1 with rotation and without rotation
8. Conclusions
Thermal stresses and temperature on a traction free boundary in a half space for G-N model type II as well as type III due to time dependent heat source shows significant dependence on rotation as evident from the above curves.
Various stress components deviate under rotation from their rotation less counter parts. Certain stress component possesses non zero initial value when subject to rotation whereas for temperature a converse effect has been found.
References
-
Biot M. A. Thermoelasticity and irreversible thermodynamics. Journal of Applied Physics, Vol. 27, 1956, p. 240-253.
-
Ignaczak J. Uniqueness in generalized thermoelasticity. Journal of Thermal Stresses, Vol. 2, 1979, p. 171-175.
-
Dhaliwal R. S., Sherief H. H. Generalized thermoelasticity for anisotropic media. Quarterly of Applied Mathematics, Vol. 33, 1980, p. 1-8.
-
Ignaczak J. A note on uniqueness in thermoelasticity with one relaxation time. Journal of Thermal Stresses, Vol. 5, 1982, p. 257-263.
-
Pal P. K., Acharya D. Effect of inhomogeneity on the surface waves in anisotropic media. Sadhana, Vol. 23, 1998, p. 247-258.
-
Green A. E., Naghdi P. M. A re-examination of the basic postulate of thermomechanics. Proceedings of the Royal Society of London A, Vol. 432, 1991, p. 171-194.
-
Green A. E., Naghdi P. M. On undamped heat waves in an elastic solid. Journal of Thermal Stresses, Vol. 15, 1992, p. 253-264.
-
Green A. E., Naghdi P. M. Thermoelasticity without energy dissipation. Journal of Elasticity, Vol. 31, 1993, p. 189-208.
-
Kar A., Kanoria M. Thermoelastic interaction with energy dissipation in an infinitely extended thin plate containing a circular hole. Far East Journal of Applied Mathematics, Vol. 24, 2006, p. 201-217.
-
Youssef H. M. On a theory of two temperature – generalized thermoelasticity. IMA Journal of Applied Mathematics, Vol. 71, 2006, p. 383-390.
-
Abd-Alla A. M., Abo-Dahab S. M. Time-harmonic sources in a generalized magnetothermoviscoelastic continuum with and without energy dissipation. Applied Mathematical Modeling, Vol. 33, 2009, p. 2388-2402.
-
Lahiri A., Das N. C., Sarkar S., Das M. Matrix method of solution of coupled differential equations and its application to generalized thermoelasticity. Bulletin of Calcutta Mathematical Society, Vol. 101, 2009, p. 571-590.
-
Sarkar N., Lahiri A. A three dimensional thermoelastic problem for a half- space without energy dissipation. International Journal of Engineering Science, Vol. 51, 2012, p. 310-325.
-
Pal P. C., Kumar S., Mandal D. Wave propagation in an inhomogeneous anisotropic generalized thermoelastic solid. Journal of Thermal Stresses, Vol. 37, 2014, p. 817-831.
-
Santra S., Das N. C., Kumar R., Lahir A. Three dimensional fractional order generalized thermoelastic problem under effect of rotation in a half space. Journal of Thermal Stresses Vol. 38, 2015, p. 309-324.
About this article
The authors are thankful to DST-Purse Programme of the Department of Mathematics, Jadavpur University, Kolkata 700032.
