Abstract
A weak solution of free vibration is developed for multi-span beams, which can adapt general elastic boundary and coupling conditions. Firstly, create the energy functional of the multi-span beam system based on the small deformation theory. Then, adopt the modified Fourier series method to rewrite the displacement functions. Compared with the traditional Fourier series method, the present series representations provide a solution for general elastic restrains. Lastly, combined with the Rayleigh-Ritz technique, all the series expansion coefficients can be obtained as the generalized coordinates. Numerical results demonstrate that the current weak solution has good convergence and high accuracy compared with the existing results in literature and FEM results.
1. Introduction
Beams have been applied in many filed such as aerospace, marine, construction industry due to their excellent engineering features. And in some specific field, the multi-span beam structures are also used widely, such as bridge engineering, water conservancy projects, etc. As a result, over the years, the vibration of the beam and multi span beam structure characteristics has always been the hot spot of the scholars’ concerned problem.
As so far, many scholars have proposed a number of computational techniques for multi-span beams. Zheng et al. [1] apply the assumed modes method to study the vibration of a multi-span non-uniform beam subjected to a moving load. Wang [2] presents a method of modal analysis to investigate the forced vibration of multi-span Timoshenko beams with clamped boundary condition and rigid joint. The vibration of a multi-span non-uniform bridge subjected to a moving vehicle is analyzed by Cheung et al. [3] using the assumed modes method. Based on the modal analysis method and the direct integration method, Dugush et al. [4] and Ichikawa [5] study the dynamic behavior of multi-span non-uniform beams. Lin and Chang [6] deal with the free vibration analysis of a multi-span beam with an arbitrary number of flexible constraints by using the transfer matrix method. Li and Xu [7] present an exact Fourier Series method to study the vibration analysis of multi-span beam systems. Lin and Tsai [8] use the finite element method to analyze free vibration analysis of a uniform multi-span beam carrying multiple spring-mass systems. Hong and Kim [9] present an exact modelling and modal analysis method for non-uniform, multi-span beam-type structure supported and/or connected by resilient joints with damping. Marchesiello [10] presents an analytical approach to study the dynamics of multi-span continuous straight bridges subject to multi-degrees of freedom moving vehicle excitation. Johansson et al. [11] present a closed-form solution for evaluating the dynamical behavior of a general multi-span Bernoulli–Euler beam by using mode superposition method. Lin [12] employs the numerical assembly method (NAM) to determine dynamic behavior of a multi-span uniform beam carrying a number of various concentrated elements.
In this paper, the authors present a weak solution for free vibration of multi-span beams subjected to general elastic boundary and coupling conditions. The general elastic boundary and coupling constraints of the multi-span beams are realized by applying the artificial stiffness-like spring technique. Based on the modified Fourier series method, each of displacements is written as a form of a standard one-dimensional Fourier cosine series with several auxiliary functions. The series expansion coefficients are obtained by using the Rayleigh-Ritz technique. The accuracy and convergence of the current weak solution is checked by comparing with the existing results in literature and FEM results.
2. Theoretical formulations
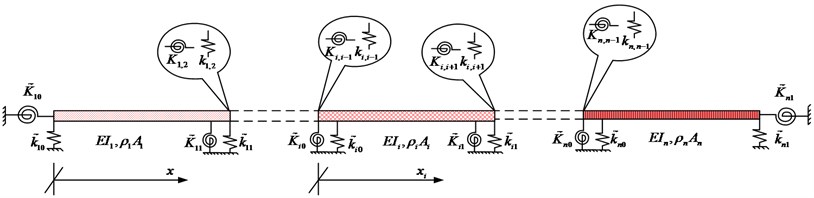
A multi-span beam system is shown as Figure.1. The system includes multiple beams which are coupled with joints. Each joint consists of two group springs which are linear and rotational springs respectively. The effects of non-rigid or resilient connectors are allowed in using the coupling springs between two adjacent beams. When the stiffness of these springs become considerably larger than the bending rigidities of the involved beams, it turns to be a conventional rigid connector. Each of beams are supported by a set of elastic restraints at both ends. By adjusting the spring stiffness values from zero to infinite, different boundary conditions including traditional intermediate supports and classical boundary conditions (i.e., the combinations of the simply supported (S), free (F), and clamped end conditions (C)) can be obtained.
Fig. 1Multi-span beam system with general boundary conditions
The differential equation for the vibration of the th beam can expressed as:
where is the angular frequency of the beam, , , and are the displacement function, bending rigid, the cross-sectional area and the density of the beams, respectively.
From the previous reviews, in this study, the artificial stiffness-like spring technique is adopted to simulate the arbitrary boundary conditions and continuity conditions. With this method, the boundary and continuity conditions can be expressed as follows:
At 0:
At :
At the left end (of the first beam):
At the right end (of the th beam):
where refer to Fig. 1, denote the stiffnesses of the linear coupling springs in –directions, and denote the stiffnesses of the rotational coupling springs at the junction of beams and , respectively; and are the stiffnesses of linear boundary springs, and , the stiffnesses of the rotational boundary springs at the left and right ends of beam , respectively.
For the multi-span beams, the total strain energy () and kinetic energy () can be expressed as:
where and are represent the strain energy and kinetic energy of the th beams, and is the potential energy expression in the connective springs related to thand th beams. The detailed expression of the , and can be written as:
The Lagrangian for the multi-span beams can be generally expressed as:
The traditional Fourier series is a well-known form of admissible function for its excellent convergence. However, it is only available to some very simple boundary conditions and would a modified Fourier series technique proposed by Li [13, 14] is widely used in the vibrations of plates and shells with different boundary conditions by Rayleigh-Ritz method. Thus, in this formulation, the modified Fourier series technique is adopted and extended to investigate the free vibrations of multi-span beams with general elastic boundary and coupling conditions:
where , and are the unknown Fourier coefficients of one-dimensional Fourier series expansions for the displacements functions, respectively.
Then, substituting Eq. (16) into the Lagrangian function Eq. (15) and taking its derivatives with respect to each of the undetermined coefficients and making them equal to zero:
The problem will be transformed into an eigenvalue and eigenvector problem, and the following governing eigenvalue equation in the matrix form can be achieved:
where is the stiffness matrix for the beam, and is the mass matrix.
For conciseness, the detailed expression for sub-stiffness and sub-mass matrices will not be shown here. By solving the Eq. (18), the frequencies (or eigenvalues) of multi-span beams can be readily obtained and the mode shapes can be yielded by substituting the corresponding eigenvectors into series representations of displacement components.
3. Case studies
Free vibration of three-span beams with elastic boundary and coupling conditions are researched through the present weak solutions. The related geometrical and material parameters of the following case are given in Table 1.
Table 1A list of beam parameters and material properties
Variables | Beam 1 | Beam 2 | Beam 3 |
(m) | 1.0 | 1.5 | 2.0 |
(m2) | 5×10-5 | 1.5×10-5 | 5×10-5 |
(m4) | 10-10 | 5×10-11 | 10-10 |
(GPa) | 207 | 207 | 207 |
(kg/m3) | 7800 | 7800 | 7800 |
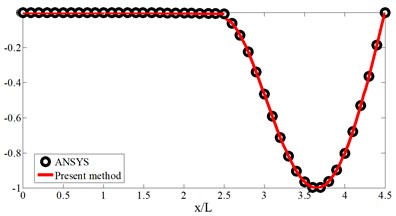
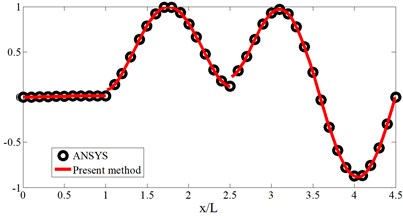
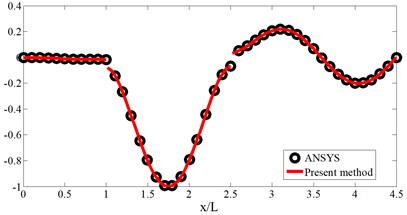
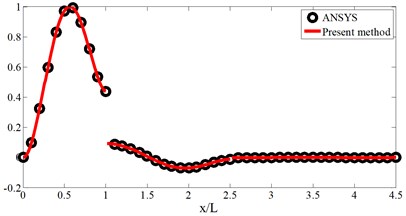
The schematic diagram, geometrical and material parameters of three-span beam are shown in Fig. 2 and Table 1, respectively. Table 2 gives the corresponding stiffness of the boundary and coupling springs with refer to the Fig. 2. Also, the Table 3 gives the convergence and validation study. In the FEM mode, the element type and mesh size are the beam 188 and 0.1 m, respectively. The mode shapes for the first four modes are plotted in Fig. 3. From the Table 3 and Fig. 3, it is obvious that the present weak solution is not only available to solve the multi-span beams with elastic boundary and coupling conditions, but also has a good accuracy and reliability.
Table 2Stiffness values for the boundary and coupling springs of a three-beam system
Spring constants for beam 1 | Spring constants for beam 2 | Spring constants for beam 3 | Spring constants for joints |
1010 N/m 5000 N/m | 4000 N/m 4000 N/m | 5000 N/m 1010 N/m | 1000 N/m 1000 N/m |
1010 Nm/rad | 1000 Nm/rad | 2000 Nm/rad | 200 Nm/rad |
2000 Nm/rad | 1000 Nm/rad | 0 Nm/rad | 200 Nm/rad |
Fig. 2Schematic diagram of three-span beam
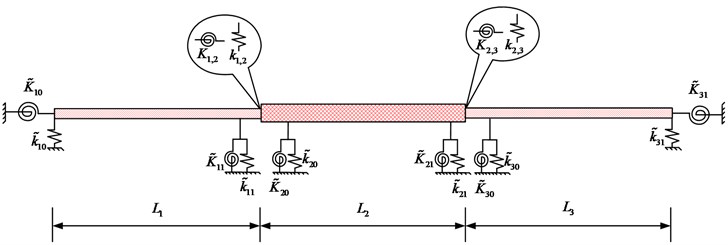
Table 3The six lowest natural frequencies for various numbers of terms in Fourier series under the three-span beam
Mode | Present Method | Exact solution | FEM | ||||
6 | 8 | 10 | 12 | 15 | |||
1 | 4.3676 | 4.3675 | 4.3675 | 4.3675 | 4.3675 | 4.3675 | 4.3675 |
2 | 13.640 | 13.640 | 13.639 | 13.639 | 13.639 | 13.646 | 13.646 |
3 | 13.833 | 13.833 | 13.833 | 13.833 | 13.833 | 13.848 | 13.848 |
4 | 21.690 | 21.690 | 21.690 | 21.690 | 21.688 | 21.689 | 21.689 |
5 | 26.698 | 26.696 | 26.696 | 26.696 | 26.695 | 26.697 | 26.697 |
6 | 34.327 | 34.323 | 34.323 | 34.322 | 34.322 | 34.325 | 34.325 |
Fig. 3The four-mode shape for the three-span beam
4. Conclusions
In this paper, a weak solution of free vibration is developed for multi-span beams, which can be applied with general elastic boundary and coupling conditions. Each of displacements is written as a form of a standard one-dimensional Fourier cosine series with several auxiliary functions. The introducing of these functions is to eliminate the discontinuities of all the related displacements and their derivatives at the ends and to improve the convergence speed of the series representations. Combined with the Rayleigh-Ritz technique, all the series expansion coefficients can be obtained as the generalized coordinates. The numerical results show that the current weak solution has good convergence and high accuracy compared with existing results in literature and FEM results.
References
-
Zheng D., et al. Vibration of multi-span non-uniform beams under moving loads by using modified beam vibration functions. Journal of Sound and Vibration, Vol. 3, Issue 212, 1998, p. 455-467.
-
Wang R.-T. Vibration of multi-span Timoshenko beams to a moving force. Journal of Sound and Vibration, Vol. 5, Issue 207, 1997, p. 731-742.
-
Cheung Y., et al. Vibration of multi-span non-uniform bridges under moving vehicles and trains by using modified beam vibration functions. Journal of Sound and Vibration, Vol. 3, Issue 228, 1999, p. 611-628.
-
Dugush Y., Eisenberger M. Vibrations of non-uniform continuous beams under moving loads. Journal of Sound and Vibration, Vol. 5, Issue 254, 2002, p. 911-926.
-
Ichikawa M., Miyakawa Y., Matsuda A. Vibration analysis of the continuous beam subjected to a moving mass. Journal of Sound and Vibration, Vol. 3, Issue 230, 2000, p. 493-506.
-
Lin H.-P., Chang S. Free vibration analysis of multi-span beams with intermediate flexible constraints. Journal of Sound and Vibration, Vol. 1, Issue 281, 2005, p. 155-169.
-
Li W. L., Xu H. An exact Fourier series method for the vibration analysis of multispan beam systems. Journal of Computational and Nonlinear Dynamics, Vol. 2, Issue 4, 2009, p. 021001.
-
Lin H.-Y., Tsai Y.-C. Free vibration analysis of a uniform multi-span beam carrying multiple spring-mass systems. Journal of Sound and Vibration, Vol. 3, Issue 302, 2007, p. 442-456.
-
Hong S.-W., Kim J.-W. Modal analysis of multi-span Timoshenko beams connected or supported by resilient joints with damping. Journal of Sound and Vibration, Vol. 4, Issue 227, 1999, p. 787-806.
-
Marchesiello S., et al. Dynamics of multi-span continuous straight bridges subject to multi-degrees of freedom moving vehicle excitation. Journal of Sound and Vibration, Vol. 3, Issue 224, 2999, p. 541-561.
-
Johansson C., Pacoste C., Karoumi R. Closed-form solution for the mode superposition analysis of the vibration in multi-span beam bridges caused by concentrated moving loads. Computers and Structures, Vol. 119, 2013, p. 85-94.
-
Lin H.-Y. Dynamic analysis of a multi-span uniform beam carrying a number of various concentrated elements. Journal of Sound and Vibration, Vol. 1, Issue 309, 2008, p. 262-275.
-
Li W. L. Free vibrations of beams with general boundary conditions. Journal of Sound and Vibration, Vol. 4, Issue 237, 2000, p. 709-725.
-
Li W. L. Comparison of Fourier sine and cosine series expansions for beams with arbitrary boundary conditions. Journal of Sound and Vibration, Vol. 1, Issue 255, 2002, p. 185-194.
