Abstract
Two methods (equivalent force method and segmental mode assuming method) of calculating the natural frequencies and mode shapes of a free-free-multi-supported beam subjected to an axial load is found, considering the structure characteristic of the guide bar, which has long length but small section, and supported by many bearings. The calculation shows that these two methods are convenient for computer programing and have the same results in obtaining the natural frequencies and mode shapes of a free-free-multi-supported beam subjected to an axial load, solving the problem that the vibration function of this kind of beam is hard to deal with because it cannot be simplified with the boundary condition of two ends. Then the segmental mode assuming method is used to analyze the impact of the support location on the natural frequencies and mode shapes of the guide bar. The relation graphs of the natural frequencies with support location, as well as the support locations where the natural frequencies reached the maximum and the minimum are found, providing a reference for the support location selection for the guide bar. The changing curves of the mode shapes with support location are plotted, which show that the bending deformation is homogeneous when the length of each segment is approximately equal, avoiding the phenomenon that bending stresses concentrates at the large-amplitude segments and cause breakage while less stress exists in small-amplitude segments and hinder the exploiting of their performance, providing a reference for the structure design of the guide bar.
1. Introduction
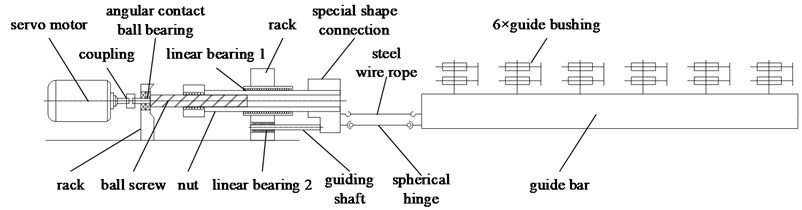
The guide bar shogging system was composited of servo motor, ball screw, spherical hinge, steel wire rope, guide bar and supporting elements, as showed in Fig. 1. Servo motor drives the ball screw, pushes out the guide bar through spherical hinge and hauls it back through steel wire rope. Guide bar with long length but small section, supported by many bearings, will vibrate under high speed movement, which influents the movement smoothness, causes transverse error, leads to “needle rubbing” phenomenon, and hinders the high speed development of warp knitting machine [1, 2].
Fig. 1The structure of the guide bar shogging system
After analyzing the model of guide bar, as showed in Fig. 2, it can be known that the guide bar satisfies the following conditions:
(1) The length of each segment (0.6 m) is more than 10 times the height of section (0.055 m).
(2) The length of a guide bushing (0.044 m) is much less than that of the guide bar (3.6 m).
(3) The transverse displacement (4×1.0583 = 4.2332 mm) can be ignored compared with the length of guide bar.
Therefore, guide bar can be considered as a free-free-multi-supported continuous beam subjected to an axial load, the main vibration form of which is bending vibration.
Fig. 2The model of guide bar

Beam is widely used in the field of aviation, mechanism and architectural engineering. The vibration of multi-supported continuous beam is often approximately calculated by energy method, iteration method and transfer matrix method [1-24]. S.-W. Hong and J.-W. Kim applied Laplace transformation to a spatial state equation and came up with the dynamic matrix for the vibration analysis of multi-span Timoshenko beams [3]. Yusuf Yesilce1et al. used secant method to obtain the frequencies values and mode shapes for the multi-span Timoshenko beam with multiple spring-mass systems [4]. D. Y. Zheng et al. analyzed the vibration of a multi-span non-uniform beam subjected to a moving load based on Hamilton principle [5]. Hai-Ping Lin et al. considered the compatibility requirements on each constraint point of Timoshenko beam and came up with the transfer matrix to deal with the free vibration analysis of a multi-span beam with an arbitrary number of flexible constraints [6]. Hsien-Yuan Lin employed the numerical assembly method (NAM) to determine the “exact” frequency–response amplitudes of a multi-span beam carrying a number of various concentrated elements and subjected to a harmonic force [8]. C. Johansson et al. applied the boundary conditions to the characteristic function of a beam and obtained its natural frequencies as well as its mode shapes, providing a closed-form solution for the vibration of continuous stepped beams under constant moving loads [9]. M. Guebailia et al. solved the free vibration equation of a multi-span bridge deck by local estimation method, and estimated the coefficients at anti nodes of the mode shapes of the beam [11]. D. ZHOU developed the static Timoshenko beam functions, which are composed of a set of transverse deflection functions and a set of rotational angle functions, and solved the vibration of a multi-span Timoshenko beam under a series of static sinusoidal loads distributed along the length of the beam [12]. H. P. Lee analyzed the dynamic response of a multi-span beam on one-sided point constraints subjected to a moving load by Hamilton’s principle and the assumed mode method [13]. WU Chongjian et al. used WPA method to obtain the dynamic response, modal shape and stress distribution of a multi-supported mast of a submarine [14].
However, most of the algorithms listed above aim at solving the vibration of hinged-hinged-multi-supported beam, and few of them involve the vibration calculation of a free-free-multi-supported beam. Also, some of the methods are too difficult for computers to calculate programmatically. Cause the displacement of two ends of a free-free-multi- supported beam isn’t fixed, the coordinate building method, as well as the vibration calculation method, is different with others. It is difficult to obtain the natural frequencies and mode shapes of a free-free-multi-supported beam because the vibration function of it cannot be simplified with the boundary condition of two ends as that of a hinged- hinged-multi-supported beam can. Two methods (equivalent force method and segmental mode assuming method) of obtaining the natural frequencies and the mode shapes of a free-free-multi-supported beam are presented based on the vibration analysis of a guide bar. The analysis shows that these two methods are convenient for computer programing and have the same results in obtaining the natural frequencies and mode shapes of a free-free-multi-supported beam subjected to an axial load. Later, the segmental mode assuming method is used to analyze the effect of supports location on frequencies and the mode shapes of the guide bar.
2. Equivalent force method
The method which replaces supports of a free-free-multi-supported beam subjected to an axial load by support constrained forces (1, 2,…, ), transforming into the problem of solving the vibration of a free-free beam subjected to an axial load and support constrained forces, is named Equivalent force method [23]. The coordinate origin point of the model should be put on the place of the first support, making the coordinate fixed, as showed in Fig. 3. The frequency equation and mode function can be derived through the vibration differential equation and constraint conditions of the beam based on this model.
Fig. 3The model of the equivalent force method

2.1. Vibration differential equation and constraint conditions in equivalent force method
The vibration differential equation of a beam subjected to an axial load is as below:
where is the impulse function. is the flexural rigidity, is the cross section area, is the length, and is the density of the beam. The location coordinate of the support is (1, 2,…, ) .
The bending moment as well as the shear force of the beam’s free ends is 0, so the boundary conditions [15, 18] are:
The displacement constraint condition:
2.2. The frequency equation and mode function in equivalent force method
The laws of the support constrained forces is the same as that of the free vibration of a beam, so let , ( 1, 2,…, ), put into Eqs. (1) and (2) and get:
where:
Implement the Laplace transformation on Eq. (4) and get:
Namely:
where:
Implement the inverse Laplace transformation on Eq. (9) and get:
where , , , are the undetermined coefficients, which are determined by the boundary conditions, is the unit step function, namely:
Take a derivative of the formula above and get:
It can be known that , , , are complex expressions containing variable and ( 1, 2,…, ), which result from the coupling of all support constrained forces. Because the coordinate origin point isn’t put on the end of the beam, Eq. (12) can’t be simplified by the boundary condition as in article [15], and unfit for computer programing. Symbol is introduced to decouple Eq. (12) based on its characteristics. is an equation containing only ( 1, 2, 3, 4; 1, 2,… or ), based on which , , , can be expressed as below:
Displacement function can be expressed as:
Substitute Eq. (11) into Eq. (7), and express the result as the form of matrix, then:
where . Because ( 1, 2, 3,…, ) are not all 0, the determinant of Eq. (12) should be 0, namely:
where:
According to the analysis above, in order to solve Eq. (16), the value of should be obtained ( 1, 2, 3, 4; 1, 2,…, ), which only need to satisfy Eq. (18). The equation is simplified and fit for computer programing:
When there are plenty of supports and the higher-order determinant is hard to solve, the converse numerical solution method can be used. Firstly, determine the range and the gradient of value . Secondly, combine , , and Eq. (10) to calculate the corresponding and , and then use Eq. (18) to obtain the value of corresponding ( 1, 2, 3, 4; 1, 2,…or ). Thirdly, put them into Eq. (16) and judge whether they are the roots of the equation set. Fourthly, put the satisfied value of into and the natural frequency can be obtained. Finally, put the calculated and the corresponding , , and into Eq. (14) and the mode shapes of the free-free-multi-supported beam can be obtained. Pay attention to the mode function Eq. (14), the second half of which are expressed by step function, and add judgement when programing.
3. The segmental mode assuming method
The method which divides the free-free beam with supports into segments at each support, assume the mode function of each segment and then create the frequency equation and mode function through boundary and connecting conditions, is called Equivalent force method. The coordinate origin point of the model should be put on the place of the first support, making the coordinate fixed, as showed in Fig. 4. The length of each segment is , , ,…, .
Fig. 4The model of the segmental mode assuming method

3.1. Vibration differential equation and constraint conditions in segmental mode assuming method
According to the general solution of the free vibration of a beam [24], the mode function of each segment of the beam is assumed as:
The bending moment as well as the shear force of the beam’s free ends is 0, so the boundary conditions are as below:
According to the continue conditions then:
Put Eq. (19) into (21) and get the Eq. (22):
3.2. The frequency equation and mode function in segmental mode assuming method
Combine Eq. (20) and (22) then:
where:
Cause the coefficients of each mode function , , , , , , , , , , , , …, , , , is not all 0, the coefficient matrix of the system of simultaneous equations:
Eq. (24) is the frequency equation of the free-free-multi-supported beam subjected to an axial load, and the coefficient matrix should meet the laws as Eq. (25).
The symbol means the submatrix extracted from the ath to bth row and the cth and dth column of matrix :
When there are plenty of supports and the higher-order determinant is hard to solve, the converse numerical solution method can be used. Firstly, determine the range and the gradient of value . Secondly, combine , , and Eq. (10) to calculate the corresponding and , and then use Eq. (25) and judge whether they are the roots of the equation set. Thridly, put the satisfied value of into and the natural frequency can be obtained. Finally, put the calculated and the corresponding , , and into Eq. (19) and the mode shape of the free-free-multi-supported beam can be obtained. The mode function Eq. (19) is also a segmented function, which can be expressed by step function as Eq. (26):
4. Vibration of the guide bar
4.1. The structure parameter of guide bar
This article takes the guide bar of a homemade warp knitting machine as the prototype, and the structure parameter of it is as below.
(1) Guide bar is made of Magnalium, of which the density 1800 Kg/m3, and the elasticity modulus 45 GPa.
Table 1The first six mode shapes of the guide bar with two methods
Equivalent force method | Segmental mode assuming method | |
The 1st mode shape | 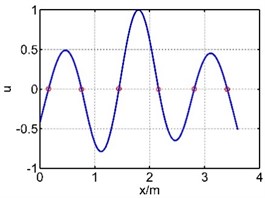 | 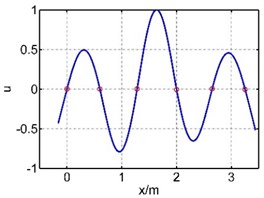 |
The 2nd mode shape | 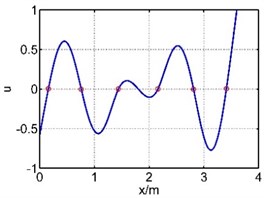 | 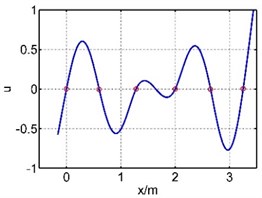 |
The 3rd mode shape | 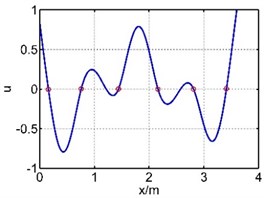 | 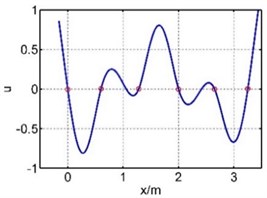 |
The 4th mode shape | 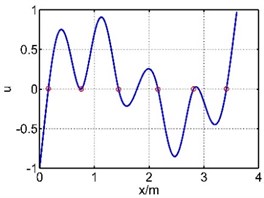 | 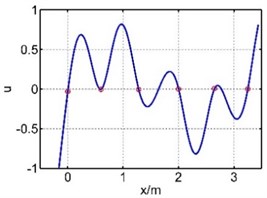 |
The 5th mode shape | 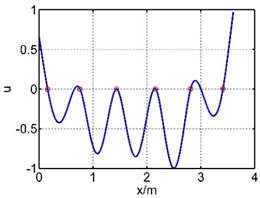 | 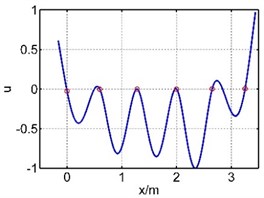 |
The 6th mode shape | 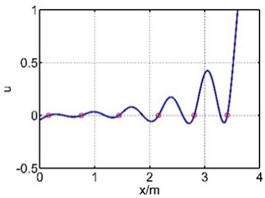 | 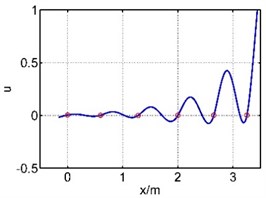 |
(2) The length of the guide bar 3.6 m. Take the end driven by spherical hinge as the beginning, then the length of each segment of the guide bar 0.16 m, 0.6 m, 0.68 m, 0.72 m, 0.65 m, 0.6 m, 0.19 m. The axial load subjected by the guide bar 5 N.
(3) The bending vibration of a guide bar will first occur in direction with the smallest cross sectional moment of inertia, and the calculated cross sectional moment of inertia 4.11×10-8 m4.
4.2. The vibration of the guide bar with equivalent force method and segmental mode assuming method
The vibration of guide bar is analyzed by the equivalent force method and segmental mode assuming method. The first six mode shapes are showed in Table 1, where is the axial coordination of the guide bar defined by each method, and u is the amplitude (by normalization processing, taking the max amplitude as 1). It can be seen from Table 1 that the 1st mode shape consists of a single half wave in each span, and the amplitude of the mid span reaches the largest. The 2nd mode shape consists of two half waves in the mid span, while the 3th mode shape in the 3th and 5th spans, the 4th mode shape in the 4th and 6th spans, the 5th mode shape in the 2th and 6th spans, the 6th mode shape in each span. The mode shape is complex depending on the material properties and support location of the guide bar.
The first six natural frequencies calculated by these two methods are showed in Table 2. It can be seen from Table 2 that the relative error of natural frequencies calculated by these two methods are within 0.1 %, which depends mainly on the gradient of value when programing, so the results are consistent. It’s obvious that both these two methods do well in obtaining the natural frequency and mode shape of the multi-supported guide bar.
Table 2The first six natural frequencies of the guide bar with two methods
Equivalent force method | Segmental mode assuming method | |
The 1st natural frequency / Hz | 113.3183 | 113.2706 |
The 2nd natural frequency / Hz | 135.2021 | 135.1958 |
The 3rd natural frequency / Hz | 157.4042 | 157.4106 |
The 4th natural frequency / Hz | 199.8986 | 200.2106 |
The 5th natural frequency / Hz | 227.9099 | 227.9576 |
The 6th natural frequency / Hz | 348.1514 | 348.1069 |
5. Analysis on the effect of support location
In the guide bar shogging system, guide bar with long length but small section, supported by many bearings, will vibrate under high speed movement, which influents the movement smoothness, causes transverse error, leads to “needle rubbing” phenomenon. Three methods are taken to increase the stiffness of the system for reducing vibration.
(1) Increase the cross-section area of the guide bar.
(2) Use high modulus and high elasticity materials.
(3) Optimize the support location of the guide bar.
Increasing the cross section area of the guide bar not only waste materials and make the system heavy, but also increase motor response time and energy consumption; Using high modulus and high elasticity materials (like Carbon fibre composite) to replace Magnalium materials not only make the production process complex but also increase the costs of the whole system; Optimizing the support location of the guide bar can reduce the vibration without adding materials, changing production process and increasing the costs. The impact of supports location on the natural frequencies and mode shapes will be studied later.
5.1. The impact of support location on natural frequencies
In the guide bar shogging system, the supports of guide bar are often arranged symmetrically for designing and assembling purposes. Use segmental mode assuming method to study the effect of the supports location and the constraint conditions are listed as below.
(1) Equality constraint:
(2) Inequality constraints:
Fig. 5First six natural frequencies change with the supports location
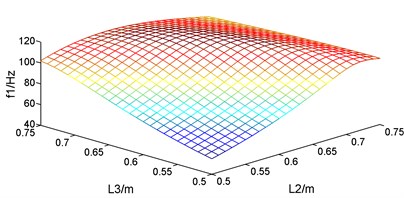
a) The 1st natural frequency
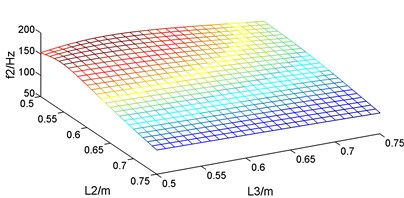
b) The 2nd natural frequency
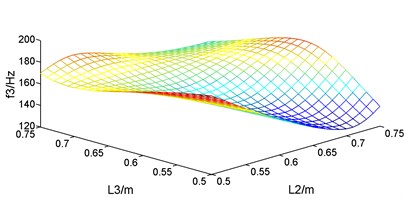
c) The 3rd natural frequency
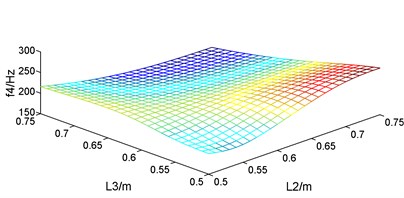
d) The 4th natural frequency
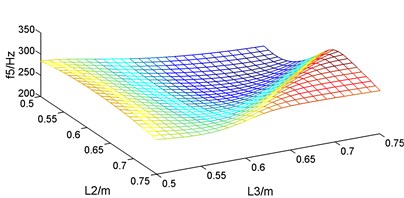
e) The 5th natural frequency
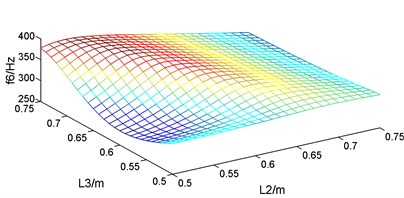
f) The 6th natural frequency
For the vibration of the guide bar, first six modes account for most of the vibration energy, so the impact of the supports location on the first six natural frequencies is studied. According to the constraints condition, guide bar is symmetric with the total length as well as the length of the two cantilever sections fixed, so when and changes from 0.5 m to 0.75 m, changes from 0.625 m to 0.25 m. Let and changes by 0.01 m, and the first six corresponding natural frequencies are plotted as Fig. 5. It can be known from Fig. 5 that the first six natural frequencies changes with the supports location within constraint conditions, but the change law is different. So, the supports location where first six natural frequencies reached the maximum and the minimum are different, too.
The supports location where the natural frequencies reach the maximum and the minimum were calculated, as showed in Table 3. It can be known from Table 3 that when the length of segment 0.50 m and 0.50 m, the 1st natural frequency of guide bar 54.8289 Hz; when 0.66 m and 0.64 m, the 1st natural frequency of guide bar researches to 116.4218 Hz, increasing the natural frequency by 2.12 times. When designing the guide bar shogging system of a warp knitting machine, the 1st natural frequency should be designed higher than the motor speed in order to avoid resonance. So, length of segment and should be designed around 0.65 m.
Table 3The supports location where the natural frequencies reach the maximum and the minimum
The 1st natural frequency | The 2nd natural frequency | The 3rd natural frequency | ||||
/ Hz | / Hz | / Hz | / Hz | / Hz | / Hz | |
116.4218 | 54.8289 | 164.8049 | 98.8352 | 192.4979 | 126.2099 | |
/ m | 0.66 | 0.50 | 0.55 | 0.75 | 0.50 | 0.50 |
/ m | 0.64 | 0.50 | 0.52 | 0.75 | 0.50 | 0.71 |
The 4th natural frequency | The 5th natural frequency | The 6th natural frequency | ||||
/ Hz | / Hz | / Hz | / Hz | / Hz | / Hz | |
263.2423 | 165.9190 | 327.3817 | 218.5197 | 386.9852 | 284.1712 | |
/ m | 0.50 | 0.75 | 0.75 | 0.72 | 0.72 | 0.60 |
/ m | 0.74 | 0.75 | 0.66 | 0.54 | 0.54 | 0.50 |
5.2. The impact of support location on mode shapes
Guide bar is made of homogenous material and has uniform section. When there is great difference in vibration amplitude among segments, bending stresses concentrates at the large-amplitude segments and cause breakage while less stress exists in small-amplitude segments and hinder the exploiting of their performance. Usually, for avoiding the fracture of the large-amplitude segments, guide bar with larger section is used, not only wasting materials, but also increasing motor response time and energy consumption.
Let and changes by 0.01 m under the constraint conditions, the corresponding mode shapes at each location are plotted in Fig. 6, where is the axial coordination of the guide bar defined by each method, and u is the amplitude (by normalization processing, taking the max amplitude as 1). It can be known from the curve that each mode in different location has similar shape but different amplitude distribution. The short segments tend to have small amplitude while long segments have large amplitude. Only when the length of each segment is approximately equal can the bending deformation be homogeneous, avoiding the stress concentrate phenomenon caused by local large amplitude. Therefore, the length of each segments should be designed roughly equal when arranging supports locations. In this case, the length of segment and should be designed around 0.65 m.
6. Conclusions
1) Two methods (equivalent force method and segmental mode assuming method) of calculating the natural frequencies and mode shapes of a free-free-multi-supported beam subjected to an axial load is found, considering the structure characteristic of the guide bar, which has long length but small section, supported by many bearings, and subjected to an axial load. The results prove that these two methods are convenient for computer programing and have the same results in obtaining the natural frequencies and mode shapes of a free-free-multi-supported beam subjected to an axial load, solving the problem that the vibration function of this kind of beam cannot be simplified with the boundary condition of two ends.
Fig. 6First six mode shapes change with the supports location
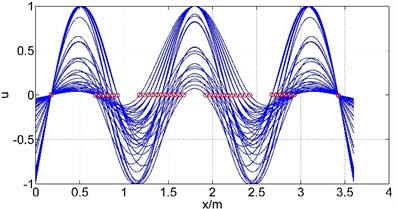
a) The 1st natural frequency
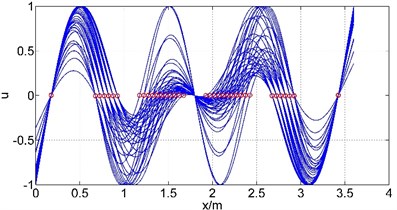
b) The 2nd natural frequency
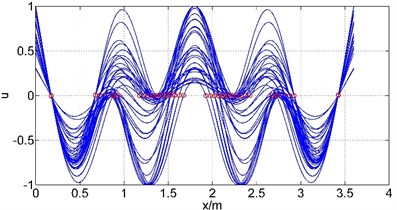
c) The 3rd natural frequency
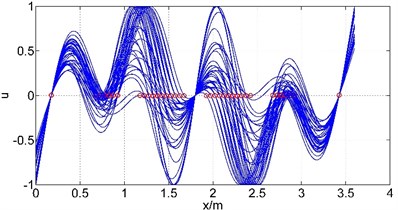
d) The 4th natural frequency
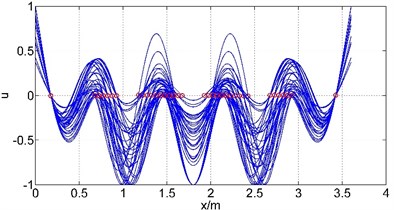
e) The 5th natural frequency
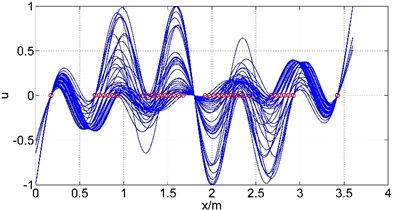
f) The 6th natural frequency
2) The segmental mode assuming method is used to analyze the impact of the support location on the natural frequencies and mode shapes of the guide bar. The graphs of the change of natural frequencies with support locations are calculated, as well as the support locations where the natural frequencies reached the maximum and the minimum, providing a reference for the support location selection for the guide bar.
3) The curves of the change of the mode shapes with support location are plotted, which show that the short segment has small amplitude while long segment has large amplitude. Only when the length of each segment is approximately equal can the bending deformation be homogeneous, avoiding the phenomenon that bending stresses concentrates at the large-amplitude segments and cause breakage while less stress exists in small-amplitude segments and hinder the exploiting of their performance, providing a reference for the structure design of the guide bar.
References
-
Xia Fenglin, Jiang Gaoming, Ge Mingqiao Moving precision analysis of electronic shogging system on high speed warp knitting machine. Journal of Textile Research, Vol. 3, Issue 3, 2009, p. 106-110.
-
Liu Nian, Xia Fenglin, Zhang Qi, Jiang Gaoming, Yin Mingyue, Qin Wen Dynamic of analysis of shogging motion of mechanism of guide bar on warp knitting machine. Journal of Textile Research, Vol. 33, Issue 11, 2012, p. 121-126.
-
Hong S. W., Kim J. W. Modal analysis of multi-span Timoshenko beams connected or supported by resilient joints with damping. Journal of Sound and Vibration, Vol. 227, Issue 4, 1999, p. 787-806.
-
Yusuf Yesilce, Oktay Demirdag, Seval Catal Free vibrations of a multi-span Timoshenko beam carrying multiple spring-mass system. Sadhana, Vol. 33, Issue 4, 2008, p. 385-401.
-
Zheng D. Y., Cheung Y. K., Au F. T. K., Cheng Y. S. Vibration of multi-span non-uniform beams under moving loads by using modified beam vibration functions. Journal of Sound and vibration, Vol. 212, Issue 3, 1998, p. 455-467.
-
Lin Hai-Ping, Chang S. C. Free vibration analysis of multi-span beams with intermediate flexible constraints. Journal of Sound and vibration, Vol. 281, Issue 1, 2005, p. 155-169.
-
Wong K. W., Lin Q., Chen J. Error detection in arithmetic coding with artificial markers. Computers and Mathematics with Applications, Vol. 62, Issue 1, 2011, p. 359-366.
-
Lin Hsien-Yuan Dynamic analysis of a multi-span uniform beam carrying a number of various concentrated elements. Journal of Sound and vibration, Vol. 309, Issue 1, 2008, p. 262-275.
-
Johansson C., Pacoste C., Karoumi R. Closed-form solution for the mode superposition analysis of the vibration in multi-span beam bridges caused by concentrated moving loads. Computers and Structures, Vol. 119, Issue 1, 2013, p. 85-94.
-
Lin Q., Chen J. A novel micro-population immune multi objective optimization algorithm. Computers and Operations Research, Vol. 40, Issue 6, 2013, p. 1590-1601.
-
Guebailia M., Ouelaa N., Guyader J. L. Solution of the free vibration equation of a multi span bridge deck by local estimation method. Engineering Structures, Vol. 48, Issue 48, 2013, p. 695-703.
-
Zhou D. Free vibration of multi-span Timoshenko beams using static Timoshenko beam functions. Sadhana, Vol. 241, Issue 4, 2001, p. 725-734.
-
Lee H. P. Dynamic response of a multi-span beam on one-sided point constraints subject to a moving load. Computers and Structures, Vol. 55, Issue 4, 1995, p. 615-623.
-
Wu Chongjian, Yang Shuzi, Luo Dongping, Zhu Yingfu The dynamic response and stress analysis of multi-supported elastic beam by use of WPA method. Journal of Huazhong University of Science and Technology, Vol. 27, Issue 1, 1999, p. 69-71.
-
Li Junqiang, Fang Tong Analysis of natural transverse vibration of continuous beam subjected to axial force. Mechanical Science and Technology, Vol. 17, Issue 4, 1998, p. 541-543.
-
Lin Q. Z., Zhu Q. L., Huang P. Z., Chen J. Y., Ming Z., Yu J. P. A novel hybrid multi-objective immune algorithm with adaptive differential evolution. Computers and Operations Research, Vol. 62, 2015, p. 95-111.
-
Chen J. Y., Lin Q. Z., Hu Q. B. Application of novel clonal algorithm in multi objective optimization. International Journal of Information Technology and Decision Making, Vol. 9, Issue 2, 2010, p. 239-266.
-
Liu Xiangyao, Nie Hong, Wei Xiaohui Vibration model for multi-span beam with arbitrary complex boundary conditions. Journal of Beijing University of Aeronautics and Astronautics, Vol. 41, Issue 5, 2015, p. 841-846.
-
Lin Q., Wong K. W., Chen J. An enhanced variable-length arithmetic coding and encryption scheme using chaotic maps. Journal of Systems and Software, Vol. 86, Issue 5, 2013, p. 1384-1389.
-
Chen J., Lin Q., Shen L. L. An immune-inspired evolution strategy for constrained optimization problems. International Journal on Artificial Intelligence Tools, Vol. 20, Issue 3, 2011, p. 549-561.
-
Wei W., Xu Q., Wang L., Hei X. H., Shen P., Shi W., Shan L. GI/Geom/1 queue based on communication model for mesh networks. International Journal of Communication Systems, Vol. 27, Issue 11, 2014, p. 3013-3029.
-
Wei Wei, Yang Xiao-Lin, Shen Pei-Yi, Zhou Bin Holes detection in anisotropic sensor nets: topological methods. International Journal of Distributed Sensor Networks, Vol. 21, Issue 9, 2012, p. 3216-3229.
-
Khodabakhsh Saeedi, Rama B. Bhat Clustered natural frequencies in multi-span beams with constrained characteristic functions. Shock and Vibration, Vol. 18, Issue 5, 2011, p. 697-707.
-
Shi Hanming, Huang Qibai Vibration System: Analyzing, Modeling, Testing, Controlling. Huazhong University of Science and Technology Press, Wuhan, 2013.
About this article
This project is supported by National Natural Science Foundation of China (51375084) and Research Fund for the Doctoral Program of Higher Education of China (20130075110002).
