Abstract
Nonlinear oscillations of a flexible pendulum system with the periodical excitation by two forces of different frequency are considered. Both forces are applied to an inertia center of a pendulum load. One of them is directed tangentially to the trajectory of motion, and another one coincides on a direction with tangent to the elastic line of a pendulum flexible rod. Such system is offered as a dynamic model for a vibrational regimes examination of some mechanical objects with the motion independent forms of their deformed elements. The quasilinear movement equations of their forced vibrations with the parametric excitation attributes at the both frequencies and also a purely forced vibration regime with a single frequency were obtained.
1. Introduction
A schemes complication, a components number increase in many machine constructions together with a considerable rise of their sizes leads to a motions independence of some separate units and entering into them elements. For this reason, traditionally used dynamic models at an oscillations study in machines appear not quite adequate for the description of some multistage constructions dynamics with not met earlier motions shape. In such cases it is expediently to use the mechanics objects, which are earlier not applied for the dynamic processes description in the systems with the deformed details relative motion in conditions of a multifrequency excitation.
To such models it is quite possible to refer the flexible pendulum systems, whose kinematics up to a surprise corresponds to an independent and highly important devices motion of some responsible mechanical constructions. If the similar type pendulum structures provide with the various properties in a large range concerning a character and conditions of attachment, a type and modification of an excitation vector and also an external force factors combination, it is possible to obtain thus a wide field of the dynamic model combination. Such models correspond to shapes variety of independent motion in the complex mechanical systems for which traditional models at the similar circumstances appear often untenable.
In paper [1] the nonlinear problem about physical pendulum natural oscillations with the flexible rod elastically attached relative to angular displacements in a fixed point was considered. For this system the quasilinear motion equations during its natural vibrations have been attained. Only small oscillations in conditions of the nonlinear terms exclusion were further investigated. Nonlinear oscillations of a mathematical flexible pendulum with a point mass on the rod end were in more detail explored. The model has however up on appreciably changed, acquiring one freedom degree. It permitted, in turn, an adoption the classical analytical methods to the nonlinear problem solution. In [2, 3] the gyropendulum nonlinear dynamics was studied under the same attachment requirements of the upper suspension, as in [1]. However, in [3] discussed only an inverted one with the support beneath its rotor center of mass. In the both cases mass centers of gyropendulum rotors didn’t coincide with their attachment points. In [4-7] considered a stability control of a nonlinearly heavy spring pendulum at the coincidence of the mass center with an attachment point on a flexible shaft. The contribution [8] analyzed the dynamics of astatic gyroscope under conditions of the parametric resonance. The mass center of a gyropendulum rotor didn’t coincide with an attachment point on a flexible shaft. An excitation source of gyropendulum was the rotor unbalance forces with a frequency of its rotation. In this contribution a planar movement of the flexible physical pendulum is excited by two periodical forces – transverse, directed along the tangent of its mass center trajectory and longitudinal following force acting along the tangent to the resilient rod line. In [1] the mass center of the pendulum weight is approximately coincident with its attachment point on the lower end of the rod. In this model the pendulum solid body has a long shape and its mass center doesn’t also coincide with the attachment point on the rod, as in [2]. The equatorial inertia radius that of assumed to be noticeable. Then taking into account considerable value of the pendulum weight, an inertias moment, bending the rod, could be considered as sufficiently great. It should be noted, that because of a small quantity of the excitation coefficients, the acting periodical forces amplitudes are regarded as little, but their frequencies – high and incommensurable. The last condition is connected with an exclusion of the frequencies multiple. One can result in nonlinear systems to an appearance of some additional phenomena, for example, subharmonic oscillations. It would be desirable here to part these factors and to explore the feasible phenomena independently.
2. Main part
For more distinct display of the model operation results we examine the simplest scheme from mentioned above systems – a physical pendulum with the flexible weightless rod and long solid body on the lower end. The mass center doesn’t coincide with its attachment point (Fig. 1), hence the rod has two sections: flexible and rigid . Pendulum oscillates in vertical plane relative to the fixed suspension point . The weight mass – , its inertia equatorial radius concerning the axis, perpendicular to the oscillation plane in the point – . The rod stiffness is constant along the elastic part , but relatively the angular displacements it is resiliently constrained in the suspension point , which is modeled by a spiral spring with stiffness . In the discussed problem only bending rod strains are taken into account, and longitudinal are neglected as their values are inconsiderable. Hence the weight center of mass will move on a circular trajectory [1].
Fig. 1Scheme of the physical pendulum with the flexible weightless rod
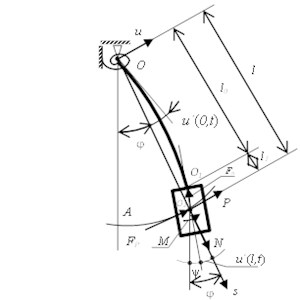
Let’s enter the necessary coordinates and variables which characterize a load position in its planar motion. The mobile coordinate system and fixed allow completely to fix a solid body motion in the pendulum oscillation plane. So, the rod angular deflection from vertically directed fixed abscissas axis and its mobile analog passing through points and determines an arrangement of the weight mass center. Angle characterizes a symmetry axis turn of the solid body, coinciding in that case with the rod curved axis tangent in the point . This angle is related with a load turn in the oscillation plane due to the elastic rod bending relatively the coordinates . Thus, both coordinates and also are necessary and sufficient for the assignment of a plane-parallel motion of the solid body in the pendulum bottom. Some words about two exciting periodical forces expressions mentioned above. Both ones are applied to weight mass center. The first is however directed tangentially to the motion trajectory and is determined by , where – small amplitude because of a little value of the excitation coefficient (it has dimensionality of an angular acceleration), and is high frequency of excitation force. Second one represents the following longitudinal force . It is directed on the rod elastic line tangent in the point and its amplitude also is small owing to the little value of the abstract excitation coefficient . Its excitation high frequency is incommensurable with for exclusion the multiplicity of both quantities. Then we form the projections expressions of the acting on the rod external forces, and also inertial ones and their moments from the pendulum load on the coordinates mobile system:
The inertial forces moment relative to the point at the load turn due to the rod bend [1]:
The positive forces directions , and moment are shown on Fig. 1. The flexure is measured from the axis directed upon a normal and it is considered as positive if it coincides with the direction [1].
Let's write down now the acting external force factors equilibrium conditions on the examined system together with the inertial forces and their moments according to a kinetostatics method:
It follows besides from the geometrical reasons the present equality:
The elastic rod flexures should satisfy to the differential equation [1]:
and the weight symmetry axis linear displacements from the axis to a geometrical relation [2]:
and to boundary conditions:
Eq. (6), (7) are caused by the weight extended shape. Its masses center a priori doesn’t coincide with the attachment point of the flexible rod weight and the expressions Eq. (6), (7) are from here arisen.
The general integral Eq. (5) has the present appearance:
and then from Eq. (6), (7), remembering about Eq. (7), the tangents slope angles to the rod curved axis in corresponding points are obtained:
where:
Being applied attentively to force structure , and parameter it is easy to notice that all they are nonlinear functions of coordinates and and their derivatives. Depending upon further applications of given materials, we suppose that the flexible pendulum angular deflections are finite, but simultaneously minor. We shall then maintain in interesting us functions all quantities up to the third order infinitesimal inclusively [1].
Expanding in the power series the trigonometrical ratios in the Eq. (1) and carrying out the necessary transforms, we obtain firstly the tangential (traverse) force:
where the linear part of one:
and its nonlinear group:
Let’s implement, however, a certain notice concerning an expression structure of the function . An infinitesimal order of the angle (the quantity, determining the rod bend), from physical reasons exclusively, below, than at – the pendulum angular deflection from the vertical. The multiplication on the small coefficient enables to recognize this term as the nonlinear element equivalent to the second order infinitesimal. This is the reason to include this product into the nonlinear terms group of . The maintenance of the similar type periodical components in this one will give an estimation major opportunity of the pendulum parametric excitation influence by the nonlinear terms with the insignificance various level.
For normal (longitudinal) force similarly it is possible to write down:
In the last expression a small periodical function , linear concerning coefficient , is formally put into nonlinear terms group . The similar step changes essentially nothing. It allows however to simplify the further expansion in a series on a small variable the subsequent necessary us functions.
We pay attention now to parameter , which according to Eq. (8) can be presented so:
further, using a binomial series, we attain:
The tangent slope angles, represent the small variable transcendental functions, as it follows from Eq. (9), (12). The last one appears, in its turn, as the second and third order infinitesmal quantity relatively , , and the small amplitude . It is, from here, obviously the expansion application in the Taylor series upon with retention only its linear terms [1, 2].
It is easy to show, that , and after a series Taylor expansion of functions , from Eq. (9) and their substitution in these expressions, taking into account Eq. (12), required derivatives will be [1, 2]:
where , .
Let’s pass to another arguments , and obtained from them constants , . Then we can write down the coefficients values , after elementaries, but labourious transforms:
The Eq. (13) seem, at first sight, coinciding with the dependences, obtained in [2] for a gyropendulum with a flexible shaft. The periodical excitation nature is however in both cases different. This phenomenon was explained in [2] by a rotor disbalance, and in our problem with the planar motion both exciting forces act in the pendulum oscillation plane, promoting the buckling and transverse bending of the elastic rod. The Eq. (14) values will therefore be others.
Let’s substitute now Eq. (10), (11), (13) in Eq. (3), (4) and, as well as earlier, after, the elementary transforms we obtain the differential motion equations of the accepted here dynamic model – the physical pendulum with the flexible rod and the rigid suspension support at the action of two periodical forces with different frequencies:
where , – dimensionless quantities.
The functions , are nonlinear concerning coordinates and their derivatives and have the present aspect:
The functions Eq. (16) in the Eq. (15) confirm just about their accessory to the quasilinear class.
The consideration of the Eq. (15) and Eq. (16) structure enables to carry out the preliminary analysis of the possible vibrating regimes in the studied system. The coordinate in the Eq. (15) linear group has the periodical coefficients with the frequency and it indicates about the parametric excitation existence. Simultaneously on both coordinates and an exclusively forced oscillations regime arises with the frequency and, thus, the structure is not free from the classical resonances by the natural and forced oscillations frequencies coincidence of the flexible physical pendulum. At the expressions Eq. (16) immediate examination it is easy to be convinced, that in them many nonlinear terms are also characterized by periodical coefficients with frequencies and . It will be necessary to determine these terms effect in the functions and in an origin of either qualitatively new, or traditional vibrational regimes for studied model. Taking into account the told considerations, to the derived Eq. (15) integration and parametric analysis will be devoted a separate paper.
3. Conclusions
The obtained non-linear equations of motion allow to explore different types of hazardous vibrations for different modes of excitation, not previously studied in relation to the flexible pendulum systems. This applies in particular to forms of both the parametric resonance and the resonance in the mode of purely forced vibrations. On the other hand, the application of considered model can be effective in studying vibrations of complex engineering structures such as for example hydraulic units of power plants, nuclear reactors, equipment for extracting isotopes out of liquids and gases, and others.
References
-
Zeytman M. F., Kushul M. Ja Nonlinear oscillations of flexible pendulums with elastic connections. Solid Body Mechanics, 1966, p. 45-53, (in Russian).
-
Kushul M. Ja Motion of gyroscope with flexible axle by action of gravity forces and elastic connections at small angles of nutation and stability of its vertical rotation. Applied Mathematics and Mechanics, Vol. 32, Issue 4, 1968, p. 553-566, (in Russian).
-
Zeitman M. F. Nonlinear oscillations of flexible vertical gyroscopic rotors. Proceedings of ENOC, Saint Petersburg, 2008.
-
Pokorny P. Control of stability of nonlinear elastic pendulum. Proceedings of ENOC, Saint Petersburg, 2008.
-
Pokorny P. Stability condition for vertical oscillation of 3-dim heavy spring elastic pendulum. Regular and Chaotic Dynamics, Vol. 13, Issue 3, 2008, p. 155-165.
-
Holm D. D., Lynch P. Stepwise precession of the resonant swinging spring. SIAM Journal on Applied Dynamical Systems, Vol. 1, Issue 1, 2002, p. 44-64.
-
Lynch P., Houghton C. Pulsation and precession of the resonant swinging spring. Journal of Physics D: Applied Physics, Vol. 190, 2004, p. 38-62.
-
Miller N. J., Shaw S. W., Oporeza-Ramos L. A., Turner K. L. Analysis of a novel MEMS gyroscope actuated by parametric resonance. Proceedings of ENOC, Saint Petersburg, 2008.
