Abstract
Changes in the dynamic state of a mechanical structure, as described by energy-related characteristics of the loads of the vibration nodes in a mechanical system, are a significant indicator of differences or changes taking place in its structure. The authors have outlined a method for analysing the fatigue degradation of mechanical structures described in terms of variations in the dynamic mobility, impedances, their real and imaginary parts and fluctuations in the strength of dynamic stiffness and the strength of the internal damping of structures expressed as a function of degradation time (the number of degrading impulse impacts). Information about the technical condition of the individual material samples have been obtained on the basis of the energy characteristics of power spectral density under degrading dynamic load. The dynamic load power distribution matrix defined as the quotient of vector of vibration rate and transposed forcing action vector. The results were presented in the form of power amplitude estimation of the dynamic stiffness forces and damping forces, changing with the ongoing samples degradation process. The variations are identified over the full scope of destruction ranging from nucleation to dominant fracturing. Such an identification is carried out by the method of experimental modal analysis and by energy-based methods with the use of a mechatronic accelerated testing station. The paper provides definitions of the related measurable measures of the process. The point is illustrated with an overview of selected strength characteristics of modern construction steel.
1. Introduction
To reflect the nature of such processes, degradation of mechanical structures has been described in terms of energy parameters. Mechanical structures are damaged wherever external impact alters structural properties while the continuous accumulation of energy elevates it beyond border values causing the destruction of a pivotal structural item.
Degradation processes in materials and building structures have an energetic dimension. Changes in the parameters of structural materials will be described by an analysis (shown as a function of degradation time) of power spectral density of damping forces (internal friction) and, separately, power spectral density of dynamic stiffness forces as well as the work of forces causing degradation determined on that basis. The destruction of node sets in a mechanical system is described by a holistic energy model of loads [1].
2. State of the structural degradation of materials
The issue of structural degradation of materials has not been fully and correctly defined to date. Strength criteria and measures used currently do not take into account the energetic measures of changes occurring in the inner structure of materials. The criteria of material effort based on the assessment of stiffness (stress) changes in a structure do not completely cover the phenomena that determine strength of materials. Familiar effort criteria of boundary conditions are based on a description of stiffness (stress) changes or on spectral decomposition of stress tensor involving the division of elastic strain energy into eigenstates peculiar to a given material. The quantity of accumulated elastic strain energy in each eigenstate was compared to critical energy in this condition and on that basis the energetic effort criterion was formulated.
Materials effort criteria formulated to date often show fragmentary nature. The methods applied currently concern various ranges of defect and destruction processes and have various application ranges. Those criteria do not take into account properties of the material and are mainly formulated for static loads and for selected conditions of dynamic loads. Recently developed Garson model being a modified Huber-Mises criterion [2], relates destruction degree to the structure of a given material. That model modified by Tvergaard and Needelman (GTN model) allows for estimations of destructive loads caused by plastic cracking. However, numeric models that are developed are based on simple tension strength tests. Wang and Chim adopted stiffness degradation as a parameter of defect accumulation, while Zhang and Hartwig proposed damping registration as a better measure than stiffness degradation [3].
The existing state of knowledge in the area of the project scope was presented by Lech Dietrich in his work: “The Process and Parameters of Constructional Material Defects” [4]. An overview of various defect measures, described in scientific literature, was presented by L. Yang, and A. Fatemi [5]. According to [4] the methods are not of a universal character. L. Dietrich predicts that „the development of experimental research into the process of constructional materials destruction will focus on searching for an appropriate, measurable measure of defects, making it possible to assess the degree of degradation in material strength properties”. Elleyin and D. Kujawski [6] adopted the total of half the dissipated energy and half the product of stress and deformation for a measure of destruction. K. Gołoś [7] adopted the sum of dissipation energy and density of elastic strain energy in tension halfcycle for destruction parameter.
Wegner T. [8] addressed the issue of energetic modelling of mechanical properties of non-linear-elastic orthotropic materials. Using a phenomenological approach, he developed an original concept of building a mathematical model for mechanical properties of orthotropic material, non-linearly elastic, with three main orthotropy directions. It is an interesting alternative to methods of multi-scale modelling, based on tests of a material and its physical properties on the micro-structural level.
The subject of energetic modelling and evolution of machine condition, mainly reflected in the energy processor model, was addressed at the Poznań University of Technology [9]). The first projects in the area of assessment of dynamic load conditions, based on analyzing the modes of operational mechanical vibrations, were pursued at the Industrial Institute of Agricultural Engineering in Poznań as early as in the 60s of the 20th century. The method of analyzing the distribution of dynamic load powers [Henryk Kaźmierczak [10-23], developed at the turn of 21st century, is a basis for the development of spatial (3-dimensional) model of interactions and transfer of dynamic load powers in real constructions. The idea of an energetic method of analyzing the process of structural degradation, the concept of energetic mode was formulated by Henryk Kaźmierczak. He published and presented the foundations of the methodology at worldwide congress sessions. International Congress on Sound and Vibration [15, 17], International Seminars of Technical Systems Degradation, Modal Analysis Schools, Machine Diagnostics Symposia, Open Seminar of the Department of Systems Vibroacustics and Biodynamics at the Poznań University of Technology. Models derived from the model of action system enable one to obtain useful information about the system, which is unavailable through other methods. Initial work was successfully carried out and it covered the issue of quantitative description (in a macro scale) of degradation process of material structure. Measures of structural changes were specified for samples of constructional materials as they were exposed to impulse loads in a stable, room temperature. The real parts of spectral profiles of load powers describe the process of structural degradation of elastic material samples, resulting from changes in the inner structure (damping) in tested material, while the imaginary parts of spectral profiles of degrading load powers describe stiffness changes of the sample, until cracking.
Similarities between the spectra of real parts, imaginary parts and dynamic mobility modules and the spectra of load powers degrading the tested mechanical systems, as well as changes of these values in the function of time of their degradation, indicate that structural degradation is determined by changes in dynamic properties, that is changes in the inner structure of material and the cracking process in tested system.
3. The concept behind the model of mechanical structure degradation
A holistic model of the load shifts which occur in the course of the degradation of a mechanical system can be described as a matrix of the spectral densities of dynamic load powers [1]:
where: – dynamic mobility matrix, –external forces impacting upon the spectral density matrix, – points of external force application, – points of the discrete stress tensor model, 1, 2, 3,.. , – long time they take to succumb to degradation process, argument of point estimates and functional values characterizing change processes in dynamic structures and the dynamical condition of the system.
A machine, treated as a complex mechanical system made of such sub-systems as drive and working equipment and supporting structure, is a mechanical system with a specific spatial distribution of mass, rigidity and damping [1].
Dynamic mobility is determined by spectral densities with account taken of frequencies of the vibrations and the impacts of the forces which degrade the structure:
The dynamic resistance of a system which undergoes changes in the course of degradation is measured by mechanical impendence which in turn can be determined by the spectral densities of impact and response signals:
The structure of a sample (i.e. all of its internal features) changes during the degradation of a system (a machine component or a material sample) taking place over degradation time .
Due to its holistic nature, the modelling of the destruction of structures entails describing their behaviour in terms of physical processes whose individual components of the matrix of the distribution of dynamic loads, which are a function of dynamic time t or frequency, are determined in the function of the long time they take to succumb to degradation. The real components of such a load provide a measure of the internal dissipation which causes the structural degradation of a structure.
The work performed by external forcing impact equals changes in stiffness and the effects of the system’s damping forces which in turn are a measure of its degradation. The value of the work performed is a function of the measures of vibration damping and amplitude.
Changes in the dynamic state of a mechanical structure described by the energetic characteristics of vibration loads provide a significant indication of the resulting alterations and changes occurring within its structure. By focusing on the imaginary and real components of the strengths of degradation forces seen as functions of frequency, changes (peak shifts) in such functions may be identified [1, 21]. Shifts in extremes frequency in the energetic characteristics offer general insights into preliminary stresses or state of degradation of mechanical structure manifested as changes in dynamic stiffness. Changing vibration damping forces, which affect the dissipation of mechanical energy, determine the structural degradation of mechanical structures over the duration of this process. An analysis of such changes allows one to define the border loads which initiate the structural degradation of mechanical structures [21].
The aim of this research is to describe the process of structural degradation of the basic technical materials, the designation of the work of degradation force work from the state of initial damage to the state directly leading to their rupture. It will also allow evaluating and predicting the general state of strain under certain loading conditions. The paper presents the general energy model of changes in dynamic multi-in – multi-out mechanical system. The basic problem of determining the measurement of the structural degradation process is presented by examining the samples of structural machine steel adopted in the study as one-in – one-out system (point 4b).
4. Degradation characteristics and examples
a) The method of energy analysis of structural degradation was used to determine characteristics of changes in structural machine elements. Modal parameters of machines were identified through systems with the following input data – operational response signals, spectral transmittance functions and impulse responses. Energy characteristics of testing loads (dynamic load powers, including powers which are internally dissipated as well as inertia force and dynamic stiffness force powers) confirm the usefulness of the energy analysis method of structural degradation to assess the degree of damage to the trailer frame exposed to degrading loads on an accelerated testing stand (Fig. 1).
Fig. 1Fraction of the right frame side member of an agricultural trailer machine

Fig. 2Comparison of characteristics ReN of changes in internal structure of trailer frame (green – before breaking)
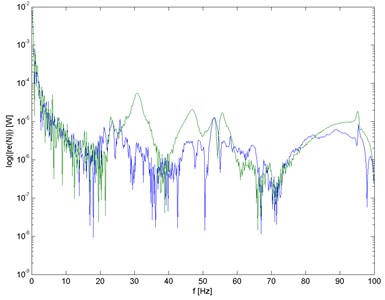
Fig. 3Comparison of characteristics ImN of trailer frame (green – before breaking)
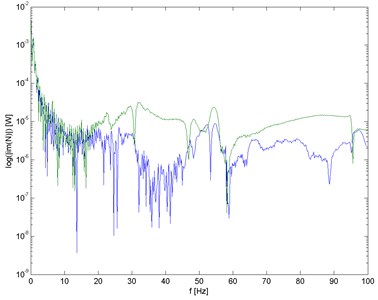
Differences in component spectra of power of test loads show changes in internal material structure as well as structural changes of the frame (Fig. 2) and changes in frame stiffness – breaking (Fig. 3).
b) The research position comprised mainly of an automated impact control unit, an electro-dynamic hammer, troughs for measuring impulse impact forces and vibration accelerations, a dual channel analyser, a computerized data transmission and retransmission system as well as a post-processor for calculating energetic values and characteristics in multi-dimensional space (Fig. 4).
Fig. 4Mechatronic system for determination of characteristic of structural degradation of mechanical objects [20]
![Mechatronic system for determination of characteristic of structural degradation of mechanical objects [20]](https://static-01.extrica.com/articles/17717/17717-img4.jpg)
The author carried out a comparative study of the fatigue strength of construction steel samples and laser weld joints of samples having the same dimensions. They determined the characteristics of the structural destruction of metal sheet samples cut with a water jet along and across rolling direction.
The characteristics of the structural destruction process of metal sheet samples cut (water jet cutting) along and across rolling direction were determined Fig. 5.
Fig. 5Photographs of fatigue cracked constructional steel samples

Destruction to the point of fracture formation took several to over twenty hours – duration time was longer for solid samples and shorter for welded ones (Fig. 6).
Relevant units of dynamic mobility and their real (Re) as well as imaginary () components, units of mechanical impendence [20] as well as their real and imaginary components and units of dynamic load power as well as their real and imaginary components were marked on a vertical axis representing structural degradation characteristics. The horizontal axes of three-dimensional graphs were used to represent frequencies (in Hertz) and degradation time (in minutes). The scaling of the degradation time axis is expressed with number n of the impulses brought to bear on each tested material sample (Fig. 6).
Graphs of the spectral densities of real load power components describe the structural degradation resulting from changes in the internal structures of the tested materials (damping). On the other hand, the graphs showing the spectra of spectral densities of the imaginary components of degradation load powers describe changes in sample stiffness to cracking point. Load power graphs are non-linear characteristics of sample degradation (Fig. 8).
In analysing the graphs of spectral density spectra depicting parts of real loads and the structural degradation of individual samples, note should be taken of changes in the components of such spectra and the new induced components of the function of the number n of degrading impulses.
Fig. 6Characteristics of structural degradation of welded steel sample
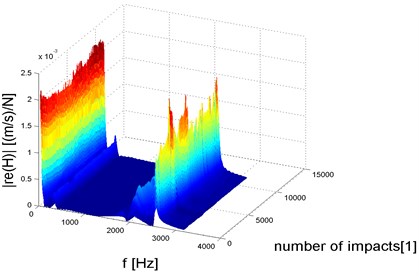
Fig. 7Changes in impedance (dynamic resistance) Rf
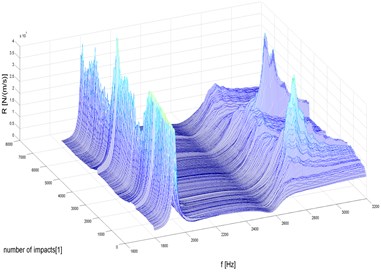
A comparison has been offered of the selected characteristics of modules, real () and imaginary () components of dynamic mobilities, impendence modules (Fig. 7), their real and imaginary components and changes in the strength of dynamic stiffness and damping forces shown as a function of process degradation time (the number of degrading impulse impacts) (Fig. 7, 8) over the full range of destruction from nucleation to dominant fracturing [23].
The number of impacts and the work of structural degradation forces vary from one construction material to another. Such characteristics include specific information on changes in the structure at hand in its degradation process until fracture.
Changes in the amplitudes of dynamic mobility and impendence modes are essential (Fig. 6, 7). The fact that the numbers of degrading load impulses and the changes in dynamic mobility and impendence mode amplitudes varied significantly has suggested substantial discrepancies in sample durability.
Fig. 8Changes in the characteristics of rigidity force powers ImNn and damping force powers ReNn causing the degradation of samples
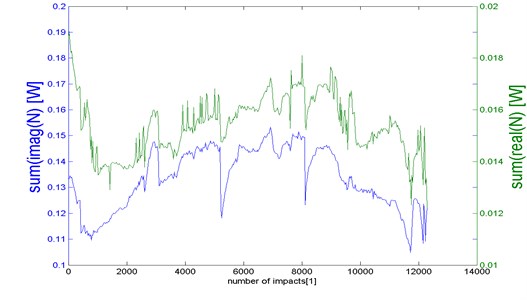
The characteristics of sample degradation take the form of impedance graphs (Fig. 7).
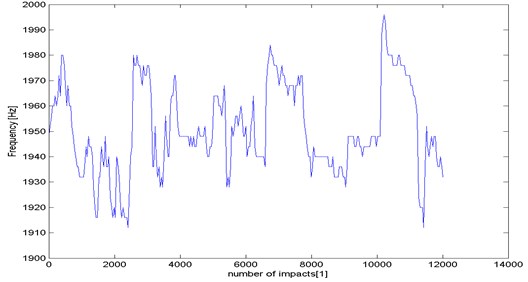
A symptom of structure degradation are changes in its dynamic properties manifesting themselves with variations in dynamic mobilities and mechanical impedances presented as a function of the number of degrading energy doses applied to the structure. Changes (declines and increases) in the frequency of dynamic characteristic modes indicate alterations in the internal structure (damping) and the dynamic stiffness of structures (Fig. 8). A case in point is an increase in mode frequency, which is symptomatic of the strengthening of material structure.
Fig. 9Periodic changes in frequency f of impendence mode ReRn
The cumulative effects of loads which degrade a mechanical structure are reflected in the curve of successive incremental growth in the work of structure degrading forces:
where: 0, 1, 2,…, – successive region of degrading impacts, – work of degrading force performed after k impacts, – unit dose of the work of structure degrading forces.
The shape of curve indicates a trend in material sample degradation (Fig. 10).
Fig. 10Comparison of graphs showing the accumulation of works which cause the structural degradation of steel samples (F4 (L= 1158 J))
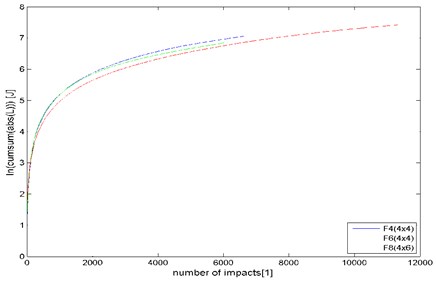
By integrating the degrading force powers function [Fig. 8] while accounting for individual impulse powers, the authors determined the work of degradation (the work of the stiffness force and the work of structural dissipation forces).
The energy degradation capacity of a material sample equals the total structural degradation work. An important measure of fatigue durability is provided by the percentage share of the work of sampling forces (which is a measure of changes in the internal structure of a material) in the total work of degradation forces. Information on the energy values of the amplitude measures of fatigue durability has found its application in construction diagnostics and specifically in the design of machinery components which are reliable in terms of their durability. For the purposes of control diagnostics, use can be made of a methodology for studying the modes of dynamic characteristics which provide a measure of changes in the properties of mechanical structures undergoing technical degradation.
5. Conclusions
1. The advantage of energy modelling of a mechanical system is that it describes the model through power which, being a composition physical value, is also composed in the domain of frequencies. As a result of synthesis, amplitude estimates of load power are obtained.
2. Similarities in spectrum shapes of real and imaginary parts, dynamic mobility modules and the spectra of loads impacting upon the mechanical systems in question, as well as changes in parameters such as a function of the number n of the applied impulses show that structural degradation depends on changes in dynamic properties, i.e. changes in the internal structure of materials leading to structure cracking.
3. Varying vibration damping, which is a factor in the diffusion of mechanical energy, is a measure of the structural degradation of a mechanical structure. Changes in dynamic stiffness, which manifest themselves with cracking, occur in the final phase of the technical degradation of a mechanical structure. An analysis of such changes facilitates the determination of border load values which trigger the structural degradation (e.g. cracking) of mechanical structure components.
4. Changes in the internal structure and structural stiffness which represent modifications of the structure’s dynamic resistance, contribute to unstable changes in process characteristics.
References
-
Kaźmierczak H. Analysis of Dynamic Load Power Distribution in Mechanical Systems. Publishing House of Poznań University of Technology, Poznań 2001.
-
Huber M. T. Strength Criteria in the Technical Effort Stereomechanics. Publishing Institute SIMP, Warszawa, 1948.
-
Zhong Zhang, Hartwig G. Relation of damping and fatigue damage of unidirectional fibre composites. International Journal of Fatigue, Vol. 24, 2002, p. 713-718.
-
Dietrich L. www.ndt-imbn.com/seminaria/03/Dep_die_03.pdf.
-
Yang L., Fatemi A. Cumulative fatigue damage mechanisms and quantifying parameters: a literature review. Journal of Testing and Evaluation, Vol. 26, Issue 2, 1998, p. 89-100.
-
Kujawski D., Ellyin F. A cumulative damage theory of fatigue crack initiation and propagation. International Journal of Fatigue, Vol. 6, 1984, p. 83-88.
-
Gołoś K. Metal fatigue strength in energetic perspective. Scientific Papers, Mechanics, Vol. 123, 1989.
-
Wegner T. M. Energetic Methods in Materials Strength. Strength Hypothesis of Inner Balance Stability. Publications of Poznań University of Technology, Poznań, 1999.
-
Cempel C., Natke H. G. Energy processors and energy transformation. System Engineering, Summer School Systems Engineering, Poznań, 1995.
-
Kaźmierczak H. Model of energy propagation in mechanical systems. Open Seminar at the Department of Systems Dynamics and Vibroacoustics at Poznań University of Technology, Poznań Vol. 23. 2000.
-
Kaźmierczak H. Load Condition Modelling in a Mechanical System. Maintenance Problems, Radom, Vol. 4, 2001.
-
Kaźmierczak H. Dynamic load power distribution in mechanical systems. Machinery Maintenance Issues Book, Vol. 3, 2001, p. 127-36.
-
Kaźmierczak H. The Role of Modal Experiment in Durability Tests of Mechanical Structures. Issues of Mechanical Structure Modal Analysis. AGH Kraków, 2003.
-
Kaźmierczak H., Pawłowski T., Cempel C. Energy flow analysis of vibration loads of machines. Eleventh International Congress on Sound and Vibration, p. 11-2004.
-
Kaźmierczak H., Kromulski J., Cempel C., Barczewski R. Energetic description of the destruction process of steel concrete structures. COST Action 534 New Materials and Systems for Prestressed Concrete Structures, Workshop of COST on NTD Assessment and New Systems in Prestressed Concrete Structures, Publishing House of the Institute for Sustainable Technologies-National Research Institute, Radom, 2005.
-
Kaźmierczak H., Pawłowski T., Kromulski J. Energetic characteristics of vibration loads on a mechanical object. 14th International Congress on Sound and Vibration, Cairns, Australia, 2007.
-
Kaźmierczak H., Pawłowski T., Kromulski J. Energetic methods in machine diagnostics. Diagnostics, Vol. 1, Issue 45, 2008, p. 109-114.
-
Kaźmierczak H., Pawłowski T., Kromulski J., Barczewski R. Energetic characteristics of prestressed concrete beams degradation. Diagnostics, Vol. 3, Issue 51, 2009, p. 59-64.
-
Kaźmierczak H., Pawłowski T., Kromulski J. Energetic modes in description of structural degradation of constructional materials. Diagnostics, Vol. 1, Issue 57, 2011, p. 25-29.
-
Kaźmierczak H., Pawłowski T. Energetic characteristics degradation of mechanical structures. International Journal of Applied Mechanics and Engineering, Vol. 17, Issue 3, 2012, p. 861-866.
-
Kaźmierczak H., Pawłowski T., Wojnilowicz Ł. Quantifiable measures of the structural degradation of constructional materials. Diagnostics, Applied Structural Health, Usage and Condition Monitoring, Vol. 14, Issue 4, 2013, p. 77-83.
-
Kaźmierczak H. Energy characteristics of dynamic degradation of mechanical structures. PIMR Poznań, 2013.
-
Kaźmierczak H., Pawłowski T., Zembrowski K. A synthesis model for forcing action arrangement inthe system for reducing dynamic loads of amobile machine. International Journal of Applied Mechanics and Engineering, Vol. 20, Issue 2, 2015, p. 437-443.
-
Akiniva Y. Stanzl-Tschegg S., Meyer H., Wakita M., Tanaka K. Fatigue strength of spring steel under axial and torsional loading in the very high cycle regime. International Journal of Fatigue, Vol. 30, Issue 12, 2008, p. 2057-2063.
-
Bannantine J. A., Comer J. J., Handrock J. L. Fundamentals of Metal Fatigue Analysis. Prentice Hall, 1989.
-
Bishop R. E. D., Johnson D. C. The Mechanics of Vibration. Cambridge University Press, 1960.
-
Cempel C., Natke H.G., Tabaszewski M. A passive diagnostic experiment with ergodic properties. Mechanical Systems and Signal Processing, Vol. 11, Issue 1, 1997, p. 107-117.
-
Cempel C. Innovative developments in systems condition monitoring, keynote lecture for DAMAS ’99. Damage Assessment of Structure Conference, Dublin, 1999.
-
Cempel C., Tabaszewski M. Multidimensional condition monitoring of machines in nonstationary operation. Mechanical Systems and Signal Processing, Vol. 21, 2007, p. 1233-1241.
-
Cempel C. Generalized singular value decomposition in multidimensional condition monitoring of machines – a proposal of comparative diagnostics. Mechanical Systems Signal Processing, Vol. 23, 2009, p. 701-711.
-
Cempel C. Decomposition of symptom observation matrix and its optimization in vibration condition monitoring of machines. Applied Mechanics and Materials, Vol. 9, 2008, p. 51-60.
-
Cempel C. The evolution of generalized fault symptoms and fault intensities as indicators of observation redundancy and coming system breakdown. Mechanical Systems and Signal Analysis, Vol. 25, 2011, p. 3116-3124.
-
DeLanghe K. High Frequency Vibration: Contribution to Experimental and Computational SEA Parameter Identification Techniques. Catholic University Leuven, 1996.
-
Dietrich L., Kowalewski Z. L. On the cyclic surface of some engineering materials under complex stress conditions. Archives of Mechanics, Vol. 50, Issue 5, 1998, p. 877-905.
-
Varrani-Farahani A. A new energy-critical plane parameter for fatigue life assessment of various metallic materials subjected to in-phase and out-of-phase multiaxial fatigue loading conditions. International Journal of Fatigue, Vol. 22, Issue 4, 2000, p. 295-305.
