Abstract
For large-scale offshore wind turbine blades, ANSYS and UG were respectively used to complete the solid modeling and the calculation of vibration modes, and the influences of the rotating speed on each order vibration mode and their main reasons were analyzed. Furthermore, the effects of material categories, the deviations of physical parameters in the process of material manufacture and structural parameters on the natural frequencies of rotating blades were respectively compared. Numerical results show that the dynamic stiffening effect of rotating blades is obvious, and the stress stiffness and the geometric stiffness play a dominant role on the natural frequencies from the first to the sixth order and from the seventh to the tenth order respectively. The influences of material categories on natural frequencies of the blades are significantly higher than those of physical parameter deviations and chord length changes. The effects of the equal amplitude increase of elasticity modulus or the chord length and the equal amplitude decrease of density on the tenth order frequency for the torsional vibration are less than those of them on the first nine orders' frequencies for the shimmy and flapping vibration, making that the increase amplitude of the blade natural frequencies first increases and then decreases with the increase of the order number. In addition, the results in this work can provide technical references for the optimization design and the further analysis of vibration characteristics of wind turbine blades.
1. Introduction
As environment and energy issues become increasingly prominent, governments and enterprises from all over the world pay more and more attention to the wind energy, which is an inexhaustible, nonpolluting and renewable energy [1]. Wind power generation is one of the main forms of wind energy utilization, while engineering practice indicates that the wind turbine blade is the most prone to malfunction. This is because the aerodynamic load acting on the blade and the centrifugal force generated by the rotation are constantly changing, and they have apparent polytropy and random [2]. When the changing frequency of wind loading, the rotating frequency of the blade and the frequency of the generator are close to the natural one of the blade structure, it's possible that the strong vibration or even the resonance for the blade will appear, which leads to the fatigue damage and the failure of mechanism, not making the blade operate safely and stably. Therefore, it’s significant to calculate and analyze the vibration modes of the blade.
Mode is an inherent vibration characteristic of mechanical structure. At present, the modal parameters of the structure such as the natural frequencies and mode shapes have been studied by using the finite element method and the experimental method. Kane et al. [3] found the phenomenon that the lateral vibration frequency of a cantilever beam attached to a moving base increased when it rotated, and put forward the concept known as dynamic stiffening. Wang and Pei [4] took the agricultural wind turbine blade for example, and analyzed the inherent vibration characteristics including flap, flutter and torsion using ANSYS. Gangeled and Ahmed [5] carried out the analysis on the natural frequency and mode shape of 1.5 MW wind turbine blade under different geometrical and material parameters without considering the dynamic stiffening effect, and then investigated the dynamic behavior characteristic of the blade. Tarfaoui et al. [6] completed the modal analysis of the 5 MW composite wind turbine blade by using ABAQUS and presented five different types of strength enhancement structure, and a comparative analysis of the various structures was carried out to select the optimal scheme to realize the lightweight of the blade. Benham et al. [7] optimized the NACA 4412 profile and performed the modal and static analysis of the blades made of carbon fiber and other three kinds of composite materials. Chen et al. [8] employed Wilson theory to develop an application program for aerodynamic design of the small blades, designed a 3 kW horizontal wind turbine blade and analyzed the influence of the material manufacturing deviation on natural vibration characteristic of the static blade. Wu et al. [9] used Wilson aerodynamic theory to design a 100 W horizontal axis blade, modified design parameters by considering vibration performance and carried out modal and pneumatic characteristic experiments. Li et al. [10] applied the Multi-body dynamics method to discuss the reason for the stiffening effect of rotating blades and analyzed the influence of the GRP anisotropy on the vibration modes of the blade.
Although there are some research advances in the analysis of the vibration modes of the wind turbine blade at home and abroad, the research on the influences of the material and its manufacturing deviations on the natural vibration characteristics of the blade under the rotating condition has not been carried out until now. To solve this problem, the dynamic characteristic equation and the entity model of the rotating blade were established in this study, and then the grid independence and the reliability verification were carried out. Furthermore, the effects of the rotating speed, material categories and different physical and structural parameters for the same material on the blade vibration modes were simulated and analyzed.
Through the modal analysis of the wind turbine blade in this work, it’s easy to check whether the resonance mode of the system is reached under different working conditions, and evaluate the influences of the possible existence of material manufacturing deviations on the safety and reliability of large-scale wind turbine blades. The change law of the blade's modal frequency with elasticity modulus and mass density is presented in this work. In the design process of the blade, the elastic modulus and mass density of the material can be taken as the main reference to select the appropriate blade material which meets the design requirements. Furthermore, under the rated rotating speed which is the most common and frequent operating condition, the natural frequencies of the blades for different materials are shown and compared, providing significant guidelines for the selection of the blade’s material.
2. Dynamic characteristic equation of the blade
After the blade is discretized by the finite element method, the motion differential equation of the structure can be obtained by using the principle of the instantaneous minimum potential energy [11]:
where u, and are the displacement, the velocity and the acceleration of the finite element node respectively. is the external force vector acting on the blade. and are respectively the mass matrix and the damping matrix. Stiffness matrix , and represent the finite element stiffness matrix for small deformation and the dynamic stiffness matrix respectively.
When the wind turbine blade rotates around the rotating shaft in a certain angular velocity, the centrifugal inertia force has an effect on the blade deformation, and the mutual coupling between the rotation and deformation leads to the change of the blade stiffness, which is known as dynamic stiffening phenomenon [12]. While calculating the vibration modes of the rotating blade, the dynamic stiffness matrix can be expressed as:
where is the stress stiffness matrix generated by the mutual coupling between the blade rigid motion and its elastic deformation, and is the geometric stiffness matrix resulted from the in-plane deformation which is caused by the centrifugal inertia force.
In Eq. (1), set , and then the blade is in free vibration state at this time. In addition, when solving the natural frequency of the blade structure, the damping effect is generally not considered, that is, . Therefore, Eq. (1) can be rewritten as:
Assume and substitute it into Eq. (3), and then the generalized eigenvalue equation of the structural dynamic problem for the blade can be described as:
where and are the eigenvalue and the eigenvector at the order respectively, and they are corresponding to the natural frequency and mode shape of the blade structure. Moreover, , and is the self-vibration frequency.
3. Numerical simulation process
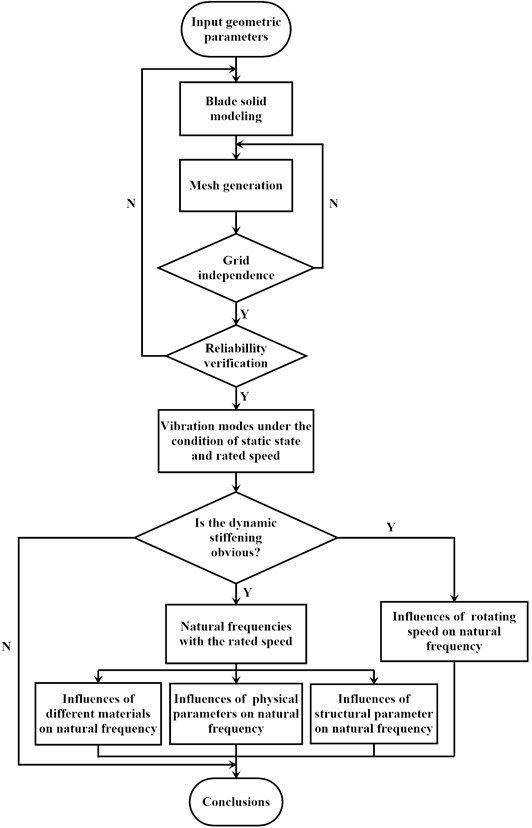
The influences of the rotating speed, different materials, and physical and structural parameters of the same material on the vibration modes for the blade under the rotating condition were analyzed in this work. The main steps are as follows: 1) The geometrical parameters of each blade element for the 5 MW offshore wind turbine, such as airfoil, chord Length and torsional angle, were obtained from the technical report released by the National Renewable Energy Laboratory (NREL), and the entity model of the blade was built by Unigraphics NX (UG). 2) The mesh generation for the entity model was carried out until the requirement for the grid independence was satisfied. 3) Compare and analyze the accuracy of the natural frequencies to verify the reliability of the numerical simulation results in this study. 4) By comparing the natural frequencies under the condition of rated rotating speed and static state, one can judge whether the dynamic stiffening effect is considered or not. 5) Give the change rules of natural frequency at each order varying with rotating speed. 6) Under the rated rotating speed, compare the natural frequencies of each order for different materials, and analyze the influences of different physical parameters of the same material and the variation of the structural parameter on the blade vibration modes. The detailed process of numerical simulation is shown in Fig. 1.
Fig. 1Flow chart of numerical simulation
4. Entity modeling and mesh generation of the blade
4.1. Entity modeling
Taking a wind turbine blade with the current installed capacity of 5MW as the research object, Ref. [13] gave the corresponding geometric data of the airfoil profile. The specific parameters are listed in Table 1. The airfoil coordinates were transformed, and UG was used to establish blade elements and curved surfaces, and then the blade solid model was built with the aid of the curve group function, as shown in Fig. 2.
Table 1Parameters of blade elements
No. | Span (m) | Chord length (m) | Torsional angle (°) | Airfoil |
1 | 2.8667 | 3.542 | 13.308 | Cylinder |
2 | 5.6000 | 3.854 | 13.308 | Cylinder |
3 | 8.3333 | 4.167 | 13.308 | Cylinder |
4 | 11.7500 | 4.557 | 13.308 | Cylinder |
5 | 15.8500 | 4.652 | 11.480 | DU40_A17 |
6 | 19.9500 | 4.458 | 10.162 | DU35_A17 |
... | ... | ... | ... | ... |
14 | 52.7500 | 2.518 | 1.526 | NACA64_A17 |
15 | 56.1667 | 2.313 | 0.863 | NACA64_A17 |
16 | 58.9000 | 2.086 | 0.370 | NACA64_A17 |
17 | 61.6333 | 1.419 | 0.106 | NACA64_A17 |
Fig. 2Entity model for the wind turbine blade

4.2. Mesh generation
The number of grid cells directly affects the accuracy of the numerical results, so it is necessary to verify the grid independence. By changing the number of grid cells, the first order natural frequencies of the blade are given in Table 2. It can be found that the first order natural frequency is convergent and the minimum relative error is only 0.41 %. Therefore, 14661 grids were chosen in this work, and the finite element model of the blade is shown in Fig. 3.
Due to the advantages of light weight, high strength and good rigidity, the glass reinforced plastic (GRP) is widely used for the commercial wind turbine blades. The corresponding material parameters are listed as follows: the density 1700 kg/m3, the elasticity modulus 17.60 GPa and the Poisson ratio 0.17.
Table 2Grid-independent validation
Number of grid cells | 5498 | 7903 | 11181 | 14661 |
First order natural frequency (Hz) | 0.1812 | 0.1901 | 0.1945 | 0.1954 |
Relative error | – | 4.91 % | 2.31 % | 0.46 % |
5. Results and discussions
5.1. Reliability verification
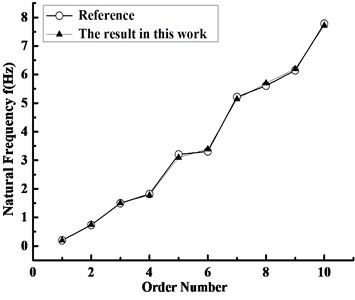
The 30 kW wind turbine blade model in Ref. [8] was selected to carry out reliability verification. The diameter of the wind wheel is 10 m, and the airfoil of the blade made of pine is NACA4412. The comparison results of the natural frequencies for the first ten orders are displayed in Fig. 4. It is very clear that the two variation curves of the natural frequency vs. the order number show a good agreement, which verifies the reliability of theoretical model and calculation program in this work.
Fig. 3Finite element model for the 5 MW wind turbine blade

Fig. 4Variation of the blade natural frequency with order number
5.2. Influences of rotation on vibration modes
5.2.1. Modal analysis of the static blade
The dynamic performance is significant to the design of the wind turbine blade. When the natural frequency of the blade is close to that of the excitation force, the resonance phenomenon will happen [14]. Thus, the modal analysis of the single blade was carried out in this work. Under the circumstances that the root of the GRP blade is fixed and the rotating speed was zero, the natural frequencies and mode shapes of the first ten orders were given in Table 3.
Table 3Natural frequencies and mode shapes of the first ten orders
Order number | Frequency () | Mode shape |
1st | 0.3745 | Flapping |
2nd | 1.0217 | Flapping, Shimmy |
3rd | 1.1999 | Flapping, Shimmy |
4th | 2.4117 | Flapping |
5th | 3.4138 | Shimmy |
6th | 4.3214 | Flapping |
7th | 6.7048 | Flapping |
8th | 7.5585 | Obvious Shimmy |
9th | 9.6499 | Flapping |
10th | 10.4260 | Obvious Torsional Vibration |
It can be seen from Table 3 that the mode shape of the first order is a pure flapping one, while the mixed form of flapping and shimmy appears in the second and the third orders. From the fourth to the ninth order, the blade basically keeps the mode shape of flapping or shimmy. The torsion mode shape appears in the tenth order, which indicates that the blade has strong anti-bending ability. According to the vibration theory, the energy of the blade vibration mainly concentrates on natural frequencies ranging from the first to the third order. Therefore, flapping and shimmy are the main vibration types of the wind turbine blade.
5.2.2. Modal analysis of the rotating blade
Under the condition of the rated rotating speed 12.1 rpm, the natural frequencies and the main mode shapes of the first ten orders were obtained, and the other conditions were identical to those of the static state. To observe the effects of the dynamic stiffening resulted from the blade rotation, the natural frequencies under static and rated rotating states are both listed in Table 4, as well as their relative errors. It can be found from Table 4 that the dynamic stiffening effect only has a significant influence on the blade natural frequencies of the first and the tenth order. What’s more, it is not obvious for the natural frequencies from the second to the ninth order, but all of them have some increase. Furthermore, the main mode shapes of the blade are plotted in Fig. 5. It can be directly seen that there are four mode shapes such as flapping, flapping and shimmy, shimmy and torsion, which is basically consistent with those of the static blade.
Table 4Natural frequencies of the first ten orders under rotating and static states (Hz)
Order number | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th | 10th |
Static | 0.3745 | 1.0217 | 1.1999 | 2.4117 | 3.4138 | 4.3214 | 6.7048 | 7.5585 | 9.6499 | 10.4260 |
Rotating | 0.1954 | 1.0276 | 1.2110 | 2.4319 | 3.5055 | 4.3751 | 6.8218 | 7.8030 | 9.9244 | 20.346 |
Relative Error | 91.66 | 0.58 | 0.93 | 0.84 | 2.69 | 1.24 | 1.75 | 3.23 | 2.84 | 95.15 |
Fig. 5Main mode shapes of the blade under rated rotating speed
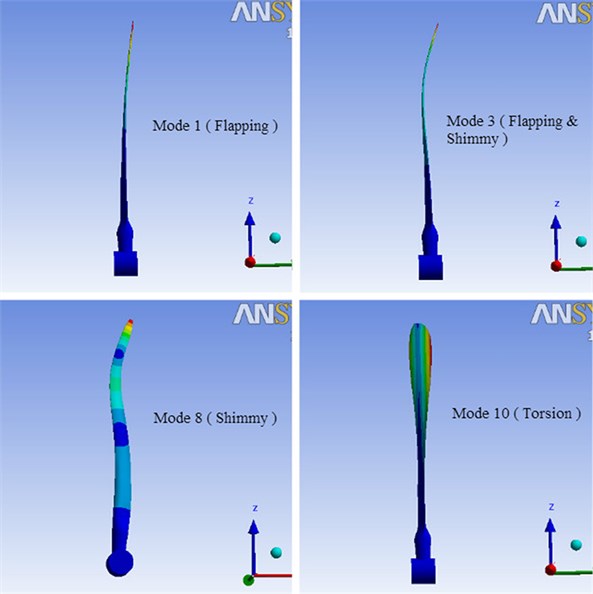
Table 5Natural frequencies of the first ten orders under different rotating speeds (Hz)
Rotational speed (rpm) | 3.5 | 6.9 | 9.5 | 12.1 | 15.0 | 20.0 |
1st | 0.3393 | 0.2742 | 0.2302 | 0.1954 | 0.1656 | 0.1298 |
2nd | 1.0313 | 1.0293 | 1.0283 | 1.0276 | 1.0271 | 1.0267 |
3rd | 1.2144 | 1.2126 | 1.2116 | 1.2110 | 1.2105 | 1.2101 |
4th | 2.4332 | 2.4325 | 2.4321 | 2.4319 | 2.4317 | 2.4314 |
5th | 3.5065 | 3.5060 | 3.5057 | 3.5055 | 3.5054 | 3.5053 |
6th | 4.3755 | 4.3753 | 4.3751 | 4.3751 | 4.3750 | 4.3750 |
7th | 6.8216 | 6.8216 | 6.8217 | 6.8218 | 6.8218 | 6.8221 |
8th | 7.8028 | 7.8029 | 7.8029 | 7.8030 | 7.8030 | 7.8031 |
9th | 9.9240 | 9.9242 | 9.9243 | 9.9244 | 9.9245 | 9.9248 |
10th | 11.6300 | 14.4480 | 17.243 | 20.3460 | 24.0240 | 30.669 |
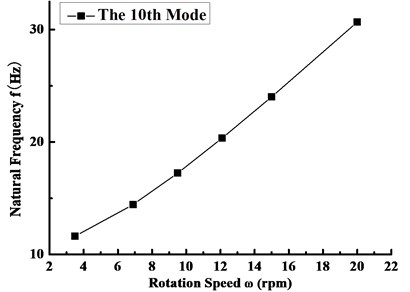
On the basis of this, the blade natural frequencies of the first ten orders under different rotating speeds are shown in Table 5. It can be found by comparing Table 5 with Table 3 that the variation trend of the natural frequency with the order number at each rotating speed is identical with that of Table 4. Furthermore, with the increase of the rotating speed, natural frequencies from the first to the sixth order for the rotating blades are all presenting a nonlinear decrease, and the reduction of the first order frequency has a certain representation, as shown in Fig. 6. This change trend is mainly derived from the stiffness weakening effect caused by the coupling between the rigid body motion and the elastic deformation of the blade, and the reduction of the stress stiffness at this time plays a dominant role. On the contrary, the natural frequencies from the seventh to the tenth order increase with the rotating speed, and the vibration of the tenth order natural frequency is the most obvious, as shown in Fig. 7. The reason is that the in-plane deformation resulted from the centrifugal inertia force makes the blade stiffness increase. At this very moment, the increase of the geometric rigidity is dominant, which leads to a slow upward trend of natural frequency.
Fig. 6Variation curve of the first order frequency with the rotating speed
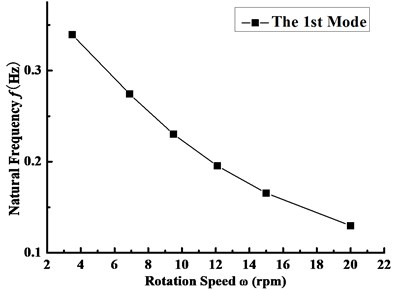
Fig. 7Variation curve of the tenth order frequency with the rotating speed
Obviously, the dynamic stiffening effect has a greater influence on the natural frequency. Therefore, the main work of this study is carried out aiming at the blade under the rotating condition.
5.3. Influences of material categories on natural frequencies
The material choice plays a key role in the design stage of the blade. It not only affects the performance and efficiency of the wind turbine, but also determines the electricity cost per kWh. Therefore, in order to avoid the appearance of resonance phenomenon, five kinds of blade materials in actual operation are selected to carry out the comparative analysis of the natural frequency here, and they are carbon fiber, bamboo, pine, aluminum and GRP respectively. All physical parameters are listed in Table 6.
Table 6Physical parameters of different blade materials
Material categories | Elastic modulus (GPa) | Poisson ratio | Density (kg/m3) |
Carbon fiber | 228.00 | 0.250 | 1780 |
Bamboo | 8.76 | 0.325 | 780 |
Pine | 8.00 | 0.300 | 430 |
Aluminum | 68.90 | 0.330 | 2700 |
For the blade under the rated rotating speed, the variation curves of the natural frequencies for different materials with the order number are plotted in Fig. 8. It is not difficult to see that the natural frequencies of carbon fiber, aluminum, pine, bamboo and GRP almost show a non-linear growth trend with the increase of the order number, and the ones at each order decrease in turn, because the natural frequency is proportional to the elasticity modulus and Poisson ratio while it has an inverse relationship with the density. The increased amplitude of natural frequencies between every two materials increases with the order number but decreases suddenly in the tenth order, which arises from the reason that physical parameters have a less impact on the torsional frequency of the tenth order than shimmy and flapping ones of the first ninth orders. Based on the discussed results mentioned above, it is of great convenience to choose the appropriate material for the blades, which will avoid the resonance region especially in the first two orders.
5.4. Influences of material physical parameters deviation on natural frequencies
In the blade manufacturing process, the material physical properties have a certain randomness [14]. Therefore, the extensive use of GRP material was taken as an example in this work, and the influences of a certain range of the deviation in elasticity modulus and mass density on the blade natural frequency were analyzed.
Fig. 8Variation of the blade natural frequency vs. the order number with different materials
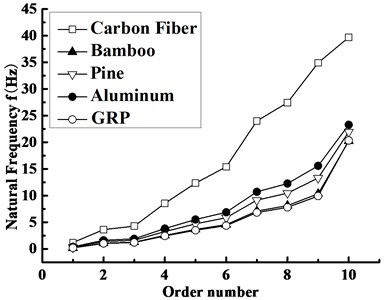
Fig. 9Natural frequencies of the blade with different elasticity modulus
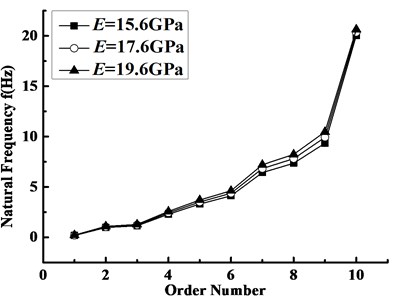
5.4.1. Deviation of elasticity modulus
The blade natural frequencies of the first ten orders within a certain deviation scope in elasticity modulus were given in Fig. 9. As you can see, when the elastic modulus increases equally, the difference value between the natural frequencies first increases and then decreases with the increase of the order number, and reaches a maximum at the ninth order. This can be interpreted as the reason that the increase of the elasticity modulus causes the increase of stiffness, and then results in the rise of the natural frequency, while there is an obvious torsional vibration at the tenth order.
5.4.2. Deviation of mass density
Similar to Fig. 9, Fig. 10 also depicts the influences of the deviation in mass density on the natural frequency. It can be observed from Fig. 10 that the deviation of mass density has a certain influence on the blade natural frequencies. When the density decreases equally, the difference between the natural frequencies shows the same trend with elasticity modulus shown in Fig. 9. The reason is that the density decrease brings about the mass reduction, which leads to the increase of the natural frequencies. Furthermore, the torsional vibration appeared at the tenth order renders the decrease of the increased amplitude of the natural frequency.
5.4.3. Influence of structural parameter on natural frequencies
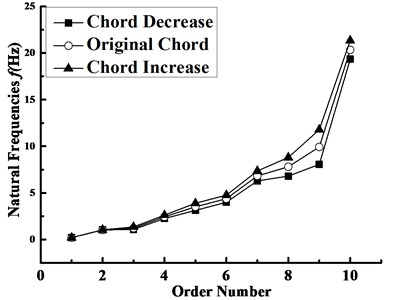
The design of the blade chord length is related to working efficiency, production cost, safety and many other aspects. Therefore, keeping GRP physical parameters constant, the chord length of each blade element group in Table 1 was increased or decreased 0.1 m, making the blade structure parameters change. For different chord lengths, the variation of the blade natural frequency with the order number is displayed in Fig. 11. With the chord length increasing equally, the increased amplitude of the natural frequency also reveals the same variation law with elasticity modulus, but there exists the other potential cause, that is, because the change of the blade chord length has a bigger effect on the stiffness than the mass, which results in the increase of the natural frequency. In addition, the chord length change has a more obvious impact on the shimmy and flapping frequencies of the first nine orders than the torsional one of the tenth order.
Fig. 10Natural frequencies of the blade with different mass densities
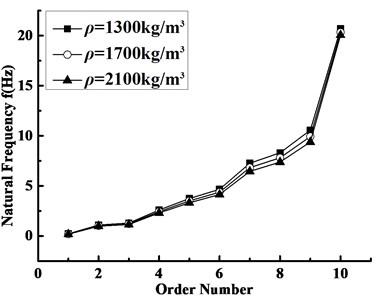
Fig. 11Natural frequencies of the blade with different chord lengths
6. Conclusions
In this work, the vibration modes of the 5MW wind turbine blade under different rotating speeds, material categories and manufacturing deviations of the material physical parameters and different chord lengths are numerically simulated and analyzed. The conclusions are summarized as follows:
1) With the increase of the rotating speed, the coupling effect of the rigid body motion and the deformation for the blade leads to the decrease of the natural frequencies from the first to the sixth order, while the centrifugal force results in the increase of the natural frequencies from the seventh to the tenth order. Hence, their combined effects should be considered under different working conditions and which factor plays a dominant role is ought to be analyzed. Only in this way can the vibration characteristic of the rotating blade be accurately reflected.
2) With the increase of the order number, the blade natural frequency basically presents a non-linear growth trend, and the changes of elasticity modulus, mass density and chord length make the difference value between the natural frequencies first increase, then decrease, and reach the peak value at the ninth order. Physical parameters and chord length have a greater impact on the shimmy and flapping frequencies of the first nine orders than the torsional one of the tenth order.
3) It is necessary to consider the influences of the dynamic stiffening effect and material manufacturing deviation simultaneously in the design of the natural frequency for wind turbine blades to avoid the structural instability phenomenon, which has a significant reference value to the blade safe operation.
References
-
Chen K., Song M. X., Zhang X. Binary-real coding genetic algorithm for wind turbine positioning in wind farm. Journal of Renewable and Sustainable Energy, Vol. 6, Issue 5, 2014, p. 053115.
-
Zhang J. P., Zhang K. G., Zhou A. X., Zhou T. J., Hu D. M., Ren J. X. Analysis of nonlinear dynamic response of wind turbine blade under fluid-structure interaction and turbulence effect. Journal of Engineering for Gas Turbines and Power Transactions of the ASME, Vol. 136, 2014, p. 1-5.
-
Kane T. R., Ryan R. R., Baneruee A. K. Dynamics of a cantilever beam attached to a moving base. Journal of Guidance, Control and Dynamic, Vol. 10, Issue 2, 1987, p. 139-151.
-
Wang Y. J., Pei P. Y. Finite element analysis for inherent mode of blade of wind turbine. Journal of Huazhong University of Science and Technology, Vol. 6, Issue 2, 2006, p. 44-46.
-
Gangele A., Ahmed S. Modal analysis of S809 wind turbine blade considering different geometrical and material parameters. Journal of the Institution of Engineers, Vol. 3, 2013, p. 225-228.
-
Tarfaoui M., Khadimalla H., Abdellatif I. A., Pradillon J. Y. Design and finite element modal analysis of 48 m composite wind turbine blades. Applied Mechanics and Materials, Vol. 146, 2011, p. 170-184.
-
Benham A., Thyagarajan K., John S. J., Prakash S. Structural analysis of a wind turbine blade. Advanced Materials Research, Vol. 768, 2013, p. 40-46.
-
Chen C., He B., Fu J., Fan Q. S. 3D Parametric modeling and vibration analysis of wind turbine blades. Machinery Design and Manufacture, Vol. 1, 2012, p. 57-59.
-
Wu C. M., Tian R., Chen Y. Y. Turbine blade design based on optimal vibration performance. Journal of Engineering Thermophysics, Vol. 29, Issue 11, 2008, p. 1857-1860.
-
Li D. Y., Ye Z. Q., Bao N. S., Chen Y. Vibration modal analysis of the rotating rotor of horizontal axis wind turbine. Acta Energiae Solaris Sinica, Vol. 25, Issue 1, 2004, p. 72-77.
-
Zhang J. P., Guo L., Wu H., Zhou A. X., Hu D. M, Ren J. X. The influence of wind shear on vibration of geometrically nonlinear wind turbine blade under fluid-structure interaction. Ocean Engineering, Vol. 84, 2014, p. 14-19.
-
Xin W. P. Analysis of Dynamic Characteristics and Response for Rotating Blades of Wind Turbine. Master’s Thesis, Department of Mechanical Engineering, Shantou University, China, 2005.
-
Jonkman J., Butterfield S., Musial W., Scott G. Definition of a 5-MW Reference Wind Turbine for Offshore System development. Technical Report, 2009.
-
Sun B. C., Li P. F. The simulation analysis of the bibration modal on a wind turbine blade under the stress stiffening effect. Renewable Energy Resources, Vol. 30, Issue 5, 2012, p. 38-41.
Cited by
About this article
The authors wish to acknowledge financial supports by various research funds including the National Natural Science Foundation of China (11572187); Innovation Program of Shanghai Municipal Education Commission (14ZZ154); Foundation of Science and Technology Commission of Shanghai Municipality (15110501000, 14DZ2261000).
Jianping Zhang established the theoretical and numerical model of the study. Fengfeng Shi achieved the numerical simulation. Jianping Zhang and Helen Wu carried out the analysis with constructive discussions and wrote the paper. Jianxing Ren, Hao Wang and Danmei Hu reviewed and edited the manuscript. All authors read and approved the manuscript.
