Abstract
Properties of nonlinear systems radically differ from linear in multivariance their behavior. In this regard, the control of such systems is a difficult task and has not been solved adequately problem of modern control theory. Methods of synergetic control theory (SCT) based on the idea of “nonload” impact on the system allow to create the objective control laws, which form the inner cooperative interactions between the processes of dynamic objects. The problem of the control of rotor supported by active magnetic bearings in artificial circulatory support device is presented in this paper. Because of strong nonlinear of the dynamical system the synergetic concept is apply for synthesis the effective control laws for the positioning of the pump rotor in the blood stream and provide the required parameters of the dynamics in terms of external disturbances to improve the efficiency of the artificial circulatory support device.
1. Introduction
Cardiovascular diseases (CVD) are one of the leading causes of death in the world according to the World Health Organization (WHO) [1]. The main alternative to heart transplantation today is artificial circulatory support device (ACSD) or left ventricular assist device (LVAD) [2, 3]. The ASCD helps the sore heart to pump blood from the left ventricle into the aorta. Models pumps are improved and some of them are successfully used in medical practice (Incor, HeartMate II, HeartWare, HeartMate III, Impella, etc.) [4]. One of the trends of development in this area is associated with the creation of axial blood pumps.
This approach let wait for a donor organ. Sometimes it is possible to restore the normal functioning of the heart, which is due to its partial discharge while wearing LVAD and further rehabilitation. But often patients continue to live with implanted pumps. Therefore, the main task of developing such devices is to improve the quality of the pump.
There are many problems by the development of ACSD. Some of them are blood trauma, thrombosis, the contact power system, unreliable of the devices [5]. The proposed in this article an axial blood pump has magnetic bearings as a rotor suspension. The magnetic bearings provide a noncontact rotor suspension and for the LVAD it is allow to reduce index of hemolysis, risk of platelet activation and thereby risk of thrombosis, to increase the durability and operational reliability of blood pump [6-7]. Moreover, there is no need for maintenance. In addition, the active magnetic bearings (AMB) are controlled by the electronic control scheme with feedback [7-9]. This allows to achieve higher accuracy of rotor positioning [8, 9].
Rotor stability in the magnetic field of the magnetic suspension depends on the control system which includes a controller. Controller is a logical device with an appropriate control law. So, the research object is the rotor supported by magnetic bearings in the blood flow. The rotor in magnetic field is an example of a nonlinear system. The properties of nonlinear systems radically differ from linear in multivariance their behavior [10]. In this regard, the control of such systems is a difficult task and has not been solved adequately problem of modern control theory [10].
SCT is a new approach to the control of the nonlinear dynamical systems. The main method of the SCT is Analytical Design of Aggregated Regulators (ADAR), which is based on the idea of introduction to the phase space of dynamical system attracting invariant manifolds, on which natural (energetic, mechanical, technological, etc.) properties of the control object and requirements of control task in the best way are coordinated. The principle of integrated adaptation of ADAR method ensures the required dynamic characteristics of the system under the action of external disturbances. Unlike similar approach the SCT allows to optimize the behavior of systems not only in the nominal modes and areas of “big” and “small” deviations from them, but to consider qualitatively different modes of behavior of nonlinear dynamical systems such as bifurcations and phase transitions, undesirable and dangerous attractors in their state space, non-uniqueness of the solution of control task, etc. [10-13]. Methods of synergetic control theory based on the idea of “nonload” impact on the system, is not contrary to the natural movement of the object, allow to create of objective control laws, which form the inner cooperative interactions between the processes of dynamic objects [10].
As it was told above corresponding to the ADAR method the attracting invariant manifolds are entered into the phase space of the dynamical system. The requirements of control task are performed when system representative point falls on these attracting invariant manifolds. Control laws, which transform the representative point for these manifolds are found in the synergetic synthesis [10-13]. The purpose of this work is to synthesize the synergetic control laws for the positioning of the pump rotor in the blood stream and to provide the required parameters of the dynamics in terms of external disturbances to improve the efficiency of the artificial circulatory support device.
2. Task formulation
The rigid rotor rotates with the constant angular velocity . The nonlinear system describing the dynamics of rotor supported by two radial AMB in matrix form is following [8, 9]:
where is the vector of generalized coordinates, is the inertia matrix, is the gyroscopic matrix, is the damping matrix due to motor, and are matrices, which present hydrodynamic phenomenon due to motion in liquid, is the transformation matrix, is the stiffness matrix, taking into account the effect of the motor, is the vector of magnetic forces, is the vector of external disturbances, is the unbalances matrix, – vector of and , is the vector with gravity as component. Movement of the rotor in the axial direction is not considered.
The relationships between the magnetic forces acting on the rotor by two radial active magnetic bearings A and B and coil currents, and the displacements of the rotor have the nonlinear form [9]:
Here and are structural parameters of AMB, is the bias current, , , , are control current corresponding to the direction and AMB, is the gap. The vector comprises the rotor displacements within the magnetic bearings.
Control task is positioning the rotor axis with prescribed accuracy. The gap in proposed blood pump is 0.2 mm and a maximal shift or distortion of the rotor axis should not exceed a linear size = 0.1 mm.
There are piecewise constant and harmonic external disturbances of inertial nature to which the rotor is exposed:
Here , , , are projections of the external disturbance piecewise constant character, , , , are projections of the amplitude of the external harmonic disturbance, is the frequency of the external harmonic disturbance. Moreover, unbalances play a role of an external oscillatory excitation and contribute to the emergence of additional vibrations.
In this way the control tasks could be formulate as follows:
1) Centering the rotor axis with the requirement accuracy;
2) Suppression of external disturbances piecewise constant and harmonic characters with previously unknown amplitude;
3) Global stability of the system.
The synthesis of control laws by ADAR method with the principle of integrated adaptation of synergetic control theory is presented in the next section.
3. Synergetic synthesis
According to the synergetic control concept [10-13] the control tasks have to be presented in form of invariants. In our case the technological invariants have the following form:
where , , , are state coordinates in Cauchy normal form, , , , are desired values of state coordinates equal to zero.
For the suppression of external disturbances, it is necessary to present each of them as a dynamic model, which is formed approximated impact of the relevant class at the output. Such approach is called the principle of integrated adaptation.
The “Model of synergetic synthesis” is obtained:
Here are constant coefficients, related to the parameters of rotor and AMBs, are renaming for convenience, are coordinates of the expanded subsystem (external excitations), , , , are constant coefficients, , , , are control channels (control coil currents).
It is necessary to find such a control vector , which provides translation of the object Eq. (5) from an initial state to the predetermined state, characterized by a set of invariants Eq. (4). According to the number of control channels a parallel set of macrovariables (invariant manifolds), containing technological invariants, is introduced [10-13]:
where , , , are constant coefficients.
To find control laws we must solve a system of general functional equations of ADAR method:
where are time constants, influencing to the dynamics.
Control actions , , , could be found at the simultaneous solution of the Eqs. (4-7).
4. Results: dynamic analysis
The rotor behavior in magnetic field under external disturbances with synthesized synergetic controller is presented in this section. Fig. 1 shows the transients of state variables , , , of closed-loop system Eq. (5) with synergetic controls. The parameters of synergetic control laws are the following: , , , , , , 1,…,4, , . The initial conditions for the system state variables are zero except , , , .
The modeling results demonstrate the centering of rotor axis with the required accuracy and the suppression of external disturbances as the piecewise constant and harmonic character due to inertial nature and unbalances. The state variables are invariant to changes in external factors and the control laws ensure asymptotically stable character of transients. The fast transients and the lack of oscillation are provided in the dynamical closed-loop system. It is important to note that the synergetic control laws perform the specified technological tasks.
From simulation results we can see the influence of control parameters on the accuracy of rotor positioning and the oscillation of dynamic process. First of all, the influence to the dynamics of the first constant parameters in Eq. (6) , , , was investigated. As a matter of convenience the transients of state variable are presented in Fig. 2. It is visible that the accuracy of rotor axis and the oscillation of dynamic process depend on this parameter. Here and further the simulation is carried out for the same rotor and AMBs parameters and the values of the other parameters are the same as above. With solid bold line the variant that satisfies the requirements of precision is marked.
On the example of transients of the influence of the control parameters, , , is presented in Fig. 3. With solid bold line the value of that satisfies the requirements of precision is marked.
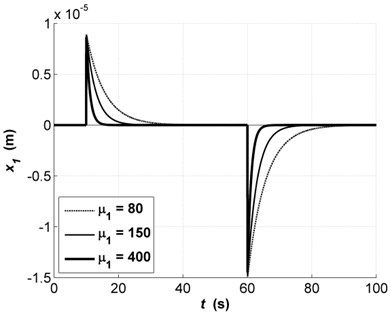
The modeling results with changes in parameters , (Eq. (5)) are presented in Fig. 4 on the example of transients of .
As shown in Fig. 4 the transient rate depends on , . With solid bold line the value of that satisfies the requirements of precision is marked.
Fig. 1Transients of state variables
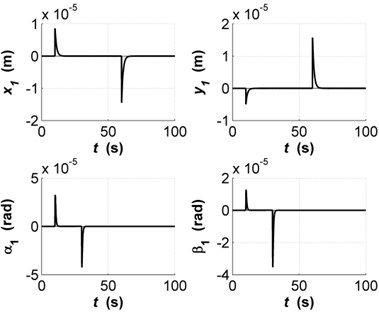
Fig. 2Transients of α1 with changes in parameter ρ31: ρ31=1 (dashed line), ρ31=3 (solid thin line), ρ31=10 (solid bold line)
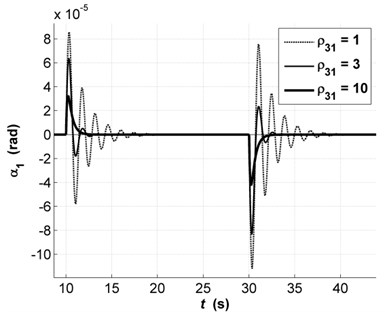
Fig. 3Transients of x1 with changes in parameter ρ12: ρ12=150 (dashed line), ρ12=40 (solid thin line), ρ12=0.1 (solid bold)
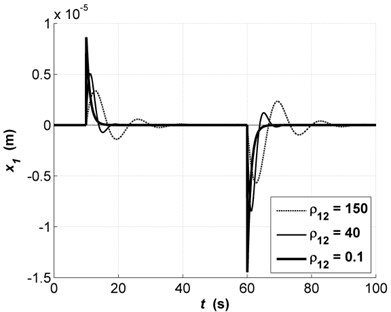
Fig. 4Transients of x1 with changes in parameter μ1: μ1=80 (dashed line), μ1 =150 (solid thin line), μ1 =400 (solid bold line)
5. Conclusions
The synergetic control theory, based on the idea of introduction of invariants manifolds, is the new approach to the control of nonlinear, multidimensional, multiply connected dynamical systems, which allows to synthesize the effective control laws, providing the required parameters of the dynamics in terms of external disturbances. This opens up the new possibilities in the direction of the development of control of the rotor supported by magnetic bearings in artificial circulatory support device.
References
-
10 Leading Cause of Death in the World. World Health Organization, www.who.int/mediacentre/factsheets/fs310/ru/index2.html, 2016, (in Russian).
-
DeBakey M. E. A miniature implantable axial flow ventricular assist device. 4th International Conference on Circulatory Support Devices for Severe Cardiac Failure, Houston, TX, 1997, p. 637-640.
-
Reul H. M., Akdis M. Blood pumps for circulatory support. Perfusion, Vol. 15, Issue 4, 2000, p. 295-311.
-
Bogdanova Yu. V., Guskov A. M. Left Ventricular Assist Device (LVAD) Design Features: Literature Review. Science and Education, http://technomag.bmstu.ru/en/doc/705250.html, 2014.
-
Finocchiaro T., et. al. Methods of design, simulation, and control for the development of new VAD/TAH concepts. Biomed Technologies, Vol. 54, Issue 5, 2009, p. 269-281.
-
Antunes P., et. al. Magnetic suspension of the rotor of a ventricular assistance device of mixed flow type hall sensor for rotor position measurement use of compensator. ABCM Symposium Series in Mechatronics, Rio de Janeiro, Brazil, 2012, p. 1249-1256.
-
Greatrex N. A. Design of Physiological Control and Magnetic Levitation Systems for Total Artificial Heart. Ph.D. Dissertation, B.Eng., B.Math., Queensland University of Technology, Australia, 2013.
-
Schweizer G., Maslen E. Magnetic Bearings. Theory, Design and Application to Rotating Machinery. Springer-Verlag, Berlin, German, 2009.
-
Zhuravlev Juri N. Active Magnetic Bearings: Theory, Design, Applications. Politehnica, St. Petersburg, Russia, 2003, (in Russian).
-
Kolesnikov A. A., et. al. Modern Applied Control Theory: Synergetic Approach in Control Theory. TSURE Press, Taganrog, Russia, 2000, (in Russian).
-
Kolesnikov A. A., et. al. Synergetic Control Methods of Complex Systems: Mechanical and Electromechanical Systems. URSS, Moscow, Russia, 2013, (in Russian).
-
Kolesnikov A. A., et. al. Synergetic Control Methods of Complex Systems: Energy Systems. URSS, Moscow, Russia, 2013, (in Russian).
-
Kolesnikov A. A. Synergetic Control Theory. Energoatomizdat, Moscow-Taganrog, Russia, 1994, (in Russian).
About this article
The research was supported by the Russian Foundation for Basic Research (Grant No. 15-29-01085 ofi_m).
