Abstract
A novel numerical predictive approach for steady-state response of thin orthotropic plate is presented based on wave-based method (WBM) that is applied in bending vibration prediction of thin and thick plate in mid-frequency range. The wavenumber parameters for orthotropic material and the particular solution of an infinite orthotropic plate with Fourier transform are derived. The proposed method is validated by numerical examples with simply supported boundary and clamped boundary. The compared result shows that the computational accuracy and efficiency of WBM is significantly higher than element based method, which is the ability of WBM for mid-frequency problems. The predictive ability of WBM is extended to process the dynamic response of orthotropic plate.
1. Introduction
With the improvement of material technology and increase of demand for structure performance, more and more composite materials like honeycomb panels and fibre reinforced polymers are adopted to lower weight of the products in aerospace and automotive industry. Among which, thin orthotropic plate is the typical structure used in such transport production, and the bending vibration behavior of this class structure is the key factor to influence NVH performance of product. Thus, the response of orthotropic plate has been talked about by analytical or semi-analytical methods [1-4]. With the requirement of lowering the cost of time and computation, the CAE techniques based on numerical method is indispensable for engineers to predict the deterministic bending vibration response of such composite structure, especially in design and optimization process.
Currently, the element based methods like Finite Element Method (FEM) [5] and Boundary Element Method (BEM) [6] are proverbially applied for vibration and acoustic prediction. They divide the problem domain into finite elements, in which the variables are approximated by a set of simple polynomial functions that is not exactly satisfy the physical governing equation and boundary conditions, which results interpolation error and pollution error [7]. For higher frequency problems, the element size need to be small enough to capture the property of short wavelength, which sharply increasing the computational cost and time. Therefore, the element based methods usually used in low frequency issues. On the other hand, the Statistical Energy Analysis (SEA) [8] divides the system into finite subsystem, and the dynamical response of system is calculated through the balance and exchange of different subsystems. However, such statistical method is merely available for higher frequency problems under the theoretical hypothesis that each subsystem has high modal density during concerning frequency range. In the frequency range between the low and high frequency, called mid-frequency, system contains long wavelength and short wavelength characteristic, so a high efficiency and high robustness numerical method is necessary for predicting the vibration feature of structure.
Over the recent years, a variety of techniques have been proposed to deal with the mid-frequency problems. And the first idea is extending the frequency range of present methods, such the Galerkin least-squares FEM [9], the quasi-stabilized FEM [10], Statistical energy analysis energy method [11], Energy-density field approach [12], Hybrid SE-FEM [13]. the other family of solution algorithms is based on Trefftz method [14] which describes the field variables with a combinations of basis functions that satisfy the governing equation. Such approaches include the ultra-weak variational method [15], the wave boundary element method [16], The variational theory of complex rays [17]. The Wave Based Method(WBM) which is addressed in this paper is belongs to this family of solutions.
In the end of 20 centuries, W. Desmet proposed a novel numerical technique for mid-frequency vibro-acoustic problems [18], its advantages of high accuracy and convergence is revealed. Then WBM is widely applied for prediction of sound and vibration areas. For example, vibration of thin and thick plate [19, 20], analysis of vibro-acoustic radiation problems [21], modelling of Poroelastic Materials [22]. In order to break through the application limitation that WBM is only convergence in convex domain, many extending techniques are present, like multi-level wave based technique [23], Hybrid FEM-WBM [24], Hybrid BEM-WBM [25]. Therefore, the extending of this techniques is significant for engineering application.
This study aims to propose a novel efficient numerical approach based on the theory of wave based method and the orthotropic plate. This paper is organized as follow. The vibration theory of orthotropic plate is reviewed in Section 2. The basic formulation of WBM for orthotropic plate is derived, and the particular solution of orthotropic plate resulted by concentrated force is obtained through Fourier transform in Section 3. The numerical examples are presented and the methodology is validated in Section 4. Finally, the conclusions are drawn in Section 5.
2. Vibration of orthotropic plate
For plate vibration analysis, there are two main theories: The Kirchhoff and the Resissner Mindlin theory. Kirchhoff theory assumes that the shear deformation of plate is zero, or that the normal of the middle plane remain normal during deformation. The Kirchhoff assumption remains valid as long as the bending wavelength is approximately six times larger than the plate thickness. In view of the objective is thin plate, Kirchhoff theory is adopted for describing the vibration feature of orthotropic plate. For a thin orthotropic plate, when , axis parallel to the elastic principal direction, its transversal displacement is governed by the orthotropic Kirchhoff equation under external excitation [1]:
where orthotropic plate parameters are given as:
with Young’s modulus , and Poisson’s ratios , in the directions of the coordinate axes and respectively, the shear modulus in plane. the plate material density and the plate thickness.
For a time harmonic load with circular frequency , the steady-state response of orthotropic plate changed as:
To solve the fourth-order equation and acquire the out-of-plate displacement , two structural boundary conditions are required. The common boundary conditions at plate edges are defined as follow:
Dynamical boundary:
Mechanical boundary:
Mix boundary:
With , , and the boundary value for respectively, the displacement, the rotational displacement, the bending moment and the equivalent shear force. , , the differential operators for rotational displacement, bending moment, and the equivalent shear force. The corresponding variables in orthotropic material are defined as follow:
Rotational displacement:
Bending moment:
Equivalent shear force:
3. Wave based method
Wave based method that belongs to indirect Treffz method is a deterministic numerical technique, in which the field variables are expressed as a combination of set of wave functions that satisfy the governing equation exactly. On the use of weighted residual formulation, the boundary errors are enforced to zeros and the contribution factors of wave functions are determined. Subsequently, the approximation of out-of-plate displacement is obtained.
3.1. Field variable expansion
On the basic methodology of wave based method, the dynamic response of plate is approximated by the serials of wave functions :
Where is the structure wave functions that satisfy the homogeneous governing equation, is the contribution factors of wave functions. represents the particular solution resulted by external load, which will be discussed in the next section.
For isotropic plate, Desmet proposed the set of wave function defined as follow [19]:
is defined the degree of model which decides the computational cost. Substituting set of wave functions in Eq. (10) into the homogeneous governing equation of orthotropic plate as Eq. (2), yields the equations containing wavenumber parameters for orthotropic plate:
Similarly, the is the structural wave number. Combining the above equations, the new wavenumber parameters for orthotropic material is derived:
With , the outside dimension of plate in the direction of and respectively.
The type of solution in Eq. (9) converges towards the exact solution for infinite number of wave functions, so a truncation of wave functions is required for practical implementation. The adopted truncation rule is frequency dependent and links the wavenumber of the highest oscillating wave function to the physical wavenumber of the considered problem. This infinite series is truncated by selecting a value for the truncation parameter , which satisfies follow rule:
3.2. Particular solution
in Eq. (9), which is the particular solution of Eq. (2), denotes the dynamic response of infinite plate by external load. In this paper, a concentrated point force in consider. For a time harmonic point force in the -direction at , the load expressed as:
So, the Eq. (2) changed as:
Transforming into wavenumber domain by Fourier Transform, the displacement response is expressed as:
So, the Eq. (17) is transformed in the same way and the integration variables are changed from to with And the rectangular coordinate is transformed into cylindrical coordinate by , . Integrating Eq. (20) form to , yields the approximation of particular solution for an infinite orthotropic plate [26]:
where:
To reveal the feature of particular solution for orthotropic plate, the displacement of a square Graphite–epoxy plate with size (0.2 m×0.2 m) that is excited by a unit force in the center is calculated with the proposed approach. The material parameters of plate including: fiber angle = 0, 138 GPa, 8.9 GPa, 5.176 GPa, 0.3, 1600 kg/m3, 0.005 m. The result shown in Fig. 1 is the real part and imaginary part of displacement of the orthotropic plate respectively. Comparing with isotropic plate, the propagation of wave is no longer axisymmetric but varies with the modulus of each principal direction.
Fig. 1Displacement response of an infinite orthotropic plate
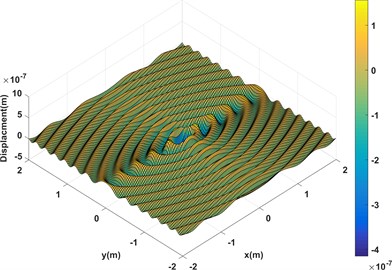
a) Real part
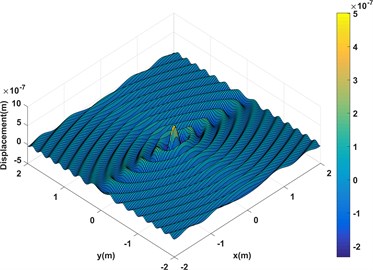
b) Imaginary part
3.3. Boundary weighted residual formulation
The field variables are approximated by exact wave functions, so the errors of WBM are barely generated on boundary. Therefore, the contribution factor of each wave function is obtained through enforce the boundary errors to be zeros. To minimize the errors, Galerkin method that belongs to weighted residual method is adopted:
where is the weighted function which is the set of structure wave functions.
Substituting the boundary residual , , , into Eq. (23), yields the ill-conditioning system matrix containing contribution factors . Solving Eq. (24), the dynamic displacement response of orthotropic plate is acquired:
where:
4. Numerical validation and discussion
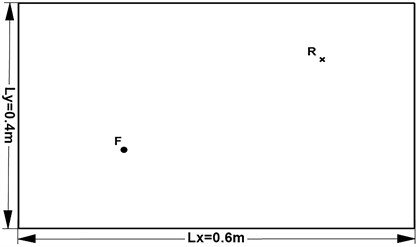
To validate the proposed methodology, a rectangular orthotropic plate is introduced. The problem geometry is depicted in Fig. 2 and is same for all the case. The plate is made of a unidirectional fibre reinforced polymer whose material parameters is presented in Table 1. The plate has a thickness of 0.001 m and a unit normal force is applied at (0.16 m, 0.14 m). A response point that is selected for surveying its frequency response located at (0.46 m, 0.3 m). The simply supported and clamped boundary condition will be considered. And there are two key points to be validated: the one is the accuracy which is illustrated in Section 4.1 and 4.2, another is the efficiency that is specified in Section 4.3.
Table 1Mechanical properties of orthotropic materials.
120 GPa | 10 GPa | 0.3 | 4.9 GPa | 1510 kg/m3 |
WBM is implemented in MATLAB with truncation coefficient 6. With the purpose of validation of WBM for predicting the bending vibration of orthotropic plate, WBM predictions are compared with those obtained by FEM. FEM is realized by MSC/Nastran2012 in this study. In order to ensure the accuracy of calculation, FE model is fine meshed with eight-node quadrilateral shell element and is consisted of degrees of freedom 45501. All FE models are solved by using the direct solution method.
Fig. 2Problem geometry
4.1. Simply supported plate
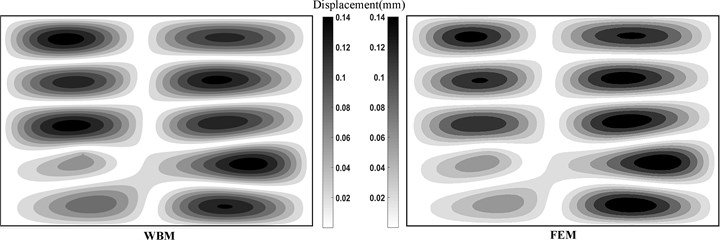
In this validation example, all the boundaries of orthotropic plate are simply supported. Fig. 3 shows the compared contour of displacement with both WBM and FEM at 200 Hz. The displacement response obtained by WBM is considerable agree with those obtained by FEM.
Fig. 3Displacement of orthotropic plate with simply supported boundary at 200 Hz
In consideration of four simply supported boundary, the doubly infinite series type of solution for such orthotropic plate is available [27]. So, the series solution is introduced to demonstrate the validity of WBM:
where:
with , , , , is the wave number of half-sinusoid in , direction separately, and 50 in this study.
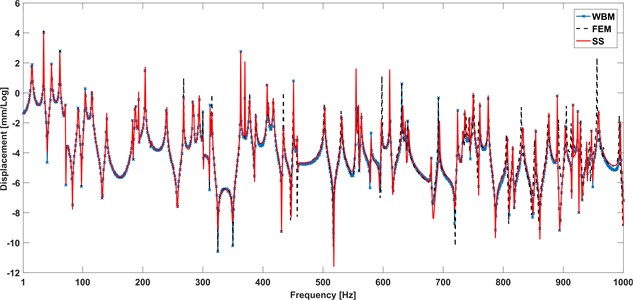
Fig. 6 shows the predictive displacement response of selected point within 1-1000 Hz. in order to reflect the nuance of three plot obtained by different approaches, the compared results are presented in the form of logarithm. Form the plots, the results by using the WBM based approach is in good agreement with the results calculated by FEM and series method, which verifies that WBM is applied to predict the bending vibration of orthotropic plate with simply supported edges.
Fig. 4Frequency response of response point R with simply supported boundary
4.2. Clamped plate
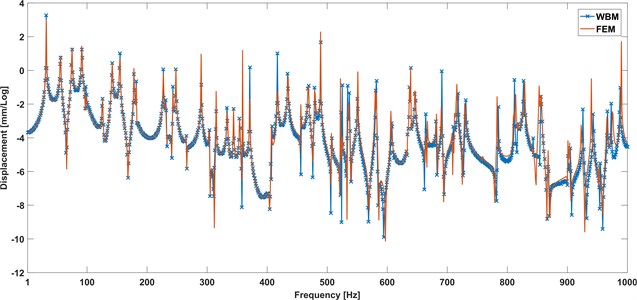
In this section, the example with all boundaries clamped is discussed. Similar to the Section 4.1, this section is to validate the accuracy of WBM for orthotropic plate with clamped boundary. The displacement contours at 150 Hz predicted by WBM and FEM are depicted in Fig. 5, in which we can see the predictions with WBM are fit well with the FEM analysis. Additionally, the logarithmic frequency responses of selected point in 1-1000 Hz shown in Fig. 6 similarly certifies that the proposed approach based on WBM is available for predicting the bending vibration of orthotropic plate precisely.
Fig. 5Displacement of orthotropic plate with clamped boundary at 150 Hz

Fig. 6Frequency response of response point R with clamped boundary
4.3. Convergence
As mentioned above, the aim of numerical examples is to validate the method in both accuracy and efficiency. And the proposed approach based on WBM is validated that this method is precisely available for prediction of translational displacement of thin orthotropic plate. Then, the efficiency of WBM is illustrated in this section via the convergence analysis.
The accuracy of WBM and FEM are ensured by number of truncation parameters and by the number of element respectively. And the number of wave function in WBM and number of node in FEM is the decision of computational cost and corresponding computing precision. To find the computational efficiency of WBM, the relative prediction error defined in Eq. (29) is introduced. The convergence analysis of numerical predictive technique is to find out the relation between predictive precision and the computational cost. The predictive displacement amplitudes of point with two boundaries at 500 Hz are selected as the objectives for convergence analysis in this study:
With the referenced prediction obtained by fine meshed FE model.
Fig. 7 presents the convergence curves containing relative error and degree of freedom of both WBM and FEM. The compared result shows that the convergence rate of WBM is dramatically higher than FEM, which validates the higher computational efficiency of WBM. At this point, WBM is more available for mid-frequency problems contrasted with element based method.
Fig. 7Comparison of the convergence of FEM and WBM
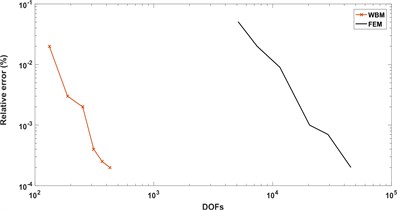
a) Simply supported boundary
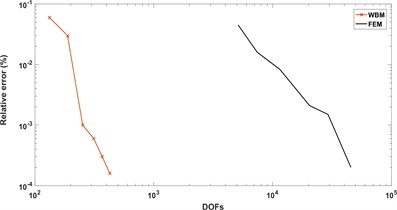
b) Clamped boundary
5. Conclusions
A novel prediction technique based on WBM for steady-state response of orthotropic plate is proposed. The new wavenumber parameters of wave function are derived and the particular solution for infinite orthotropic plate is introduced. The methodology of presented approach is validated by numerical examples with different boundary conditions. The outstanding computational accuracy and efficiency of WBM is verified by the comparison with FEM. And the vibro-acoustic prediction of complex geometry with orthotropic material based on wave based technique is to be studied on next stage.
References
-
Lekhnitskii S. Anisotropic Plates. Gordon and Breach ,1968.
-
Papkov S. О. Steady-state forced vibrations of a rectangular orthotropic plate. Journal of Mathematical Sciences, Vol. 192, Issue 6, 2013, p. 691-702.
-
Rahbar Ranji A., Rostami Hoseynabadi H. A semi-analytical solution for forced vibrations response of rectangular orthotropic plates with various boundary conditions. Journal of Mechanical Science and Technology, Vol. 24, Issue 1, 2010, p. 357-364.
-
Ahmadian M. T., Sherafati Zangeneh M. Vibration analysis of orthotropic rectangular plates using superelements. Computer Methods in Applied Mechanics and Engineering, Vol. 191, Issues 19-20, 2002, p. 2097-2103.
-
Zienkiewicz O. C., Taylor R., Zhu J. The Finite Element Method: Its Basis and Fundamentals, Sixth Ed. Butterworth-Heinemann, 2005.
-
Von Estorff O. Boundary Elements in Acoustics: Advances and Applications. WIT Press, 2000.
-
Bouillard P., Ihlenburg F. Error estimation and adaptivity for the finite element method in acoustics: 2D and 3D applications. Computer Methods in Applied Mechanics and Engineering, Vol. 176, Issues 1-4, 1999, p. 147-163.
-
Lyon R., DejJong R. Theory and Application of Statistical Energy Analysis, Second Ed. Butterworth-Heinemann, 1995.
-
Harari I., Hughes T. J. R. Galerkin/least-squares finite element methods for the reduced wave equation with non-reflecting boundary conditions in unbounded domains. Computer Methods in Applied Mechanics and Engineering, Vol. 98, Issue 3, 1992, p. 411-454.
-
Babuska I., Ihlenburg F., Paik E. T., Sauter S. A. A generalized finite element method for solving the Helmholtz equation in two dimensions with minimal pollution. Computer Methods in Applied Mechanics and Engineering, Vol. 128, Issues 3-4, 1995, p. 325-359.
-
Mace B. Statistical energy analysis energy distribution models and system modes. Journal of Sound Vibration, Vol. 264, Issue 2, 2003, p. 391-409.
-
Kassem M., Soize C., Gagliardini L. Energy-density field approach for low- and medium-frequency vibroacoustic analysis of complex structures using a statistical computational model. Journal of Sound Vibration, Vol. 323, Issues 3-5, 2009, p. 849-863.
-
Langley R. S., Bremner P. A hybrid method for the vibration analysis of complex structural-acoustic systems. Journal of The Acoustical Society of America, Vol. 105, Issue 3, 1999, p. 1657-1671.
-
Trefftz E. Ein gegenstuck zum ritzschen verfahren. Second International Congress on Applied Mechanics, 1926.
-
Cessenat O., Despres B. Application of an ultra-weak variational formulation of elliptic PDEs to the two-dimensional Helmholtz problem. Siam Journal on Numerical Analysis, Vol. 35, Issue 1, 1998, p. 255-299.
-
Perrey-Debain E., Trevelyan J., Bettess P. Wave boundary elements: A theoretical overview presenting applications in scattering of short waves. Engineering Analysis with Boundary Elements, Vol. 28, Issue 2, 2004, p. 131-141.
-
Ladeveze P., Arnaud L., Rouch P., Blanze C. The variational theory of complex rays for the calculation of medium-frequency vibrations. Engineering with Computers, Vol. 18, Issues 1-2, 2001, p. 193-214.
-
Desmet W. A Wave Based Prediction Technique for Coupled Vibro-Acoustic Analysis. Ph.D. Dissertation, Katholieke Universiteit Leuven, 1998.
-
Vanmaele C., Vandepitte D., Desmet W. An efficient wave based prediction technique for plate bending vibrations. Computer Methods in Applied Mechanics and Engineering, Vol. 196, Issues 33-34, 2007, p. 3178-3189.
-
Klanner M., Ellermann K. Wave Based Method for the steady-state vibrations of thick plates. Journal of Sound and Vibration, Vol. 345, 2015, p. 146-161.
-
Bergen Bart, Pluymers Bert, Van Genechten Bert, Vandepitte Dirk, Desmet Wim A Trefftz based method for solving Helmholtz problems in semi-infinite domains. Engineering Analysis with Boundary Elements, Vol. 36, Issue 1, 2012, p. 30-38.
-
Deckers Elke, Jonckheere Stijn, Vandepitte Dirk, Desmet Wim. Modelling techniques for vibro-acoustic dynamics of poroelastic materials. Archives of Computational Methods in Engineering, Vol. 22, 22015, p. 183-236.
-
Van Genechten B., Vergote K., Vandepitte D., Desmet W. A multi-level wave based numerical modelling framework for the steady-state dynamic analysis of bounded Helmholtz problems with multiple inclusions. Computer Methods in Applied Mechanics and Engineering, Vol. 199, Issues 29-32, 2010, p. 1881-1905.
-
Van Genechten B., Vandepitte D., Desmet W. A direct hybrid finite element – wave based modelling technique for efficient coupled vibro-acoustic analysis. Computer Methods in Applied Mechanics and Engineering, Vol. 200, Issues 5-8, 2011, p. 742-764.
-
Santana A., Aznárez J. J., Padrón L. A., Maeso O. A BEM–FEM model for the dynamic analysis of building structures founded on viscoelastic or poroelastic soils. Bulletin of Earthquake Engineering, Vol. 14, Issue 1, 2016, p. 115-138.
-
Magliula Elizabeth A. Far-field approximation for a point-excited anisotropic plate. Journal of The Acoustical Society of America, Vol. 131, Issue 6, 2012, p. 4534-4542.
-
Jiang Weikang, Zhu Jimei Boundary element method for dynamic response of orthotropic plate. Journal of Vibration Engineering, Vol. 1, Issue 2, 1988, p. 55-62.
Cited by
About this article
The research work of authors is funded by Chongqing Foundation and Advanced Research Project (Grant No. CSTC2015jcyjBX0075) and Fundamental Research Funds for The Central Universities (Grant No. 106112016CDJZR335522).
