Abstract
In this study new numerical models were developed and applied to the analysis of the performance of precision optical encoder operating in non-ideal environments. Numerical simulation and experimental examination of imperfections in the generated waves were carried out to examine the influence of various factors affecting the encoder accuracy.
1. Introduction
Linear and angular optical encoders are precision measuring instruments often used in high precision machines for position detection and motion control. The accuracy and performance of the encoder is mostly influenced by the instrumental errors inherited in the manufacturing and assembly process (e.g. graduation errors, eccentricity) and external factors like temperature deviations, vibration, etc. Therefore, comprehensive analysis and quantitative estimation of such error sources are necessary for improvement of resolution and accuracy of such encoders as well as for optimization of encoder structures.
The resolution of an optical incremental encoder is mainly determined by the quality of the interfering periodic structures – the scale which implements the function of measuring standard and scanning reticle used to generate a particular form of the output signal. The form and precision of output signals depend on the scheme of the interaction of both structures. As a result of the superposition of two straight line grating structures an interference pattern (Moiré fringes) can be observed. The position, pitch and form of combinative interference lines are determined by the mutual position and the parameters of the two gratings. The grating combination performs the scaling function by transforming the small measured displacements to much larger proportional displacements of Moiré fringes.
In general, classical geometric and spectral approach can be used for investigation of the Moiré phenomenon [1-6]. Spectral (Fourier) approach based on the duality of functions in time or space domain and their spectra in the frequency domain related by the Fourier transform may solve numerous grating interaction problems and enables us to analyze the signals produced by interfering gratings and their superposition as well as the corresponding spectra. Application of Fourier analysis methods and selection of different combinations of gratings’ parameters permits particular simulation of required light transmission (modulation) properties of an optical encoder. However, possibilities of the analytical and spectral methods are limited if aperiodic or random grating structures (which are inevitable due to instrumental errors of the encoders) are to be investigated [5-6]. For the analysis of such non-repetitive or random structures numerical (binary) models are much more practical and effective tool as they enable not only direct and ostensive evaluation of the superposition images of the structures but also implication of other error sources like geometrical, dynamic or thermal errors in the numerical model.
2. Moiré effect in optical encoders
The Moiré images appearing due to the superposition of non-periodic or random structures are referred to as Glass images. Differently from Moiré pattern of periodic structures which overlay the whole interacting structure, the Glass patterns are concentrated around a certain superposition point of superposition and are fading out as the distance from the point is increasing. Though formally the Fourier techniques can be applied for the analysis of Glass images, they often appear as of no particular efficiency in practical applications [4, 5].
Optical encoders based on moiré effect with traditional coarse gratings (diffraction effects can be ignored) may be modelled by transmittance (or reflectance) functions of these gratings [1-2, 7]. Monochromatic image as well as the grating structure can be represented in the image domain by a transmittance function at any point (, ) obtaining values in the range between 0 and 1, which correspond to opaque and transparent lines respectively. The result of the combination of the “black” and any other shade is the “black” value which validates the multiplicative model for monochromatic images. The superposition of monochromatic images provides the resultant image as the product of transmittance functions of individual images or grating structures; ; ,…, . The Fourier transform of the product of functions is obtained as the convolution:
of Fourier transforms ; 1,…, of individual functions ; ; ,…, where , are the spectral plane parameters.
In the optical encoders the transmittance function characterizes the changes of the light flux passed through the interfering gratings as:
where is the light flux passed through the grating combination, is the light flux of the incident on the scanning grating (window), is the irradiance created by the incident light, is the area of the scanning window.
The general analytical case of the light signal generated by interaction of two graduations, where the scanning grating moves in the direction, can be expressed as [8]:
where is the number of transparent sectors of scanning grating within the considered range, – the distance between the centres of adjacent transparent sectors of the scanning grating, – height of transparent sectors (equal to the height of the window of the analyzing diaphragm, ; – spatial frequencies, and – periods of spatial harmonic components along and axes correspondingly, – integer number of a harmonic component, – initial displacement of the scanning grating in direction (usually ), , , – pitches of interacting grating structures, – the width of the transparent sector of the grating, – inclination angle if the scanning grating respectively to axis, – inclination angle of the end of line of the scanning grating with respect to the analyzing diaphragm (usually 0), – inclination angle of the centre lines of the scanning grating with respect to axis.
The obtained limit values of the transmittance function may be used for determining the depth of modulation m of the combination of both graduations as:
Thus using the methods of Fourier analysis and selecting proper parameters of grating and analyzing diaphragm a desired transmittance function of the grating combination, as well as, the depth of modulation can be obtained.
Such methods are suitable for determining the properties of regular grating structures. However, for the analysis of non-regular and random grating structures (with which is necessary to deal with during investigations of the influence of the transducer errors on generated measurement signals) the methods based on Fourier analysis has limited performance. They enable the direct visual and mathematical analysis of images of grating superposition.
2.1. Light modulation by interfering gratings
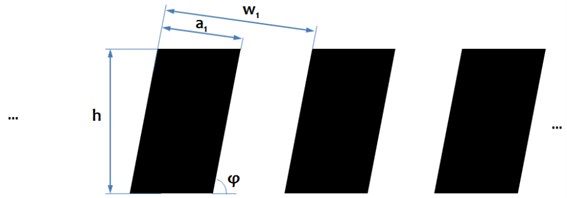
The numerical simulation model of light modulation is based on the direct binary representation of the grating geometry by a binary matrix (BM) where opaque and transparent lines are represented as “0” and “1” values as shown Fig. 1. The location of ones and zeroes in the matrix is in one-to-one correspondence with the geometrical view of the graduation lines. Each position in a row of the matrix represents the distance in the horizontal direction, and each row of the matrix represents the distance in the vertical direction.
Fig. 1Numerical models of vertical a) and oblique grating lines b) represented by binary arrays and their main characteristics
a)

b)
The discretion of “dark” and “transparent” junction lines depends on the number of bits in BM designed for representation of a unit of length. The position errors in the horizontal (width) and vertical (height) directions can be obtained as:
Each graduation is characterized by their light flux transmittance. It is assumed that the opaque lines are completely lightproof and the bright lines are ideally transparent for the light flux. Then the transmittance function of a grating can be calculated as:
where is the inclination angle of the graduation lines against the horizontal line as shown Fig. 1.
In the simulation model the interaction of two interfering gratings is presented as the logical sum of the two BM representing a combined result as:
The combined transmittance of a certain interaction of two graduations is obtained as a ratio of the number of “ones” elements over the total number of the elements in the BM representing the interaction matrix Eq. (7) of graduations as:
There are several common schemes of gratings’ interaction:
• Interaction of gratings with vertical lines and referred further as an obturative interaction. It can be regarded as a marginal case of the general moiré pattern applied in optical incremental encoders.
• Interference of gratings at 0 where inclined moiré fringes are generated, as shown Fig. 1.
It is important to note that Eq. (8) remains valid for any value of and which determine the distance corresponding to one binary position in the BM in horizontal and vertical directions.
The BM representation of the grating is obtained directly from the graphical images of the grating micro-geometry represented on the computer monitor as enlarged many times. Thus graduation errors and deviations of the positions of graduation lines caused by external factors (e.g. temperature deformations and/or vibrational displacements) can be introduced by entering zeroes and ones at the appropriate positions into BM [9, 10]. Position or inclination angle deviations, non-uniformity of graduations’ width, changes of the measuring point position in time due to structural vibrations, etc. are represented by plotting the profile of the grating on the screen and filling the obtained areas with a color. The interaction of both gratings is modeled by superimposing two graduation structures one upon another in the same image. In case the images are black-white, the interference pattern of both gratings [5] is simulated using the graphical processing capabilities of the computer monitor. The accuracy of representation depends on the resolution of the monitor screen which was 1920×1200 pixels in this research. Taking into account the geometry and shape of the grating as well as the area on the monitor screen designed for the grating image, this corresponds to ~72 pixels per single graduation pitch in the horizontal direction and ~600 pixels per graduation height. The values and are obtained automatically.
3. Modelling of the errors of the optical angular encoder
Geometrical errors inherited in the manufacturing process of the scale as well as ones acquired during the assembly are the main factors which are influencing the accuracy of the encoder. Therefore, a simulation model for the analysis of the influence of the encoder disc eccentricity and vibrations of disc center has been developed. The scheme of the geometric quantities which enables to determine the grating line position error is presented in Fig. 2.
Fig. 2Calculation scheme for actual position of a grating line and resulting line position error
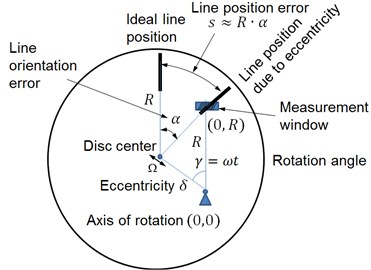
The reference line is (0, 0)-(0, ), thus the rotation axis (0, 0) and measurement window (0, ) relative position and orientation are regarded as fixed in space and time. In case of Moiré grating interaction it is assumed that the grating lines in the window are inclined at angle , however, the bottom line of the window is always horizontal. Ideally geometry of the transducer the center of the disc should always coincide with the rotation axis (0, 0) and a certain grating line (depicted by a thicker dark line in Fig. 2) can be observed at the center of the measurement window at a certain time. However, any misalignment of gratings and geometrical inaccuracies will cause measurement errors that can be defined by:
• Inaccuracies of the scale and window determined by random deviations of the grating lines positions with respect to their nominal positions;
• Eccentricity of the scale and/or rotation axis that can be treated in the same way in terms of the eccentricity of and ideal circle made of grating lines with respect to the rotation axis. Due to eccentricity, the changes of the orientation of grating lines within the window may occur (angle ), as well as, another grating line can be seen in the center of the window when compared with the case of zero eccentricity. This means that during the rotation of the disc erroneous number of grating lines passing through the window may be counted and therefore the disc rotation angle evaluation may be incorrect;
• Elastic vibrations of the body of the transducer that may cause the relative displacements of the window and the disc center. In this model the components of vibrations are represented by an additional displacement of the disc center as where – vibration frequency, , – sine and cosine components of the vibration amplitudes in the directions of Cartesian axes.
Such geometrical inaccuracies may be generalized and regarded as time dependent position of the center of a circular grating:
where – constant eccentricity, – rotation angle of the grating, see Fig. 2.
It is obvious that the eccentricity errors will change in time due to the rotation of the disc and due to elastic vibrations. The Fourier spectrum caused by such errors is obtained by simulating the grating interaction during the full rotation cycle of the disc. The grating line orientation error that is obtained as:
where , .
The error of the position of the grating line within the window is calculated:
It is assumed that the window is very narrow compared with the grating circle radius and orientation of several adjacent grating lines is approximately the same.
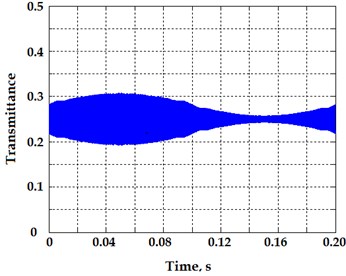
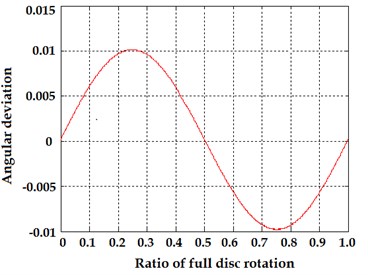
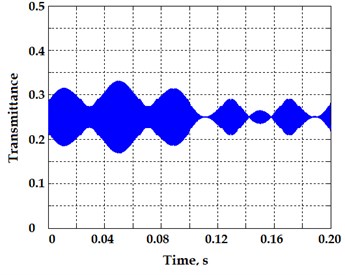
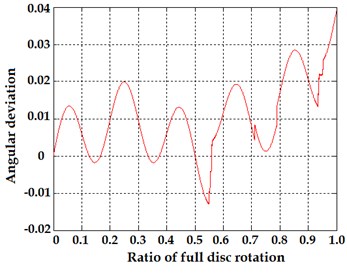
Fig. 3 and 4 present the light flux signals (left) and the calculated angular displacement error (right) correspondingly in cases of just simulated eccentricity of 0.01 and combined influence of eccentricity and vibrations with magnitude of 0.01 in and axis.
Fig. 3a) Transmittance function of Moiré gratings during full rotation of encoder disk and b) calculated angular error due to eccentricity of rotation axis of the disk
a)
b)
Fig. 4a) Transmittance function of Moiré gratings during full rotation of encoder disk and b) calculated angular error due to combined influence of eccentricity and vibrations
a)
b)
3.1. Numerical analysis of the encoder performance
General algorithm developed for the analysis of performance of optical encoders, shown in Fig. 5, can be employed and it enables to determine geometrical deviations of the encoder structure resulting from e.g. thermal deformations, vibrations, and assembly or graduation errors. The influence of these deviations on the optical signal of the interfering gratings is determined by employing the developed modelling software which simulates the interaction of two optical grating as described in previous section. The input data is geometry of both gratings as well as geometrical deviations governed by e.g. thermally induced deformations of the gratings and the output result is the transmittance function characterizing the changes of the light flux passed through the interfering gratings. Different outputs can be used for in-depth analysis of sensitivity of the encoder to possible design and assembly faults. Furthermore, information gained from simulated optical signals and Lissajous figures can be used for theoretical error estimation as it is described in [11].
Fig. 5Algorithm of numerical modelling for analysis of interference signal of the encoder’s gratings
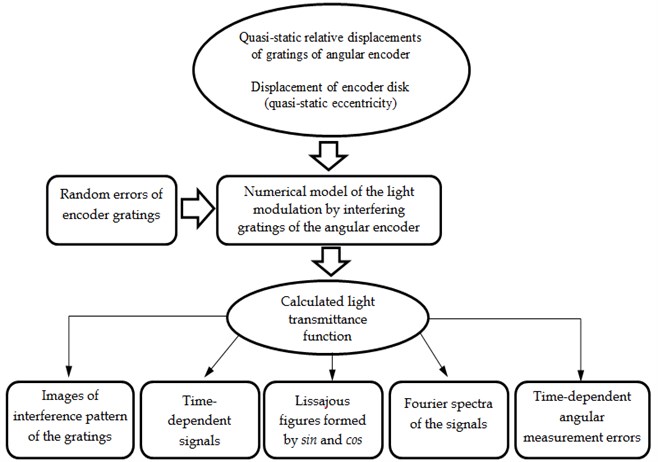
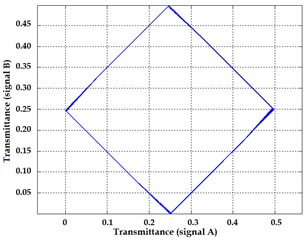
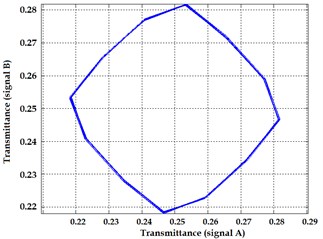
Fig. 6Lissajous figures obtained from numerical models for ideal gratings: obturative interaction a) and Moiré gratings b) and gratings with position deviations distributed by normal distribution (average value = 0, dispersion = dL/10) for obturative c) and Moiré interaction respectively d)
a)
b)
c)
d)
For the simulation of the grating interactions a computer program in MATLAB has been developed, the action of which is based on the image analysis of the grating interaction displayed on the monitor screen.
The Lissajous curves characterizing the grating interaction are obtained by representing two light flux signals obtained in two different measurement windows in and coordinate axes correspondingly. As a rule, the measurement windows are angularly displaced from each other at a certain angle and register two signals with phase (i.e. sine and cosine signals), where is the time during which the grating moves through one pitch, – integer number. In our research the sine and cosine signals are obtained by simulating interaction of graduations twice. During the second simulation the constant displacement of the moving graduation equal to 1/4 of the graduation period is added at each time moment.
Fig. 6 presents the Lissajous figures obtained by simulation in case of ideal gratings and gratings with random errors of grating lines. Here the cases of obturative (Fig. 6(a), (c)) and Moiré grating (Fig. 6(b), (d)) interaction have been analyzed. Distortions of Lissajous figures are increasing along with increasing angle between the lines of both gratings.
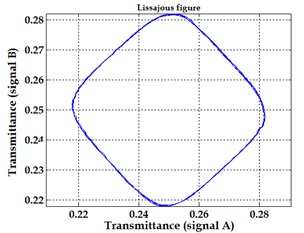
The simulated light flux signals of the Moiré grating combination at 85° Fig. 7(a) and corresponding Lissajous images Fig. 7(b) in case the vibration frequency of the disc centre exceeds 2 and 5 times the grating frequency are depicted in Fig. 7. In this simulation 120 measurement readings during the grating period are employed.
Fig. 7Optical signals obtained for Moiré interaction and corresponding Lissajous figures when encoder is excited by harmonic vibrations with frequencies exceeding the frequency of the grating signal 2 times a), b) and 5 times c), d)
a)
b)
c)
d)
3.2. Experimental setup
For the experimental analysis of the measurement signals generated by an optical angular encoder an experimental test system was employed. The main objective is to determine design or assembly faults, an appropriate configuration that resembles that of actual performance and to compare the obtained experimental results with the results of numerical simulation. Traditional test methods can be widely improved making use of signal analysis tools; although the Lissajous figure is a convenient graphical method, it is not well suited to make numerical analysis of the data. The aim is therefore to obtain an improved method that eases the evaluation of the encoder global performance and the particular signal deterioration.
Test setup consists of the appropriate drive system which is capable to drive up the encoder up to speeds 13 000 rpm and the encoder system attached to the drive as shown in Fig. 8.
The encoder signals connected to the signal recorder. A trigger signal line is established between the drive control and the signal recorder. The process starts when the drive begins to move. At this moment (through the trigger signal), the encoder signals A and B (voltages) start to be sampled with the specified frequency and recorded for later analysis. Later the test setup will be supplemented with vibration excitation and temperature measurement systems for the analysis dynamic and thermal behavior of the encoders.
Fig. 8Test setup for an angular optical encoder: 1 – angular encoder, 2 – mounting bracket, 3 – encoder coupling, 4 – drive system

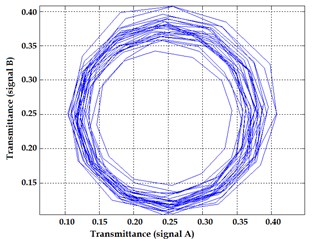
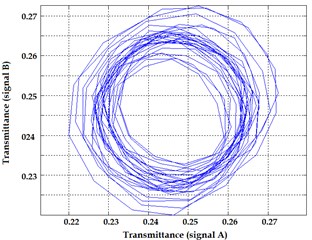
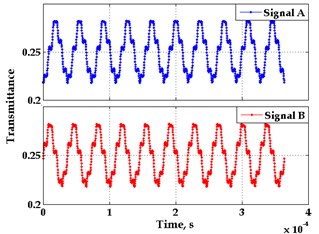
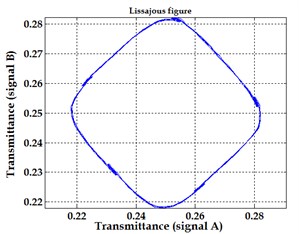
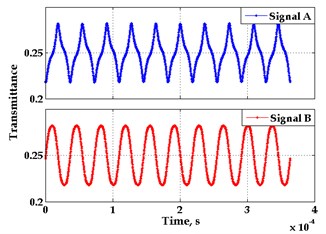
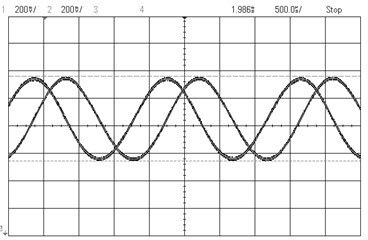
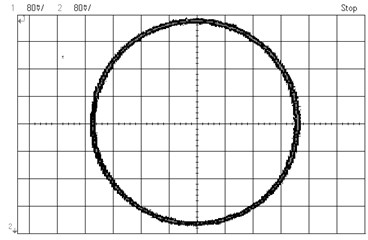
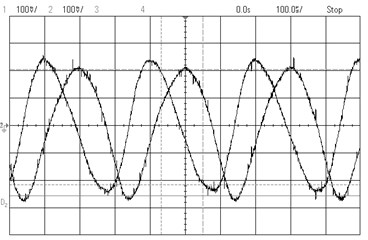
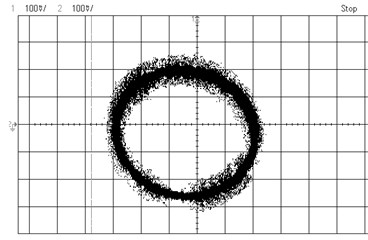
Fig. 9Experimental images of output signals of angular optical encoder and corresponding Lissajous figures for system without distortions a), b) and system with distortions c), d)
a)
c)
d)
The quadrature output signals obtained under correct performance of the encoder and when the system is affected by several distortions and their corresponding Lissajous images are presented in Fig. 9.
Most often different effects (graduation errors, eccentricity caused by assembly errors or vibrations, etc.) appear simultaneously in the output signals resulting in a distorted Lissajous image and total error in angular position estimation. Furthermore, geometrical deviations of main structural elements (housing, bearings, measurement and scanning gratings etc.) due to mechanical effects influence substantial variations of a measurement chain of the encoder and produce errors in the fringe patterns that are observed. Thus the relationships against the main metrological errors (zero-shift, amplitude ratio, phase difference, deviation from sine signal) can obtained from experimental images, analysis of sensitivities to individual error sources is more complex due to coupled effects and requires additional techniques particularly at the design stage of encoder systems.
4. Conclusions
The resolution of an optical incremental encoder is mainly determined by the quality of the interfering periodic structures. The analysis of interaction of such structures using classical geometric and spectral (Fourier) approach is limited due to aperiodic or random grating structures which are inevitable due to instrumental errors of the encoders therefore for the investigation of non-repetitive or random structures the developed numerical (binary) models are much more practical and effective tool as they enable not only direct and ostensive evaluation of the superposition images of the structures but also implication of different error sources in the numerical model.
It has been demonstrated the proposed algorithm enable thorough estimation of measurement errors caused by relative displacements and mechanical deformations of the structural components of a precision encoder due to geometrical errors, vibration or thermal inhomogeneity of the encoder structure.
Comparison of the results of numerical model of grating interaction with the known analytical (theoretical) results proved a good agreement between these results. The applied systematic methodology enabled us to optimize the performance of the optical encoder, to examine the influence of various factors affecting the encoder accuracy and to adjust the design of major components of the optical system.
References
-
Admiror I., Herch R. D. Analysis of the superposition of periodic layers and their Moiré effects through the algebraic structure of their Fourier spectrum. Journal of Mathematical Imaging and Vision, Vol. 8, 1998, p. 99-130.
-
Patorsky K., Kujawinska M. Handbook of the Moiré Fringe Technique. Elsevier, Amsterdam, 1993.
-
Zhou S., Fu Y., Tang X., Hu S., Chen W., Yang Y. Fourier-based analysis of moiré fringe patterns of superposed gratings in alignment of nanolithography. Optics Express Vol. 16, Issue 11, 2008, p. 7869-7880.
-
Amidror I. Glass patterns in the superposition of random line gratings. Journal of Optics A: Pure and Applied Optics, Vol. 5, 2003, p. 205-215.
-
Amidror I., Hersch R. D. Mathematical Moire models and their limitations. Journal of Modern Optics, Vol. 57, Issue 1, 2010, p. 23-36.
-
Amidror I. Moire patterns between aperiodic layers: quantitative analysis and synthesis. Journal of the Optical Society of America, Vol. 20, Issue 10, 2003, p. 1900-1919.
-
Amidror I., Hersch R. D. The role of Fourier theory and of modulation in the prediction of visible Moiré effects. Journal of Modern Optics, Vol. 56, Issue 9, 2009, p. 1103-1118.
-
Presnuchin L. N. Fotoelektričeskie Preobrazovateli Informacii. Moscow, 1974, (in Russian).
-
Barauskas R. Dynamic analysis of structures with unilateral constraints: numerical integration and reduction of structural equations. International Journal for Numerical Methods in Engineering, Vol. 37, 1994, p. 323-342.
-
Barauskas R. Techniques in the Dynamic Analysis of Structures with Unilateral Constraints. Structural Dynamic Systems Computational Techniques and Optimization: Nonlinear Techniques. Gordon and Breach Science Publishers, Netherlands, 1999, p. 131-194.
-
Sanches-Brea L. M., Morlanes T. Metrological errors in optical encoders. Measurement Science and Technology, Vol. 19, 2008, p. 115104.
Cited by
About this article
A. Barakauskas conceived the study and designed the experiments. R. Barauskas designed the numerical analysis algorithm and developed system models. A. Kasparaitis developed the experimental testing setup and conducted experiments. S. Kausinis developed methodology to numerical modelling of grating superposition errors. A. Jakstas carried out the experiments, data analysis and generalized the results.
