Abstract
Multi-fault diagnosis of rolling element bearing is significant to avoid serious accidents and huge economic losses effectively. However, due to the vibration signal with the character of nonstationarity and nonlinearity, the detection, extraction and classification of the fault feature turn into a challenging task. This paper presents a novel method based on redundant second generation wavelet packet transform (RSGWPT), ensemble empirical mode decomposition (EEMD) and optimized least squares support vector machine (LSSVM) for fault diagnosis of rolling element bearings. Firstly, this method implements an analysis combining RSGWPT-EEMD to extract the crucial characteristics from the measured signal to identify the running state of rolling element bearings, the vibration signal is adaptively decomposed into a number of modified intrinsic mode functions (modified IMFs) by two step screening processes based on the energy ratio; secondly, the matrix is formed by different level modified IMFs and singular value decomposition (SVD) is used to decompose the matrix to obtain singular value as eigenvector; finally, singular values are input to LSSVM optimized by particle swarm optimization (PSO) in the feature space to specify the fault type. The effectiveness of the proposed multi-fault diagnosis technique is demonstrated by applying it to both simulated signals and practical bearing vibration signals under different conditions. The results show that the proposed method is effective for the condition monitoring and fault diagnosis of rolling element bearings.
1. Introduction
Rolling element bearing is one of the most common components in modern rotating machinery. The failure of rolling element bearings can result in the deterioration of machine operating conditions [1]. Therefore, the reliable bearing fault detection techniques are very significant to prevent the degradation of performance and malfunctions. Bearing fault detection can be carried out using different techniques such as vibration signals, lubricant information, and acoustic and temperature data [2]. Among them, vibration signals carry rich condition-related information that a series of impact impulses will occur when a rolling element bearing has a localized fault [3, 4]. Therefore, vibration-based analysis is widely applied in the fault diagnosis of rolling element bearings [5-7]. Many vibration analysis methods have been presented for the fault diagnosis of rolling element bearing in the time domain, the frequency domain and the time-frequency domain, respectively [8]. However, the vibration signal of rolling element bearings is nonlinear and nonstationary signal. It is very difficult to identify the fault of the rolling element bearing only in the time domain or the frequency domain.
Wavelet transform (WT) method possesses perfect local property in both time domain and frequency domain, which is used widely in the field of machinery fault detection and identification [9]. But the high frequency band of signal, which always exist the modulation information of the fault bearing, cannot be accurately split by the WT. Second generation wavelet packet transform (SGWPT) is a new wavelet construction method. The time-frequency resolution of SGWPT varies with the decomposition levels, and hence the detail coefficients at each level are further decomposed to obtain their approximation and detail components [10, 11, 28]. However, SGWPT do not have time invariant property in the decomposition of a signal. This may result in the loss of useful fault information for feature extraction [12]. The redundant lifting scheme based SGWPT can not only provide more detailed local feature description of the signal, but also inhibit the frequency aliasing components of the analysis result [13]. Therefore, the features extracted from the transform coefficients of RSGWPT have a greater ability to detect the fault signal. Empirical mode decomposition (EMD) offers a different approach to the nonstationary and nonlinear signal processing in the time-frequency domain. It is based on the local characteristic time scales of a signal and could self-adaptively decompose the complicated signal into a set of intrinsic mode functions (IMFs) [14]. Therefore, the EMD method has received more attention for its application in fault diagnosis of rolling element bearings [15]. However, when the EMD method is applied to the nonlinear and nonstationary signals, the original signal cannot be accurately decomposed because of mode mixing, the end effects and the unexplainable negative frequency. Wu and Huang developed ensemble empirical mode decomposition (EEMD) to improve EMD. By adding noise to the original signal and calculating the means of the IMFs repeatedly, EEMD is more accurate and effective for signal decomposition [16].
After feature extraction, an intelligent classifier is needed. Artificial neural networks (ANN) have been successfully applied to the fault diagnosis [17]. However, the ANN methods have some drawbacks, such as a locally optimal solution, low convergence rate, obvious over-fitting and especially poor generalization when the number of samples for fault diagnosis is limited [18]. Support vector machines (SVM) based on statistical learning theory have better generalization than ANN, and guarantee the local and global optimal solution are exactly the same [19]. Meantime, SVM can solve the learning problem with a smaller number of samples. However, in practical applications, the classification result of the practically implemented SVM has been often far from the theoretically expected level, because their implementations are based on the approximated algorithms due to the high complexity of time and space [20]. To improve the limited classification performance of SVM, LSSVM method provides the equality constraints and regards the sum of squared error loss function as experience loss of training set [21]. It transforms solving quadratic programming problem into solving linear equations problem. Compared with SVM, LSSVM has a faster solution speed and higher solution accuracy.
To more accurately extract fault features and fault identification, we proposed a novel method for fault diagnosis of rolling element bearings in this paper. The vibration signal is adaptively decomposed into a number of IMFs by RSGWPT-EEMD, two step screening processes based on the energy ratio are introduced to carry out the screening of IMFs. The matrix is formed by different level IMFs, and SVD is used to decompose the matrix to obtain the singular value as eigenvector. Singular values are input to LSSVM to specify the fault type. In order to obtain a high level classification model of rolling element bearings, the PSO algorithm is applied to carry out the parameter optimization in the feature space.
The rest of the paper is organized as follows. In Section 2, the fault feature extraction based on RSGWPT and EEMD will be introduced, while singular value extraction based on SVD will be described in Section 3. In Section 4, we use optimized LSSVM to accomplish the fault classification based on the selected features. Section 5 will present the experimental results and analysis, the proposed method is applied to diagnose different states of rolling element bearings, and the results have verified the validity of the proposed method. Finally, the conclusion is drawn in Section 6.
2. Fault feature extraction based on proposed RSGWPT-EEMD
2.1. Redundant second generation wavelet packet transform
The RSGWPT is constructed by applying the redundant lifting scheme on the SGWPT. In the redundant lifting scheme, and represent the prediction and update operators of the redundant lifting scheme at level , the coefficients of and are obtained by padding and of initial operator and withzeroes [11]:
According to the redundant lifting scheme and SGWPT, the RSGWPT is constructed. The decomposition procedure of RSGWPT at the level are achieved by using and , which are described as below:
The reconstruction procedure of RSGWPT can be obtained from its decomposition procedure, which consists of inverse update step, inverse prediction step and merging step:
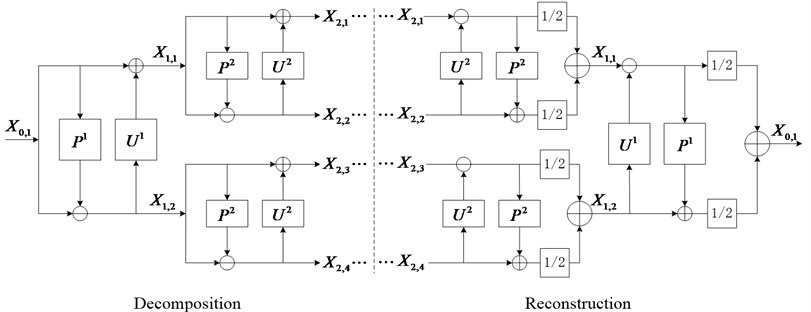
The forward and inverse transforms of RSGWPT are shown in Fig. 1. Owing to without the split operation in the decomposition stage of RSGWPT, the approximation and detail coefficients at all levels have the same length as that of the input signal. Consequently, the decomposition results of RSGWPT possess time invariant property and keep the information of the raw signal perfectly.
2.2. Ensemble empirical mode decomposition
The empirical mode decomposition (EMD) is a non-linear multi-resolution self-adaptive decomposition method. One major drawback of EMD is the mode mixing. Therefore, Wu and Huang [16] proposed EEMD to alleviate the mode mixing occurring in EMD. EEMD decomposes the signals by the noise-assisted analysis technology and has been demonstrated to have better scale separation ability than EMD. The decomposition procedure is described as follows.
(a) Suppose an original signal , add a white noise series with the given amplitude to the original signal:
where indicates the th added white noise series, and represents the noise-added signal of the th trial.
(b) Decompose the white noise-added signal into IMFs by EMD, and can be obtained:
where and in dicate the th IMF and residue of the th trial, respectively.
(c) Repeat steps (a) and (b) until , in which the amplitude of added white noise is fixed.
(d) Calculate the ensemble means of corresponding IMFs obtained in the above decomposition trials by:
where 1, 2,…, , 1, 2,…, ; is regarded as the final th IMF and is regarded as the final residual signal.
Therefore, the signal can be represented as:
Fig. 1The decomposition and reconstruction stages of RSGWPT
2.3. RSGWPT-EEMD method for fault feature extraction
EEMD is suitable to process nonlinear and non-stationary signal, and can decompose a complex signal into a set of natural IMFs according to the signal local feature. However, it is difficult to extract weak frequency components. When there is a fault in the rolling element bearings, the useful characteristic frequency components generally contain very little energy and are submerged by background noise. The background noise has a wide frequency band and higher-level macrostructural vibrations, and it is difficult to extract the useful characteristic components [22, 23]. To solve this problem, RSGWPT is used as a preprocessor to separate the frequency components into a list of narrow bands and provide better time-frequency localization of the input signal. Hence, the characteristic frequency components can be extracted easily at different narrow bands using EEMD. In this section, the combination of EEMD with RSGWPT as a preprocessor and two-stage screening processes based on energy criteria is called RSGWPT-EEMD. The procedures of the proposed method are given as follows.
The discrete signal , can be written as:
where is the length of the signal. By computing -level RSGWPT, the signal is decomposed into sets of sub-band coefficients with the length of . The sequence of these sets at the th level is and each set of these coefficients can be viewed as a node in a binary wavelet packet tree. The decomposition coefficients can be given:
Each node of the RSGWPT tree is indexed with a pair of integers ( where is the corresponding level of decomposition and is the order of the node position in the specific level. From the decomposition coefficients , a reconstructed signal of length can be obtained by implementing the redundant second generation wavelet packet reconstruction. In reconstruction procedure, the coefficients to be reconstructed are reserved, and the other coefficients in level are set to be zero, and .
The redundant IMFs have not only lower frequency than the lowest frequency of the signal but also less amplitude. This can be explained that the redundant IMFs are generated due to leaking in the decomposing process of EEMD. Therefore, if the energy of is almost equal to that of , is viewed as the redundant reconstructed signal. The energy ratio of to will be constructed to eliminate the redundant IMFs [24].
It is defined as:
If is less than (in general, ), are viewed as the real IMF. The energy ratio criterion is logical to eliminate the redundant IMFs. It is based on the fact that the redundant IMFs has a lower frequency and less amplitude than the lowest frequency of the signal .
Next, the significance of feature packets can be assessed quantitatively by introducing the 1st level screening processes which use the energy ratio between and signal as given in:
where is the difference between the input signal and . On the other hand, represent time series wavelet packet coefficients with th packet on th resolution.
When the 1st screening process is finished, the process of EEMD will be applied to decompose the selected feature packet data sets. Next, the resultant IMFs from each selected feature packet is stored as preselected IMFs data sets. Subsequently, the energy ratio as given in Eq. (13), is used in the 2nd level screening processes. The purpose of 2nd screening processes is to identify and select the most vital IMFs from the list of IMFs data sets:
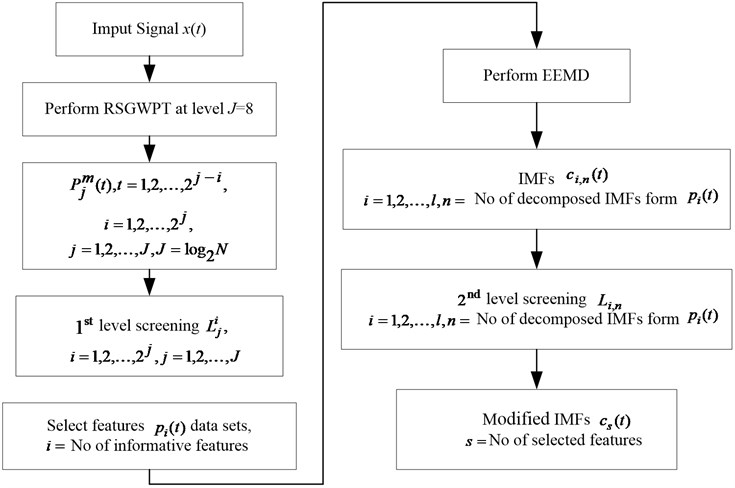
In order to extract vital signal features, computing energy ratio is an important step as part of this algorithm. For those with energy ratio lower than 0.99 thresholds, their corresponding is viewed as a real IMF and subsequently stored in the finalized data sets . Those IMFs, which are stored in the data sets , are defined as “modified IMFs”. Otherwise, it is recognized as a redundant IMF and therefore will be eliminated. The operation procedure of RSGWPT-EEMD is summarized in Fig. 2.
Fig. 2Flow chart of the proposed RSGWPT-EEMD based two step screening
2.4. Simulation analysis using proposed RSGWPT-EEMD
To quantitatively evaluate the effectiveness of the proposed RSGWPT-EEMD method, a signal is simulated as shown in Fig. 3. The signal sampled at 2048 Hz comprises of two carrier frequency components (100 and 300 Hz) over the entire time domain, and are modulated by 20 and 50 Hz. The purpose of this simulation is to simulate the phenomenon that fault vibration signal is multi-component modulation signal. In practice, noise existing in the original signal often behaves like white noise, it covers the entire frequency domain. A white noise with signal to noise ratio of 1dB is added into the input signal. The simulated signal is expressed as follows:
Fig. 3Time domain plot of the simulated signal
The simulated signal is analyzed with the conventional EMD, EEMD and the proposed RSGWPT-EEMD respectively to demonstrate the effectiveness of the energy ratio selection criterion and the proposed method, and Fig. 4, 5 and 6 illustrate the decomposition results of IMFs and corresponding frequency spectrum. The calculation results of the energy ratio are listed in Table 1 and 2.
Fig. 4The decomposition results and corresponding frequency spectrum of IMFs with EMD
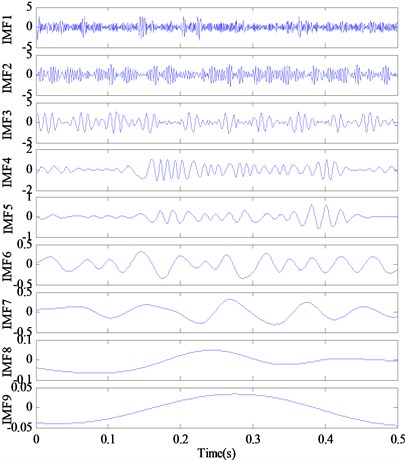
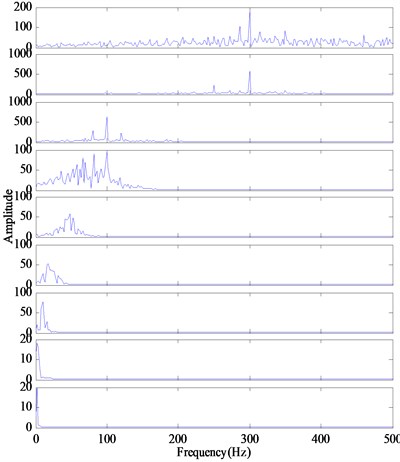
The decomposition results of the conventional EMD and their Fourier-based spectrums are shown in Fig. 4. It can be seen from Fig. 4 that the obtained IMFs distort the useful harmonic components. The IMF1 and IMF2 in Fig. 5 contain the carrier frequency 300 Hz, but not its sideband frequencies 250 and 350 Hz. And there is the heavy noise. These reveal that multiple frequency components contained in the signal cannot be decomposed sufficiently by EMD.
The EEMD decomposition result of the signal and their Fourier-based spectrum are shown in Fig. 5, where the added white noise amplitude is 0.25 times the standard deviation of the signal, and the number of ensemble is 200. As illustrated in Fig. 5, the first IMF consists of three main frequency components, which are the carrier frequency 300 Hz and its two sideband frequencies 250 and 350 Hz. The second IMF mainly consists of the carrier frequency 300 Hz and the third IMF mainly consists of the carrier frequency 100 Hz and its two sideband frequencies 80 and 120 Hz. However, the rest of the IMFs contain a lot of redundant low-frequency components. Therefore, the first three IMFs are more informative than other IMFs. In other words, only the first three IMFs are real components of the signal and the others are the pseudo components that have low frequency and mislead our analysis.
Fig. 5The decomposition results and corresponding frequency spectrum of IMFs with EEMD
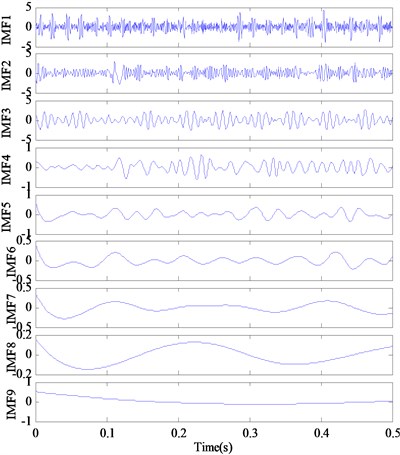
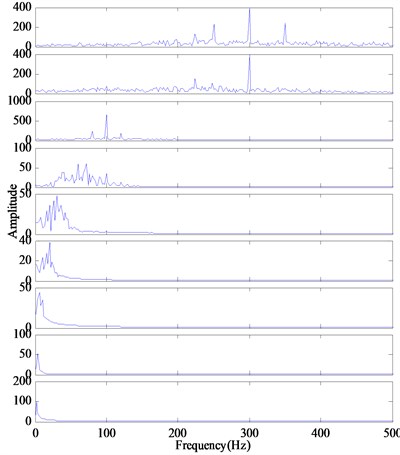
Fig. 6The decomposition results with proposed RSGWPT-EEMD
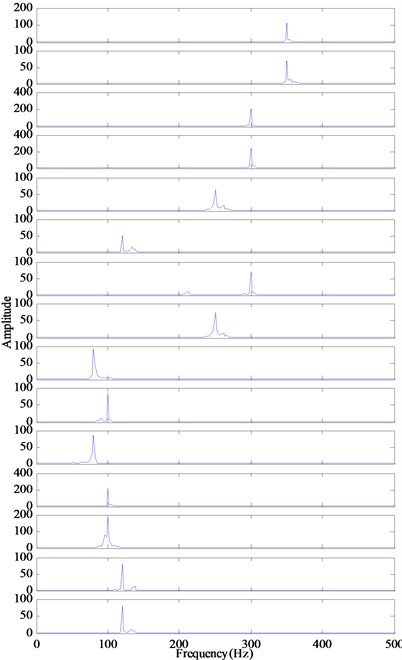
Considering the calculated energy ratio with EEMD listed in Tables 1 and 2, it can be seen that the energy ratio values of the first three IMFs are lower than 0.99. According to the energy ratio selection criterion, the first three IMFs are viewed as the meaningful IMFs and the other are the redundant IMFs, which coincide with the analyzed results of the decomposition results shown in Fig. 5. It can be found that the IMFs with the low energy ratio are more informative than other IMFs.
Table 1The energy ratios of between filtered signal and each IMF
Method | Energy Ratio | |||||||
IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | |
EMD | 0.6473 | 0.7327 | 0.6517 | 1.0032 | 1.0057 | 1.0054 | 1.0004 | 1.0017 |
EEMD | 0.5074 | 0.7252 | 0.6341 | 0.9913 | 0.9963 | 0.9974 | 0.9975 | 1.0008 |
Proposed method | 0.0296 | 2.7829e-6 | 0.0120 | 0.9860 | 0.0134 | 0.9848 | 0.0126 | 0.9855 |
Table 2The energy ratios of between filtered signal and each IMF (continue table 1)
Method | Energy Ratio | ||||||
IMF9 | IMF10 | IMF11 | IMF12 | IMF13 | IMF14 | IMF15 | |
EMD | 1.0009 | – | – | – | – | – | – |
EEMD | 1.0072 | – | – | – | – | – | – |
Proposed method | 0.0124 | 0.9857 | 7.2098e-4 | 0.0529 | 8.6238e-6 | 0.0182 | 0.0212 |
The IMFs obtained by conventional EMD and EEMD in Fig. 4 and 5 cannot fully represent the real frequency pattern of the signal. Then the proposed method is applied to analyze the simulated signal. The modified IMFs and their Fourier-based spectrum are illustrated in Fig. 6. It can be seen that the proposed method can detect the carrier frequencies (100 Hz, 300 Hz) and their sideband frequencies (80 Hz, 120 Hz, 250 Hz, 350 Hz). In addition, there are unnecessary components in the decomposition result of the proposed method. Different from the results of EMD and EEMD method, in which there exist many unnecessary IMFs and the IMFs are highly corrupted with noise, the RSGWPT-EEMD technique can effectively remove noise of the signal and extract meaningful IMFs. From Table 1 and Table 2, it can be seen that all the modified IMFs generated by the RSGWPT-EEMD have a low energy ratio. With energy ratio selection criterion, all the modified IMFs are meaningful IMFs, which are demonstrated by analyzing results of the decomposition results shown in Fig. 6. It can be seen that all those modified IMFs are more informative than the original IMFs generated by the EMD and EEMD.
Fig. 7The Hilbert marginal spectrum by using EMD
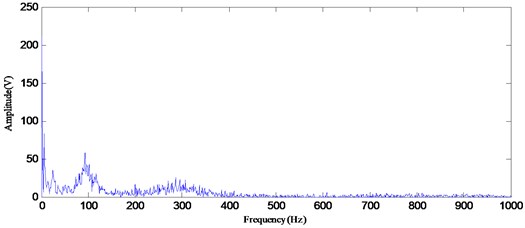
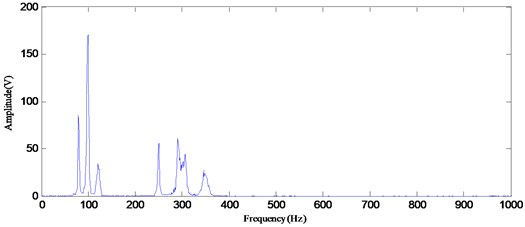
To compare the proposed approach with the conventional mechanical fault diagnosis methods, the marginal spectrum analysis method based on Hilbert transform was applied to detect the simulated signal of the rolling bearing. Fig. 7 and 8 illustrate the Hilbert marginal spectrum by using EMD and EEMD, respectively. It can be seen from Fig. 7 and 8 that they only present the one carrier frequency of 100 Hz, and there is heavy noise in the whole frequency band. This may result in the ambiguous identification result. The Hilbert marginal spectrum by using the proposed method as illustrated in Fig. 9 has generated some quite definite result in presenting all frequency components that are existed in signal. From the result of the marginal spectrum, the frequency of the modulating signal causes sideband signals to appear at frequencies above and below the carrier frequency . Therefore, for each frequency component in the modulating signal, an upper sideband appears above , and a lower sideband appears below . As shown in Fig. 9, 20 and 50 Hz modulation frequencies are readily identified as sidebands. These frequencies appeared around the carrier frequencies of 100 and 300 Hz, respectively. Moreover, most of noise related frequency components are removed. According to the comparison, the marginal spectrum based on RGSWPT-EEMD presents a much clearer message about the frequency components embedded in the simulated signal.
According to the comparison above, the RSGWPT-EEMD has shown its robustness in analyzing high noise contaminated signal, at where its capability to extract all instantaneous frequencies from the input signal has been proven
Fig. 8The Hilbert marginal spectrum by using EEMD
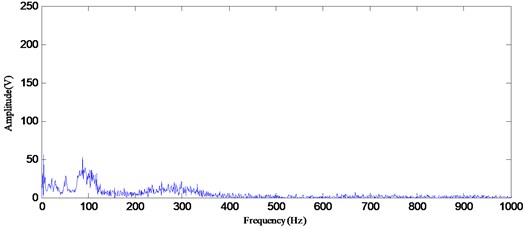
Fig. 9The Hilbert marginal spectrum by using RSGWPT-EEMD
3. Fault singular value extraction based on SVD
In the matrix theory, singular values generated by SVD present the inherent feature of the matrix and possess the characteristics of favorable stability, scale invariance and rotating invariance. Hence, the singular values of the matrix whose rows are modified IMFs are very feasible to be the feature vector for LSSVM training and testing.
The matrix consists of a set of modified IMFs is divided to two initial feature matrices and , they are described respectively by:
If is even, . Otherwise, . The substantive features of the disturbing signal are characterized by the matrix and .
Let be a real matrix with rows and columns. There exist orthogonal matrices and with the size of and such that [29]:
where is a diagonal matrix with nonnegative diagonal elements. These diagonal elements (1, 2,…, ) arranged in descending order are termed the singular values of the matrix .
Then the initial feature matrices and are processed by the SVD respectively, the obtained singular values and are expressed as follows:
where , . The vector is chosen as the feature vector.
4. Fault feature classification based on the improved LSSVM-PSO
For a given training set of data points , is the input data and is the output data. A nonlinear function is employed to map the original input space to a high dimensional feature space . Then the linear decision function is constructed in this high dimensional feature space [27]:
Thus for LSSVM estimation, the following optimization problem is formulated:
where is a regularization factor, and is the difference between the desired output and the actual output.
The Lagrange multiplier is introduced to solve the constrained optimization. The objective function can be obtained:
The conditions for optimality are given by:
The resulting LSSVM model can be evaluated at a new point as follows:
where and are the solutions to Eq. (20), and is the kernel function.
The particle swarm optimization is one of the newest evolutionary computational techniques which has been applied to solve the complex optimization problems perfectly. In this study, the particle swarm optimization is used to enhance the approximation accuracy of LSSVM.
5. Experimental analysis and discussion
In order to verify the feasibility and effectiveness of the proposed method, the actual experiment on fault identification of rolling bearings is conducted in this paper. The vibration data of rolling bearings are provided by Case Western Reserve University (CWRU) [25]. The vibration data with the defect size of 7 mills and 14 mils are chosen to be sample signals in this paper, and the motor load is 0 hp. Selected sampling signals respectively from the four bearings, where the first one is normal, the second one is with inner raceway fault, the third one is with outer raceway fault (at 6:00 directions) and the last one is with rolling element fault. For each sampling signal that represents one working condition, the first 120000 points (the sampling time is 10 s) are divided into 40 sub-signals. Each sub-signal contains 3000 points (the sampling time is 0.25 s). As a result, 40 samples are acquired for each working condition, and there are 7×40 samples in total. Each sampling signal is different from each other and there is no overlap between any two sampling signal.
Fig. 10Time domain plot of the signal with outer race defect
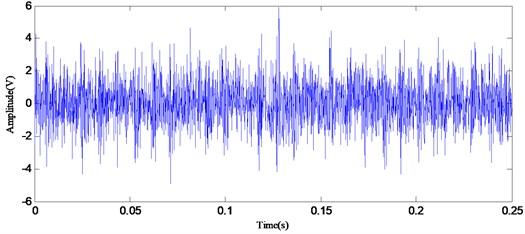
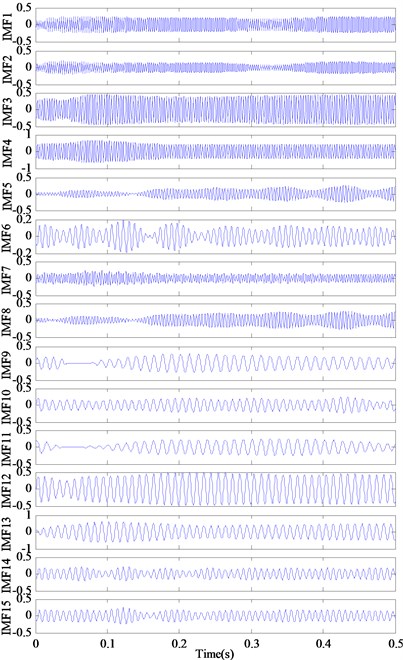
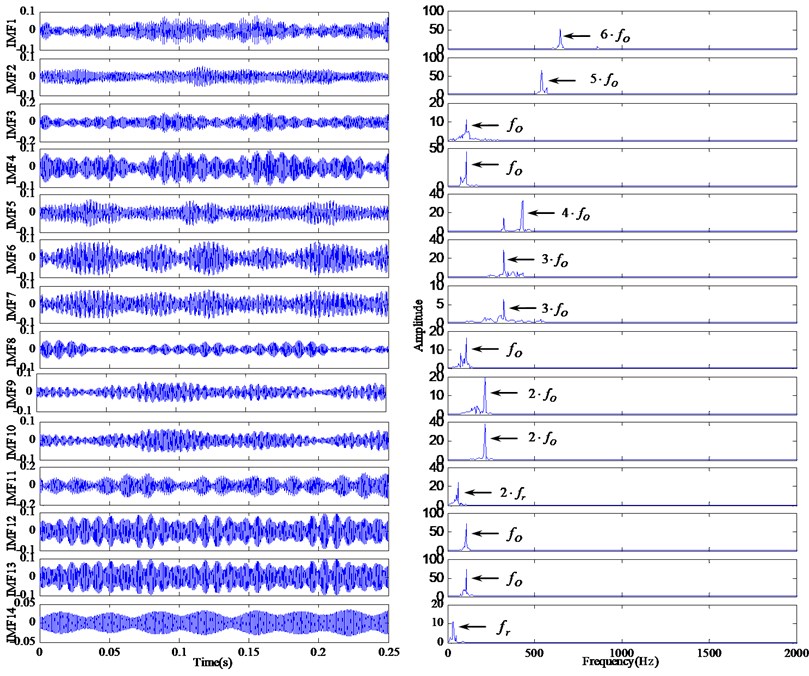
Fig. 10 illustrates representative waveforms of outer race defect with motor load 0 hp and diameters 0.007 in. Through the proposed RSGWPT-EEMD method, 14 modified IMFs can be acquired. Fig. 11 shows the decomposition results and corresponding envelope spectrum of modified IMFs. While operating a rolling element bearing with local fault, the impulse is created, the high-frequency shock vibration is then generated and the vibration amplitude is modulated by the impulse force [5]. In order to obtain the fault characteristic frequency, the vibration signal of rolling element bearing need to demodulate. It is generally difficult to directly extract the fault information from the vibration signal because of the complexity of its waveform. Conceptually, the EMD method is equivalent to a filtering process, and the IMFs obtained can be treated as the vibration signal component within the specific frequency band. The envelope analysis can thus be employed on the IMF to examine the fault characteristic frequencies.
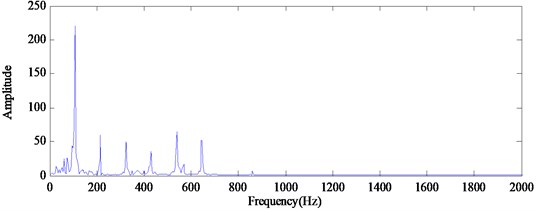
The theoretic characteristic frequency of the roller bearing with outer race fault is calculated as 107 Hz. It can be observed in Fig. 10 that the fault feature is so weak that it is drowned by the background signals relevant to the rotational speed of the rotor and other noise. From Fig. 11 it can be seen that there are obvious spectral lines at the characteristic frequency of outer race fault (107 Hz) and its harmonic frequencies. According to the analysis results, it can be determined there are defects on the outer race without any trouble.
Fig. 11The decomposition results and demodulated spectrum of modified IMFs for outer race defect using RSGWPT-EEMD
In order to demonstrate the improvement of the modified IMFs obtained by the proposed method, the vibration acceleration signal is also decomposed by the conventional EMD and EEMD. Fig. 12 presents the IMFs of the EMD method and the demodulation results of the IMFs. It can be seen that there are no obvious lines at the corresponding positions (1, 2, 3, 4, 5). With EEMD method, the 1th-10th IMF components are obtained. The obtained demodulated spectrums are shown in Fig. 13, which are compared with the demodulated results with conventional EMD shown in Fig. 12. It reveals that only the first IMF contains the fault characteristic frequency information (107 Hz, 214 Hz), the others are irrelevant or noise related. It can be concluded that the conventional EMD with the mode mixing phenomenon would causes the inaccurate diagnosis results, the EEMD method can overcome the limitations which occur in the conventional EMD, whereas there also are many redundant components. Compared to EMD and EEMD, the RSGWPT-EEMD can not only eliminate the redundant IMF components but also reduce the effect of noise. It is clear that the proposed method can extract the characteristic frequency component.
Fig. 14, 15 and 16 show the demodulated spectrum results of the related method. From Fig. 14 and 15, we can observe the characteristic frequency (107 Hz, 214 Hz), but there is heavy background noise. The useful information for detecting the failure is not very clear in the demodulated spectrum. From Fig. 16 we can clearly observe the characteristic frequency (107 Hz) and its harmonics (214 Hz, 321 Hz, 428 Hz, 535 Hz, 642 Hz). Compared the demodulated spectrum using RSGWPT-EEMD versus the demodulated spectrum shown in Fig. 14 and 15, it is seen that RSGWPT-EEMD can effectively remove the noise signal and highlight characteristic frequency components. In all the analyzed results, although the EMD and EEMD can also detect the characteristic frequency of outer race fault, the proposed method outperforms other related techniques with more obvious characteristic frequency.
Fig. 12The decomposition results and demodulated spectrum of IMFs for outer ring defect using EMD
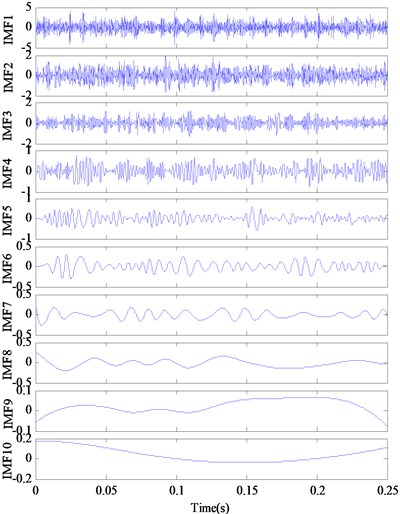
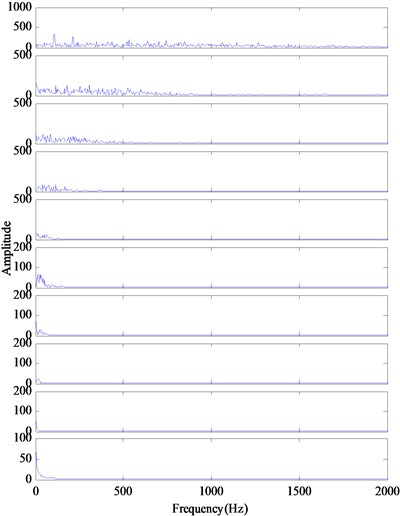
Fig. 13The decomposition results and demodulated spectrum of IMFs for outer race defect using EEMD
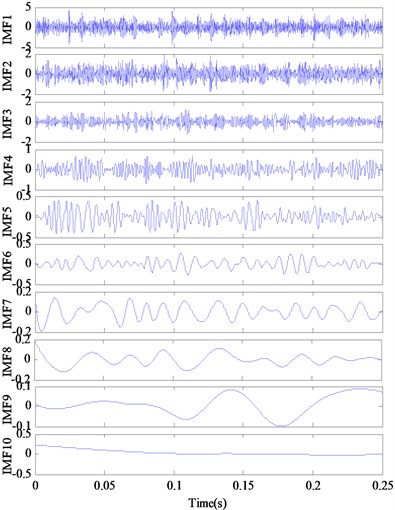
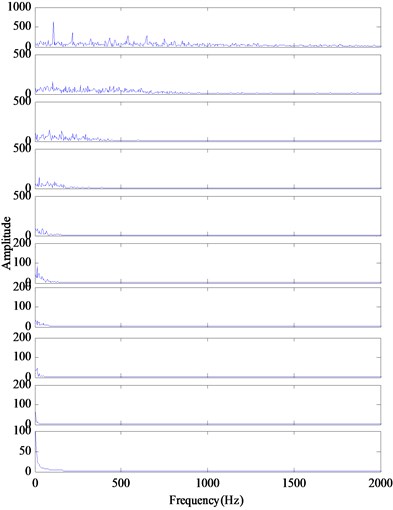
Fig. 14The demodulated spectrum of outer race defect using EMD
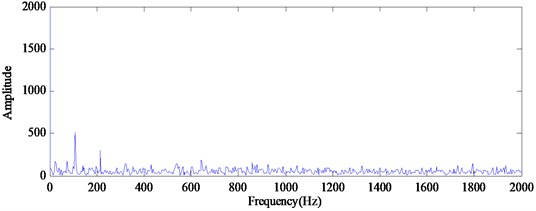
Fig. 15The demodulated spectrum of outer race defect using EEMD
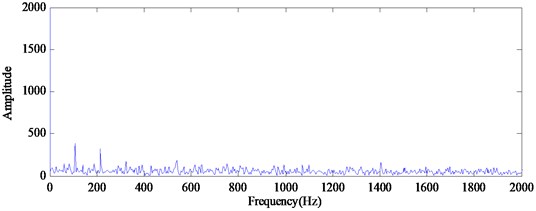
Fig. 16The demodulated spectrum of outer race defect using RSGWPT-EEMD
In order to provide an intuitive distinguishing result, LSSVM is used to diagnose the bearing condition after RSGWPT-EEMD. Through analyzing the modified IMFs obtained by the proposed RSGWPT-EEMD, it is found that these modified IMFs represent useful fault characteristic frequency components. Hence, the modified IMFs of each sample are chosen to form the initial feature matrix. Then, SVD technique is applied to the feature matrix to generate the feature vector which consists of singular values. Consequently, for each working condition, a matrix of the feature vector is generated.
The feature vectors are divided into training samples and testing samples. 10 sets of the feature vectors, from the four bearing states respectively, are used for training purpose and the rest 30 sets of each state are used for testing. The detailed descriptions of the three data sets are shown in Table 3. The training sets are input to multi-fault classifier LSSVM optimized by improved PSO, and the optimal regularization parameter and kernel parameter are obtained after flexibly adjusted. Then, the testing sets are input to the trained network, and the different conditions of rolling bearings are identified.
For avoiding the tweak problem, each experiment is repeated 30 times, and the average classification accuracy of three data sets is listed in Table 4. To show the superiority of the feature extraction by SVD based on RSGWPT-EEMD, SVD based on WPT, RSGWPT, EMD and EEMD are used for vibration signal’s feature extraction respectively. In order to demonstrate the efficiency of the LSSVM-PSO, a comparison between the LSSVM-PSO and SVM with the same feature extraction is done.
Table 3The detailed descriptions of the three data sets
Data set | The number of training samples | The number of test samples | Defect size (inches) | Operating condition | Label of classification |
A | 10 | 30 | 0 | Normal | 1 |
10 | 30 | 0.007 | Outer ring | 2 | |
10 | 30 | 0.007 | Inner ring | 3 | |
10 | 30 | 0.007 | Rolling element | 4 | |
B | 10 | 30 | 0 | Normal | 1 |
10 | 30 | 0.021 | Outer ring | 2 | |
10 | 30 | 0.021 | Inner ring | 3 | |
10 | 30 | 0.021 | Rolling element | 4 | |
C | 10 | 30 | 0 | Normal | 1 |
10 | 30 | 0.007 | Outer ring | 2 | |
10 | 30 | 0.007 | Inner ring | 3 | |
10 | 30 | 0.007 | Rolling element | 4 | |
10 | 30 | 0.021 | Outer ring | 5 | |
10 | 30 | 0.021 | Inner ring | 6 | |
10 | 30 | 0.021 | Rolling element | 7 |
Table 4The fault identification of based on relevant method
Algorithms | Classification accuracy of data set A (%) | Classification accuracy of data set B (%) | Classification accuracy of data set C (%) | Difference between data set (%) |
EMD+LSSVM-PSO | 95.60 | 95.58 | 88.19 | 7.41 |
FEEMD+LSSVM-PSO | 95.92 | 95.97 | 89.06 | 6.86 |
WPT+LSSVM-PSO | 96.67 | 96.75 | 89.86 | 6.89 |
RSGWPT+LSSVM-PSO | 97.64 | 97.50 | 90.97 | 6.67 |
RSGWPT-EEMD+SVM | 98.28 | 98.36 | 98.25 | 0.11 |
RSGWPT-EEMD+ LSSVM-PSO | 99.16 | 99.19 | 99.13 | 0.06 |
For all the data sets, it can be noticed that the test accuracy of RSGWPT-LSSVM-PSO (77.64 %, 97.5 %, 90.97 %) is higher than that of the WPT (96.67 %, 96.75 %, 89.86 %) and the test accuracy of EEMD-LSSVM-PSO (95.92 %, 95.97 %, 89.06 %) is higher than that of the EMD (95.6 %, 95.58 %, 88.19 %). It can be explained by the fact that RGSWPT provides an entirely spatial domain interpretation of the transform, as opposed to the traditional WPT. Similarly, EEMD overcomes the mode mixing problem of EMD and increases the decomposition precision of vibration signals. Thus, the features extracted by SVD based on EEMD are more representative than features extracted by SVD based on EMD which has been reported in the literature [26]. Moreover, the proposed method based on RSGWPT-EEMD, SVD and LSSVM-PSO provides better classification accuracy (99.16 %, 99.19 %, 99.13 %) compared with all the other four methods. The RSGWPT-EEMD combines advantage of RSGWPT and EEMD, and at the same time it eliminates most of redundant features. Hence, the feature extraction ability of the proposed method is significantly stronger than the previous four methods. Meanwhile, it is clear that the LSSVM-PSO classifier has higher accuracy than SVM in classification with the same feature extraction. Therefore, the performance of LSSVM-PSO classifier with RSGWPT-EEMD feature extraction is superior.
In the case of data sets C, the classification accuracies (range from 88.91 % to 99.13 %) of all the method are lower than that of data set A or B, which can be explained by the large number of classes (seven classes) than data sets A or B (four classes). With the class number increasing the advantage of RSGWPT-EEMD+LSSVM-PSO is more prominent. When the detection class number is 7, it is clear from Table 4 that the performance of RSGWPT-EEMD+LSSVM-PSO is significant better than that of other methods. In data set A or B, 4 working conditions were considered, the test accuracies of the proposed method are also higher than the other methods but it is not as significant as in data set C.
The difference of classification accuracy between different data set with the same method is also illustrated in Table 4. It can be seen that with the class number increases, the deviations of classification accuracy of RSGWPT-EEMD+LSSVM-PSO is smallest (0.06 %). It is obvious that the proposed method presents much stronger stability as compared to other approaches. These combined results indicate that the proposed method has the highest identification accuracy, and is a powerful fault diagnosis algorithm for rolling element bearings.
Furthermore, three groups of experiments are carried out for further studying of the application of the proposed method in the fault identification. With the data set which remains containing 160 data samples, the data set is split differently 20, 40, 60 and 80 samples for training and the calculation procedure is the same as above. Table 5 shows the influences of the number of training samples on the identification accuracy. It can be seen from Table 5 that the larger number of training samples yield higher identification accuracy, and the highest classification accuracy (100 %) is arrived when the size of training sets is 60. It also can be found that the proposed method can still classify the four conditions of rolling bearing after the training samples are decreased, which confirms that this method can be applied successfully to the fault identification even in cases where only limited training samples are available.
Table 5The results of faults identification using different training sets and testing sets
Methods | Training sample | Test sample | Overall classification accuracy [%] |
RSGWPT-EEMD+SVD +LSSVM-PSO | 20 | 140 | 97.14 |
40 | 120 | 98.33 | |
60 | 100 | 100 | |
80 | 80 | 100 |
6. Conclusions
This paper proposed a novel method based on RSGWPT-EEMD, SVD and LSSVM-PSO for multi-fault diagnosis of rolling element bearings. Two series of screening processes are integrated with the new method that combines RSGWPT and EEMD to extract the crucial characteristics from the measured signal for identifying the running state of rolling element bearings, IMF energy ratio is an effective feature index in fault identification for non-stationary vibration signals, the simulated results have shown that the method is effective for detecting instantaneous frequencies. The feature matrix is formed by modified IMFs and SVD is used to decompose the matrix to obtain the singular value as eigenvector. After the hyper parameters of LSSVM are optimized by PSO algorithm, LSSVM network has faster convergence rate and higher accuracy of classification compared with the traditional methods. And the obtained eigenvector is input to the trained LSSVM- PSO to specify the bearing condition. The proposed method has been successfully applied to fault identification of rolling bearings and the application demonstrates that the faults can be accurately and automatically identified.
References
-
Zhang X., Zhou J. Multi-fault diagnosis for rolling element bearings based on ensemble empirical mode decomposition and optimized support vector machines. Mechanical Systems and Signal Processing, Vol. 41, Issue 1, 2013, p. 127-140.
-
Sui W., Osman S., Wang W. An adaptive envelope spectrum technique for bearing fault detection. Measurement Science and Technology, Vol. 25, Issue 9, 2014, p. 095004.
-
Jiang F., Zhu Z., Li W., et al. Robust condition monitoring and fault diagnosis of rolling element bearings using improved EEMD and statistical features. Measurement Science and Technology, Vol. 25, Issue 2, 2014, p. 025003.
-
Lei Y., Lin J., He Z., et al. Application of an improved kurtogram method for fault diagnosis of rolling element bearings. Mechanical Systems and Signal Processing, Vol. 25, Issue 5, 2011, p. 1738-1749.
-
Liu X., Bo L., He X., et al. Application of correlation matching for automatic bearing fault diagnosis. Journal of Sound and Vibration, Vol. 331, Issue 26, 2012, p. 5838-5852.
-
Muruganatham B., Sanjith M. A., Krishnakumar B., et al. Roller element bearing fault diagnosis using singular spectrum analysis. Mechanical Systems and Signal Processing, Vol. 35, Issue 1, 2013, p. 150-166.
-
Wang W., Lee H. An energy kurtosis demodulation technique for signal denoising and bearing fault detection. Measurement Science and Technology, Vol. 24, Issue 2, 2013, p. 025601.
-
Samanta B., Al-Balushi K. R. Artificial neural network based fault diagnostics of rolling element bearings using time-domain features. Mechanical Systems and Signal Processing, Vol. 17, Issue 2, 2003, p. 317-328.
-
Peng Z. K., Chu F. L. Application of wavelet transform in machine condition monitoring and fault diagnostics: a review with bibliography. Mechanical Systems and Signal Processing, Vol. 18, Issue 2, 2004, p. 199-221.
-
Zhou R., Bao W., Li N., et al. Mechanical equipment fault diagnosis based on redundant second generation wavelet packet transform. Digital Signal Processing, Vol. 20, Issue 1, 2010, p. 276-288.
-
Li N., Zhou R., Hu Q., Liu X. Mechanical fault diagnosis based on redundant second generation wavelet packet transform, neighborhood rough set and support vector machine. Mechanical Systems and Signal Processing, Vol. 28, 2012, p. 608-621.
-
Li Z., He Z. J., Zi Y. Y., Chen X. F. Bearing condition monitoring based on shock pulse method and improved redundant lifting scheme. Mathematics and Computers in Simulation, Vol. 7, Issue 3, 2008, p. 318-338.
-
Bao W., Zhou R., Yang J. G., et al. Anti-aliasing lifting scheme for mechanical vibration fault feature extraction. Mechanical Systems and Signal Processing, Vol. 23, Issue 5, 2009, p. 1458-1473.
-
Huang N. E., Shen Z., et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, Vol. 454, Issue 1971, 1998, p. 903-995.
-
Yang W., Tavner P. J. Empirical mode decomposition, an adaptive approach for interpreting shaft vibratory signals of large rotating machinery. Journal of Sound and Vibration, Vol. 321, Issue 3, 1998, p. 1144-1170.
-
Wu Z., Huang N. E. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Advances in Adaptive Data Analysis, Vol. 1, Issue 1, 2009, p. 1-41.
-
Samanta B., Al-Balushi K. R. Artificial neural network based fault diagnostics of rolling element bearings using time-domain features. Mechanical Systems and Signal Processing, Vol. 17, Issue 2, 2003, p. 317-328.
-
Samanta B., Al-Balushi K. R., Al-Araimi S. A. Artificial neural networks and support vector machines with genetic algorithm for bearing fault detection. Engineering Applications of Artificial Intelligence, Vol. 16, Issue 7, 2003, p. 657-665.
-
Vapnik V. N. The Nature of Statistical Learning Theory. Springer-Verlag, New York, 1995.
-
Kim H. C., Pang S., Je H. M., Kim D., Bang S. Y. Constructing support vector machine ensemble. Pattern Recognition, Vol. 36, Issue 12, 2003, p. 2757-2767.
-
Xu H., Chen G. An intelligent fault identification method of rolling bearings based on LSSVM optimized by improved PSO. Mechanical Systems and Signal Processing, Vol. 35, Issue 1, 2013, p. 167-175.
-
Peng Z., Tse W., Chu F. An improved Hilbert-Huang transform and its application in vibration signal analysis. Journal of Sound and Vibration, Vol. 286, 2005, p. 187-205.
-
Law L. S., Kim J. H., Liew W. Y., Lee S. K. An approach based on wavelet packet decomposition and Hilbert-Huang transform (WPD-HHT) for spindle bearings condition monitoring. Mechanical Systems and Signal Processing, Vol. 33, 2012, p. 197-211.
-
Guo S., Gu G. C., Li C. Y. An algorithm for improving Hilbert-Huang transform. Proceedings of the ICCS. Vol. 3, 2007, p. 137-140.
-
http://csegroups.case.edu/bearingdatacenter.
-
Cheng J. S., Yu D. J., Tang J. S., Yang Y. Application of SVM and SVD technique based on EMD to the fault diagnosis of the rotating machinery. Shock and Vibration, Vol. 16, Issue 1, 2009, p. 89-98.
-
Wu X. J., Huang Q., Zhu X. J. Thermal modeling of a solid oxide fuel cell and micro gas turbine hybrid power system based on modified LS-SVM. International Journal of Hydrogen Energy, Vol. 36, Issue 1, 2011, p. 885-892.
-
Jiang H., He Y., Yao P. Incipient defect identification in rolling bearings using adaptive lifting scheme packet. Journal of Vibroengineering, Vol. 14, Issue 2, 2012, p. 771-782.
-
Zhao X. Z., Ye B. Y. Selection of effective singular values using difference spectrum and its application to fault diagnosis of headstock. Mechanical Systems and Signal Processing, Vol. 25, Issue 5, 2010, p. 1617-1631.
About this article
This study was supported by State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (Grant No. LAPS15019), the Fundamental Research Foundations for the Central Universities (Grant No. 2014JBZ017) and the National Science Foundation of China (Grant No. 51577007).
