Abstract
Based on the rain-flow counting method, a new random numerical simulation method for evaluating dynamic response characteristics of a launch and recovery system is presented in this study. It takes a random irregular wave as an input, and the random distribution characteristics of the dynamic responses of the launch and recovery system of a seafloor drill is analyzed by using the rain-flow counting method. The nonlinear coupling mechanisms among the movements of the ship, the umbilical cable, and the seafloor drill caused by random irregular wave are investigated. A dynamic model that considers the influence of the seawater resistance on the launch and recovery system of seafloor drill is established. Then, significant wave heights are used to produce excitation of the random irregular wave, and the corresponding dynamic random responses of the launch and recovery system are calculated and analyzed. At the same time, the movement of the seafloor drill and the tension of the umbilical cable are calculated and analyzed for the cases of seafloor drill at different water depths. This method provides a new tool for evaluating the dynamic response characteristics of launch and recovery system of other seafloor equipment under random irregular wave.
1. Introduction
Hoisting machinery is widely used to transfer cargo and other equipment from and to various locations in industrial field, such as land hoisting machinery and marine hoisting machinery. Compared to land hoisting machinery, marine hoisting machinery is more complicated due to the influence of many factors, like wave, wind, and ocean currents, which typically impose a greater impact on safety and efficiency of the hoisting operations. Recently, a number of studies involving the dynamic response characteristics among the movement of the ship, the cable, and the cargo of the marine hoisting machinery have been reported in the literature [1-6]. However, in most of these studies, the cargo is not in touch with the seawater and its lifting height is normally from ten to several hundred meters in the process of the hoisting. In order to conduct marine geologic survey, marine environment exploration and other marine scientific investigation, some deep-sea equipment, such as seafloor drill, deep-sea mining vehicle and remote operated vehicle (ROV), requires to be operated near seafloor with different water depths (sometimes, the water depth is more than thousands of meters). Due to the combined effects of wave, wind, and ocean currents, the ship motions are complicated. As a result, when the deep-sea equipment reaches the seafloor, its actual touchdown location may be quite different than the expected one. In addition, the movement of deep-sea equipment will lead to a significant vibration of the cable and make the cable fracture and failure [7-9].
In most studies, regular wave is typically chosen as an external excitation to analyze the dynamic responses of the marine hoisting machinery system. However, this is not true for the actual hoisting operation environment. Actually, real ocean waves are random and irregular, and these wave patterns are constituted by a series of random wavelengths and random wave amplitudes. Based on the statistical analysis of a large amount of random irregular wave patterns, all of them actually have some statistical regularities. For different random irregular wave patterns, the significant wave height could be considered as a statistical characteristic value. Furthermore, in most previous research, the random irregular wave followed the normal distribution, and the significant wave height of the random irregular wave followed the Rayleigh distribution.
In this paper, based on the rain-flow counting method, a new random numerical simulation method is applied to assess dynamic response characteristics of the launch and recovery system. A random wave is used as an input, and the random distribution of dynamic responses of the launch and recovery system are calculated and analyzed. Analysis results can provide theoretical guidance for the estimation of heave compensation and the constant-tension control of the umbilical cable. In addition, random irregular wave was typically chosen as an external excitation to analyze the dynamic responses of the launch and recovery system in this study. We just presented the dynamic response characteristics of the launch and recovery system and the statistic distributed regularity of the responses of the movement of the ship, the umbilical cable, and the seafloor drill in the sea state 4 condition. It is a practical trial to apply statistics analysis to evaluate the dynamic responses of the marine hoisting machinery under random irregular wave.
2. Dynamical model of launch and recovery system
2.1. Model description
Fig. 1 shows a sketch of a launch and recovery system with a seafloor drill. This system mainly includes a ship, a marine winch, an umbilical cable, a hoist boom, and a seafloor drill. Two assumptions are applied for the following analysis in this study:
(1) The elastic deformation of the umbilical cable and the rotation of the seafloor drill are ignored.
(2) The hoist boom is assumed as a rigid rod.
Fig. 1Sketch of launch and recovery system of seafloor drill
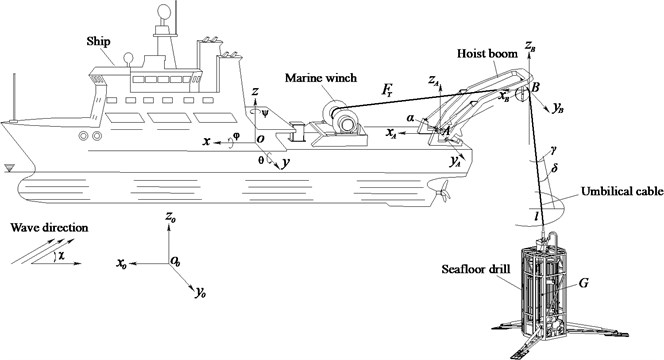
In Fig. 1 three coordinate systems are introduced to describe the launch and recovery system of the seafloor drill. The inertial coordinate system, -, is fixed to the ground. The coordinate system of the ship, -, is fixed to and moves with the ship. Point is located at the center of the rotation axis of the hoist boom, and point is located at the hoisting point of the hoist boom. The distance from point to the origin of the coordinate system of the ship is defined as , and the distance from point to point is defined as . is the angle anticlockwise from to the axis .
In order to describe the orientation of the umbilical cable in -, two angles, represented by and are used (Fig. 1). These two angles will be referred to as the in-plane pendulum angle and the out-of-plane pendulum angle, respectively.
2.2. Ship motions and external loads
The differential equations of heaving, rolling, and pitching motions of the ship caused by irregular waves can be described as follows [10]:
where is the mass of the ship, is the added mass due to heaving motion, , , , and are hydrodynamic coefficients of the heaving motion. and are inertia moment and the additional inertia moment due to the rolling motion, respectively. is the damping moment coefficient of the rolling motion, and are restore moment coefficients of the rolling motion. and are inertia moment and the additional inertia moment due to the pitching motion. , , , and are hydrodynamic coefficients of the pitching motion. , and are the interference forces of the heaving motion, interference moments of the rolling and the pitching motion, respectively. Some coefficients in Eq. (1) could be calculated based on empirical equations [11, 12].
In -, the hydrodynamic pressure at position (, , ) can be expressed as:
where is the density of seawater, is the gravity constant, is the wave number, is the wave surface coordinate.
Based on the Froude-Krylov assumption, the interference force of heaving motion, interference moments of rolling motion and pitching motion can be described as follows:
Substituting Eq. (2) into Eq. (3), and the ship was simplified as a box structure, one has:
where , , and are breadth, draught, and length of the ship, respectively. is the forward speed in the direction of the ship, is the vertical coordinate of the ship’s buoyancy center.
2.3. Dynamic equation of launch and recovery system
The homogeneous transformation matrix from - to - is:
Consequently, the hoisting point of the hoist boom in - can be described as following:
The center of gravity of the seafloor drill is derived as following:
where , , , and are the parameters depended on time, is the length of the umbilical cable, is assumed to be constant. By differentiating the position of the center of gravity of the seafloor drill , the velocity is derived from Eq. (7):
The kinetic energy of the launch and recovery system can be obtained as follows:
where is the mass of the seafloor drill.
The potential energy of the launch and recovery system is obtained:
The Lagrangian function of the launch and recovery system can be expressed as:
The Lagrange equation is:
where , and are general coordinates, general velocities and general forces of the launch and recovery system, respectively.
Substituting Eq. (11) into Eq. (12), one has:
The generalized force of the launch and recovery system is mainly the seawater resistance, it can be expressed as:
where is the density of seawater. , and are resistance coefficients of the movement of the seafloor drill in three directions, and , and are resistance surface areas of seafloor drill in three directions, respectively.
2.4. The tension of umbilical cable
According to Newton’s second law, the movement of the seafloor drill can be expressed as:
where is the tension of the umbilical cable, is the volume of the seafloor drill.
Based on Eq. (17), the tension of the umbilical cable can be expressed as:
3. Dynamic random numerical simulation method
3.1. Random irregular wave model
The random irregular wave is assumed as a superposition of a series of linear waves [13-15]. The wave coordinate of the random irregular wave can be expressed as:
where , and are the wave amplitude, frequency and wave number for wave component , respectively. is the random phase angle of the wave component with uniform distribution between 0 and 2, is the wave angle from the wave direction to the negative direction of the axis .
Wave spectrum is statistic information of random irregular wave and the relationship between wave amplitude and can be written as:
Then Eq. (19) can be expressed as:
Here, a Pierson-Moscowitz (P-M) wave spectrum is selected to describe the wave spectrum [16]. The P-M wave spectrum is defined as:
where is the significant wave height.
Theoretically, the frequency range of P-M wave spectrum is from zero to infinity, but random irregular wave is a stationary stochastic process that belongs to narrow-band spectrum, and its energy mainly concentrated on a narrow frequency band. Therefore, during the numerical simulation process of random irregular wave, the maximum and minimum frequencies and are chosen, and the frequency range from to is discretized through adopting uniformly space sampling. This method not only can guarantee enough accuracy of numerical simulation, but also can significantly improve the efficiency of numerical simulation.
3.2. Significant wave height of random irregular wave
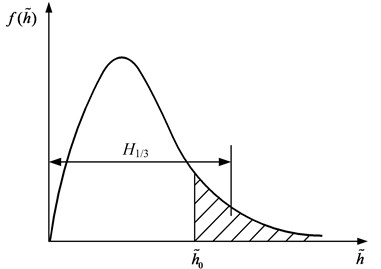
Different sea-states could be represented by different significant wave heights. For example, the significant wave height of sea-state 4 is 2.1 m. In physical oceanography, the significant wave height (illustrated in Fig. 2) is defined, traditionally, as the mean wave height of the highest third of the waves. In Fig. 2, is defined as the significant wave height.
For the continuous density function of the wave height, the significant wave height can be expressed as:
where is the density function of wave height, is the dividing point, and satisfy the following expression:
Fig. 2The definition of significant wave height
Firstly, based on computer-based simulation, an expected value of significant wave height () for a given sea-state is applied to generate a series of random irregular wave. Then, after classifying and analyzing the wave height, the mean wave height of the highest third of the random irregular wave for component could be calculated. Theoretically, when the simulation time approaches infinity, the will approach the given value of significant wave height (). However, typically it will consume quite long simulation time. Therefore, in this paper, we define a terminal condition to stop the numerical simulation:
Given a steady-state deviation , when the deviation between the mean wave height of the highest third of the random irregular wave and the given value of significant wave height () is less than the given steady-state deviation for 10 times continuously, the numerical simulation will stop, and the corresponding wave coordinate is taken as the wave coordinate of the significant wave height of the given sea-state. The terminal condition can be expressed as:
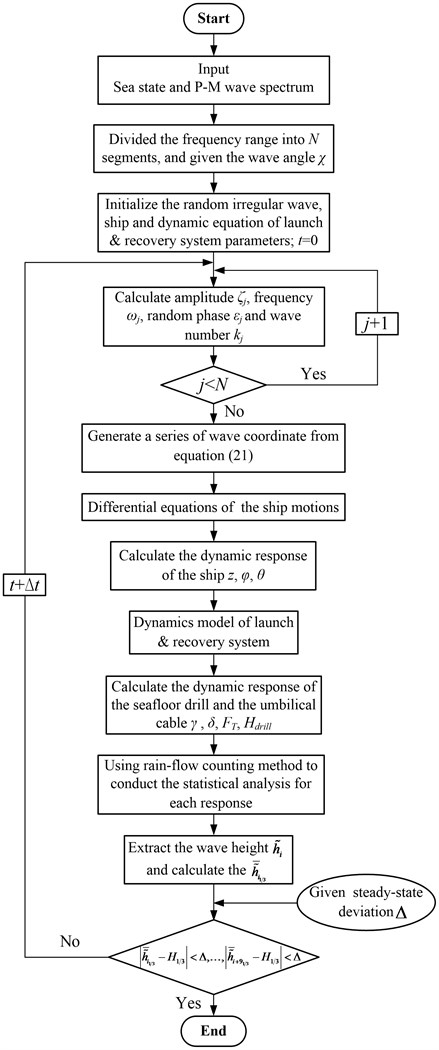
3.3. Dynamic random numerical simulation program
Step 1. Input an expected value of significant wave height () for a given sea-state, and the corresponding P-M wave spectrum.
Step 2. Divide the frequency range (-) into segments, and specify the wave angle .
Step 3. Initialize the random irregular wave, the dynamic equation of launch and recovery system parameters and the simulation time 0.
Step 4. Calculate wave amplitude , wave frequency , random phase andwave number .
Step 5. Apply , ,, and to the wave coordinate Eq. (21) to generate wave coordinate.
Step 6. Calculate the dynamic responses of the ship (heaving motion , rolling motion and pitching motion ) from ship motion equations.
Step 7. Calculate the dynamic responses of the seafloor drill and the umbilical cable (in-plane angle , out-of-plane angle , tension of the umbilical cable , and heaving motion of the seafloor drill ) from Eqs. (13) to (18).
Step 8. Use rain-flow counting method [17-19] to analyze wave coordinate of the random irregular wave, the dynamic responses of the ship, the seafloor drill and the umbilical cable; calculate their statistical distribution and characteristic values.
Step 9. Extract the wave heights of the random irregular wave , , , …, in descending order; then, calculate the mean wave height of the highest third of them.
Step 10. Specify a steady-state deviation as a terminal condition for the numerical simulation, when the following conditions are reached, the numerical simulation will stop, and the corresponding wave coordinate is taken as the wave coordinate of the significant wave height of the given sea-state:
Step 11. If the terminal condition is not satisfied, then ( is the time step of numerical simulation) will come back to Step 4 to continue generate the random irregular wave until satisfy the simulation terminal condition.
Fig. 3 shows the flow chart of the dynamic random numerical simulation of the launch and recovery system.
4. Random numerical simulation of the launch and recovery system
Based on the procedure discussed in the previous section, a calculation case of a scientific research ship under sea-state 4 is demonstrated in this section. The simulation parameters of launch and recovery system are given in Table 1.
Table 1Simulation parameters
Parameters | Values |
Ship length (m) | 73.3 |
Ship breadth (m) | 10.2 |
Ship draught (m) | 3.4 |
Ship mass (kg) | 1200000 |
(m) | 35.5 |
(m) | 6 |
Angle (°) | 135 |
Vertical coordinate (m) | 0.62 |
Seafloor drill mass (kg) | 8000 |
Seafloor drill volume (m3) | 1.56 |
Resistance coefficient | 1.67 |
Resistance coefficient | 1.67 |
Resistance coefficient | 1.67 |
Resistance surface areas | 8.35 |
Resistance surface areas | 8.5 |
Resistance surface areas | 4.67 |
Density of water (kg/m3) | 1000 |
In the process of launch and recovery of the seafloor drill, the ship has been anchored, so we let the forward speed 0.
Fig. 3Flow chart of the dynamic random numerical simulation of the launch and recovery system
4.1. Random irregular wave generation
The significant wave height of sea-state 4 is specified to 2.1 m. The steady-state deviation is 0.001 m. The frequency range from to is (0.3-3) rad/s. The wave direction is 30°, and is 30. The time step of simulation is set to be 0.2 seconds. The convergence of the wave heights of the random irregular wave to 2.1 m is shown in Fig. 4. The total simulation time to achieve this is 35008 seconds.
Fig. 4The convergence of the wave heights of the random irregular wave to 2.1 m
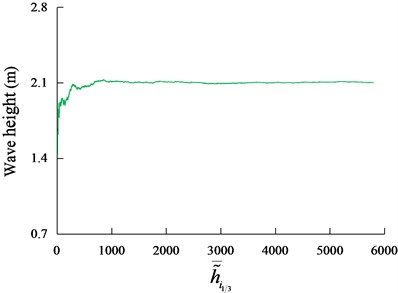
Fig. 5(a) shows a part of the wave coordinate of a random irregular wave. Based on the rain-flow counting method, it can be seen that the wave coordinate of the random irregular wave follows the normal distribution with mean 0.0078 and standard deviation 0.847. The probability density function of the wave coordinate is shown in Fig. 5(a).
Fig. 5The dynamic response of the wave coordinate
a) A part of the wave coordinate of the random irregular wave
b) The probability density function of the wave coordinate
4.2. The dynamic response of the ship
Fig. 6(a) shows a part of the dynamic response of the ship heaving motion. Based on the rain-flow counting method, it can be seen that the ship appeared an irregular heaving motion under this random irregular wave. The ship heaving motion follows the normal distribution with 0.00001 and 0.3479. The probability density function of the ship heaving motion is shown in Fig. 6(b).
Fig. 6The dynamic response of the ship heaving motion
a) A part of the response curve of the ship heaving motion
b) The probability density function of the ship heaving motion
Similarly, the dynamic response data of the ship rolling motion and the ship pitching motion can be obtained by using the rain-flow counting method. The ship rolling motion also follows the normal distribution with 0.0003 and 1.1245. The ship pitching motion follows the normal distribution with 0.00009 and 0.0248.
Compared the dynamic response data of the ship rolling motion with that of the ship pitching motion, it can be found that the standard deviation of the ship rolling motion is larger than the standard deviation of the ship pitching motion, and this is due to the length of the ship is larger than the width of the ship, which makes the pitching motion is more stable than the rolling motion.
4.3. The dynamic response of the seafloor drill and the umbilical cable
Figs. 7(a)-(d) show a part of the dynamic responses of the in-plane, out-of-plane pendulum angle ( and ), the tension of the umbilical cable (), and the heaving motion of the seafloor drill () for the seafloor drill at the depth of 10 m, respectively. Based on the rain-flow counting method, it can be seen that the distribution of the angle , the angle , the and the for the seafloor drill at the depth of 10 m follow normal distributions with –0.0149° and 1.7117; 0.1792° and 8.3203; 67237.9 N, and 30115.8; 0.0980 m, and 0.3674, respectively.
Figs. 8(a)-(d) show the probability density functions of the angle , the angle , the and the for the seafloor drill at the depth of 10 m, respectively.
4.4. The dynamic response of the seafloor drill and the umbilical cable under different water depths
The mean values and the standard deviations of the angle , the angle , the and the for the seafloor drill at the depth of 10 m, 100 m and 1000 m are listed in Table 2.
Fig. 7A part of the dynamic response of the seafloor drill and the umbilical cable for the seafloor drill at the depth of 10 meters
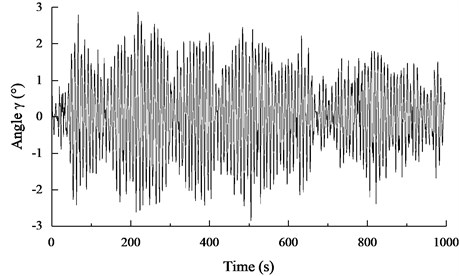
a) A part of the response curve of the pendulum angle
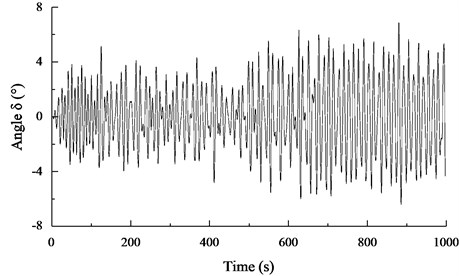
b) A part of the response curve of the pendulum angle
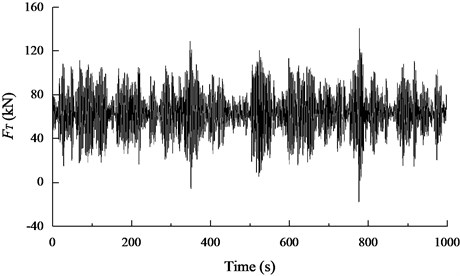
c) A part of the response curve of the tension of the umbilical cable
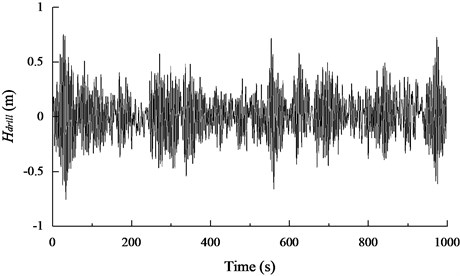
d) A part of the response curve of the heaving motion of the seafloor drill
Fig. 8The probability density function of the of the seafloor drill and the umbilical cable for the seafloor drill at the depth of 10 meter
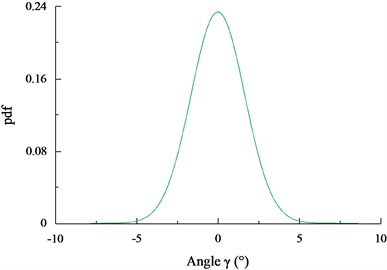
a) The probability density function of the pendulum angle
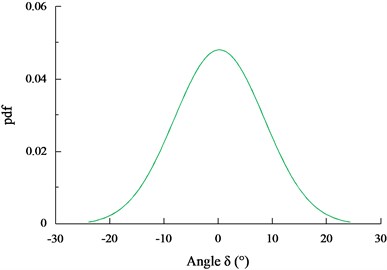
b) The probability density function of the pendulum angle
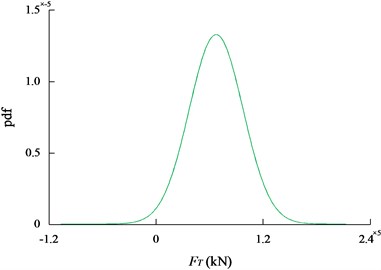
c) The probability density function of the tension of the umbilical cable
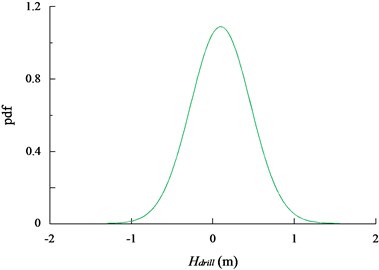
d) The probability density function of the heaving motion of the seafloor drill
Table 2The dynamic response of the seafloor drill and the umbilical cable under different water depths
Water depth 10 m | Water depth 100 m | Water depth 1000 m | ||||
Mean | Standard deviation | Mean | Standard deviation | Mean | Standard deviation | |
Angle (°) | –0.0149 | 1.7117 | 0.0097 | 0.1636 | 0.0005 | 0.0783 |
Angle (°) | 0.1792 | 8.3203 | –0.0807 | 3.1106 | –0.0079 | 0.2113 |
(kN) | 67237.9 | 30115.8 | 67266.1 | 30462.4 | 66865.2 | 31099.6 |
(m) | 0.0980 | 0.3674 | 0.0886 | 0.3616 | 0.0055 | 0.3482 |
By comparing the mean values and the standard deviations of the angle , the angle , the and the at the different depths, it could be concluded that the increase of the water depth will decrease the amplitude of the angle , the angle . the change of water depth does not significantly affect the variation of and . Compared with the standard deviation of the heaving motion of the ship, the standard deviation of the heaving motion of the seafloor drill is more than times larger than it for the seafloor drill at water depth 10 meters, 100 meters and 1000 meters. This is due to the hoist boom was fixed in the quarter-deck of the ship, which make the pitching motion of the ship has the most significant influence on the heaving motion of the seafloor drill.
5. Conclusions
In the current study, a dynamic model that considers the influence of the seawater resistance on the launch and recovery system of a seafloor drill is established. By applying a random irregular wave as an external excitation, the random distribution characteristics of the dynamic responses of the launch and recovery system are analyzed and calculated by using the rain-flow counting method. This study shows that the ship appeared irregular heaving, rolling and pitching motion under random irregular wave, and the ship heaving, rolling and pitching motions follow normal distributions. The increase of the water depth will decrease the amplitude of the in-plane and the out-of-plane pendulum angles. This method provides a new tool for evaluating the dynamic response characteristics of the launch and recovery system of other seafloor equipment under random irregular wave. Analysis results can provide theoretical guidance for the estimation of heave compensation and the constant-tension control of the umbilical cable. In order to more accurately analyze the dynamic response of the launch and recovery system, the elastic deformation of the umbilical cable should be deeply considered and discussed in future study.
References
-
Hama S. H., Roh M. I., Lee H., Ha S. Multibody dynamic analysis of a heavy load suspended by a floating crane with constraint-based wire rope. Ocean Engineering, Vol. 109, 2015, p. 145-160.
-
Schaub H. Rate-based ship-mounted crane payload pendulation control system. Control Engineering Practice, Vol. 16, 2008, p. 132-145.
-
Ismail R. M. T. R., That N. D., Ha Q. P. Modelling and robust trajectory following for offshore container crane systems. Automation in Construction, Vol. 59, 2015, p. 179-187.
-
Ellermann K., Kreuzer E. Nonlinear dynamics in the motion of floating cranes. Multibody System Dynamics, Vol. 9, 2003, p. 377-387.
-
Ran H. L., Wang X. L., Hu Y. J., et al. Dynamic response analysis of moored crane-ship with flexible booms. Journal of Mechanical Engineering, Vol. 45, Issue 10, 2009, p. 42-46.
-
Ku N., Ha S. Dynamic response analysis of heavy load lifting operation in shipyard using multi-cranes. Ocean Engineering, Vol. 83, 2014, p. 63-75.
-
Masoud Z. N., Nayfeh A., Mook D. T. Cargo pendulation reduction of ship-mounted cranes. Nonlinear Dynamics, Vol. 35, 2004, p. 299-311.
-
Wang P. C., Fang Y. C., Xiang J. L., et al. Dynamics analysis and modeling of ship-mounted boom crane. Journal of Mechanical Engineering, Vol. 17, Issue 20, 2011, p. 34-39.
-
Nishi Y. Static analysis of axially moving cables applied for mining nodules on the deep sea floor. Applied Ocean Research, Vol. 34, 2012, p. 45-51.
-
Li J. D. Ship Seakeeping. Harbin Engineering University Press, 2007.
-
Tasai F. Damping Force and added mass of ships heaving and pitching. Transactions of the West Japan Society of Naval Architects, Vol. 21, 1961, p. 109-132.
-
Fossen T. I., Smogeli Ø. N. Nonlinear time-domain strip theory formulation for low-speed manoeuvring and station-keeping. Modeling, Identification and Control, Vol. 25, Issue 4, 2004, p. 201-221.
-
Zelt J. A., Gudmestad O. T., Skjelbreia J. E. Fluid accelerations under irregular waves. Applied Ocean Research, Vol. 17, Issue 1, 1995, p. 43-54.
-
Korde U. A. Near-optimal control of a wave energy device in irregular waves with deterministic-model driven incident wave prediction. Applied Ocean Research, Vol. 53, 2015, p. 31-45.
-
Jeans T. L., Fagley C., Siegel S. G., et al. Irregular deep ocean wave energy attenuation using a cycloidal wave energy converter. International Journal of Marine Energy, Vol. 1, 2013, p. 16-32.
-
Pierson W. J., Moskowitz J. L. A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii. Journal of Geophysical Research, Vol. 69, Issue 24, 1964, p. 5181-5190.
-
Downing S., Socie D. Simple rainflow counting algorithms. International Journal of Fatigue, Vol. 4, Issue 1, 1982, p. 31-40.
-
McInnes C., Meehan P. Equivalence of four-point and three-point rainflow cycle counting algorithms. International Journal of Fatigue, Vol. 30, Issue 3, 2008, p. 547-59.
-
Low Y. M. A simple surrogate model for the rainflow fatigue damage arising from processes with bimodal spectra. Marine Structures, Vol. 38, 2014, p. 72-88.
Cited by
About this article
This work is supported by the National High Technology Research and Development Program of China (“863” Program) (Grant No. 2012AA091301), Science and Technology Project of Hunan Province (Grant No. 2014FJ1004), and the Natural Science Combined Foundation with Province and City of Hunan Province (Grant No. 2015JJ5029).
Data collection: Deshun Liu, Youduo Peng. Data analysis: Buyan Wan, Deshun Liu, Youduo Peng and Zhihua Cai. Data interpretation: Yongping Jin, Buyan Wan and Deshun Liu. Drafting manuscript: Yongping Jin, Buyan Wan, Deshun Liu, Youduo Peng, Zhihua Cai, Jianghui Dong. Revising manuscript: Yongping Jin and Jianghui Dong. All authors have read and approved the final submitted manuscript.
