Abstract
The cavitation flow of axial piston pump was simulated by the FLUENT software. Simulation results show that 1) Plunger cavity cavitation degree increase nearly one time when the piston pump rotation rate increase from 1500 r/min to 3000 r/min; 2) The axial piston pump L shape throttling groove is more conductive to inhibiting cavitation of plunger cavity than the V shape; 3) The variation law which shows the influence of the thickness of cylinder kidney shape port on the cavitation of plunger cavity. This paper put forward the two-way inclined type cylinder barrel kidney shape port, which was beneficial to improve the self-sucking of the plunger cavity under high speed rotation and could inhibit the cavitation of plunger cavity. The Kriging agent model of has been established by taking the configuration parameters of one-way inclined cylinder kidney shape port as independent variables and the mean value of the gas volume fraction of plunger cavity as target function, based on the Kriging interpolation principle. The optimized structure of the one-way inclined type cylinder barrel kidney shape port is obtained through the Kriging agent model which is optimized by using improved genetic algorithm. The structure of the cylinder kidney shape port and the valve plate throttling grooves are obtained, which mostly inhibit the cavitation of plunger cavity with above analysis. The structure has a strong inhibitory on the plunger cavity cavitation through the simulation analysis and verification.
1. Introduction
Axial piston pump which has the advantages of high working pressure, high limit power and convenient variable adjustment, is widely used in the field of industrial hydraulic and walking hydraulic field. In recent years, with the increasing awareness of environmental protection, hydraulic transmission technology with water as the medium has been developed Huazhong University of Science and Technology, Zhejiang University and other institutes have been carried out the research work of the water hydraulic axial piston pump [1, 2].
Along with the development of industry, the working speed and pressure of the axial piston pump becomes higher than before. Compared with the hydraulic oil, water has the characteristics of high saturated vapor pressure and low solubility of air so the plunger cavity water axial piston pump prone to cavitation [3, 4].
At present, many scholars have carried out intensive study on the flow characteristics, pressure impact and cavitation of the axial piston pump, which has achieved some results. Kosodo [5] studied the pressure-flow characteristics and cavitation of hydraulic pump and motor valve plate V groove of the hydraulic system through experiment, and putted forward that the direction of the flow, temperature, pressure and Reynolds coefficient exert greater impact on cavitation. Edge K. A. [6, 7] found that the pressure overshoot of the piston pump is much large than the calculation of the existing theoretical model, and pointed out the model of adding the inertia term of fluid acceleration in the decompression groove. He considered that the large slope triangle groove is conducive to reducing the pressure overshoot. W. Kollek [8] has simulated and studied the piston and cylinder of oblique axial piston pump, and then illustrated that the pump must occurred cavitation in the absorption area. They established the relationship between sound diagnosis signal and the cavitation, and putted forward conception of cavitation in hydraulic system of sound instrument detection. S. Gold [9] built the test platform with organic transparent pipe, and observed the cavitation of the entrance of piston pump by adjusting the inlet pressure and camera technology. The law of the internal pipeline bubble production and development can be clearly observed. Because the pipeline can’t withstand high pressure, the experiment only observed the low pressure zone of axial piston pump entrance. Zhou Hua [10] analyzed the mechanism of cavitation inception and outlet pressure ripple, and carried out the experimental study on cavitation inception characteristics of seawater hydraulic pump. Liu Xiaohong [11] put forward that the cavitation of the valve plate depends on not only the value of velocity and pressure, but also the direction of velocity. She also pointed out that the change of valve plate structure must change the velocity direction to reduce cavitation of the valve plate. ZHAI Jiang [12] have numerically simulated the internal cavitation flow of the water axial piston pump by CFD. Xu Bing [13] compared the flow ripple of axial piston pump with pre-compression volume with the flow ripple of axial piston pump without pre-compression volume by simulation and experimental means. Yuan Shihua [14] studied the dynamic in evolution and effects of gas phase in cavitation of axial piston pump. Shu Wang [15] putted forward that the valve plate design was a critical issue in addressing the cavitation or aeration phenomena in the axial piston pump. N. P. Mandal et al. [16] developed a methodology for designing a swash-plate axial piston pump whose barrel kidney are wider than the bridges separating the kidney ports on the plate. Besides reducing pressure ripples and avoiding cavitation for minimizing the fluid-borne noise, maximization of the pump discharge has also been considered in formulating an objective function to be minimized. S. Kumar et al. [17] put forward that to avoid cavitation, it is important to consider the inclusion of grooves at the piston stroke length and near to the piston pressure side.
Although domestic and foreign scholars have done some research on the axial piston pump cavitation, the literature that includes the impact of the cylinder barrel and valve plate structure of the axial piston pump on the plunger cavity cavitation is less. This paper takes a certain type of the water axial piston pump as research object and analyzes the impact of the cylinder barrel and valve plate structure on cavitation of plunger cavity. The model has taken account the compressibility of the fluid and gas. The content of this paper mainly includes several aspects: 1) Establishment of the finite element simulation model of axial piston pump. 2) Analysis of the impact of cylinder rotation speed on the plunger cavity cavitation. 3) Analysis of ‘V’ and ‘L’ shape throttling groove structure of valve plate influence on the plunger cavity cavitation. 4) Analysis and comparison of ordinary axial piston pump cylinder barrel kidney shape port, one-way incline kidney shape port and two-way incline kidney shape port influence on the plunger cavity cavitation. 5) The Kriging agent model of the structure parameters of one-way incline kidney shape port cylinder and value of gas volume fraction of plunger cavity is established, and the optimized structure is obtained by improved genetic algorithm. 6) The optimization structure of piston pump cylinder and valve plate which can inhibit the cavitation of the plunger cavity to the maximum are put forward according to the former analysis.
2. Establishment of simulation model
2.1. Research object
The research object of this paper is the water axial piston pump. Its structure is shown in Fig. 1. The angle of the swash plate is 15°. The cross angle is 4°. The number of the piston is 9. The piston diameter is 21 mm. Piston distribution circle diameter is 81 mm. Rotation rate is 1500 r/min.
Fig. 1Structural representation of axial piston pump
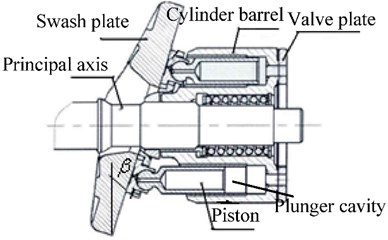
Fig. 2Internal fluid in axial piston pump
2.2. Internal flow channel geometry model of axial piston pump
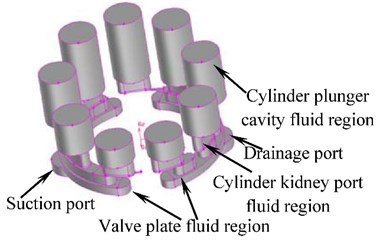
On the premise of no neglect of the leakage of the axial piston pump, the flow channel geometry model of axial piston pump is shown in Fig. 2. In this model, the position of valve plate, suction port and drainage port are fixed. The kidney shape port and plunger cavity rotate with the cylinder, and the volume of the plunger cavity changes with the piston movement. The structure of plunger cavity of axial piston pump, valve plate, and kidney shape port is shown in Fig. 3.
2.3. Mesh division
The axial piston pump is divided by the structure and un-structure grid due to its complex internal flow channel and its changeable size. The mesh is encrypted in small throttling groove, as shown in partial enlargement of Fig. 4. The grid consists of 168813 elements.
2.4. Boundary conditions
As it is shown in Fig. 4, nine plunger cavity of the cylinder barrel is rotated around with the axis, and the movement speed of the piston is expressed as:
The pump inlet and outlet are set as pressure inlet and outlet respectively. The paper determined the values of inlet pressure and outlet pressure as 3.3E5 Pa and 5 MPa respectively. The saturated vapor pressure of water is 2367.8 Pa. The value of the gas volume fraction of pump inlet and outlet is zero. The compressibility of the liquid and gaseous fluid and the piston velocity are set through UDF by using the commercial fluent software and the mixture model, RNG - model, dynamic mesh and sliding mesh. The control equations were space dispersed by finite volume method and non-staggered grid. The two order upwind scheme is adopted in turbulent kinetic energy term. The others adopt the first order upwind scheme. The time dispersion adopts two order full implicit schemes. The SIMPLE algorithm is used in velocity component in momentum equation and pressure coupling problem. Every iterative calculation accuracy is set as 10-8, and time step is set as 10-4.
Fig. 3Valve plate and the plunger cavity structure
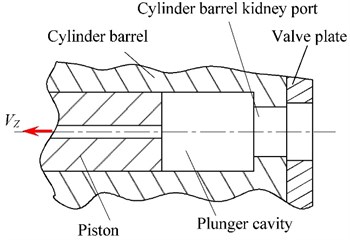
Fig. 4Internal flow channel mesh division of axial piston pump
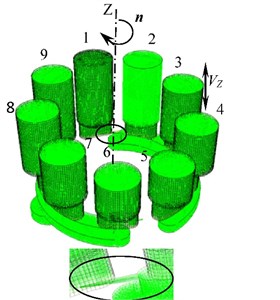
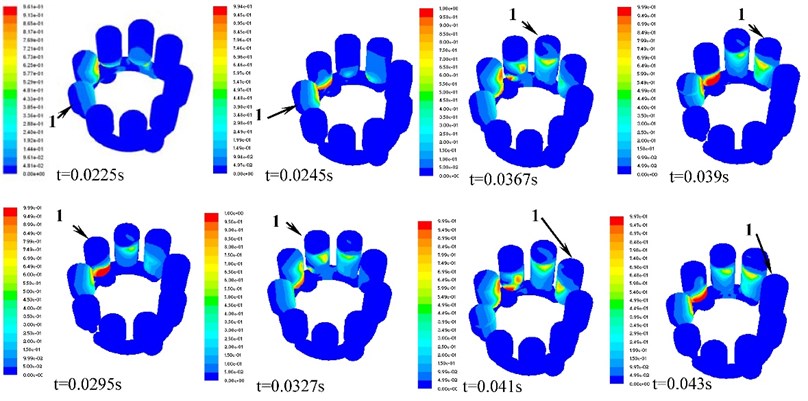
Fig. 5Distribution contours of gas volume fraction of No. 1 plunger cavity
2.5. Cavitation process analysis of plunger cavity
According to the simulation model, the inlet pressure of axial piston pump is 1.01×105 Pa and the outlet pressure is 3.0×106 Pa. The simulation results are shown in Fig. 5. and Fig. 6.
Fig. 5 and Fig. 6 shows that the plunger cavity of water axial piston pump appears the cavitation when the plunger cavity sucks water. Due to the high rotation speed of the plunger cavity, the bubbles in the plunger cavity operated by means of centrifugal force are concentrated in the inner side. When piston cavity drains water, its pressure is high with no cavitation now. When the drainage is over, the plunger cavity passes through the bottom dead centre (BDC) and enters suction port. The pressure of plunger cavity fluid is greater than outlet pressure when the plunger cavity just contacts V shape throttling groove. The fluid in plunger cavity flows backward to outlet in an instant. At this time, the cavitation is not obvious. With the rotation of pump cylinder barrel, the piston moves with variable velocity along the axial, and the plunger cavity pressure drops. The gas in the fluid will precipitate when the fluid pressure in the plunger cavity is lower than the saturated vapor pressure of fluid or air separation pressure of fluid. At this time, the plunger cavity cavitation has been occurrence. The degree of plunger cavity cavitation is little at the beginning and end of drainage period. The degree of plunger cavity cavitation is serious at 0.028 second to 0.03 second this time. The plunger cavity cavitation is most serious especial at 0.0295 second.
Fig. 6Curve chart of mean value of volume fraction of No. 1 plunger cavity
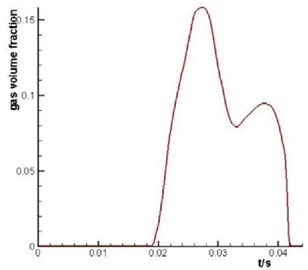
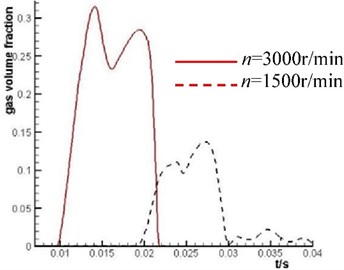
Fig. 7Comparison of the mean value of volume fraction of plunger cavity with different rotating rate
3. Effect of cylinder rotation speed on cavitation of plunger cavity
The inlet pressure of the axial piston pump is 3.03×105 Pa, and the outlet pressure is 5.0×106 Pa. The cylinder barrel rotation rate is 1500 r/min and 3000 r/min. The thickness of cylinder barrel kidney-shape port is 11 millimeters, that is 11 millimeters.
Fig. 7. shows that the gas volume fraction of the fluid in the plunger cavity significantly increases when the pump speed increases. It is indicated that the cavitation degree of the fluid in the plunger cavity increases when the axial piston pump rotation rate increases.
4. Analysis on the influence of valve plate throttling groove structure on the plunger cavity cavitation
4.1. V shaped and L shaped throttling groove flow area and hydraulic radius
Fig. 8 shows geometric sketch map of V and L shape throttling groove.
Calculation formula of the flow area and hydraulic radius of V shape throttling groove is expressed as follows:
Fig. 8Geometric sketch map of V and L shape throttling groove
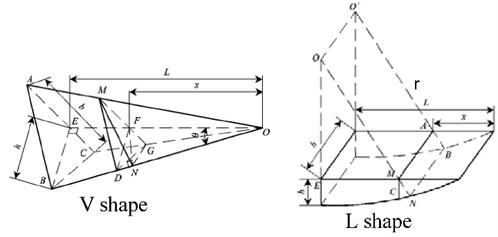
Calculation formula of the flow area and hydraulic radius of L shape throttling groove is express as follows:
The flow area tone-up of V shape throttling groove is very small when the is small, but the flow area tone-up of L shape throttling groove is large when the is smaller. Therefore, high speed axial piston pump with shape throttling groove is more appropriate.
4.2. Effect of V shape and L shape throttling grooves on the plunger cavity cavitation
The simulation analysis of the plunger cavity cavitation is carried out on the axial piston pump with V and L shape throttling groove of valve plate under the rotating speed of 1500 r/min and 3000 r/min. The simulation result is shown in Fig. 9. The high flow tone-up performance of L shape throttling groove is not obvious when the rotation rate of the axial piston pump is low but it is very obvious when the rotation rate of the axial piston pump is high. Because L shape throttling groove has high flow tone-up and the fluid which flow into the plunger cavity is increased, cavitation degree of the plunger cavity decreases significantly.
5. The influence of kidney shape port of cylinder structure on cavitation of plunger cavity
5.1. Kidney shape port of cylinder barrel structure
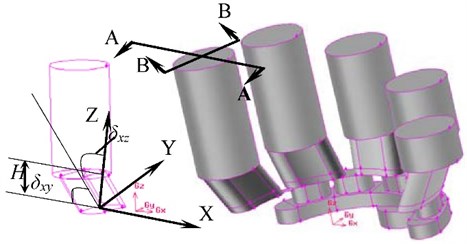
Fig. 10 shows kidney shape port of cylinder barrel structure. The kidney shape port is divided into three types including straight kidney shape, one-way inclined type kidney shape and two-way inclined type kidney shape. Table 1 is the structural parameters of the kidney shape port of cylinder barrel.
5.2. Influence of the inclined type kidney shape port structure of cylinder barrel on self-sucking property
5.2.1. Analysis on the self-sucking property of plunger cavity with
Fig. 11 (A-A view in Fig. 10) shows the one-way inclined kidney-shape port. Because the kidney-shape port inclines certain angle relative to the plane, the fluid in the kidney-shape port is influenced by centrifugal force when the cylinder rotates at high speed.
Fig. 9Comparison of the mean value of gas volume fraction of No. 1 plunger cavity under different rotation rate and different throttling groove
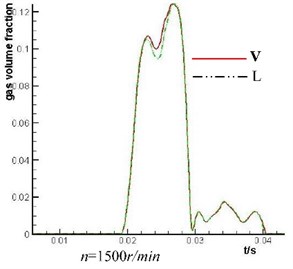
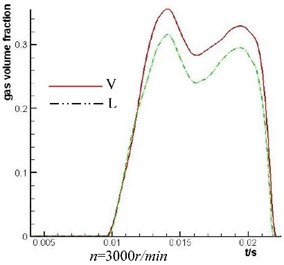
Fig. 10Kidney-shape port structure of cylinder barrel
Fluid press along the path is expressed as:
where is dynamic viscosity, is pipe length, is average flow velocity, is pipe diameter, for non-circular pipe with hydraulic diameter instead of .
Table 1Structural parameters of the cylinder barrel kidney shape port
Kidney shape port of cylinder barrel structure | (°) | (°) | (mm) |
Straight kidney shape | 90 | 0 | 7-15 |
One-way inclined kidney shape | 65-85 | 0 | 7-15 |
Two-way inclined kidney shape | 65-85 | 10-14 | 7-15 |
where is the quality of segment fluid of cylinder kidney-shape port, is centrifugal force of , is the component force of along axis of the cylinder kidney-shape port.
When the cylinder rotates at high speed, the component of centrifugal force of fluid along the axis of cylinder kidney-shape port is expressed as:
where is sectional area of cylinder barrel kidney-shape port.
When is smaller, the centrifugal force of cylinder kidney-shape port fluid and the component force along the axis of cylinder kidney-shape port is higher. Therefore, self-sucking capacity of the plunger cavity is improved. When the height of cylinder kidney-shape port is higher and the is smaller, the length of cylinder kidney-shape port is increased. Meanwhile, loss pressure of fluid along the way is increased and pressure of fluid in the plunger cavity is reduced, which promote the generation of cavitation. So the cavitation degree of plunger cavity is related to the parameter and of cylinder barrel kidney-shape port.
Fig. 11Centrifual force of one-way inclined kidney-shape port of cylinder
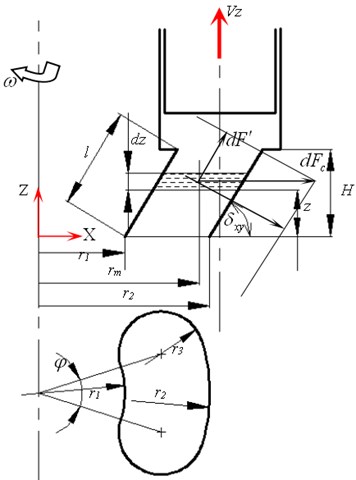
Fig. 12Analysis on the influence of the fluid drainage of the cylinder kidney-shape port on the δxz
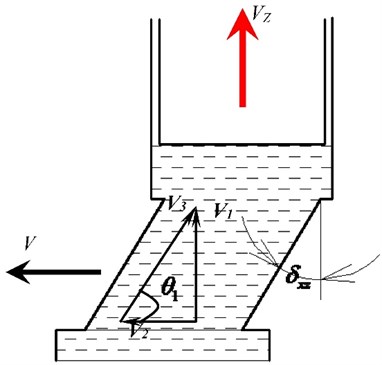
5.2.2. Analysis on the self-sucking property of plunger cavity from
The one-way inclined cylinder kidney-shape port rotate around axis, then the two-way inclined cylinder kidney-shape port is formed. Fig. 12 (B-B view in Fig. 10) shows the influence of on the self-sucking capacity of the plunger cavity.
In Fig. 12 is linear speed, is the tangential velocity of cylinder kidney-shape port fluid, , is the velocity of fluid enter cylinder kidney-shape port, then:
From the seventh formula, the value of the is related to the and the . The value of the is determined by and . is piston movement velocity, and is inlet pressure of axial piston pump. When and 90° – are similar or equal, the fluid in the cylinder kidney-shape port can avoid tangential strong vortex phenomenon, and reduce the flow resistance. Therefore, is changeable when the axial piston pump is working, so also changeable. It is very difficult to makeθ1 and 90° – completely equal.
5.3. Simulation analysis on the influence of the structure of cylinder kidney-shape port on the cavitation of the plunger cavity
Comprehensive the previous analysis, the structure parameters (such as , , ) of cylinder barrel have an effect on the self suction of the plunger cavity. The simulation analysis on the cavitation of the plunger cavity is carried out by using FLUENT software.
5.3.1. Influence of on cavitation of plunger cavity
The simulation analysis on the structure parameters of the cylinder kidney-shape port is described as follows
1) The values of range from 7 to 15 mm.
2) The value of is 85°.
3) The value of is 0°.
4) The value of rotation rate is 3000 r/min.
Fig. 13 shows that the maximum value of the gas volume fraction of the plunger cavity is larger as the value of increases, when the value of ranges from 7 to 15 mm. However, the maximum value of the gas volume fraction of the plunger cavity decreases as the value of increases when the value of exceeds 11 mm. It is because only the value of increases to a certain value as the value of is large that the component of centrifugal force of fluid along the axis of cylinder barrel kidney-shape port can overcome the pressure loss along the side of cylinder barrel kidney-shape port.
Fig. 13Comparison of the mean value of gas volume fraction of No. 1 plunger cavity under different H
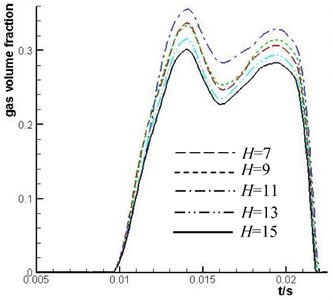
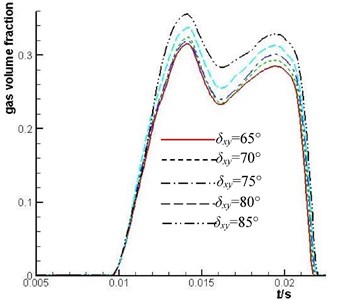
Fig. 14Comparison of the mean value of gas volume fraction of No. 1 plunger cavity under different δxy
5.3.2. Influence of on cavitation of plunger cavity
The simulation analysis on the structure parameters of the cylinder kidney-shape port is described as follows:
1) The value of is 11 mm.
2) The value of range from 65° to 85°.
3) The value of is 0°.
4) The value of rotation rate is 3000 r/min.
Fig. 14 shows that when the gas volume fraction of the plunger cavity becomes smaller, the smaller the is. It is shown that the self-suction of the plunger cavity is enhanced by the centrifugal force of the cylinder barrel kidney-shape port fluid with high rotation and the cavitation of the plunger cavity is inhibited.
5.3.3. Influence of on cavitation of plunger cavity
The simulation analysis on the structure parameters of the cylinder kidney-shape port is described as follows:
1) The value of is 13 mm.
2) The value of is 65°.
3) The values of is 0°, 10°, 12°, 14°.
4) The value of rotation rate is 3000 r/min.
From the curve variation law of Fig. 15, it is found that the value of has obvious effect on cavitation of plunger cavity. The time quantum that ranges from 0.01 second to 0.014 second is the period when the plunger cavity passes through the suction throttling groove. In this period when the value of becomes greater, the gas volume fraction of plunger cavity is greater. Due to the increase of value of , the self suction of the plunger cavity becomes larger. At present the fluid pressure of the valve plate throttle groove drop sharply, and the cavitation is serious which is mainly caused by the small gain of valve plate throttling groove. In order to decrease the cavitation degree at this time, according to the results of the analysis in Section 4.2, the V shape throttling groove can be transformed into L shape throttling groove at high rotation rate.
Fig. 15Comparison of the mean value of gas volume fraction of No. 1 plunger cavity under different δxz
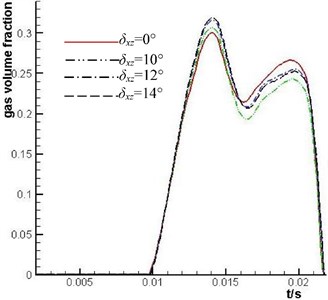
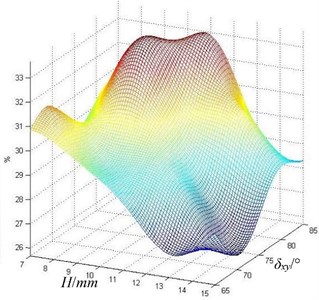
Fig. 16Kriging agent model approximate surface
The time quantum that ranges from 0.01 second to 0.014 second is the period when the plunger cavity has passed through the suction throttling groove. The gas volume fraction of the plunger cavity at this time first decreases rapidly and then increases, which is caused by the rotation rate from being slow to fast. In this period, when is not equal to 0, cavitation of the plunger cavity is more likely to be inhibited than when is equals 0. When the value of is equal to 10°, the increased gradient of the value of gas volume fraction is the smallest after 0.018 second. It is mainly because when the value of is equal to 10°, the and 90° – are best matched. Strong vortex phenomenon is reduced by the fluid in the cylinder kidney hole and the flow resistance is reduced as well.
6. Optimization study on the structure of the one-way inclined cylinder kidney-shape port
6.1. Basic principle of Kriging model
Kriging approximation model is a statistical foresting method which is widely used in mathematical geology based on stochastic processes. It can be used to optimization of regional variable, estimate of linear and unbiased interpolation. It has the statistical characteristics of smoothing effect and estimate of minimum variance. It has played an important role in linear geological statistics [18-20].
The Kriging model assumes that the true relationship between the system response values and the independent variables can be expressed as follows:
where is Kriging unknown model, is Known function (return part) of is Corresponding undetermined parameter, is a deterministic part and called the deterministic drift, is the error of random distribution and is a statistical process. Its mean value is 0 and the variance is not 0.
Take the Gauss function as correlation function (), and that is:
The estimate of Kriging model in the experimental sample point estimate is:
where is sampling points, is the orthogonal correlation function of No. 13, is the Regression constant, is the estimated value of , is the Correlation vector.
The likelihood function of the correlation function is defined as follows:
The least squares estimation of and in the No. 15 formula is:
Thus, and can be determined for a certain sample space. The maximum likelihood method is:
The accuracy of predicted value is determined by the distance between sample points and forecast point . When the sample point is closer to the forecast point , the error of the predicated value is smaller.
6.2. Establishment of Kriging agent model
Through simulation analysis above, it is found that the and 90° – match best when the equals 10°. At this moment, the cavitation degree of the plunger cavity is the smallest. At the same time, and also affect the cavitation of the plunger cavity, but the and have a certain correlation. Therefore, in this paper, the Kriging agent model is established using constant regression model by taking the parameters and as independent variables and the gas volume fraction of plunger cavity as function value when the t equals 0.019 second. In this paper, the five level full factorial experimental design is used. Value of is 7, 9, 11, 13 and 15 mm. Value of is 65°, 70°, 75°, 80° and 85°. The twenty-five structure models have been simulated and analyzed. The Kriging agent model is established by taking Gauss function as correlation function, and is shown in Fig. 16.
6.3. Optimization results of genetic algorithm (GA) and its simulation analysis
6.3.1. Genetic algorithm
GA is global, parallel, stochastic search methods, founded on Darwinian evolutionary principles. During the last decade GA has been applied in a variety of areas, with varying degrees of success within each. A significant contribution has been made in machine engineering. Commonly GA has been used to optimize both structure and parameter values for both controllers and plant models. It has also been applied to fault diagnosis, stability analysis, robot path-planning and combinatorial problems. The proposed genetic algorithm can be performed by the following major steps:
Step 1. Generate the initial population.
Step 2. Calculate the fitness score and select two having the best scores.
Step 3. Perform crossover with rate of and mutation with the rate of , and for reproduction of the new generation using the elitist selection method.
Step 4. Stop when the number of predefined iteration/computational time is reached.
6.3.2. Genetic algorithm operators
Now the genetic algorithm is applied to optimize the agent model. First, genetic operators and other parameters must be defined in the genetic algorithm, namely: population number, crossover with rate, mutation with rate, maximum number of generations (MUG), generation gap and variable interval. The paper determined the values of and as 0.9 and 0.7 respectively. The values of other parameters are shown in Table 2. The optimal solution of the Kriging agent model is shown in Fig. 17.
Table 2The values of other parameters
Parameter | Population number | MUG | Generation gap | (mm) | (°) |
Value | 60 | 400 | 0.9 | 7-15 | 65-85 |
When is 14.87 mm, and is 70.61°, the minimum target value of the gas volume fraction of the plunger cavity is 26.24 %.
Fig. 17The change lines chart of the genetic iterative optimization and calculation
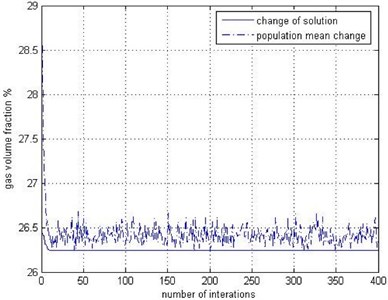
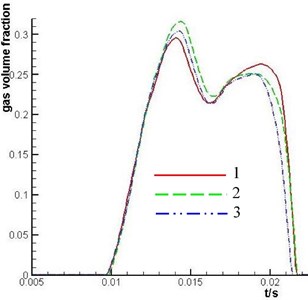
Fig. 18Curve charts of gas volume fraction in piston cavity of optimized structure of axial piston pump
6.4. Establishment of optimization structure of cylinder kidney-shape port of piston pump and its simulation analysis
According to the result of genetic optimization calculation, the main structural parameters of the one-way inclined cylinder kidney-shape port are determined. The value of is 14.87 mm and the value of is 70.61°. Simulation analysis of gas fraction of plunger cavity is shown by curve 1 in Fig. 18.
To further reduce the cavitation degree of plunger cavity, the optimized structure of one-way inclined cylinder kidney-shape port can be transformed into the two-way inclined cylinder kidney-shape port. According to the result of the analysis in section 4.3.3, the value of is 10°, which is determined. Simulation analysis of gas fraction of plunger cavity is shown by curve 2 in Fig. 18.
Comparing curve 2 with curve 1, the cavitation of the plunger cavity has some improvement from 0.016 second to 0.02 second. But in the range of 0.01 second to 0.014 second, the cavitation degree of the plunger cavity increases. The self-suction of the plunger cavity increases, which is mainly because of adopting two-way inclined cylinder kidney-shape port. However, a certain degree of air suction has occurred because the flow gain of the V shape throttling groove is small when the plunger cavity passes through the V shape throttling groove of valve plate. In order to improve the situation, with the analysis of section 4.2, the V shape throttling groove can be replaced by L shape throttling groove. Simulation analysis of gas fraction of plunger cavity is shown by curve 3 in Fig. 18. According to the change regulation of the three curves in Fig. 18, it is obvious that the axial piston pump structure corresponding to the third curve in Fig. 18 has obviously inhibition to the cavitation of the plunger cavity.
7. Conclusions
Through the simulation analysis and research of axial piston pump, the following conclusions have been reached as follows:
1) The cavitation degree in plunger cavity of water axial piston pump increases doubly with the increase of the rotation rate of cylinder.
2) The L shape throttling groove of valve plate has better flow gain the V shape throttling groove and has a certain inhibition for the cavitation of the plunger cavity.
3) The two-way inclined cylinder kidney-shape port can improve the self-suction of plunger cavity and reduce the cavitation of plunger cavity.
4) The approximate function relationship between the gas volume fraction of the plunger cavity and the structural parameters of the one-way inclined cylinder kidney-shape port is established by the Kriging interpolation principle. The strong coupling relationship between the gas volume fraction of the plunger cavity and the structure parameters of axial piston pump is solved. The optimal structure of the two-way inclined cylinder kidney-shape port is obtained through the analysis. The value of main structural parameters of it is shown in Table 3. This structure is best for the cavitation inhibition of the plunger cavity.
Table 3The optimal structural parameters of two-way inclined cylinder kidney shape port
(°) | (°) | (mm) |
70.67 | 10 | 14.87 |
References
-
Norman Bügener, Helduser S. Analysis of the suction performance of axial piston pumps by means of computational fluid dynamics (CFD). The 7th International Fluid Power Conference, Aachen, Germany, 2010.
-
Matthias Heinz, Ridley Fidler, Werner Dittrich, et al. Axial piston pump and motor optimization by means of CFD. The 7th International Fluid Power Conference, Aachen, Germany, 2010.
-
Lim G. H., Chua P. S. K., He Y. B. Modern water hydraulics-the new energy-transmission technology in fluid power. Applied Energy, Vol. 76, Issues 1-3, 2003, p. 239-246.
-
Yang Huayong, Zhou Hua Some key problems of the water hydraulics. Chinese Journal of Mechanical Engineering, Vol. 38, Issue 1, 2002, p. 96-100, (in Chinese).
-
Kosodo H., Nara M., Kakehida S., et al. Experimental research about pressure-flow characteristics of V-notch. Proceedings of the Third JHPS International Symposium on Fluid Power, Yokohama, 1996, p. 73-78.
-
Edge K. A. Cvlinder pressure transients in oil hydraulic pump with sliding plate valves. Proceedings of Institute of Mechanical Engineers, Vol. 200, Issue B1, 1986, p. 45-54.
-
Edge K. A., Darling J. The pumping dynamics of swash plate piston pump. Journal of Dynamic Systems Measurement and Control Transactions of The ASME, Vol. 111, Issue 2, 1989, p. 307-312.
-
Kollek W., Kudzma Z., Stosiak M., Mckiewicz J. Possibilities of diagnosing cavitation in hydraulic systems. Archives of Civil and Mechanical Engineering, Vol. 7, Issue 1, 2007, p. 61-63.
-
Gold S., Helduser S., Wusmann W. Experimental and numerical investigations of suction permanee of pumps. 6th International Fluid Power Conference, TU Dresden, 2008.
-
Zhou Hua, Yang Huayong Cavitation inception of sea water hydraulic pump. Chinese Journal of Mechanical Engineering, Vol. 35, Issue 6, 1999, p. 52-55, (in Chinese).
-
Liu Xiaohong, Yu Lanying, Liu Huanlong, Ke Jian Cavitation erosion mechanism of port plate of hydraulic axial planger pump. Chinese Journal of Mechanical Engineering, Vol. 44, Issue 11, 2008, p. 203-208, (in Chinese).
-
Zhai Jiang, Zhao Yonggang, Zhou Hua Numerical simulation of cavitating flow in water hydraulic axial piston pump. Transactions of the Chinese Society for Agricultural Machinery, Vol. 43, Issue 11, 2012, p. 244-249, (in Chinese).
-
Xu Bing, Song Yuechao, Yang Huayong Pre-compression volume on flow ripple reduction of a piston pump. Chinese Journal of Mechanical Engineering, Vol. 26, Issue 6, 2013, p. 1259-1266.
-
Yuan Shihua, Zhou Junjie, Luo Xianwei Dynamic in evolution and effects of gas phase in cavitation of axial piston pump. ACTA Armamentarii, Vol. 36, Issue 3, 2015, p. 559-565, (in Chinese).
-
Shu Wang The analysis of cavitation problems in the axial piston pump. Journal of Fluids Engineering, Vol. 132, Issue 7, 2010, p. 074502-074507.
-
Mandal N. P., Saha R., Sanyal D. Effects of flow inertia modeling and valve-plate geometry on swash-plate axial-piston pump performance. Proceedings of the Institution of Mechanical Engineering, Part I: Journal of Systems and Control Engineering, Vol. 226, Issue 4, 2012, p. 451-465.
-
Kumar S., Bergada J. M. The effect of piston grooves performance in an axial piston pumps via CFD analysis. International Journal of Mechanical Sciences, Vol. 66, 2013, p. 168-179.
-
Yin Dawei, Li Benwei, Wang Yonghua Aeroengine compressor characteristics metamodeling using kriging method. Acta Aeronautica and Astronautiaca Sincica, Vol. 32, Issue 1, 2011, p. 99-106, (in Chinese).
-
Song X. G., Wang L., Park Y. C. Analysis and optimization of butterfly valve disc. Journal of Process Mechanical Engineering, Vol. 223, Issue 2, 2009, p. 81-89, (in Chinese).
-
Xie Su-chao, Zhou Hui Optimization on passenger compartment structure of railway vehicle based on Kriging method. Journal of Central South University (Science and Technology). Vol. 43, Issue 5, 2012, p. 1190-1198, (in Chinese).
Cited by
About this article
Project supported by the Major National Science and Technology Projects of China (No. 2010ZX04015-011) and by the Science and Technology Project of Sichuan Province of China (No. 2010GZ0093).
