Abstract
In the present study, we perform the nonlinear free vibration analysis of nanobeams under longitudinal magnetic field based on Eringen’s nonlocal elasticity and Euler-Bernoulli beam theory. To capture the small scale effect of the nanobeams, we adopt the nonlocal beam model with the nonlocal parameter. We use the Hamilton’s principle and von-Kármán’s nonlinear strain-displacement relationships to derive the governing equations of nanobeams subject to magnetic field. In order to solve the equations, we utilize the Galerkin method and He’s variational method to come up with an approximate analytical solution for the nonlinear frequency of the nanobeams under magnetic field. In the numerical results, the nonlinear frequency ratio is presented for various values of the dimensionless nonlocal parameter and the dimensionless amplitude. Finally, we investigate the effect of nonlocal parameter on the nonlinear frequency ratio; moreover, we study and discuss the effect of magnetic field on the nonlinear free vibration behavior of nanobeams.
1. Introduction
Carbon nanotubes (CNTs) has attracted worldwide attention due to their potential use in the fields of chemistry, physics, nano-engineering, electrical engineering, materials science, reinforced composite structures and construction engineering. Both experimental and atomistic simulation studies show that when the dimensions of structures become very small, the size effect is important. Due to this fact, the size effect plays an important role on the mechanical behavior of micro- and nanostructures, and it cannot be ignored. Since controlled experiments in nanoscale are both difficult and expensive, the development of appropriate mathematical models for nanostructures is an important issue concerning approximate analysis of nanostructures. The nonlocal elasticity theory, which was introduced by Eringen [1] to account for scale effect in elasticity, was used to study lattice dispersion of elastic waves, wave propagation in composites, dislocation mechanics, fracture mechanics and surface tension fluids. According to the Eringen’s nonlocal elasticity theory, the stress at a reference point is considered to be a function of the strains at all other points in the body. The study of Peddieson et al. [2] can be considered to be a pioneering work which first applied the nonlocal continuum theory to the nanotechnology to obtain the static deformations of beam structures by using a simplified nonlocal beam model based on the nonlocal elasticity theory of Eringen [1]. After this study, a great deal of attention has been focused on studying the static, buckling and vibration [3] analysis of nanostructures. Previous theoretical and experimental studies show that the mechanical behavior of nanostructures is nonlinear in nature when they are subjected to large external loads [4]. It is also known that when a beam with immovable end supports undergoes transverse vibration, an axial tension is produced, which is nonlinearly proportional to the amount of lateral deflection of the beam, and the beam vibrates in the nonlinear regime. Relatively little attention has been paid to the nonlinear analysis of nanostructures. For example, Yang et al. [4] studied nonlinear free vibration of single-walled carbon nanotubes (SWCNTs) based on von-Kármán’s geometric nonlinearity and Eringen’s nonlocal elasticity theory by using differential quadrature method. Ke et al. [5] performed the nonlinear free vibration analysis of double-walled carbon nanotubes (DWCNTs) by considering the nonlocal effect in conjunction with Timoshenko beam theory. More recently, Fang et al. [6] have examined size-dependent nonlinear vibration of DWCNTs by using the harmonic balance method and Davidon-Fletcher-Powell method. The study of nonlinear oscillators, which are described by nonlinear differential equations, is of great importance in areas of engineering, physics and other disciplines. The solution of nonlinear differential equations is more complex and therefore very time consuming. Furthermore, in most cases, the exact solution of the nonlinear equations is not possible, and therefore some approximate solution methods are needed. In this context, significant advances have been made recently in developing various analytical and numerical techniques to solve different type of nonlinear problems in structural mechanics, i.e., the multiple scales method, the elliptic Lindstedt-Poincare method, the harmonic balance method [7], the variational iteration method [8], the homotopy perturbation method [9, 10]. More recently, He [11] has proposed a novel variational method to obtain a simple and efficient approximate closed form solution for nonlinear differential equations. This new method, which is Ritz-like method, can be easily extended to any nonlinear oscillator without any difficulty. For example, Fallah and Aghdam [12, 13] used He’s method to examine nonlinear free vibration of functionally graded beams on nonlinear elastic foundation in the framework of the classical (local) elasticity theory. In the present paper, He’s variational method is applied to nonlinear free vibration of nanobeams subjected to longitudinal magnetic field based on the Eringen’s nonlocal elasticity. The assumption of Eringen’s nonlocal elasticity model is in agreement with the atomic theory of lattice dynamics and experimental observations on phonon dispersion. That is why the results for nanostructures from nonlocal elasticity are better than those from local (classical) elasticity theory. The nonlinearity of the problem is introduced by the axial force due to the stretching. The Hamilton’s principal is adopted to derive the governing equations together with Euler-Bernoulli beam theory and the von-Kármán’s nonlinear strain–displacement relationships. An approximate analytical expression is obtained for the nonlinear frequency of the nanobeam by utilizing the Galerkin method and He’s variational method. Some numerical examples are presented for the nonlinear frequency ratio for nanobeams with longitudinal magnetic field.
2. Governing equation
Based on the Euler-Bernoulli beam theory, the displacement field of any point of the beam is given as:
where and are the axial and the transverse displacement of any point on the neutral axis. The von-Kármán’s nonlinear strain–displacement relationship based on assumptions of large transverse displacements, moderate rotations and small strains for a straight beam are given by:
where is the longitudinal strain, is the nonlinear membrane strain, is the curvature of the beam. In this study, the equations of motion are derived by using Hamilton’s principle. This principle can be expressed as:
where is the kinetic energy, is the strain energy and is the work done by the external applied forces. Based on nonlocal elasticity theory, the nonlocal governing equations in terms of the displacements can be obtained as follows:
where is the Young’s modulus of elasticity, is the area moment of inertia, is the cross section area, defines the mass density and denotes the length of the nano beam respectively; is distributed transverse load, is a constant appropriate to each material, is an internal characteristic length (e.g., length of C-C bond, lattice parameter, and granular distance). Now let us consider the nanobeam is subjected to an externally applied longitudinal magnetic field, then the governing equation of motion of the system can be expressed as follows:
where is the magnetic force per unit length, denotes the Lorentz force in the direction due to longitudinal magnetic field, is the magnetic field permeability and is the longitudinal magnetic field. In order to obtain general results, the following non-dimensional quantities can be defined:
where is the radius of gyration of the cross-section. Using Eq. (9) and neglecting the distributed load for free vibration analysis, the equation of motion can be written in the non-dimensional form as follows:
where , , both and are dimensionless magnetic field intensity. According to the usual Galerkin method, an approximate solution for is assumed as:
where is the unknown time-dependent coefficient to be determined and is the basis function which must satisfy the kinematic boundary conditions.
Substituting the approximate solution in Eq. (11) into Eq. (10), then multiplying both sides of the resulting equation with and integrating it over the domain (0, 1) yields:
Here is the second derivative of with respect to time. The coefficients , and in Eq. (12) can be expressed as:
where is the fourth derivative of with respect to . It should be noted that the midpoint of the nanobeam is subjected to the following initial conditions:
where is the dimensionless maximum vibration amplitude of the nanobeam.
3. Analytical solution based on He’s variational method
By using the semi-inverse method, Eq. (12) can be expressed as:
where is the period of the nonlinear oscillator. When the approximate solution that satisfies the initial conditions in Eq. (14) is considered with the transformation , one can obtain:
The stationary condition results in:
After some amendment, Eq. (17) takes the following form:
The nonlinear natural frequency can be found by performing the integral expression in Eq. (18) as follows:
Then the following approximate solution can be found for :
4. Numerical results and discussion
First of all, nonlinear free vibration of nanobeams without magnetic field is obtained based on the nonlocal elasticity and Euler-Bernoulli beam theory. For comparison with the previously published results, the ratio of nonlinear frequency to linear frequency is presented. It is seen from Eq. (19) that if is set to zero, the linear frequency is obtained, namely . In the light of this information, the nonlinear frequency ratio is expressed as:
Physically, the nonlinear frequency is the frequency of the nonlinear system, which depends on the amplitude of the oscillations as it can be detected from Eq. (21), while for linear system the frequency is independent of the amplitude of the oscillations. In the numerical results, the nonlinear frequency ratio is presented for various values of the dimensionless nonlocal parameter () and the dimensionless amplitude (). In this study, the boundary conditions of the nanobeam are considered as simply supported at both ends. In order to validate the present results, some comparisons with previous studies have been carried out. The formulation and solution method proposed herein is validated against the available results regarding to the nonlinear frequency ratio of beams based on the classical beam theory [12] and [14].
Table 1Comparison of the nonlinear frequency ratio for various values of dimensionless amplitude
Dimensionless amplitude () | Present | Ref. [12] | Ref. [14] |
1 | 1.0897 | 1.0897 | 1.0897 |
2 | 1.3228 | 1.3229 | 1.3228 |
3 | 1.6393 | 1.6393 | 1.6393 |
4 | 2.0000 | 1.9999 | 1.9999 |
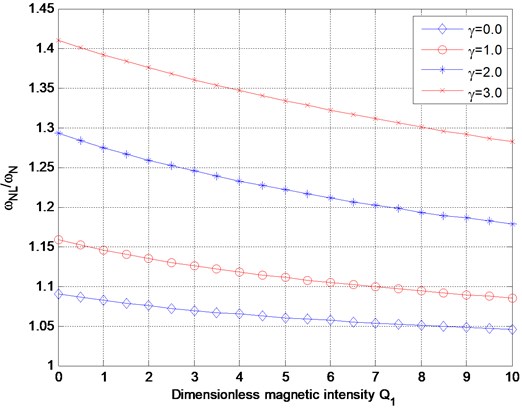
In Table 1, the nonlinear frequency ratio values obtained by the present method are compared with the results of [12] and [14]. According to this table it is observed that the nonlinear frequency ratio values generated from this study agree well with the results from Refs. [12] and [14]. Figs. 1 presents the variation of the nonlinear frequency ratio with the dimensionless amplitude for the selected values of the dimensionless nonlocal parameter (i.e., 0, 0.1, 0.2 and 0.3) without magnetic field or with magnetic field ( 5, 0.1). The figure reveals that the nonlinear frequency ratio increases as the dimensionless amplitude increases. This behavior is known as “hardening spring” behavior. The reason of this behavior is that increasing the dimensionless amplitude implies increasing the axial stretching due to the large deflection, and that leads to a stiffer structure and a larger nonlinear frequency. Furthermore, the nonlinear frequency ratio decreases when the nanobeam is subjected to the magnetic field. Fig. 2 displays the variation of the nonlinear frequency ratio with the dimensionless nonlocal parameter at a given value of the dimensionless amplitude (1). Obviously, the nonlinear frequency ratio increases with the increase of the dimensionless nonlocal parameter, moreover, the nonlinear frequency ratio decreases when the magnetic field intensity increases. Based on the results in Figs. 1-2, it is observed both the dimensionless nonlocal parameter and the dimensionless amplitude cause a rise in the nonlinear frequency. Also, note that the nonlinear frequency is nonlinearly dependent on the dimensionless nonlocal parameter and vibration amplitude. Fig. 3 presents the variation of nonlinear frequency ratio with dimensionless magnetic intensity for various dimensionless nonlocal parameters. As it can be detected from the figures, the nonlinear frequency ratio decreases with the increase of the magnetic field intensity, which is reasonable.
Fig. 1Variation of nonlinear frequency ratio with dimensionless amplitude without magnetic field or with magnetic field
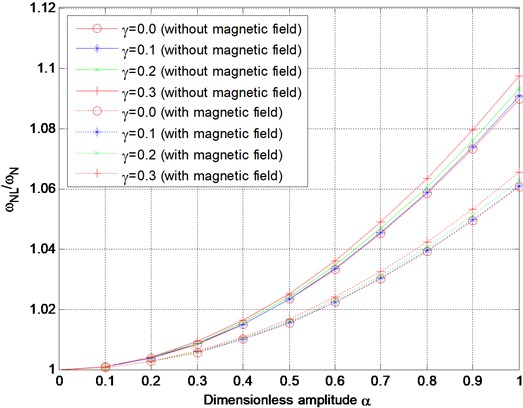
Fig. 2Variation of nonlinear frequency ratio with dimensionless nonlocal parameter without magnetic field or with magnetic field
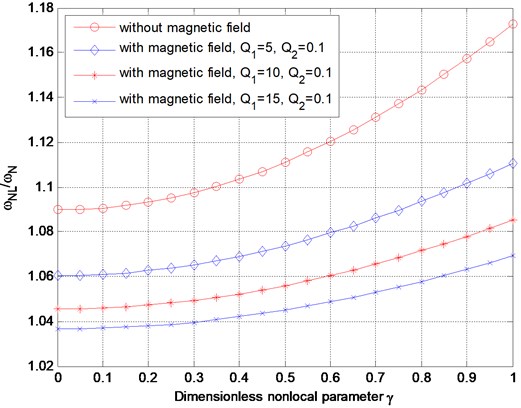
Fig. 3Variation of nonlinear frequency ratio with dimensionless magnetic intensity Q1 for various dimensionless nonlocal parameter
5. Conclusions
Based on the Eringen’s nonlocal elasticity and Euler-Bernoulli beam theory, nonlinear free vibration behavior of the nanobeam under longitudinal magnetic field is studied. The governing equations are derived using the Hamilton’s principal. The von-Kármán’s nonlinear strain-displacement relationships causes the nonlinearity of the problem. In the present study, He’s variational method is adopted to the problem of nonlinear free vibration of nanobeams. An approximate analytical solution is obtained for the nonlinear frequency of the nanobeam by using He’s variational method. The effects of the dimensionless nonlocal parameter on the nonlinear frequency ratio are investigated and discussed. To the best of the author’s knowledge, the present approach is the first work dealing with the complicated problem because the present approach not only studies the nonlinear vibration hehavior of the nanobeam under magnetic field, but also investigates the small scale effects of the nanobeam using nonlocal elasticity theory and uses He’s variational method to obtain the nonlinear frequency of the nanobeam. Numerical results show that the nonlocal effects play an important role on the nonlinear responses of the nanobeams. The new nonlocal beam model produces larger nonlinear frequency ratio than the classical (local) beam model. Therefore, the nonlocal effects should be considered in the analysis of mechanical behavior of nanostructures. Furthermore, it is concluded that the nonlinear frequency ratio of nanobeam with magnetic field decreases with the increase of the magnetic field intensity. The present study only investigates the nanostructure subjected to longitudinal magnetic field, it is interesting to consider the nanostruture subjected to magnetic field in three dimensional directions in the future.
References
-
Eringen A. C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, Vol. 54, 1983, p. 4703–4710.
-
Peddieson J., Buchanan G. R., McNitt R. P. Application of nonlocal continuum models to nanotechnology. International Journal of Engineering Science, Vol. 41, 2003, p. 305-312.
-
Aydogdu M. A general nonlocal beam theory: its application to nanobeam bending, buckling and vibration. Physica E, Vol. 41, 2009, p. 1651-1655.
-
Yang J., Ke L. L., Kitipornchai S. Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory. Physica E, Vol. 42, 2010, p. 1727-1735.
-
Ke L. L., Xiang Y., Yang J., Kitipornchai S. Nonlinear free vibration of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory. Computational Materials Science, Vol. 47, 2009, p. 409-417.
-
Fang B., Zhen Y. X., Zhang C. P., Tang Y. Nonlinear vibration analysis of double-walled carbon nanotubes based on nonlocal elasticity theory. Applied Mathematical Modelling, Vol. 37, 2013, p. 1096-1107.
-
He J. H. Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering, Vol. 178, 1999, p. 257-262.
-
He J. H. Some asymptotic methods for strongly nonlinear equations. International Journal of Modern Physics B, Vol. 20, 2006, p. 1141-1199.
-
Ganji D. D., Sadighi A. Application of He’s homotopy-perturbation method to nonlinear coupled systems of reaction-diffusion equations. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, 2006, p. 411-418.
-
Ozis T., Yildirim A. Traveling wave solution of Korteweg-de Vries equation using He’s homotopy perturbation method. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 8, 2007, p. 239-242.
-
He J. H. Variational approach for nonlinear oscillators. Chaos, Solitons and Fractals, Vol. 34, 2007, p. 1430-1439.
-
Fallah A., Aghdam M. M. Nonlinear free vibration and post-buckling analysis of functionally graded beams on nonlinear elastic foundation. European Journal of Mechanics – A/Solids, Vol. 30, 2011, p. 571-583.
-
Fallah A., Aghdam M. M. Thermo-mechanical buckling and nonlinear free vibration analysis of functionally graded beams on nonlinear elastic foundation. Composites Part B: Engineering, Vol. 43, 2012, p. 1523-1530.
-
Pirbodaghi T., Ahmadian M. T., Fesanghary M. On the homotopy analysis method for non-linear vibration of beams. Mechanics Research Communications, Vol. 36, 2009, p. 143-148.
Cited by
About this article
This research was partially supported by the National Science Council in Taiwan through Grant No. NSC-99-2221-E-327-020. The author is grateful for the financial support.
