Abstract
Wave-based method (WBM), which is derived from indirect Trefftz method, is a new novel deterministic prediction technique for analyzing structural dynamic-response problems in the mid-frequency range. WBM has geometrical limitations, which can be overcome through complement-graph conception by introducing the multi-level modeling theory. To illustrate the feasibility and efficiency of WBM, the dynamic-response process is implemented using a thin-plate structure as a numerical example. The numerical result extends the ability of WBM to deal with the dynamic problem in concave domain.
1. Introduction
Structural-acoustic radiation problems are research hotspot issue in engineering design and manufacturing. The problem over the entire frequency range of interest can be categorized into three groups, i.e., low-frequency, mid-frequency and high-frequency ranges. The distinction among these different frequency ranges is based on the ratio between the free-field wavelength () and the characteristic dimension () of design problem. Numerical calculation method is used as an efficient tool to analyze structural-acoustic problems. The most commonly used numerical prediction techniques for structural-acoustic problems are the deterministic element based methods, such as finite element method (FEM) and boundary element method (BEM). These element based methods use locally supported simple polynomials as shape functions within the elements. Given that these methods have no restrictions regarding the geometric complexity of a problem, they are efficient for analyzing a generally shaped model. However, the apparent drawback of these element based methods is the increase in number of elements and computational efforts to maintain reasonable prediction accuracy within high-frequency ranges and at short wavelengths. In addition, prediction results within the high-frequency range are substantially affected by interpolation and pollution errors. Thus, the practical applicability of element based methods is limited only to the low-frequency range. Statistical energy analysis (SEA) has many advantages for predicting system response within the high-frequency range. However, SEA application is limited only to the high-frequency range and is not valid for mid-low frequency range dynamic-response problems because of the modal density insufficiency of SEA for obtaining reliable results. A so-called mid-frequency gap exists between the application range of low-frequency and high-frequencies. This gap has no available mature and adequate prediction techniques, thereby leading to a very high computational loading for element-based methods and to a lack of randomness to make SEA applicable.
A novel and indirect Trefftz function-based deterministic prediction technique has been introduced to improve mid-frequency range computational efficiency and computational accuracy. The Trefftz method is a meshless numerical method for solving boundary value problems where approximate solutions are expressed as a linear combination of functions that automatically satisfy governing equations [1, 2]. The wave-based method (WBM) that is derived from the indirect Trefftz approach presents many advantages, such as relatively small system matrices, absence of pollution errors, and capacity to relax the frequency limitation [3]. WBM is suitable for coping with the mid-frequency dynamic problem through an enhanced computational efficiency. WBM divides the problem domain into a limited number of large sub-domains instead of dividing the problem domain into a large number of elemental domains. In addition, WBM facilitates description of the dynamic-response variables by a set of wave function i.e., the exact solutions of the governing differential equations. This property of WBM implies that only an approximation is involved in the boundary conditions. Consequently, the system matrices are substantially smaller compared with the element-based methods. Furthermore, WBM degrees of freedom (DOFs) are the contributory factors of the wave functions in the field variable expansion that leads to a substantial reduction in DOFs. The resulting smaller system matrices result in a higher computational efficiency that makes WBM capable of predicting the dynamic-response problem in both low-frequency range and mid-frequency range.
Over the past 16 years, many WBM-results studies have dealt with several dynamic problems, such as plate-structural dynamic problems and interior/exterior acoustic-radiation problems [4, 5]. The basic principles of WBM for convex-plate problems have been discussed, and the beneficial convergence rate of WBM compared with that of either FEM or BEM has been validated for various two-dimensional (2-D) problem examples [6, 7]. WBM for the steady-state dynamic-response problem of thin, flat plates coupled at an arbitrary angle, including both out-of-plane and in-plane plate dynamic behaviors, has been discussed [8]. The purpose of the hybrid deterministic-statistical approach, in which both WBM and SEA are applied to deal with the mid-frequency problem, has been presented [9, 10]. WBM has also been applied to analyze the acoustic-radiation problem that involves uncoupled interior and exterior acoustic radiation in the acoustic cavity [11, 12]. Furthermore, many studies aimed at extending the application of WBM have been published. The structure-design sensitivity formulation of a semi-coupled structural-acoustic problem using the WBM has been implemented [13]. Moreover, the thin-plate vibration power flow problem with Kirchhoff plate bending theory has been analyzed with WBM theory, and results show that WBM is theoretically accurate [14].
However, one of the apparent disadvantages of WBM method is that, a sufficient condition for the WBM approximations to converge towards the exact solution is convexity domain of the considered problem. The tendency of the structural-acoustic domain to be non-convex is one of the general structural-acoustic problems. Thus, the main drawback of the WBM is its inability to deal with geometrically complex constructions. To maximize the computational efficiency of WBM, its application was limited to moderate geometrical complexity system [15]. Non-convex problems are partitioned into many convex sub-domains. However, increased numbers of sub-domains results in increased numbers of interfaces, it is a multi-domain problem. This relationship shows an example of a multi-domain problem, which leads to an additional computational loading during the course of WBM use. Moreover, some geometrical shapes such as plate with circular hole or inclusions cannot be divided into convex sub-domains. To alleviate this convexity-condition problem, two WBM extension tactics, including hybrid WBM-FEM and multi-level WBM, have been recently proposed. The hybrid WBM-FEM involves a combination of the geometrical flexibility of the structural FEM and the indispensable convergence properties of the WBM; computational efficiency is also assured [16, 17]. Consequently, to overcome the geometrical restrictions, B-spline function is used to describe the curved edges, and the numerical integration procedure is used to evaluate the weighted residual formulation of WBM, respectively [18]. In response to the unbounded problem, a significantly enhanced WBM multi-level conception version has been introduced to efficiently analyze 2-D acoustic scattering and inclusions problem [19, 20]. The basic theory of multi-level conception is to decompose the multiple scattering problems into a set of linked single-scattering problem; the multi-level theory has extended the application of WBM in the dynamic-response problem of plate structure with holes or inclusions [21]. The bounded Helmholtz problem with multiple inclusions has been demonstrated using an efficient and flexible numerical strategy called multi-level wave-based numerical modeling [22].
The present study aims to develop a new novel approach to utilizing WBM toward a concave domain structure by introducing multi-level theory and complement-graph conception. Theory of complement-graph conception is investigated to alleviate or remove some of the geometrical constraints upon WBM application. The rest of this paper is organized as follows. The basic formulation of WBM is reviewed in Section 2. The complement-graph conception is performed in Section 3. The validity and numerical efficiency of the proposed method, as well as concave-domain numerical implementation, are illustrated in Section 4. Finally, the conclusions are drawn in Section 5.
2. Basic formulation of WBM
According to the indirect Trefftz principle, the wave functions accurately satisfy the governing dynamic equations. The general WBM modeling procedure consists of four steps: 1) partitioning of the problem domain into a number of convex sub-domains, 2) wave function set selection of each convex sub-domain, 3) WBM system matrix construction by using a weighted residual formulation of the boundary and interface conditions, 4) solution formulation of the system of equations to generate the wave function contribution factors and post processing of the dynamic-response variables.
2.1. Problem description
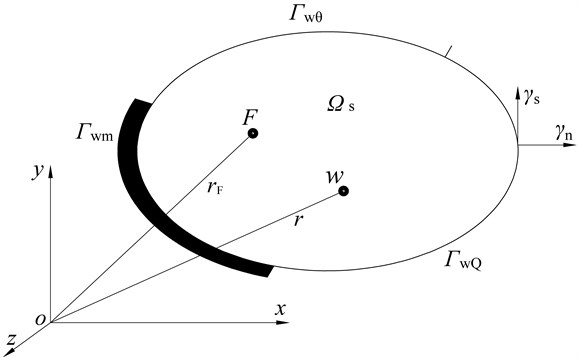
Basic principles of WBM for a general convex plate design domain are briefly discussed. As shown in the Cartesian coordinate system in Fig. 1, a thin-plate structure exists and is excited by a harmonic normal point force at position . In Fig. 1, is the structure design domain, and , and are the structure boundary conditions.
Fig. 1Convex plate domain
Two types of plate-bending theories exist, namely, Kirchhoff plate-bending theory and Reissner-Mindlin plate-bending theory. WBM as described in this research is based on the Kirchhoff plate-bending theory. In Kirchhoff theory, the rotational inertia and shear deformation effects are negligible. Considering the thin-plate structure problem, the Kirchhoff plate-bending theory could yields accurate results in low and mid frequency range. According to the Kirchhoff plate-bending theory, the time harmonic out-of-plane displacements function in the problem domain is governed by the following fourth-order partial differential equation:
where . is the 2-D Dirac-delta function. The bending wave number and the plate structure bending stiffness are defined as: and , respectively. In Eq. (1), symbols , , , , , and represent the plate thickness, material elasticity modulus, material Poisson’s ratio, circular frequency of bending wave, material loss factor, and plate material density, respectively. In addition, symbols is the unit imaginary number. Kirchhoff bending theory is tested to be correct when the bending wave length is six times greater the plate thickness .
In plate-structure dynamic-response analysis, Kirchhoff plate-bending theory is governed by a fourth-order equation differential equation that uniquely defines the displacement function . The boundary conditions are specified for each evaluated point in the plate-structure boundary. In addition, the boundary conditions of the considered plate domain has three parts (Fig. 1): 1) the kinematic boundary condition where the out-of-plane translational and the normal rotational displacements are imposed, 2) the mixed boundary conditions that impose the out-of-plane translational displacements and the normal bending moments, and 3) the mechanical boundary conditions that impose the normal bending moments and the equivalent shear forces.
The differential operators for the out-of-plate displacement, then the rotational displacement, bending moment and generalized shear force are defined as:
where and are the two arc coordinates in the normal and tangential directions of the plate-structure boundary, respectively.
2.2. The field variable expansion
For WBM application to bounded problems, the convexity of the considered problem domain is a sufficient condition for the theoretical convergence of WBM. This application approximated the field variables as an expansion based from functions that exactly satisfy the governing dynamic equations. In addition, an approximation error is induced in the boundary and interface conditions. Integrally minimizing this approximation error leads to the solution of the system.
In the considered design domain, the time harmonic out-of-plane displacement function is approximated by the following field variable expansion:
where each wave function satisfies the homogeneous part of the dynamic function shown by:
where and represent the unknown participation factors of wave functions; , and represent the and component of the wave vector, respectively; and is the number of wave functions. Function is a particular solution function to consider the inhomogeneous portion of the dynamic equation that arises from the external loading applied to the plate structure. In addition, the wave functions are restricted to the interval [−1, 1] in the application region to ensure that the amplitudes of the wave functions are less than 1.
The particular solution function satisfies the inhomogeneous part of the dynamic Eq. (1) arising from the external loading. Only an excitation by normal point forces is considered in this study, and the particular solution function for a point force loading of an infinite plate is given as:
where , is the zeroth-order Hankel function of the second kind. In Eq. (5), , and are the Bessel functions of the first and second kind, respectively.
2.3. Weighted residual formulation
The field variable Eq. (3) fits exactly with the governing dynamic Eq. (1), irrespective of the unknown wave function contribution factors . These contribution factors are determined by minimizing the approximation errors of the boundary conditions and the continuity condition through the weighted residual formulation. The weighted residual formulation of the boundary conditions is defined as:
Substitution of the field variable expansion and the weighting function expansion into weighted residual formulation leads to a typical WBM system solution.
2.4. Wave function selection
In general, an infinite number of wave functions can satisfy the homogeneous differential dynamic Eq. (1). To apply WBM in numerical analysis, wave functions expansion must be truncated to a finite set. In WBM, the maximum wave number , i.e., , depends on the analysis frequency range and the dimensions of considered problem. Wave numbers ( or ) are selected based on the outline dimensions (×) of a (preferably the smallest) rectangular circumscribing the plate domain .
Among the first types of wave number, and are chosen such that an integer number of half wavelengths equals the length of the rectangular box in the corresponding direction. The other component of the wave number is calculated from the wave number of the considered frequency. Vanmaele [6] has proposed two sets of wave functions, shown in Eq. (7). The first set of wave functions is cosine function-related whereas the second set is sine function-related. The two types of wave function are written as:
Desmet [4] proved that the first group of wave functions is theoretically sufficient for the convergence of the WBM in the convex-considered domain. In this study, the cosine-associated wave functions are chosen, and wave numbers can be expressed as:
Among the plate structure domain, the number of bending wave functions that are included in the field variable expansion in Eq. (3), is related to the excited force frequency and the dimensions of the enclosing rectangular box: .
However, finite wave functions can only be used in practical calculations. An infinite number of wave functions should satisfy the homogeneous differential equations. Therefore, the set of wave functions is truncated by applying a frequency-dependent truncation rule. The truncation rule is stated as:
where (2) is the truncation coefficient; a truncation coefficient of 10 is adopted in this study. The integer truncation value and . and are the length parameter and width parameter of the smallest rectangle around the outline domain, respectively. Through this formula, the largest wave number of the bending wave functions included in the plate structure is obtained within the considered frequency. As a result, the number of wave functions increases approximately linearly with excitation frequency.
3. Multi-level modeling analysis
This section presents an efficient extension of multi-level modeling approach to the concave domain by using the complement-graph conception.
3.1. Basic conception of multi-level modeling
A sufficient condition to ensure the convergence of WBM is that the design domain should be convexity domain. This is the main drawback of WBM. In response, the non-convex problem geometries must be decomposed into many convexity sub-domains. As a result, when the number of sub-domains increases, the integration length also increases. This further leads to an additional computational loading. On the other hand, some geometrical shapes, such as problem domain with circular and elliptic shapes, cannot be divided into convex sub-domains. To deal with this problem, two kinds of approaches aim to overcome these limitations were introduced recently. The first method involves use of multi-level modeling framework to alleviate the problems considered domain decomposition and geometrical requirement of structural problems with inclusions. The second approach is utilizing a hybrid FE-WBM formulation, i.e., FEM is applied in complex domain, whereas WBM is applied in convex domain. The multi-level modeling approach is also presented in this paper.
The theoretical basis for the multi-level conception is the superposition principle and the multiple-scattering theories. In the multi-level theory of WBM, the original problem can be decomposed into a single bounded sub-problem and one or more unbounded sub-problems (also termed levels). The bounded sub-problem boundary matched the boundary of original problem. In addition, the unbounded sub-problems boundary matches as well as the original problem boundary. Subsequently, the original problem is decomposed into the following levels with corresponding wave function sets, boundary residuals, and weighting functions. In the multi-level theory, the dynamic-response of various levels is superposed to form the dynamic response of the original problem.
Considering that the original problem converted bounded levels to unbounded levels, the former contains no holes or inclusions, and WBM tools become usable. In the multilevel modeling, the bounded levels describe the interior dynamic behavior of bounded sub-problems. Meanwhile, the unbounded levels consider the scattering behavior of an inclusion in an infinite homogeneous medium to model one hole or inclusion in an infinite domain. Consequently, this technique facilitates obtaining efficient and flexible numerical tactics for analyzing the mid-frequency dynamics of complex geometrical domain.
To model these unbounded parts, new wave function sets are defined for unbounded plate problems. The solution function is written as the superposition of several field variable expansions and , which need to satisfy the governing equation. The wave function of bounded fields should fit the non-reflecting boundary conditions imposed at . Meanwhile, the wave function of unbounded fields should satisfy the non-reflecting boundary conditions imposed at . Modeling each of the sub-problems using WBM and coupling them using the superposition principle help obtain the consequent response fields of the original problem.
A multilevel modeling approach is developed for unbounded acoustic multiple-scattering problems. The procedure for this approach involves four steps: 1) division of the original problem into various levels containing unbounded and bounded sub-domains; 2) selection of wave functions for each level containing a sub-domain design i.e., a wave function that can represent any arbitrary field on that boundary; 3) construction of the system of equations, and the weighted residual formulation; and 4) solution formulation and post-processing showing each point representing combined levels. Through this modeling technique, the dynamic-response problem of domain with concave boundary is investigated.
3.2. Basic conception of complement graph
The discussion on multi-level modeling in the previous section illustrates the feasibility and efficiency to cope with the 2-D domain problem through multiple circular holes or square holes [19]. However, some difficulties are encountered, such as the concave-domain problem.
To overcome these geometrical limitations in WBM, a complement-graph conception is proposed in this study. The multi-level modeling theory and superposition principle constitute the basic foundation of complement graph-conception. As shown in Fig. 2(a), a concave domain consists of two kinds of boundary characteristics i.e., convex curve , and concave curve . Considering the curve , the concave domain could not be divided into many kinds of convex sub-domains, and the traditional multi-level modeling could also not solve this problem. To deal with these concave-domain problem limitation, the addition a convex complement graph domain on to the concave boundary curve , as shown in Fig. 2(b), results in a new convex domain . In this study, the added convex-domain is named the complement graph.
As shown in the Fig. 2, the concave domain has two convex boundaries, . The concave domain also has two convex boundaries, . Defining the convex domains of and as levels renders multi-level modeling theory applicable. Apparently, the convex design domains and , are easy to deal with through WBM theory. In the next section, the feasibility and efficiency of complement-graph conception is illustrated through numerical verification studies where methodology is applied for Kirchhoff plate-bending problems.
Fig. 2Complement-graph conception
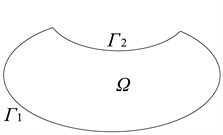
a)
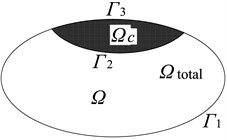
b)
3.3. An application of complement graph
The concave-domain problem is discussed in this section. Combination complement-graph conception and multi-level modeling theory are considered, and the application of the problem is shown in Fig. 3.
Fig. 3Complement graph method
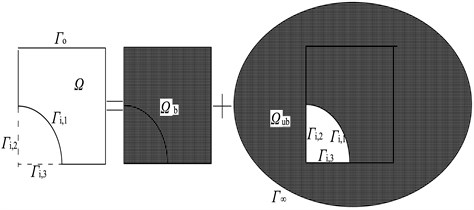
According to traditional WBM and multi-level modeling, accurately modeling this plate structure accurately (Fig. 3) is possible. Dividing the concave problem into convex sub-domains is also impossible. The quarter circle boundary could be approximated by a large number of straight edges, but this step leads to a rough approximation and a large number of sub-domains. Consequently, the computational efficiency of WBM is jeopardized
Through the multi-level approach and complement-graph conception, the concave domain problem is decomposed into two levels: one bounded level and one unbounded level that are both coupled at the boundaries. The bounded levels describe the interior dynamic response behavior of the bounded sub-problems with boundaries . The unbounded levels consider the scattering behavior of an inclusion in an infinite homogeneous medium, with inner boundaries . The solution field function is written as the superposition of several fields, and , which is required to satisfy the governing Kirchhoff plate-bending equation. Furthermore, the unbounded fields should also satisfy non-reflecting boundary conditions imposed at .
3.4. Wave functions of complement graph
After identifying the field variable expansions for the different levels, they combined with the common domain by using the superposition principle. In the bounded domain , the bounded wave functions should be defined based on the indirect Trefftz principle that is shown by Eq. (4).
In a similar manner, the unbounded wave functions should be defined based on the indirect Trefftz principle; the wave function can be written as: , where no external force is applied within the considered unbounded level.
To satisfy the Kirchhoff plate-bending theory, a sufficient condition is achieved when unbounded wave functions satisfy either or and the non-reflecting boundary conditions imposed at boundary . Considering the purely outgoing nature of the sub-domain, extra caution is unnecessary. Furthermore, the sub-domian is implicitly represented in the wave function set [22].
After defining the wave function of the unbounded domain and bounded domain, the field variable expansions of bounded and unbounded levels are combined using the superposition principle. Consequently, the multi-level field variable expansion can be stated as:
where is the solution of the bounded domain problem, and is the solution of the unbounded domain problem. Consequently, the composite multi-level function set is defined, and the wave model can be constructed by enforcing the boundary conditions through the application of a weighted residual formulation. This formulation is analogous to the weighted residual formulation for bounded problems Eq. (6) introduced in Section 2, but residuals are now expressed in terms of the new, composite wave function set. Using the weighted residual formulation, the proposed multi-level displacement expansion and weighting function expansion leads to a linear system of algebraic equations. These equations could be solved to obtain the wave function contribution factors of the displacement of the considered problem domain .
4. Numerical results and discussions
To demonstrate the efficiency and feasibility of the non-convex domain complement-graph conception and multi-level modeling, a plate structure under the external harmonic excitation in the air is presented. The convergence of the WBM is verified, and WBM predictions are compared with those obtained with the FEM.
4.1. Model description
Taking for example a rectangle plate with one elliptic cut-out in the left-bottom corner, the calculation of the vibration by the WBM is carried out. Fig. 4 shows the geometry of the considered problem.
Fig. 4Rectangle plate
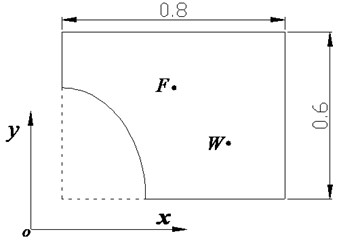
A rectangle plate containing one elliptic cut-out in the left-bottom corner is excited by a harmonic mechanical loading with prescribed under excitation frequency, amplitude, and direction. The boundary of the plate is simply supported. The semi-major axis and semi-minor axes of the ellipse are 0.4 m and 0.3 m, respectively. A unit point time-harmonic force with direction is applied at point (m, m), as shown in Fig. 4. Two evaluation points location point locations exist, i.e., (m, m) and (0.6 m, m).
For rectangle plate structure, the rectangular Cartesian coordinate system is used, with the coordinate origin set at the ellipse center. The length of plate is 0.8 m, the width is 0.6 m, and thickness is 0.001 m. The plate is steel based, and the mechanical properties of this steel are shown in Table 1.
Table 1Mechanical properties of materials
Material | Elasticity modulus (MPa) | Poisson ration | Loss factor | Density (kg·m-3) |
Steel | 210 000 | 0.3 | 0 | 7800 |
4.2. Calculation and comparison
Fig. 4 shows the impossibility to divide the problem into convex sub-domains, and traditional WBM could not to deal with this problem. Through the complement-graph conception and the multi-level modeling theory, the multi-level WBM is introduced. In the numerical calculation, the variations of vibrations are with the frequency ranges 0-800 Hz, and the frequency step size is 2 Hz. to compare the computational efficiency of multi-level WBM and FEM in the low and mid frequency range, convergence analysis of structural dynamic response is performed.
In the dynamic-response analysis, the truncation coefficient is defined as 10 to illustrate that the multi-level extension of WBM accurately describes the dynamic response behavior. In addition, multi-level WB model contains only 250 basis functions in the displacement expansion (150 bounded and 100 unbounded wave functions). Furthermore, WBM is implemented in the MATLAB/R2007 environment.
Considering that the business software MSC.Patran/Nastran is a proven and widely used numerical tool for structural dynamic-response analysis, all FEM predictions are calculated using MSC/Nastran 2005. The finest 8-noded Nastran model is defined as a reference for convergence curves. To ensure high numerical precision, the model is fine meshed and consisted of 78 200 quadratic elements within the plate structure.
Fig. 5 shows a contour of the structural displacement at 500 Hz obtained using both MSC/Nastran 2005 and a multi-level WBM. Results show that multi-level WBM can accurately describe the spatial distribution of the dynamic displacement field by using complement-graph conception. Fig. 5 shows that using WBM can achieve accuracy similar to FEM but with less DOFs and fast convergence. In the other frequencies, the displacement contour plots are considerable correlate.
Fig. 5Comparison of predictions in the displacement response of WBM and FEM
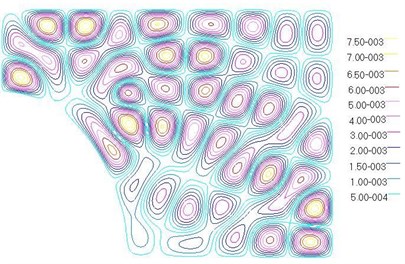
a) WBM, 250 DOFs
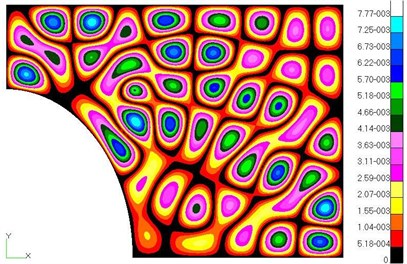
b) FEM, 196167 DOFs
Fig. 6 compares the predicted displacement response for evaluation point W within (0-800 Hz) frequency and the technique includes both FEM and multi-level WBM. Fig. 7 compares the predicted displacement response for evaluation point within (0-800 Hz) frequency and the technique also includes both FEM and multi-level WBM.
According to Figs. 6 and 7, multi-level WBM predictions considerable agree with conventional prediction techniques such as FEM throughout the entire frequency range of interest. Compared with FEM, WBM has less computational loading and more efficient convergence properties.
Fig. 6Displacement response at point W
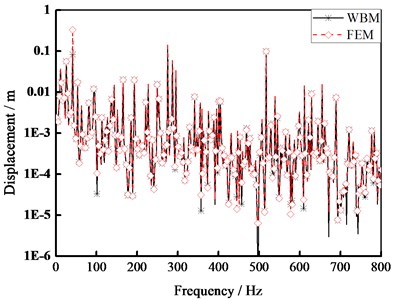
Fig. 7Displacement response at point F
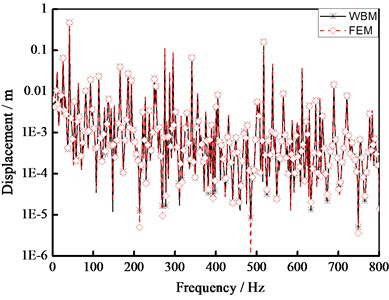
Comparison of data in Figs. 5-7 reveals that the numerical result of Patran/Nastran and WBM are similar, whereas WBM has less DOFs than that using MSC/Nastran soft code. Generally, these examples show that the multi-level WBM for plate-bending problems perform better than FEM within both low and mid frequency ranges.
Numerical results exhibit considerable improvement in terms of efficiency in concave problem by using the complement-graph conception and multi-level modeling theory. Numerical results show that the multi-level multi-level modeling theory of WBM can accurately describe the spatial distribution of the dynamic displacement field combination through complement-graph conception. Similar, displacement contour plots are considerably correlated within different frequency ranges.
4.3. Convergence analysis
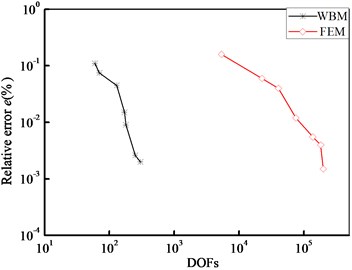
The accuracy of FEM analysis depends on the number of elements, selected shape functions. While, the accuracy of WBM analysis depends on the number of wave function. Fig. 8 plots the variation in relative errors and the degrees of freedom (DOFs) for the displacement prediction amplitudes of point (m, m) at 500 Hz frequency.
Fig. 8 shows that WBM has better convergence than element based methods. The high computational efficiency is likely to become even more definite.
Fig. 8Comparison of the convergence of FEM and WBM
5. Conclusions
WBM is applied to plate-bending vibration, with special focus on the concave-domain problem. A new approach is also introduced for the non-convex domain problem. Complement-graph conception effectiveness for concave-domain problem is investigated through a plate structure as a numerical example. The potential of enhanced WBM is demonstrated through validation examples. The application of more complex concave problem such as three-dimensional vibro-acoustic concave-domain problem requires further studies.
References
-
Chen J. T., Wu C. S., Lee Y. T., et al. On the equivalence of the Trefftz method and method of fundamental solutions for Laplace and biharmonic equations. Computer Methods in Applied Mechanics and Engineering, Vol. 53, 2007, p. 851-879.
-
Kovalevsky L., Riou H., Ladevèze P. A Trefftz approach for medium-frequency vibrations of orthotropic structures. Computers and Structures, Vol. 143, 2014, p. 85-90.
-
Wen P. H., Aliabadi M. H. Analysis of functionally graded plates by meshless method: a purely analytical formulation. Engineering Analysis with Boundary Elements, Vol. 36, 2012, p. 639-650.
-
Desmet W. A Wave Based Prediction Technique for Coupled Vibro-Acoustic Analysis. Ph.D. Dissertation, Katholieke Universiteit Leuven, 1998.
-
Deckers E., Atak O., Coox L., et al. The wave based method: an overview of 15 years of research. Wave Motion, Vol. 51, 2014, p. 550-565.
-
Vanmaele C., Vandepitte D., Desmet W. An efficient wave based prediction technique for plate bending vibrations. Computer Methods in Applied Mechanics and Engineering, Vol. 196, 2007, p. 3178-3189.
-
Chen M. X., Wei J. H., Xie K., et al. Wave based method for free vibration analysis of ring stiffened cylindrical shell with intermediate large frame ribs. Shock and Vibration, Vol. 20, 2013, p. 459-479.
-
Vergote K., Vanmaele C., Vandepitte D., et al. An efficient wave based approach for the time-harmonic vibration analysis of 3D plate assemblies. Journal of Sound and Vibration, Vol. 332, 2013, p. 1930-1946.
-
Vergote K., Genechten B. V., Vandepitte D., et al. On the analysis of vibro-acoustic systems in the mid-frequency range using a hybrid deterministic-statistical approach. Computers and Structures, Vol. 89, 2011, p. 868-877.
-
Vergote K., Vandepitte D., Desmet W. On the use of a hybrid wave based-statistical energy approach for the analysis of vibro-acoustic systems in the mid-frequency range. Proceeding of ISMA2010, 2010, p. 2437-2450.
-
Pluymers B., Vandepitte D., Desmet W. Application of an efficient wave based prediction technique for the analysis of vibro-acoustic radiation problems. Journal of Computational and Applied Mathematics, Vol. 168, 2004, p. 353-364.
-
Deckers E., Vandepitte D., Desmet W. A wave based method for the axisymmetric dynamic analysis of acoustic and poroelastic problems. Computer Methods in Applied Mechanics and Engineering, Vol. 257, 2013, p. 1-16.
-
Koo K., Pluymers B., Desmet W., et al. Vibro-acoustic design sensitivity analysis using the wave-based method. Journal of Sound and Vibration, Vol. 330, 2011, p. 4340-4351.
-
Vergote K., Vandepitte D., Desmet W. Application of the wave based method for the calculation of structural intensity and power flow in plates. Proceeding of ISMA2008, 2008, p. 1653-1666.
-
Genechten B. V., Bergen B., Pluymers B., et al. A novel modelling approach for sound propagation analysis in a multiple scatterer environment. The Journal of the Acoustical Society of America, Vol. 123, 2008, p. 5223-5228.
-
Hal B. V., Desmet W., Vandepitte D. Hybrid finite element-wave based method for time harmonic interior structural-acoustic problems. Computers and Structures, Vol. 83, 2005, p. 167-180.
-
Genechten B. V., Vandepitte D., Desmet W. A direct hybrid finite element-wave based modelling technique for efficient coupled vibro-acoustic analysis. Computer Methods in Applied Mechanics and Engineering, Vol. 200, 2011, p. 742-764.
-
Deckers E., Drofmans B., Genechten B. V., et al. Spline-based boundaries: a first step towards generic geometric domain descriptions for efficient mid-frequency acoustic analysis using the wave based method. Journal of Computational and Applied Mathematics, Vol. 235, 2011, p. 2679-2693.
-
Riou H., Ladevèze P., Kovalevsky L. The variational theory of complex rays: an answer to the resolution of mid-frequency 3D engineering problems. Journal of Sound and Vibration, Vol. 332, 2013, p. 1947-1960.
-
Genechten B. V., Bergen B., Vandepitte D., et al. A Trefftz-based numerical modelling framework for Helmholtz problems with complex multiple-scatterer configurations. Journal of Computational Physics, Vol. 229, 2010, p. 6623-6643.
-
Vergote K. Dynamic analysis of structural components in the mid frequency range using the wave based method. Ph.D. Dissertation, Katholieke Universiteit Leuven, 2012.
-
Genechten B. V., Vergote K., Vandepitte D., et al. A multi-level wave based numerical modelling framework for the steady-state dynamic analysis of bounded Helmholtz problems with multiple inclusions. Computer Methods in Applied Mechanics and Engineering, Vol. 199, 2010, p. 1881-1905.
About this article
This work was partially supported by the Youth Fund of State Key Laboratory of Ocean Engineering (Grant No. GKZD010059-22) of Shanghai Jiaotong University. This support is gratefully acknowledged by the authors.
