Abstract
The disadvantages of linear arrays are such that the range of damage detection is limited up to only 180°, and also that the detection accuracy is very poor at angles close to 0° and 180°. In order to solve this problem, this paper puts forward a new damage detection and localization method by coupling the image enhancement technology with two-dimensional piezoelectric ultrasonic phased arrays arranged in the shape of a cross. The basic detection principle as well as the detailed process of damage localization will be covered in this paper. Along with the implementation of the cross-shaped sensor arrays, a new image enhancement algorithm is proposed with the aim to deal with the problem of phantom image emerging in the opposite side of the original image. The results of the experiments conducted on an aluminum plate show that the above proposed method can not only effectively solve the limitation of the linear sensor array, but also accurately detect multiple damages in full angle mode.
1. Introduction
Structural health monitoring (SHM) of plate-like structures has become a popular topic of research [1-3]. Many methods of structural damage detection have been focused on the application of Lamb waves, including the time reversal imaging technology [4-6], the spatial filter method [7, 8] and the ultrasonic phased array method.
The performance of a SHM system can be enhanced by the means of active ultrasonic phased arrays due to their superior signal-to-noise ratio and beam-steering capability [9, 10]. The linear ultrasonic phased array, being one of the simplest and most widely used arrays, have been well explored and developed [10, 11]. However, the linear array-based ultrasonic phased array was found to possess several fundamental disadvantages, as follows. Firstly, it does not cover the whole azimuth angular system (0°-360°) and it has very poor accuracy at the angles close to 0° and 180°. Secondly, linear arrays suffer from front-back ambiguity (mirror effect), which makes it impossible to distinguish targets located in front and behind of the array.
The above problems can be diminished by the use of 2-D arrays. Different 2-D array configurations were also researched in several papers. Giurgiutiu et al. [10] studied the two-dimensional array beam direction, and carried out crack detection experiment using a rectangular array. Wilcox [12] proposed a circular ultrasonic phased array and conducted a damage detection experiment based on it. Malinowski [13] put forward a star-shaped array, and verified its crack detection efficiency on an aluminum plate.
The cross-shaped array is a relatively simple 2-D array, not only in terms of its configuration, but also in terms of its imaging algorithm complexity. However, as predicted by Yu’s beamforming analysis [14], in the directions along the array’s alignments, duplicated beams emerged in the opposite side of the original beams (180°for beamforming at 0°, and 270° for beamforming at 90°). To overcome this limitation and to realize 360° full angle detection, an image enhancement algorithm, suitable for both single and multiple damage detecton, is also investigated in this paper. Through experiments on an aluminum plate, the Lamb wave signal is analyzed in detail, the full-angle multiple-damage monitoring with high measurement accuracy on an aluminum plate is realized.
2. Cross-shaped ultrasonic phased array
2.1. Cross-shaped array signal model
The layout of the cross-shaped array is as illustrated in Fig. 1. Two linear piezoelectric transducer (PZT) arrays labeled No. 1 and No. 2, consist of and PZT elements with inter-element spacing of and respectively, are aligned along the and axes, with the mid-point of each array meeting at the axes’ origin. For a distant point , refers to the vector spanning from the origin topoint . Because , (), the rays connecting point and each of the respective sensors can be assumed to be parallel with each other, inclined at angle .
Fig. 1Cross-shaped array
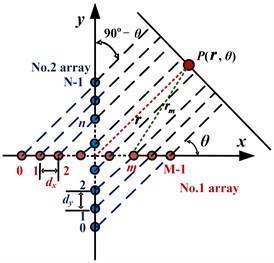
It is assumed that each PZT element of the cross-shaped array is excited and Lamb waves generated on the plate will reach point . The synthetic signal can be broken down into signal components that excited all the piezoelectric patches of No. 1 and No. 2 arrays, denoted by and respectively.
For the far field case, , . If the weights are chosen as unity, 1, and thus the synthetic wave front that reaches , propagating from the total of PZT elements of the No. 1 array can be represented by:
where is wave frequency, is the Lamb wave velocity on the structure.
To steer the output wave front into a certain direction, the delays are introduced. Eq. (1) becomes:
Similarly for , the delays are introduced:
If the time delay is chosen as shown by Eqs. (4) and (5), the maximum of the beam forming factor can be achieved, and the synthetic signal will be strengthened by times with respect to the individual reference signal . Likewise, the synthetic signal will then be times the individual reference signal . The resulting forms of the synthetic signals are presented as in Eqs. (6) and (7):
Hence, the overall synthetic signal of cross-shaped array can be expressed as:
Based on the principle of reciprocity, the receiving process must be consistent with the exciting process, given that the same conditions apply within the two processes. Therefore, according to the stated principle, let’s say that the excited signals left the PZT elements within a set of specific time delays, the returning signals should be able to arrive at all the PZT elements at the same time:
2.2. Damage localization
When the signal beam points at the direction towards the damage location, all signals will be focused, and the energy of combined signal will be enhanced. Subsequently, the signal energy reflected by damage is also the strongest in this direction. Information related to the damage angle can thus be obtained according to this principle. By analyzing the signal in the damage direction, the damage distance r can be calculated as:
where is the time of arrival of the signal in the damage direction.
2.3. Image enhancement
The scan images can be obtained by displaying the energy of synthetic signal from all directions on the polar coordinate plane in a gray level resolution. The appearance of phantom images in the opposite side of cross-shaped array synthetic signal will affect the result of damage localization, especially for the case of multiple damages. An image enhancement method is proposed in order to make the damage scan image clearer. The synthetic signals is firstly normalized, and then the exponential function algorithm is taken into account. The function is shown below:
where is the amplitude of the synthetic signals before optimization, is the corresponding synthetic signal amplitude after the optimization. is the power of exponential function, which is equivalent to the size of the control value of the original image used to enhance the contrast of the gray value of each part.
3. Experimental setup
3.1. The experimental system
It can be seen from Fig. 2(a) that the experimental setup consists of an aluminum plate, a cross-shaped PZT array and a multi-channel scanning systems developed by Nanjing University of Aeronautics and Astronautics laboratory [15]. The dimension of the aluminum plate is 1000 mm×1000 mm×2 mm, whereas the diameter and thickness of each of the PZT elements are 8 mm and 0.48 mm respectively. Each of the linear arrays of the cross-shaped PZT array is made up of seven PZT elements with a 9 mm spacing between two adjacent elements. The PZT elements for both linear arrays are labeled as PZT0 to PZT6. PZT3, being the mutual element, and also the center point of both linear arrays in this case, is set as the coordinate’s origin. A 2 kg weight with a diameter of 20 mm is used to simulate the damage.
Fig. 2Experiment setup and the damages position (unit: mm)
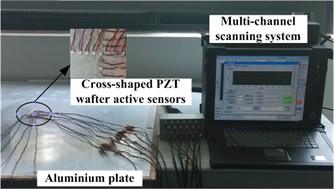
a) Experimental setup
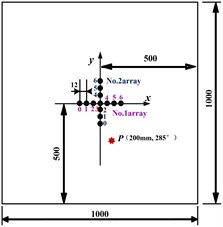
b) Single damage position
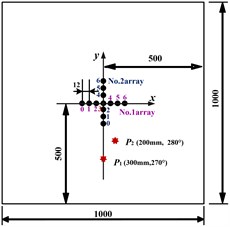
c) Multiple damages position
3.2. Single damage detection and localization
The excitation signal is the modulate five-cycle sine burst, while the excitation frequency is set at 40 kHz where mode sensor signal amplitude dominates that of the mode, which is believed to be conducive to the signals’ analysis. The sampling frequency is set at 2 MHz, and 1300 points are collected.
The positions of the damage and the PZT elements are as shown in Fig. 2(b). Actual damage point (200 mm, 285°) is adopted. Data collection is conducted in a round-robin pattern. In each turn, one element plays the role of a transmitter and sends out excitation while the rest serve as receivers and pick up the reflections of both arrays. All the elements in the array take turns to serve as transmitters. The received signals in the health status and the damage status are called the health and damage signals respectively. The differential signals between the health and damage signals are called damage reflection signals, which are delayed and superimposed according to the beam angle delay formula to obtain the synthetic damage reflection signal.
It can be found that when the maximum synthetic signal is directed at the actual damage angle of 285°, a mirrored synthetic signal shows up symmetrically at 75°, as shown in Fig. 3(a). It is proved that when there is only one working linear array, in this case, the No.1 array, a phantom image will also appear on the scan image. This phenomenon of inherent mirror symmetry subsequently results in the inspection area being limited to, at most, 180°.
Likewise, from what can be seen in Fig. 3(b), if only the No. 2 array is used to detect damage, problems will also occur. In this case, since the 285° damage angle is located very close to the array (or the -axis), not only that a phantom image is seen, but it also appears to be connected to the image of the actual damage, which makes it more difficult to identify the actual damage location. Then, the fusion of two linear arrays’ signal detection algorithm is adopted. It was found that the resulting scan image displays the superposition of the the two problematic linear arrays’ scan image, as can be seen in Fig. 3(c).
Fig. 3Damage detection figure
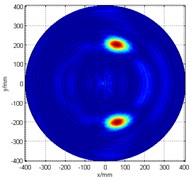
a) No. 1 array only
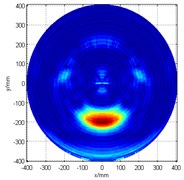
b) No. 2 array only
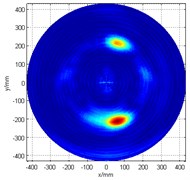
c)The original image
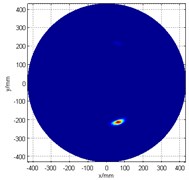
d) The image after enhancement
In order to reduce the effect of the unwanted phantom image as well as to improve the damage recognition quality, an image enhancement method is applied to optimize the image by setting the exponential power in Eq. (11) to 5. The enhanced damage scan image is shown in Fig. 3(d). The detection result is (210 mm, 287°), with an angular error of 2°, and positional error of less than 1 cm (actual damage location is (200 mm, 285°)). This result proved that the combination of the cross-shaped ultrasonic phased array and image enhancement method can effectively identify the structural damage.
3.3. Multiple-damage detection and localization
The combination of the cross-shaped ultrasonic phased array and the image enhancement method can also be used for multiple damages identification. Its principle and recognition process is similar to that of the singular damage identification. The damage positions and the layout of the piezoelectric elements are shown in Fig. 2(c). The actual damage points are (300 mm, 270°) and (200 mm, 280°).
Fig. 4Multiple-damage detection figure
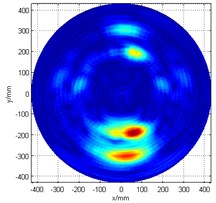
a) The original image of cross-shaped array
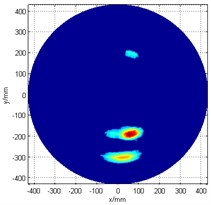
b) The image after enhancement
The pre-enhanced cross-shaped array damage scan image is as shown in Fig. 4(a). This time, a smaller power of exponential function was chosen to help ease the detection of damage , since its energy is not so strong. A threshold setting (60 % of the maximum value of the synthetic signal) was firstly applied, and then for the image enhancement processing, the exponential power is set to 2. Fig. 4(b) presents the post-enhancement damage detection scan image. The damage detection results are (210 mm, 273°) and (195 mm, 284°), which means that the angular error is less 4°, and the positional error is less than 2 cm when compared to the actual damage (300 mm, 270°) and (200 mm, 280°).
4. Conclusions
This paper proposes a damage detection method on plate-like structures which combines the use of cross-shaped piezoelectric ultrasonic phased array with an image enhancement algorithm. In order to verify the analysis and evaluate the practical applicability of the proposed method, an experiment was setup such that it was comprised of a cross-shaped array placed on a large aluminum plate, on which it was tested to detect a series of single and multiple damages. Results showed that the cross-shaped ultrasonic phased array can realize 360° full angle damage detection with a directional error estimated to be less than 4°, and a maximum positional error of less than 2 cm.
References
-
Derriso M., Pratt D. M., Homan D. B. Integrated vehicle health management: the key to future aerospace systems. Proceedings of the Fourth International Workshop on Structural Health Monitoring, 2003, p. 3-11.
-
Christian S., Manfred N. Structural health monitoring, in-service experience, benefit and way ahea. Structural Health Monitoring, Vol. 9, Issue 3, 2010, p. 209-217.
-
Trathen P. N. Structural health monitoring for corrosion on military aircraft. Materials Forum, Vol. 33, 2009, p. 450-456.
-
Wang C. H., Rose J. T., Chang F. K. A synthetic time-reversal imaging method for structural health monitoring. Smart Materials and Structures, Vol. 13, Issue 2, 2004, p. 415-423.
-
Wang L., Yuan F. Damage identification in a composite plate using pre-stack reverse-time migration technique. Structural Health Monitoring, Vol. 4, Issue 3, 2005, p. 195-211.
-
Wang Q., Yuan S. Baseline-free imaging method based on new PZT sensor arrangements. Journal of intelligent Material Systems and Structures, Vol. 20, Issue 14, 2009, p. 1663-1673.
-
Purekar A. S., Pines D. J., Sundararaman S., Adams D. E. Directional piezoelectric phased array filters for detecting damage in isotropic plates. Smart Materials and Structures, Vol. 13, Issue 4, 2004, p. 838-850.
-
Wang Y., Yuan S., Qiu L. Improved wavelet-based spatial filter of damage imaging method on composite structures. Chinese Journal of Aeronautics, Vol. 24, Issue 5, 2011, p. 665-672.
-
Yuan S. Structural Health Monitoring. Beijing, National Defence Industry Press, 2007, (in Chinese).
-
Giurgiutiu V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors. Academic Press, 2007.
-
Sun Y., Yuan S., Cai J. Using phased array technology in structure health monitoring. Journal of Astronautics, Vol. 29, Issue 4, 2008, p. 1393-1396, (in Chinese).
-
Wilcox P. D. Omni-directional guided wave transducer arrays for the rapid inspection of large areas of plate structures. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency, Vol. 50, Issue 6, 2003, p. 699-709.
-
Malinowski P., Wandowski T., Trendafilova I., Ostachowicz W. A phased array-based method for damage detection and localization in thin plates. Structural Health Monitoring, Vol. 8, Issue 1, 2009, p. 5-15.
-
Yu L., Giurgiutiu V. Design, implementation, and comparison of guided wave phased arrays using embedded piezoelectric wafer active sensors for structural health monitoring. Smart Structures and Integrated Systems, Vol. 6173, 2006, p. 1-12.
-
Qiu L., Yuan S. On development of a multi-channel PZT array scanning system and its evaluating application on UAV wing box. Sensors and Actuators A, Physical, Vol. 151, Issue 2, 2009, p. 220-230.
About this article
This work is supported by the Chinese National Foundation of Natural Science (No. 51205189), the National Scientific Funding for Distinguished Young Scholars (No. 51225502), the High-Proiority Academic Program Development of the Higher Education Institute of Jiangsu Province and the Qing Lan Project.
