Abstract
When the story heights of adjacent buildings are unequal, the inter-floor pounding maybe happen during earthquake. Employing substructures in pounding area, the analytical model of adjacent structures with unequal story height is developed, and the equations of motion considering pounding are derived. Based on analytical model, the inter-floor pounding responses of adjacent buildings with unequal story height are investigated. The corresponding parametrical studies are conducted and influence rules are concluded. The results show that the influences of inter-floor pounding in adjacent buildings on main structures are smaller than those of floor pounding. But the damages on pounding area are quite large. Moreover, the period ratio of structures, the initial gap and the pounding location have remarkable influence on responses of inter-floor pounding.
1. Introduction
During earthquake, adjacent-buildings will vibrate asynchronously due to different dynamic characteristics. If the gap between adjacent buildings is small, the pounding between structures would happen. The pounding may severely damage adjacent buildings, or even result in collapse of buildings [2].
After the Mexico Earthquake [3, 4], the pounding mechanism of adjacent buildings aroused widespread concerns of researchers. The early researches [5] simplified the target individual building to a Single-Degree-of-Freedom system. They neglected the influence of dynamic characteristics in adjacent structure, and treated it as rigid body with spring-damper system in the pounding points. After that, Maison et al. [6] developed the pounding model of flexible adjacent buildings, in which each individual building is treated as a Multiple-Degree-of-Freedom elastic system respectively and the collision point is simulated as a contact element. Through the study of seismic pounding responses, they discovered that the pounding response of building increased as the structural high and the structural rigid increased. Jankowski studied the influence of structural nonlinearity to the pounding of adjacent buildings [7] and found out that the influence of structural nonlinearity cannot be ignored in the analysis. Zou et al. [8] revealed that pile-soil-structure interaction (PSSI) has significant influence on pounding of adjacent high-rise buildings with flexible pile foundation. Later, Tubaldi [9], Zhao et al. [10] and Zhai et al. [11] have also performed related researches on the pounding of adjacent buildings.
These researches are mostly based on the hypothesis that the story heights of adjacent buildings are equal, i.e., pounding would happen in position of floors. However, the story heights of adjacent buildings are not always equal due to the different functions of buildings. Consequently, when the earthquake happens, inter-floor pounding would occur between adjacent buildings with unequal story height, i.e., the floor slab of one building pounds the column (or wall) of the other one. Because these members are the primary elements to carry vertical load of structure, such pounding would probably result in the collapse of whole structure. Therefore, Karayannis et al. [12] realized that pounding of adjacent buildings of unequal floor height is more dangerous than that of equal floor height. But so far, there is little research focused on this field.
The purpose of this paper is to build the pounding analytical model of adjacent buildings with unequal story height by adding substructures in pounding area, and to derive its motive equations of pounding. Basis on this, the related parameters study is conducted.
2. Analytical model of pounding
Both FEM and analytical derivation are two kinds of methods generally used in pounding investigation [13, 14]. There are two advantages of analytical derivation: i) From the procedure of analytical derivation, the theoretical model can be deeply understood; ii) Since the derived results usually integrated into computer programming, the computer code can be easily edited to conducted parametric study. So the analytical derivation method is employed in this study.
For the pounding of adjacent buildings with unequal story height occurs in inter-floor position, the analytical model of pounding include structure model, pounding element model and pounding point model.
2.1. Pounding element model
Fig. 1 shows the Hertz-damp pounding element model [17], which is adopted in this paper. The pounding force formula is:
where, is the unit step function, is the stiffness of impact spring, is the initial gap between pounding individuals, is the displacement of , is the displacement of . The nonlinear damping coefficient can be expressed as:
where, is a damping constant. According to the conservation law of energy, it is expressed as:
where, is the recovery coefficient, for concrete it is 0.65.
Fig. 1Hertz-damp model
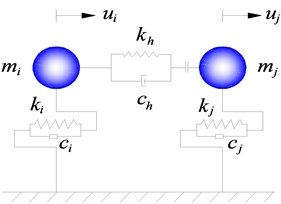
2.2. Pounding point model
For low-rise and moderate rise frame structures, the overall deflected shape under horizontal loading has a shear configuration with a maximum inclination near the base and a minimum inclination at the top. The dynamic responses of buildings can be simulated by dynamic responses of lumped-mass structure systems [15, 16]. In this study, the lumped story mass and story drift stiffness is hypnotized to represent general frame structures.
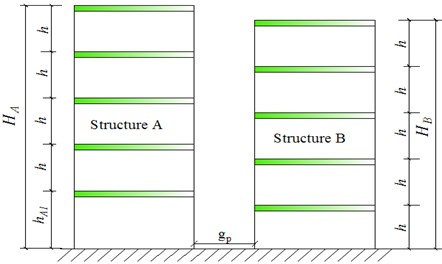
Fig. 2 shows an adjacent-building consisted of two individuals (structure A and B) with unequal story height. During earthquakes, the potential pounding would not occur between the floors of two individual buildings, but between the floor of one individual and the inter-floor position of another individual instead. Consequently, the stiffness and mass of the latter individual, which involved in the inter-floor pounding, is not the anti-pushing rigidity and mass of whole building, but those of local vertical members directly involved in the pounding.
Both of building A and B are simplified respectively to MDOF (multi-degree of freedom) shear type model, their mass, damping and stiffness of any floor are , , and , , respectively. Assuming they are frames of floors, spans and floors, spans respectively, and have multiple potential pounding points. Then, any individual building involved in inter-floor pounding can be considered that there is an additional substructure participated in pounding in the pounding area. Its mass is and respectively, whose value can be calculated according to the mass of actually involving in the pounding.
Fig. 2Calculation model of adjacent buildings with unequal floor height
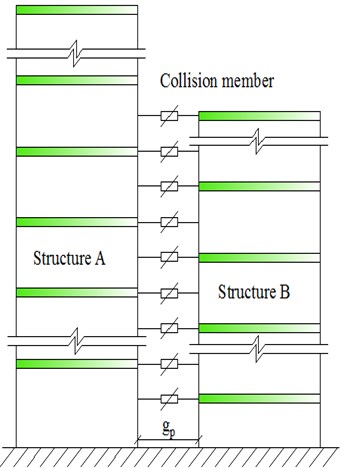
a) Schematic diagram of structure pounding
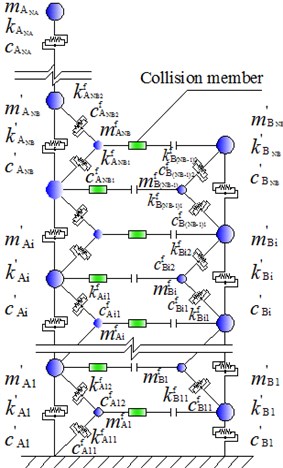
b) Calculating sketch of structure pounding
The stiffness of additional substructure can be determined by actual anti-pushing rigidities of vertical members involved in pounding. Taking building A for example, it is divided by pounding point into two parts ( and ), they can be calculated as followings:
where, , is the height of column under the pounding point, is the height of this floor. In the same way, the stiffness of substructure attached to structure B can be obtained by:
where, , is the height of column under the pounding point, is the height of this floor.
2.3. Pounding motion equation and solving
According to the analytical model above, the motion equation under earthquakes is obtained:
where, , and are mass, damping and stiffness matrix of structure (, ) respectively, , and are the acceleration, velocity and displacement vector of structure (, ) respectively, is the ground motion acceleration, and are unit vector, is the pounding force vector of structure (, ):
where, and are the mass matrix of primary structure A and B involved in pounding respectively (deduct corresponding mass of substructure), and are the mass matrix of additional substructure of A and B. They can be obtained by:
The matrices of stiffness are determined by the following formulas:
The detail block matrices are listed in appendix. Damping matrix is the linear combination of mass matrix and stiffness matrix. The Eq. (7) can be equivalently written as:
where:
The Eq. (11) can be solved by step-by-step integration method.
3. Numerical simulation
An adjacent-building consisted of two individuals with unequal floor height, structure A and structure B, is considered and shown in Fig. 2. Structure A is a reinforced concrete frame of 5 spans (4.5 m) and 5 stories, and its floor height of the first story and the others is 6 m and 4 m respectively. The mass of the first story, 2-4 stories and top story is 4.5×105 kg, 4.0×105 kg and 3.0×105 kg respectively. The stiffness of each story is 3.0×108 N/m; Structure B is also a reinforced concrete frame with 5 spans (4.5 m) and 5 stories (4 m), the mass of first story, 2-4 stories and top story is 4.5×105 kg, 4.0×105 kg and 3.0×105 kg respectively, and the stiffness of each story is 9.75×108 N/m. The parameters of member sections and additional substructures are shown in Table 1 and Table 2 respectively. The pounding stiffness is 8.68×104 kN/m3/2, the recovery coefficient is 0.65, and the structure damping ratio is 0.05. If there is no other special instruction, the site category is Category-2 (Chinese Code), the seismic fortification intensity is 8 degree (Chinese Code), and the initial gap is 0.01 m. The scaled ground motion of El-Centro earthquake (North-south component) with maximum acceleration of 400 Gal is used as the input excitation.
Table 1Member sections of structure A and structure B
Structure | Number of floors | Concrete grade | Section of column (mm2) | Section of beam (mm2) | Slab thickness (mm) | ||
Side | Inner | Side | Inner | ||||
A | 1 | C30 | 550×550 | 500×500 | 300×600 | 250×500 | 100 |
2-5 | C30 | 500×500 | 400×400 | 300×600 | 250×500 | 100 | |
B | 1 | C35 | 500×550 | 500×500 | 300×600 | 250×600 | 120 |
2-5 | C35 | 500×550 | 500×500 | 300×600 | 250×450 | 120 | |
Table 2Model parameters of adjacent structures
Parameter | Structure A (number of floors) | Structure B (number of floors) | |||||||||
1 | 2-4 | 5 | 1 | 2-3 | 5 | ||||||
Main mass (105 kg) | 4.3 | 3.8 | 2.9 | 4.4 | 3.8 | 2.9 | |||||
Stiffness (108 N/m) | 2.52 | 2.52 | 2.52 | 8.19 | 8.19 | 8.19 | |||||
Added mass (105 kg) | ~ | – | ~ | ||||||||
0.2 | 0.2 | 0.2 | – | 0.2 | 0.2 | ||||||
Added stiffness (108 N/m) | – | – | |||||||||
0.65 | 1.85 | 0.96 | – | 0.96 | 0.96 | – | 3.12 | 3.12 | 3.12 | 3.12 | |
3.1. Pounding response analysis
In order to study the influence of unequal floor height on pounding responses of adjacent buildings, supposing all other conditions remain equal, the responses of each building under three working cases, (1) no pounding, (2) pounding of equal floor height, (3) pounding of unequal floor height, are calculated shown in Figs. 3-8.
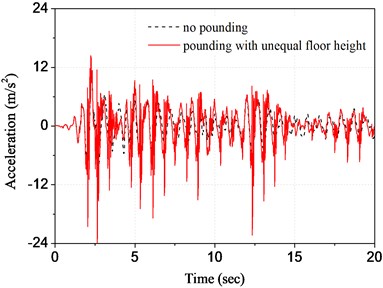
Fig. 3 and Fig. 4 show respectively the displacement and the acceleration time history in top floor of structure A under different working case. From the figures we can see, whether floor pounding for equal floor height structures or interfloor pounding for unequal floor height structures, their pounding acceleration responses are all much larger than that of no pounding. For example, the peak acceleration response of pounding for equal floor height structures is 18.981 m/s2, which is nearly three times as much as that of no pounding. Yet, the growth of displacement is not remarkable. It indicates a fact that pounding of adjacent buildings can generate large acceleration pulse, which is usually much larger than seismic pulse. However, as a result of mutual support between individual buildings, the displacement increase of pounding is not very big. On the contrary, this pounding displacement is even smaller than corresponding seismic displacement sometimes. Due to the stiffness of substructure is smaller than that of main structure, in contrast, the acceleration pulse of main structure generated by interfloor pounding is smaller than that generated by floor pounding.
Fig. 3Time history of top floor displacement of structure A
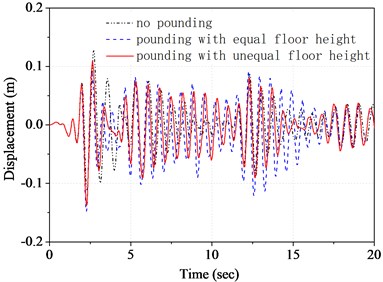
Fig. 4Time history of top floor acceleration of structure A
Fig. 5Time history of forth floor pounding force of structure A
Fig. 6Time history of top floor pounding force of structure B
From Fig. 5 and Fig. 6, which is time history of pounding force for the corresponding floor of structure A and structure B respectively, we can also see that the pulse of pounding force generated by floor pounding is much larger than that generated by interfloor pounding, approximately as 2 times as the latter. The main reason is, during interfloor pounding, the pounding participants are just local substructures. Their stiffness and mass are much smaller than those of main structure, and hence, the influence on main structure is also smaller.
However, it doesn’t mean that the interfloor pounding is safer than the floor pounding. Figs. 7 and 8 are the time histories of pounding response for substructure A under different working cases. It shows that the peak acceleration response of interfloor pounding for substructures runs up to 24.623 m/s2, which is even larger than main structure seismic response of corresponding floor with no pounding, and can result in damage to substructures readily. Moreover, the pounding participants, i.e. substructures, are generally main members of vertical baring force for main structures, and their failure can result in serious damage or even collapse to main structure.
Fig. 7Time history of top floor displacement of substructure A
Fig. 8Time history of top floor acceleration of substructure A
3.2. Influence of period ratio
In order to study the influence of dynamic characteristics of adjacent structures on interfloor pounding, a non-dimensional parameter of pounding displacement ratio is defined:
where, is the maximum displacement of structure after pounding, is the maximum displacement of structure with no pounding. Supposing other conditions are the same, the curve of and pounding force varied with ratio of period are obtained and shown in Fig. 9 and Fig. 10 respectively.
Fig. 9Displacement ratio of top floor varying with ratio of period
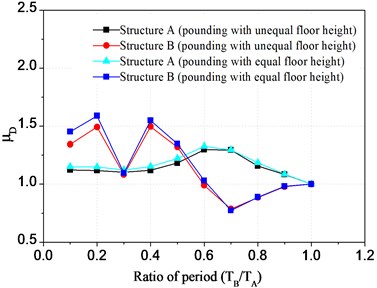
Fig. 10Pounding force of top floor varying with ratio of period
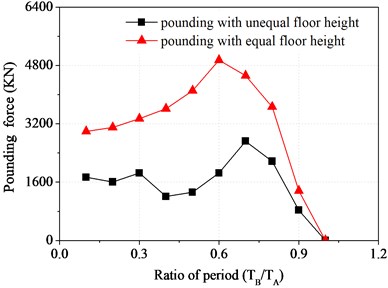
Fig. 9 shows that, with changing of period ratio, the displacement of interfloor pounding and floor pounding have the similar trends. In general, the influence of pounding on displacement of structure A (flexible one) is smaller than that of structure B (rigid one). The displacement of structure A increases with the increase of period ratio, it reaches the peak of 1.3 when period ratio is 0.6, and then reduces gradually. While the displacement curve of structure B has several peaks with the increase of period ratio, and the maximum peak value is more than 1.5. Besides, the time for the appearance of peak value has no obvious regular pattern. This is because structure A is more flexible than structure B, and essentially generates bigger displacement during earthquakes. But due to the limit of gap, the displacement does not increase significantly after pounding. Different from structure A, because the seismic displacement of structure B is essentially small, the limit to pounding displacement from gap is also small. Moreover, the appearance of peak values is influenced by many factors, and these factors will result in several peak values of pounding displacement.
Fig. 10 shows the peak values of pounding force for the top floor of structure B varying with period ratio under two working cases. It can be seen that the changing trends of pounding force peak values for interfloor pounding and floor pounding with the changing of period ratio are different. Besides the peak value of floor pounding is significantly larger than that of interfloor pounding, the time of the maximum peak appearance are not synchronous. The maximum peak value of pounding force for floor pounding occurs at the point of 0.7 for period ratio, which is the same as that of displacement, while that of interfloor pounding occurs at the point of 0.6 for period ratio. This is because pounding force for interfloor pounding is not only related to the natural vibration characteristics of main structure, but also related to that of substructure.
3.3. Influence of initial gap
The reason of pounding between adjacent structures is that the gap of them can not meet the vibration need. Accordingly, the initial gap size has important influence on pounding responses of adjacent structures. In order to study the law of influence of initial gap size on pounding response, assuming other parameters maintain unchanged, the changing curve between the peak value trends of displacement and force of top floor and the gap width are obtained and shown in Fig. 11 and Fig. 12.
Fig. 11Displacement ratio of top floor varying with the gap size
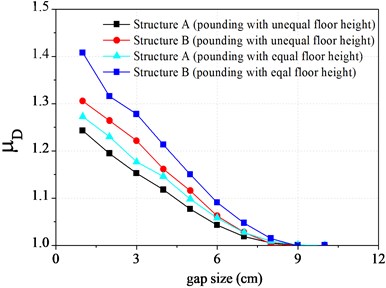
Fig. 12Pounding force of top floor varying with the gap size
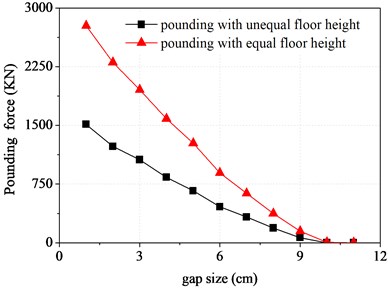
It can be seen from Fig. 11, whether structure A or structure B , and whether floor pounding or interfloor pounding, their displacement peak values all decrease with the increase of gap size. When the gap size reaches 9 cm, the displacement caused by pounding has become not very obvious already. In contrast, the displacement of interfloor pounding is bigger than that of floor pounding for corresponding individual. Pounding force curve of Fig. 12 shows similar rule as mentioned before. This is because the bigger the width of gap is, the higher the pounding frequency will be, and the smaller the pounding intensity will also be, which results in the smaller pounding responses.
3.4. Influence of staggering location
For the pounding of adjacent buildings for unequal floor height, which is interfloor pounding, is related to the stiffness of substructure, accordingly, the staggering location of pounding has important influence on pounding responses. In order to study the law of influence of staggering location on pounding responses, staggering location ratio is defined to represent the staggering location as follow:
where,, are the total heights of structure A and structure B respectively; is the floor height of the first floor for structure B.
Fig. 13Staggering location ration
Supposing that the other conditions maintain unchanged, the displacement and pounding force trends of top floor varying with the staggering location are obtained and shown in Fig. 14 and Fig. 15.
Fig. 14Displacement ratio of top floor varying with the staggering location
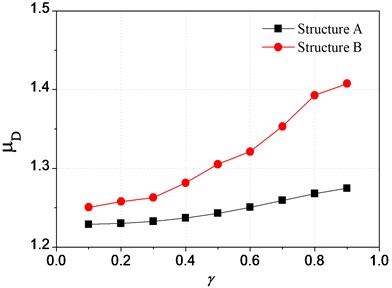
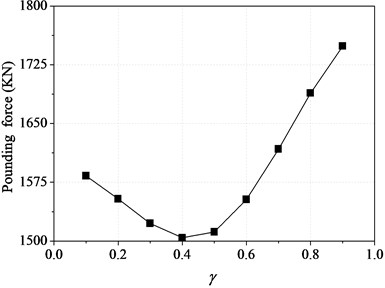
Fig. 15Pounding force of top floor varying with the staggering location
It can be seen from Fig. 14, both displacement peak values of structure A and structure B increase with the increase of . In comparison, the change trend of black curve (structure A) is gentler than that of red one (structure B). This is because, the bigger the value of is, which means the pounding point is closer to floor slab, the bigger the stiffness of substructure will be, and as a result, the bigger the pounding displacement of structure B will also be. However, as the pounding of structure A happens at the position of floor, the responses mainly depend on the stiffness and mass of main structure, hence, the influence on displacement of main structure caused by the change of the stiffness of substructure, i.e. change of , is correspondingly small.
It can be seen from Fig. 14, the peak values of pounding force decrease gently with the increase of . When is in the range of 0.4 to 0.5, the pounding force reaches its minimum value, after that, it increase significantly with the increase of . This is because, the peak value of pounding force mainly depends on stiffness of substructure, and when is in the range of 0.4 to 0.5, the stiffness of substructure approaches its minimum value, and accordingly, the pounding also approaches its minimum value.
4. Conclusions
The influence on main structure for interfloor pounding of adjacent buildings with unequal floor height is smaller than that for floor pounding of corresponding adjacent buildings with equal floor height, but it has a very large influence on the substructure (partial members). For the substructures are generally the members of baring vertical force, their failure can result in a significant influence on the safe of main structure. Therefore, the interfloor pounding for adjacent buildings of unequal floor height is more dangerous than that for adjacent buildings of equal floor height, sometimes. The responses of interfloor pounding for adjacent buildings of unequal floor height are related to the period ratio of structure and the initial gap size between adjacent buildings etc, and have the same (or similar) change law as those of corresponding floor pounding for equal floor height, yet, their responses are smaller. The interfloor pounding responses of adjacent buildings with unequal floor height are related to the staggering location of pounding point, the loser the location of pounding point approaches to floor, the larger the responses of pounding are.
References
-
Sadegh N., Farah N. A., Abdul Azizl, Hassan P. Earthquake induced pounding between adjacent buildings considering soil-structure interaction. Earthquake Engineering and Vibration, Vol. 11, Issue 3, 2012, p. 343-358.
-
Jeng V., Tzeng W. L. Assessment of seismic pounding hazard for Taipei City. Engineering Structures, Vol. 22, 2000, p. 459-460.
-
Rosenblueth E., Meli R. The 1985 earthquake: causes and effects in Mexico City. Concrete International, Vol. 8, Issue 5, 1986, p. 23-34.
-
Bertero V. V. Observations on structural pounding. International Conference Mexico Earthquakes, 1987, p. 264-278.
-
Wolf J. P., Skrikerud P. E. Mutual pounding of adjacent structures during earthquakes. Nuclear Engineering and Design, Vol. 57, 1980, p. 253-275.
-
Maison B. F., Kasai K. Dynamics of pounding when two building collide. Earthquake Engineering and Structural Dynamics, Vol. 21, 1992, p. 771-786.
-
Jankowski R. Earthquake-induced pounding between equal height buildings with substantially different dynamic properties. Engineering Structures, Vol. 30, 2008, p. 2818-2829.
-
Zou Lihua, Fang Leiqing, Huang Kai, Wang Liyuan Collision between adjacent buildings considering pile-soil-structure interaction (PSSI). Journal of Earthquake Engineering and Engineering Vibration, Vol. 31, Issue 5, 2011, p. 132-141.
-
Tubaldi E., Barbato M., Ghazizadeh S. A probabilistic performance-based risk assessment approach for seismic pounding with efficient application to linear systems. Structural Safety, Vol. 36-37, 2012, p. 14-22.
-
Zhao Jianwei, Zou Lihua, Fang Leiqing Seismic response analysis of base-isolated structures considering pounding of adjacent buildings. Journal of Vibration and Shock, Vol. 29, Issue 5, 2010, p. 215-219.
-
Zhai Changhai, Jiang Shan, Li Shuang, et al. Analysis of earthquake-induced pounding for two adjacent building structure. China Civil Engineering Journal, Vol. 45, Issue 2, 2012, p. 142-145.
-
Karayannis C. G., Favvata M. J. Earthquake-induced interaction between adjacent reinforced concrete structures with non-equal heights. Earthquake Engineering and Structural Dynamics, Vol. 34, 2005, p. 1-20.
-
Panayiotis C. Polycarpou, Petros Komodromos Earthquake-induced pounding of a seismically isolated building with adjacent structures. Engineering Structures, Vol. 32, 2010, p. 1937-1951.
-
Robert Jankowski Non-linear FEM analysis of pounding-involved response of buildings under non-uniform earthquake excitation. Engineering Structures, Vol. 37, 2012, p. 99-105.
-
Lin Jeng-Hsiang Separation distance to avoid seismic pounding of adjacent buildings. Earthquake Engineering and Structural Dynamics, Vol. 26, 1997, p. 395-403.
-
Bryan Stafford Smith, Alex Coull Tall Building Structures: Analysis and Design. John Wiley & Sons, Singapore, 1991.
-
Muthukumar S., DesRoches R. A. Hertz contact model with non-linear damping for pounding simulation. Earthquake Engineering Structural and Dynamics, Vol. 35, 2006, p. 816-819.
About this article
This work was financially supported by Chinese Housing and Urban-Rural Construction Ministry under Grant No. 2009-R4-8.
