Abstract
The paper states an analytical method for resolving the problem of scattering of multiple semi-cylindrical hills and the subsurface elastic cylindrical inclusion near the hills to the SH-wave by using of the complex function and moving coordinates. During the analysis, the whole model is divided into two parts, the part I consists of multiple circular domains which include multiple semi-cylindrical hills; the part II consists of multiple semi-cylindrical concaves and an elastic cylindrical inclusion. And then, the displacement solutions that satisfy the boundary conditions are respectively constructed in these two parts. The part I and II are matched up on the common boundary by moving coordinates according to the corresponding condition between the joint faces. At the same time, considering of the boundary condition of the elastic cylindrical inclusion, a set of infinite algebraic equations for resolving of the problem could be obtained. At last, according to the computational results, the paper indicates the influence of the distance between two hills and the buried depth of inclusion on the surface displacement amplitude.
1. Introduction
In earthquake engineering, it is important to study the effect of local topography on the ground motion. For the latest decades, many scholars engaged in the research of the influence of geometrical shape of the ground on the ground motion have obtained some significant achievements. The methods for solving such problem fall into the following two categories: analytical method and numerical method. As far as the analytical method is concerned, Trifunac presents the solution of scattering of SH-waves by a semi-cylindrical canyon by wave function expansion for the first time [1]. Afterwards, the studies on the problems of scattering of plane SH-waves by a canyon have been gradually developed and perfected [2-4]. While for the hill under SH wave, multiple reflection of the waves in the hill causes the problems of scattering by hill are much more complicated than by canyon. Using wave function expansion and division idea, scattering of SH wave by a semi-cylindrical hill was studied by Yuan Xiaoming in 1992 [5]; and then Liu et al. solves the same problem by complex function and conjunction method [6]. At the same time, the studies on dynamic analysis of shallow buried structures under SH wave achieve remarkable results [7-10]. In 2002, the problem of scattering of SH-wave by multiple circular cavities in half space was solved through the moving coordinates [11]. In 2006, leading work in analytical studies on the interaction of a hill and a subsurface cavity under SH wave was done by Wang [12]. And then, the scattering of SH-wave by isosceles triangular hill in half space and by scalene triangular hill on a right-angle field were studied successively [13-14]. All of these achievements effectively develop the studies of the irregular surface reflection. In this paper, an analytical method is provided for scattering of SH-wave by multiple semi-cylindrical hills above a subsurface elastic cylindrical inclusion, and the displacement variation of the hill’s surface is determined. Furthermore, the subsurface inclusion can be regarded as covered topography, and then the problem resolved in this paper will provide valuable reference for the further researching on partial topography.
During the solution, the whole solution domain is divided into two parts. The part I consists of multiple circular domains, each of them included the boundary of the hill, and all the rest can be considered as the part II. Firstly, a standing wave function is constructed in each circular domain, which satisfies the condition of stress free at the edge of the hill and the arbitrary at other part. In domain II, the scattered wave is constructed to satisfy the condition of stress free at the horizontal surface. Then, by moving coordinates, the two parts are conjoined on common boundaries, at the same time, considering the boundary condition at the edge of elastic cylindrical inclusion, the problem can be reduced to solving a series infinite linear algebraic equations.
2. Basic theories
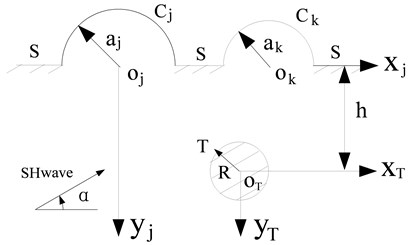
In Fig. 1, the model of an elastic half-space with a subsurface elastic cylindrical inclusion and (1, 2,…, ) semi-cylindrical hills is shown. To solve the scattering of SH wave by this model, we need to find a wave function which satisfies: 1) the stress free at the horizontal surface and the edge of hill (1, 2,…, ); 2) the displacement and stress continual at the edge of elastic cylindrical inclusion .
Fig. 1The model of multiple semi-cylindrical hills with a subsurface elastic cylindrical inclusion
3. Governing equations
In homogeneous, isotropic and continuous medium, the displacement caused by SH wave is normal to -plane and independent of , and the corresponding stresses are only exist in -plane. Introducing complex variables , , displacement satisfies the following equation:
where is the displacement function, the dependence relations of with time factor is (and will be omitted). , is the circular frequency of ; stands for the shear wave velocity of the medium. In the following discussion, , and , are mass density and shear modulus of medium and elastic inclusion respectively, .
In the polar coordinate system, the corresponding stresses can be written as:
4. Solution procedure
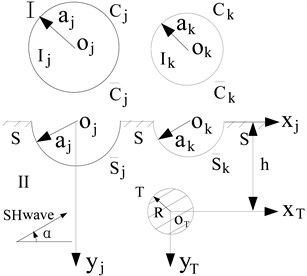
Using the division idea, the whole model is divided into two parts. As shown in Fig. 2, is a circular domain, including the boundary and (1, 2,…, ), and circular domains can be considered as part I. The part II consists of boundary , and . Obviously, and are the common boundaries of two parts, so the displacement and stress function should satisfy the continuity condition at the common boundary.
Fig. 2The division of the solution domain
1) Standing wave in domain (1, 2,…, ).
In circular domain , the disturbance excited by SH wave is a standing wave, which should satisfy the condition of stress free at the edge of the hill and arbitrary at the other parts. Therefore, in the complex plane which origin at the center of -th circular domain , the stresses corresponding to the standing wave should satisfy the following boundary condition [6]:
where is amplitude of incident wave, are unknown coefficients.
In complex plane (), the standing wave solution due to Eq. (3) can be expressed as:
The stress expression from Eq. (3) is:
in which:
2) Wave functions in domain II.
In domain II, the total wave field includes four parts: scattered wave from semi-cylindrical canyons, scattered wave from the elastic inclusion, incident wave and reflected wave . In order to satisfy the stress free condition at the horizontal surfaces , in the complex plane , the wave functions mentioned above can be expressed as:
where is the complex coordinates of the center of -th canyon in the complex plane , are unknown coefficients:
where is the complex coordinates of the elastic cylindrical inclusion center in the complex plane , and is the conjugate of complex variable :
By moving coordinates, in complex plane which origin at the center of elastic cylindrical inclusion , the expressions of wave functions in domain II (Eq. (7)-(10)) can be written as , , and :
in which , .
3) A standing wave in elastic inclusion .
In complex plane , the standing wave function in elastic inclusion can be given by:
According to Eq. (2), the expressions of stresses corresponding to the displacement functions (Eq. (7)-Eq. (15)) can be solved respectively.
4) Boundary conditions and determined equations.
As mentioned above, the boundary conditions of horizontal surface and the hills had been satisfied. Then domain I and domain II are assembled together in complex plane , and the boundary conditions of elastic cylindrical inclusion should be satisfied, which means that the displacements and radial stresses at the edge of inclusion should be continual. So all the conditions are:
Substituting the expressions of displacements and stresses into Eq. (16), and multiplying both sides of equations by and integrating over the interval , so a series infinite algebraic equations solving the unknown coefficients , , , can be obtained.
5. Surface displacement amplitude
In part II, the total wave field can be written as:
The dimensionless incident wave number is:
where is the wavelength of incident wave.
6. Example and interpretation of results
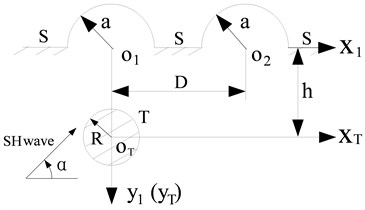
Calculation model is shown in Fig. 3. In the model, two hills have the same radius ; stands for the center distance of two hills; stands for the distance of horizontal surface to the inclusion center, is the radius of inclusion. Following discussions focus on the variation of left hill’s surface displacement amplitudes.
Fig. 3Calculation model
In order to discuss the influence of medium and inclusion shear modulus on the surface displacement, three groups ratio of dimensionless parameters are given: (1) , namely the shear modulus of medium is four times the value of the inclusion, that is to say, the medium is harder than the elastic inclusion; (2) , the medium and the inclusion have the same shear modulus, so the inclusion can be considered nonexistence; (3) , which means the medium is softer than the inclusion.
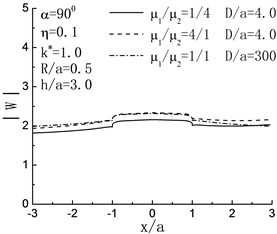
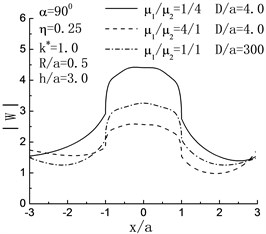
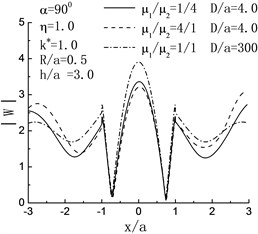
Fig. 4 illustrates the surface displacement amplitudes of left hill when , . For the case of incident angle , , , the influence of the right hill and the inclusion can be ignored, and the displacement distribution should agree with the case of single hill; and as shown in Fig. 4, when , , the variations of surface displacement absolutely identical to the results from the reference [2]. When , and , compared with the case of without the right hill, the displacement of the right side of the left hill peak shows decrease.
Fig. 4Variation of surface displacement of left hill with x/a when h/a=3.0
a)
b)
c)
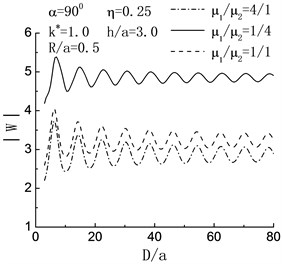
For the case of normal incidence and , in Fig. 5, it is obvious that the displacement amplitude of left hill peak tends to be periodicity with the increase of . When , the harder inclusion has remarkable magnifying influence on the displacement amplitudes of the hill peak, while the influence of softer inclusion is just the opposite. When , compared with the case of without inclusion, the existence of inclusion results in the decreased displacement amplitudes of the hill peak; and the softer the inclusion is, the more the decrease shows.
Fig. 5Variation of displacement amplitude of left hill peak with D/a when h/a=3.0
a)
b)
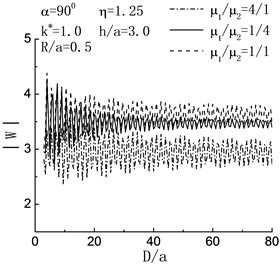
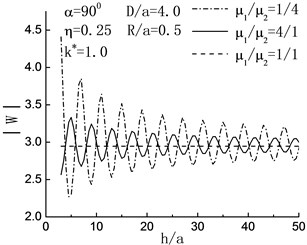
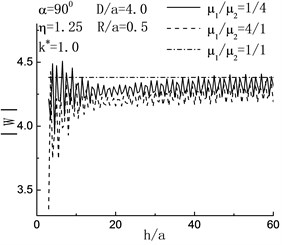
Fig. 6Variation of displacement amplitude of left hill peak with h/a when D/a=4.0
a)
b)
Fig. 6 shows the variation of displacement amplitude of left hill peak with the increase of . When the incident angle the degree of variability in displacement amplitude of left hill peak decreases with the increasing of embedded depth of inclusion, and tends to the status of no inclusion gradually. When , in the range of , the displacement amplitude of left hill peak decreases. It shows that the inclusion functions for decreasing the shake of ground.
7. Conclusions
1) The subsurface inclusion has notably amplified or reduced the influence on the displacement of the hill surface. And the concrete influence is dependent on the buried depth of inclusion and the ratio of shear modulus of inclusion to that of medium. But the hills will not be influenced by the inclusion when .
2) When the embedded depth of inclusion is fixed, the interaction between two hills displays the periodicity with the increase of the distance between the two hills. For the case of , the interaction can be ignored.
References
-
Trifunac M. D. Scattering of plane SH-waves by a semi-cylindrical canyon. Earthquake Engineering and Structure Dynamics, Vol. 2, 1973, p. 267-281.
-
Wang H. L., Trifunac M. D. Scattering of plane SH-waves by a semi-elliptical canyon. Earthquake Engineering and Structure Dynamics, Vol. 3, 1974, p. 158-169.
-
Liu D. K., Han F. Scattering of plane SH-waves by a cylindrical canyon of arbitrary shape in anisotropic media. Acta, Mechanics Sinica, Vol. 6, Issue 3, 1990, p. 256-266.
-
Nazaret D., Lee V. W., Liang J. W. Antiplane deformations around arbitrary-shaped canyons on a wedge-shape half space: moment method solutions. Earthquake Engineering and Engineering Vibration, Vol. 2, Issue 2, 2003, p. 281-287.
-
Yuan X. M., Men F. L. Scattering of plane SH-waves by a semi-cylindrical hill. Earthquake Engineering and Structure Dynamics, Vol. 21, 1992, p. 1091-1098.
-
Cui Z. G., Cao X. R., Liu D. K. Scattering of SH-wave by semi-cylindrical hill. Earthquake Engineering and Engineering Vibration, Vol. 18, Issue 1, 1998, p. 140-146.
-
Liu D. K., Lin H. Scattering of SH-waves by a shallow buried cylindrical cavity and the ground motion. Explosion and Shock Waves, Vol. 23, Issue 1, 2003, p. 6-12, (in Chinese).
-
Chen Z. G., Liu D. K. Dynamic response on a shallowly buried cavity of arbitrary shape impacted by vertical SH-wave. Earthquake Engineering and Engineering Vibration, Vol. 24, Issue 4, 2004, p. 32-36, (in Chinese).
-
Liang J. W., Luo H., Lee V. W. Diffraction of plane SH waves by a semi-circular cavity in half-space. Earthquake Science, Vol. 23, Issue 1, 2010, p. 5-12.
-
Liu Z. X., Liang J. W. Analytic solution for diffraction of plane SH waves by a circular alluvial valley in wedge-shaped space. Journal of Tianjin University, Vol. 43, Issue 7, 2010, p. 573-582, (in Chinese).
-
Wang G. Q., Liu D. K. Scattering of SH-wave by multiple circular cavities in half space. Earthquake Engineering and Engineering Vibration, Vol. 1, Issue 1, 2002, p. 36-44.
-
Liu D. K., Wang G. Q. Antiplane SH-deformation of a semi-cylindrical hill above a subsurface cavity. Acta Mechanica Sinica, Vol. 38, Issue 2, 2006, p. 209-218, (in Chinese).
-
Qiu F. Q., Liu D. K. Antiplane response of isosceles triangular hill to incident SH waves. Earthquake Engineering and Engineering Vibration, Vol. 4, Issue 1, 2005, p. 37-46.
-
Qi H., Guo J., Yang J. Scattering of SH-wave and ground motion induced by scalene triangular hill on a right-angle field. Journal of Vibration and Shock, Vol. 31, Issue 18, 2012, p. 157-162, (in Chinese).
