Abstract
The elastic and inelastic seismic demand of shear wall structures, with stiffness, strength and combined-stiffness-and-strength eccentricity, subjected to velocity pulse-like ground motions are investigated. Based on the axial load-bending moment interaction model and eight pulse-like ground motions, nonlinear dynamic time history analyses are conducted to single-story RC eccentric wall structures. The seismic demand is discussed in terms of the displacement, floor rotation and ductility, and the influence mechanism of different eccentricity types is revealed. The results show that the eccentric systems for pulse-like cases experience much higher elastic and inelastic seismic demand comparing to those for non-pulse-like cases. The axial compression ratio has certain effect on the inelastic seismic demand. The stiffness eccentricity is the key factor to the elastic seismic demand, while the strength eccentricity influences the inelastic seismic demand most. It is suggested that the strength eccentricity be added as a parameter in the inelastic analysis of eccentric structures, and the influence of axial load as well as velocity pulse-like effect of ground motions also be accounted in.
1. Introduction
Non uniform distribution of stiffness and strength in eccentric buildings causes the buildings to experience higher seismic demand and leads to increased damage, which has been observed during past earthquakes [1-3]. Rutenberg [4] and De Stefano [5] comprehensively reviewed numerous studies on the seismic behavior of eccentric structures in past decades. Since the early 1980’s numerous studies have been conducted to study the elastic and inelastic seismic demand of these structures [5-7]. Recently, more researches focus on investigating their inelastic seismic demand due to its complexity [8-10]. All these studies have reached agreement on the basic trend of the elastic seismic demand for eccentric structures, and some conclusions are adopted by seismic codes. However, there still exist controversial even opposite conclusions when structures are exited well into the inelastic range of responses. Sadek and Tso [11] introduced the concept of strength eccentricity and pointed out that the strength eccentricity is an appropriate indicator in the inelastic range. Later, Bufeja et al. [12] also demonstrated that the strength eccentricity has greater influence on the inelastic seismic demand than the stiffness eccentricity. However, it’s still controversial for the issue on the stiffness and strength eccentricity [13]. Most of the previous studies on eccentric structures were based on the simple uniaxial hysteretic model, which ignored the axial load-bending moment interaction [5-10]. Moreover, all these studies have not yet specially considered the velocity pulse-like effect of ground motions. Structural eccentricity and velocity pulse-like ground motion are two disadvantageous design conditions, and their combined influence on the structural elastic and inelastic seismic demand needs to be further studied.
Past experiences show that velocity pulse-like effect of ground motions have significant influence on structural seismic responses. Previous studies [14-16] also demonstrated that structures subjected to pulse-like ground motions have larger drift and strength demands compared with structures subjected to common earthquake actions. As a result, most of the current seismic codes, such as EC8 [17], AS/NZS standard [18], Chinese seismic code [19], and etc., came to consider this disadvantageous effect by employing an amplification factor for earthquake load. However, all these codes didn’t distinguish the generic symmetric structures from unfavorable eccentric structures. In addition, numerical simulation studies and experimental tests simultaneously accounting for the effects of structural eccentricity and velocity pulse-like effect are rare, although independent research is adequate.
The objective of this work is to comparatively study the combined influence of velocity pulse-like effect of ground motions and structural eccentricity on the elastic and inelastic seismic demand for eccentric structures through nonlinear time history analysis method. Three eccentricity types, including stiffness, strength, and combined stiffness-and-strength eccentricity, are introduced. The influence mechanism of these eccentricities and influence of the axial load on elastic and inelastic seismic demand are revealed. The elastic seismic demand is in terms of the displacement of edge walls and floor rotation, while inelastic seismic demand considers the ductility in addition. The conclusions can provide a reference in seismic codes for considering the combined influence of pulse-like ground motion and structural eccentricity.
2. Structural model and input ground motions
2.1. Symmetric model
Reference symmetric structures, which are simplified by employing several wall elements like many famous researches did [8, 9], are first designed and the basic information is shown in Fig 1 (0). The analytical models are established by a structural nonlinear analysis program CANNY [20]. The constitutive model for the concrete and steel material are CS4 and SR4, respectively. The axial and shear hysteretic model for the wall element are AS2 model and CA7 model, ignoring the out plane resistance like many studies assumed. The default hysteretic parameters recommended by the program are selected [20]. For resisting the in plane bending, AM3 model are employed to consider the axial load-bending moment interaction (Fig. 2). Comparing to the simple uniaxial hysteretic models widely used for eccentric structures by previous studies, AM3 model can consider the influence of varying axial load on the moment. Although AM3 model is simpler than the well known fiber model which can automatically consider the axial load-bending moment interaction, it provides a effective way for calculating the ductility demand as it can directly defines the yield point while the fiber model cannot. The more details of these hysteretic models are available in reference [20].
Fig. 1Schematic diagram of the asymmetric and eccentric structure
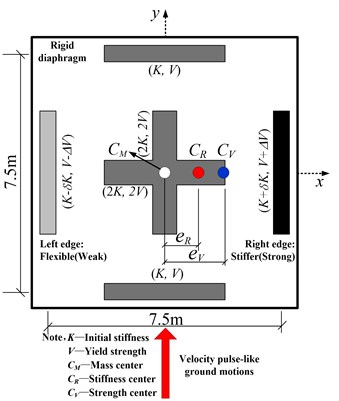
a) Plan
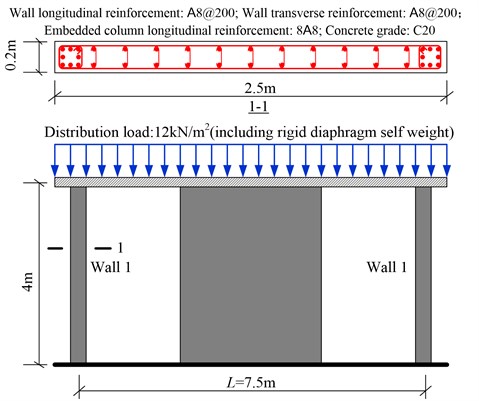
b) Elevation
Fig. 2Principle of AM3 model
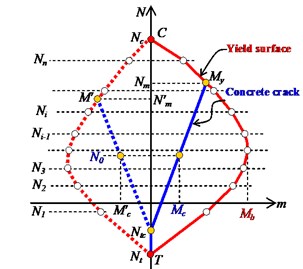
a) Axial load-bending moment interaction
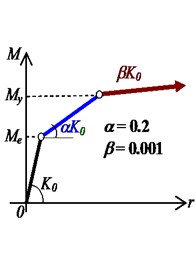
b) Tri-linear skeleton curve
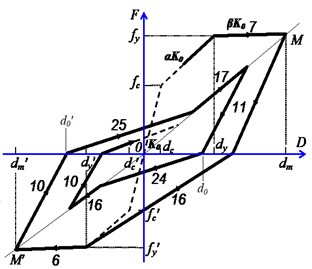
c) Takeda hysteretic model
2.2. Eccentric model
Three types of eccentricities, including stiffness, strength and combined stiffness-and-strength eccentricity, are introduced by changing the stiffness and strength distribution of edge walls, as shown in Fig. 1. The right wall with increased stiffness (strength) is defined as stiffer (strong) edge, and the left wall with reduced stiffness (strength) is the flexible (weak) edge. Namely, these eccentricities are realized by changing the stiffness factor and strength factor in Fig. 1, and can be listed as the following cases.
1) Stiffness eccentricity type: 0, ; 0, .
2) Strength eccentricity type: 0, ; 0, .
3) Combined stiffness-and-strength eccentricity type: 0, ; 0, ,
where is the offset of stiffness center from mass center , is the offset of strength center from mass center, and is the structural length along axis, respectively. and denote the stiffness and strength eccentricity ratio, which can be defined as [11, 12]:
where and are the th wall stiffness and yield strength along axis, and is the offset of the th wall from the mass center , respectively. Note that the total structural stiffness and strength along axis are unchanged to make effective comparison. In addition, the combined eccentricity is limited to the case with equal stiffness eccentricity and strength eccentricity, due to the impossibility to deal with infinite combination cases.
2.3. Input ground motions
The input ground motions are listed in Table 1 and the pulse indicator is denoted as:
where is a predictor of the likelihood that a given record is pulse-like, “” is the ratio of the peak ground velocity () of the residual earthquake record to the original record’s , and “” is the ratio of the residual record’s energy to the original record’s energy, respectively [15]. takes values between 0 and 1, with high values providing a strong indication that the ground motion is pulse-like. Records with scores above 0.85 and below 0.15 are classified as intense pulses and non-pulses, respectively. In the present study, takes values not less than 0.97, which represents the intense velocity pulse effects.
Table 1List of pulse-like ground motions used in the present study
No. | Earthquake event | Station | PGA / (cm/s2) | PGV / (cm/s) | ||
Q1 | Landers | Barstow | 7.3 | 696.3 | 30.4 | 1.00 |
Q2 | San Fernando | Pacoima Dam (upper left) | 6.6 | 1407.7 | 116.5 | 0.97 |
Q3 | Imperial Valley-6 | El Centro Array #7 | 6.5 | 453.2 | 108.8 | 1.00 |
Q4 | Imperial Valley-6 | EC County Center FF | 6.5 | 167.7 | 54.5 | 1.00 |
Q5 | Imperial Valley-6 | EC Meloland Overpass FF | 6.5 | 263.3 | 115.0 | 1.00 |
Q6 | Northridge-1 | Pacoima Dam (upper left) | 6.7 | 1349.7 | 107.1 | 1.00 |
Q7 | Northridge-1 | Newhall – W Pico Canyon Rd | 6.7 | 417.1 | 87.8 | 1.00 |
Q8 | Chi-Chi, Taiwan | CHY101 | 7.6 | 442.6 | 85.4 | 1.00 |
3. Influence mechanism of eccentricity and axial load
3.1. Influence mechanism of stiffness and strength eccentricity
Most previous studies focus on the change trend of the seismic demand for stiffness or strength eccentric structures, while the influence mechanism of these different types of eccentricities is not well understood [5-10]. The influence mechanism is revealed based on the simplified bi-linear hysteretic model in the present study. For stiffness eccentric systems in Fig. 3(a), the three skeleton curves represent the force-deformation relationship of the stiffer edge, reference central wall and flexible edge, respectively. They are with the same yield strength but differ in stiffness both in the elastic and inelastic range, which implies that the stiffness eccentricity can influence both the elastic and inelastic seismic demand. For strength eccentric systems in Fig. 3(b), the three skeleton curves represent the force-deformation relationship of the strong edge, reference central wall and weak edge, respectively. Their initial elastic stiffness is equal, which demonstrates that the elastic seismic demand is not influenced by the strength eccentricity. However, it goes different when structures are excited well into the inelastic range. Namely, the inelastic seismic demand will be influenced due to different strength distribution of the three elements along the ground motion direction. Therefore, the elastic seismic demand is influenced by the stiffness eccentricity while the inelastic seismic demand is influenced by both the stiffness eccentricity and strength eccentricity. Further numerical analysis should still be conducted to find out which is a much better and sensitive parameter for controlling the inelastic seismic response for eccentric structures.
Fig. 3Influence mechanism of the eccentricity
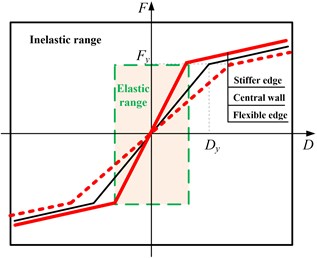
a) Stiffness eccentricity
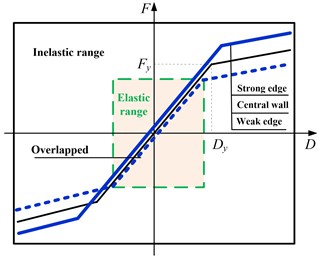
b) Strength eccentricity
3.2. Influence mechanism of axial load
Fig 4 shows the influence of axial load on the elastic and inelastic seismic demand of a reference symmetric structure, which is compared by the ratio of seismic demand with axial compression ratio (0) to that with 0 (i.e., without considering the axial load). “” and “” denote the maximum moment and displacement demand, and the subscript “” and “” denote the elastic and inelastic analysis cases, respectively. The axial compression ratio is varied from 0 to 0.06 considering the range of actual axial load for single-story RC wall structure.
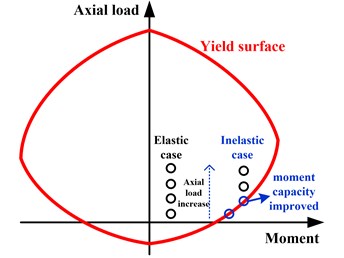
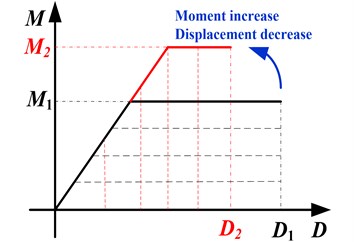
For elastic case with of 0.05 ( is short for peak ground acceleration, and its unit “” is gravity acceleration), the moment and displacement ratios hold a horizontal line with the change of axial compression ratios, which implies that the axial load has no influence on the elastic seismic demand. For inelastic case (0.7), the moment increases and the displacement decreases with the increment of axial load when is less than 0.03, while they will not change when is larger than 0.03. It can be explained in Fig. 5(a) by that the moment capacity will be improved with increasing axial load due to the axial load-bending moment interaction. This increment of moment capacity makes the structure experience larger moment demand and finally leads to decreased displacement demand, which can be explained by the equal energy theory in Fig. 5(b). However, when is beyond 0.03, it is found that the structure goes into elastic response. As a result, the moment and displacement will not change as the structure will behave elastically even at larger PGA of 0.7. Thus, although the axial load have no influence on the elastic seismic demand, it do influence the inelastic seismic demand. Comparing to most previous studies on eccentric structures by considering the simplified uniaxial hysteretic model with only resisting the horizontal seismic load, this study is much practical as the axial load-bending moment interaction is considered.
Fig. 4Influence of axial compression ratio on elastic and inelastic seismic demand
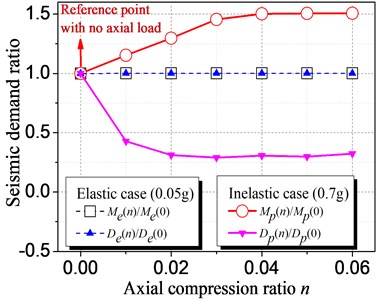
Fig. 5Influence mechanism of axial load
a) Axial load-moment interaction
b) Equal energy theory
4. Analysis results and discussion
The elastic and inelastic seismic demand of structures with stiffness, strength and combined eccentricity are compared, in terms of the displacement (), floor rotation () and element ductility (). The elastic and inelastic analysis is well conducted by scaling the peak ground acceleration () to be 0.05 and 0.7 respectively, ensuring all structural models maintain elastic at of 0.05 and go well into inelastic response at of 0.7. Only the stiffer (strong) and flexible (weak) edge are discussed as they are the key members to controlling the structural response compared to the central wall. Except for the additional notes, all the following results discussed is averaged over the eight pulse-like ground motion cases as the change trend for individual cases are similar. The stiffness, strength and combined eccentricity are abbreviated as KE, SE, and CE for convenience. The notations of “” and “” denote the reference symmetric model and the eccentric model, respectively.
Totally, elastic and inelastic time history analyses are performed for the following permutations: eight pulse-like ground motion records; two structural types of eccentric and reference symmetric models; three eccentricity types of KE, SE and CE; six eccentricity ratios of 0.05, 0.1, 0.15, 0.2, 0.25 and 0.3, which represent small, median and large eccentricity levels, respectively; two PGAs of 0.05 and 0.7, denoting the elastic and inelastic analysis cases.
4.1. Influence of different eccentricities on elastic seismic demand
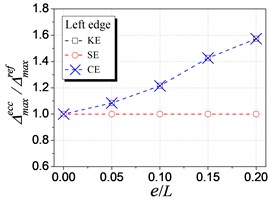
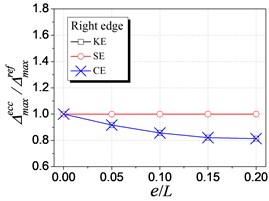
Fig. 6 shows the influence of KE, SE and CE on the elastic seismic demand, in terms of the displacement and floor rotation. As shown in the figure, both the displacement and floor rotation ratio are influenced by KE and CE but are not influenced by SE, which validates the mechanism in Fig. 3. The influence curve of CE overlaps with that of SE because it is the combination of the other two and SE have no influence in elastic range. With the increment of KE ratio, the left (flexible) edge displacement increases, the right (stiffer) edge displacement decreases, and the floor rotation increases. These elastic seismic responses are observed to vary linearly. Thus, it is reasonable to adopt the stiffness eccentricity as an indicator for controlling the elastic response for eccentric structures, as the current seismic provisioned.
Fig. 6Influence of different eccentricities on elastic seismic demand
a) Left edge displacement
b) Right edge displacement
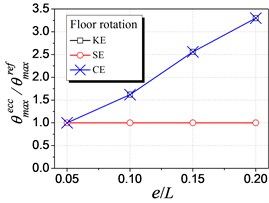
c) Floor rotation
4.2. Influence of different eccentricities on inelastic seismic demand
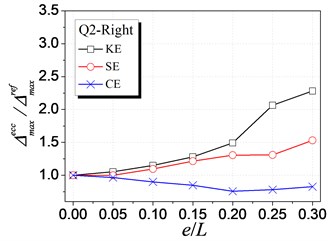
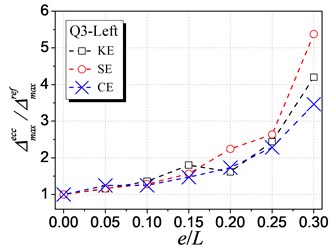
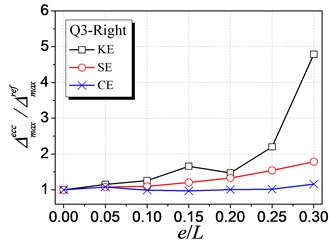
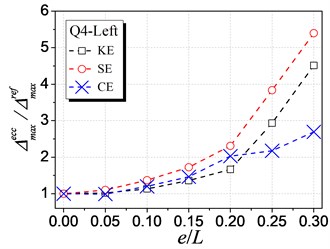
Fig. 7 shows the influence of KE, SE and CE on the inelastic displacement demand. The analysis results are only presented for cases under earthquake excitations from Q1 to Q4 shown in Table 1, as cases from Q5 to Q8 have the similar trends. The following trends can be observed from Fig. 7:
(1) For the left edge, the inelastic displacement demand increases with the increment of all the three types of eccentricities. Generally, the influence of SE is the largest, KE least, and CE medium.
(2) For the right edge, it becomes different that the influence of KE is largest. Meanwhile, the inelastic displacement may decrease with increasing CE, which provides a method for reducing the inelastic seismic demand of eccentric structures by controlling the balance position between the stiffness center and the strength center.
Fig. 7Influence of different types of eccentricity on inelastic seismic displacement demand
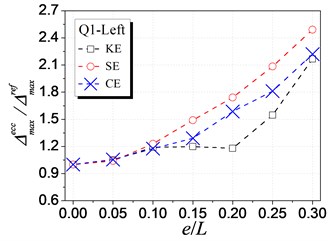
a) Q1 case-Left edge
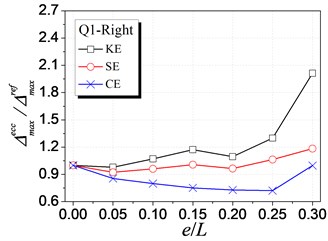
b) Q1 case-Right edge
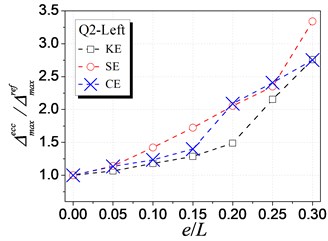
c) Q2 case-Left edge
d) Q2 case-Right edge
e) Q3 case-Left edge
f) Q3 case-Right edge
g) Q4 case-Left edge
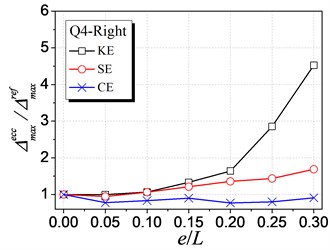
h) Q4 case-Right edge
(3) By comparing the inelastic displacement of the left edge to that of the right edge, it can be observed that the left edge displacement is larger than the right one for an identical eccentricity ratio. It demonstrates that the left (flexible or weak) side wall is the most unfavorable element influencing the inelastic seismic behavior. Thus, the strength eccentricity (SE) is the main factor to control the inelastic displacement of the whole eccentric structures as SE is the most apparent factor influencing the unfavorable left edge.
Fig. 8 shows the influence of different types of eccentricities on the inelastic floor rotation demand. The inelastic floor rotation with of 0.05 is selected as a comparing reference, for no floor rotation occurs in the case of 0 under unidirectional ground motion (i.e., the symmetric structure with uniform stiffness and strength distribution along the ground motion direction). As shown in Fig. 8, the inelastic floor rotation increases with the increment of all of the three eccentricity types. The influence of SE is larger than that of KE. However, the influence of CE is much close to that of SE rather than the superposition of KE and SE, due to the complicated inelastic behavior.
Fig. 8Influence of different eccentricities on inelastic rotation
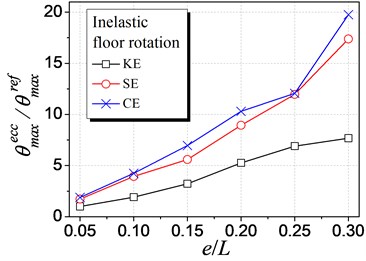
Fig. 9 illustrates the influence of different eccentricity types on the element ductility demand. As shown in Fig. 9(a), SE influences the ductility of left (weak) edge most, with a rapid nonlinear increasing trend. It is different for KE case that the ductility of left (flexible) edge decreases with increasing KE, and the change trend is much smaller than SE case. The influence of CE is similar with SE case. However, its increasing trend is much smaller owing to that CE is the combination of the other two and KE reduced the ductility demand. In Fig. 9(b), it is found that KE influences the right (stiffer) edge ductility most. In addition, the ductility increases with the increment of KE and decreases with the increment of SE or CE. Comparing Fig. 9(a) to Fig. 9(b), the left edge ductility is much larger than the right edge ductility, which implies that the left edge is the most unfavorable element. As a result, SE, influencing the unfavorable left edge most, is the predominated factor to the whole eccentric structure. Meanwhile, it is also suggested that the strength eccentricity be considered in the inelastic analysis for eccentric structures.
Fig. 9Influence of different eccentricities on ductility demand
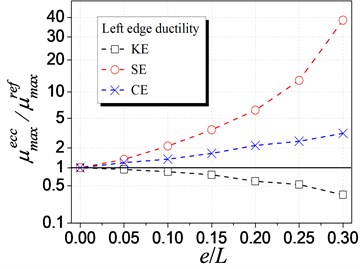
a) Left edge
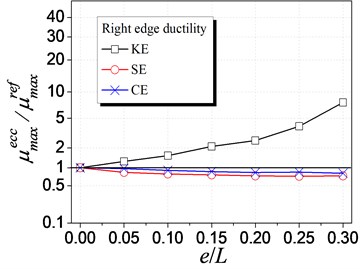
b) Right edge
4.3. Influence of velocity pulse-like effect of ground motions
To well understand the velocity pulse-like effect, a non-pulse-like ground motion ( 0.15) corresponding to Q1 (the pulse-like ground motion in Table 1) was generated using Baker’s method and excited to eccentric structures [15]. The elastic and inelastic seismic demand are compared between the pulse-like and non-pulse-like ground motion cases, as presented in Fig. 10. In these figures, “” denotes the seismic demand, the subscript “” and “” denote the elastic and inelastic analysis cases, and the superscript “” and “” denotes the pulse-like and non-pulse-like ground motion cases, respectively.
Fig. 10(a) compares the elastic seismic demand of eccentric structures between the pulse-like and the non-pulse-like ground motion cases, in terms of the elastic displacement and floor rotation. The stiffness eccentricity is employed as it is proved the main factor to elastic behavior (discussed in Section 4.1). The elastic displacement and floor rotation of the pulse-like case is larger than that of the non-pulse-like case by 10 % and 9 %, respectively. These increment do not change with the increment of the eccentricity ratio, which demonstrates that the pulse-like effect of ground motions and structural eccentricity have no coupling influence in elastic range and can be seen as individual factors in analyzing the structural elastic demand.
Fig. 10(b) compares the inelastic seismic demand of eccentric structures between the pulse-like and the non-pulse-like ground motion cases, in terms of the inelastic displacement, floor rotation, and ductility demand. Differing from Fig. 10(a), the strength eccentricity is employed as it is the predominated factor to inelastic behavior (discussed in Section 4.2). When the eccentricity ratios are less than 0.2 (i.e., the small and medium eccentricity range), both the inelastic displacement and floor rotation increase with the increasing eccentricity ratio, with a maximum increment of 30 % and 70 %, respectively. However, there exists no apparent trend for inelastic rotation, and displacement as well as ductility beyond the eccentricity ratio of 0.2, which needs to be further studied due to the strong nonlinear behavior. Thus, the pulse-like effect of ground motion can generally increase the inelastic displacement and ductility. In addition, the velocity pulse-like effect and structural eccentricity have coupling influence and can further aggravate the structural inelastic seismic demand, which is totally different from the elastic analysis cases in Fig. 10(a).
Fig. 10Influence of velocity pulse-like effect of ground motions on seismic demand
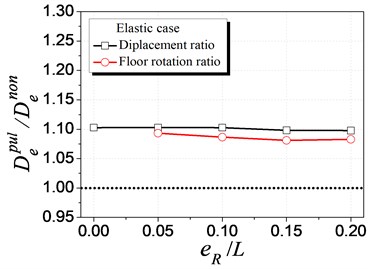
a) Elastic case
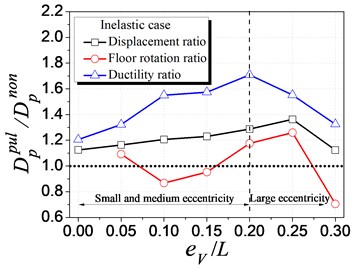
b) Inelastic case
4.4. Code provision for velocity pulse-like effect
Most of the current seismic codes, such as EC8 [17], AS/NZS standard [18], Chinese seismic code [19], and etc., came to consider the unfavorable pulse-like effect of near fault ground motions by employing an amplification factor, due to its destructiveness on structures. For instance, the AS/NZS standard [18] considered this effect by multiplying a near fault factor (, ), which is a function of period and the near fault distance ; Chinese seismic code [19] also adopted an amplification factor larger than 1.25 to ensure the safety of structures under near fault pulse-like ground motions. However, these amplification factors were based on engineering experiences and all these codes didn’t distinguish the generic symmetric structures and unfavorable eccentric structures. As illustrated in Section 4.3, the pulse-like effect and structural eccentricity can be considered as individual factors in the elastic range. In such cases, the current provision is reasonable as there are individual specifications for these two advantage conditions. However, these individual specifications may be insufficient in the inelastic range, owing to that the pulse-like effect and eccentricity have coupling influence and may cause larger inelastic response. Thus, further study should be conducted to evaluate on whether the current individual amplification factor in seismic codes is enough for considering the coupling influence of these two disadvantageous design conditions.
5. Conclusions
The elastic and inelastic seismic demand of single-story RC wall structures, with stiffness, strength, and combined eccentricity, subjected to velocity pulse-like ground motions are investigated. The following conclusions can be drawn from the results of this study:
(1) Eccentric wall structures subjected to velocity pulse-like ground motions will experience larger elastic and inelastic seismic demand comparing to non-pulse-like cases. The pulse-like effect and structural eccentricity can be considered as individual factors in elastic range, while they have coupling influence in the inelastic range. It needs to be further studied whether the individual amplification factor provisioned in current seismic codes is enough for considering this coupling influence. It is also suggested that the pule-like and non-pulse-like effect be distinguished in the inelastic analysis of eccentric structures.
(2) In elastic range, the axial load has no influence on the seismic demand such as elastic moment and displacement. However, it will influence the inelastic seismic demand due to the axial load-bending moment interaction. Most previous researches on eccentric structures, which employed the simple uniaxial hysteretic model and didn’t consider axial load-bending moment interaction, are not reasonable and need to be revisited.
(3) The main factor controlling the elastic seismic demand is stiffness eccentricity (KE), while the predominated factor is strength eccentricity (SE) in inelastic range. Specifically, with the increment of KE, the inelastic displacement of both the flexible and stiffer edge increase, while the flexible edge ductility decreases and the stiffer side ductility increases. For strength eccentric structures, the inelastic displacement of both edges increase with the increment of SE, but with a larger influence than KE cases. In addition, the weak edge ductility increases while the strong edge ductility decreases with the increment of SE, which is opposite from KE cases. It is suggested that the strength eccentricity be added as a basic parameter in the inelastic analysis of eccentric structures.
Although the present study is based on the single-story structural model, it can provide useful information and qualitative conclusion for multistory eccentric structures as illustrated in previous studies [4, 12]. Future study needs to extend to frame, frame-shear wall and shear wall structures with multistory eccentricity. Meanwhile, the complicated conditions such as bidirectional eccentricity and multi-dimensional earthquake excitations need to be considered in future work.
References
-
Chandler A. M. Building damage in Mexico City earthquake. Nature, Vol. 320, 1986, p. 497-501.
-
Goyal A., Sinha R., Chaudhari M., et al. Damage to R/C structures in urban areas of ahmedabad and bhuj, EERI preliminary reconnaissance report on earthquake in Gujrat, India. Earthquake Engineering Research Institute, Oakland, California, USA, 2001.
-
Rutenberg A. Nonlinear response of asymmetric building structures and seismic codes: a state of the art review. Proceedings of the Nonlinear Seismic Analysis and Design of Reinforced Concrete Buildings, Bled, Slovenia, 2004.
-
De Stefano M., Pintucchi B. A review of research on seismic behaviour of irregular building structures since 2002. Bulletin of Earthquake Engineering, Vol. 6, Issue 2, 2008, p. 285-308.
-
Kan C. L., Chopra A. K. Torsional coupling and earthquake response of simple elastic and inelastic systems. Journal of the Structural Division, Vol. 107, Issue 8, 1981, p. 1569-1588.
-
Tso W. K., Zhu T. J. Design of torsionally unbalanced structural systems based on code provisions I: Ductility demand. Earthquake Engineering & Structural Dynamics, Vol. 21, Issue 7, 1992, p. 609-627.
-
Dutta S. C., Das P. K. Inelastic seismic response of code-designed reinforced concrete asymmetric buildings with strength degradation. Engineering Structures, Vol. 24, Issue 10, 2002, p. 1295-1314.
-
Dutta S. C., Roy R. Seismic demand of low-rise multistory systems with general asymmetry. Journal of Engineering Mechanics, Vol. 138, Issue 1, 2012, p. 1-11.
-
Roy R., Chakroborty S. Seismic demand of plan-asymmetric structures: a revisit. Earthquake Engineering and Engineering Vibration, Vol. 12, Issue 1, 2013, p. 99-117.
-
Bosco M., Marino E. M., Rossi P. P. An analytical method for the evaluation of the in-plan irregularity of non-regularly asymmetric buildings. Bulletin of Earthquake Engineering, 2013, p. 1-23.
-
Sadek A. W., Tso W. K. Strength eccentricity concept for inelastic analysis of asymmetrical structures. Engineering Structures, Vol. 11, Issue 3, 1989, p. 189-194.
-
Bugeja M. N., Thambiratnam D. P., Brameld G. H. The influence of stiffness and strength eccentricities on the inelastic earthquake response of asymmetric structures. Engineering Structures, Vol. 21, Issue 9, 1999, p. 856-863.
-
Wang D., Lu X. L. Progress in study on inelastic torsional seismic response of asymmetric buildings. Journal of Earthquake Engineering and Engineering Vibration, Vol. 30, Issue 2, 2010, p. 51-58.
-
Bertero V. V., Mahin S. A., Herrera R. A. Aseismic design implication of near-fault San Fernando earthquake records. Earthquake Engineering and Structural Dynamics, Vol. 6, Issue 1, 1978, p. 31-42.
-
Baker J. W. Quantitative classification of near-fault ground motions using wavelet analysis. Bulletin of the Seismological Society of America, Vol. 97, Issue 5, 2007, p. 1486-1501.
-
Zhou J., Chen K. L., Huang Liang Effects of scaled pulse-like ground motion records on nonlinear structural displacement response. Journal of Vibration and Shock, Vol. 30, Issue 2, 2011, p. 104-109.
-
Eurocode 8. Design of structures for earthquake resistance – general rules, seismic actions and rules for buildings. CEN, Brussels, 1998-1, 2005.
-
AS/NZS 1170.4. Structural design actions – Part 4 earthquake actions, general design requirement and loading on structures. Australian, New Zealand, 2004.
-
GB50011-2010. Code for seismic design of buildings. China Architecture Industry Press, Beijing, 2010.
-
Li K. N. Three-dimensional nonlinear static/dynamic structural analysis computer program-users’ manual and data-input manual of CANNY. Vancouver, 2010.
About this article
The authors acknowledge the financial support by National Natural Science Foundation of China (50878087), State Key Lab of Subtropical Building Science, South China University of Technology (2014ZA06), and Natural Science Foundation of Hunan Province of China (12JJ6047).
